Linear Regression
-
A statistical method to study relationship between and
- : covariate / predictor variable / independent variable / feature
- : response / dependent variable
- output이 deterministic하게 나오는 것이 아니라, 분포에서 나온다.
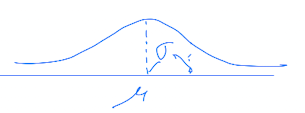 ➡️ instead of
➡️ instead of
-
Training data (, ), (, ), ..., (, )
-
Find a model that approximate
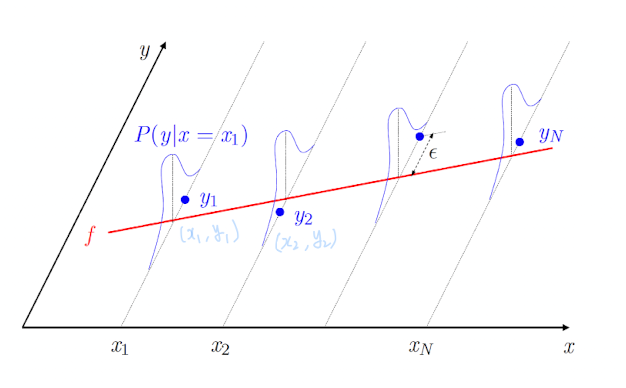
-
Classification은 catergorical 값을 예측하는 것이 목적이있는데,
Regression은 real-valued(실수값)에 대한 값을 예측하는 것이 목적이다.
Simple vs Multiple
- : Simple Linear Regression
- : Multiple Linear Regression
➡️ We discuss Simple LR from a learning perspective
Parameter Estimation for LR
-
Least squares
- Ordinary Least Squares(OLS)
: prediction
: target

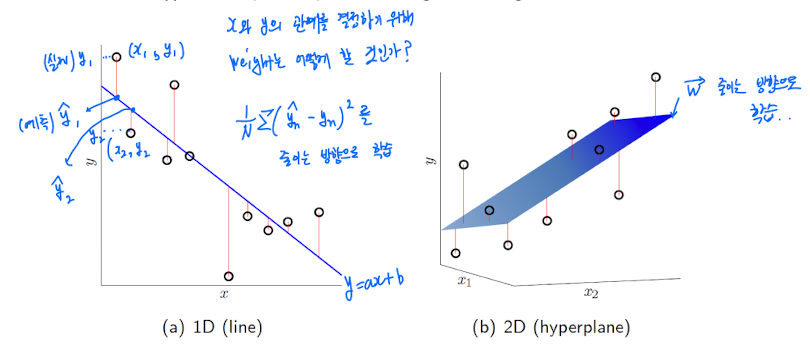
- Ordinary Least Squares(OLS)
-
Maximum likelihood
- Ridge / Lasso Regression
- Least Absolute Deviation Regression
-
Other Techniques
- Bayesian LR, Principal Componenet Regression
Example : Credit Approval Revisited
-
In Binary Classification, Approve credit or not?
-
In Regression... instead of making a binary decision,
Set a credit limit(= real number) for each customer

-
Regression에서는 output이 deterministic function을 통해 나오는 것이 아니라,
distribution을 통해 나온다고 했으니까
credit limit을 정해주는 담당자가 한 명 있는 것이 아니라,
담당자가 여러명 있다는 것이다.
➡️ 담당자가 한 명이라면, deterministic한 값을 내려줄 것이지만
여러명이라면, 각각 credit limit이 조금씩 다르니까 어떠한 Distribution이 만들어질 것이다.
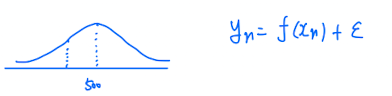
따라서
Classification의 경우, Learning의 목표는 unknown target function 를 찾는 것.
Regression의 경우, Learning의 목표는 unknown distribution 를 찾는 것.
➡️ 우리의 hypothesis 와 target 의 Sum of Squared Error를 최소화하는 방향으로 학습을 시킨다.
Linear Regression Algorithm
Definition of E_{in}
-
궁극적인 목표는 를 최소화하는 hypothesis 를 찾는 것이었지만
는 몰라서 을 구할 수 없기 때문에
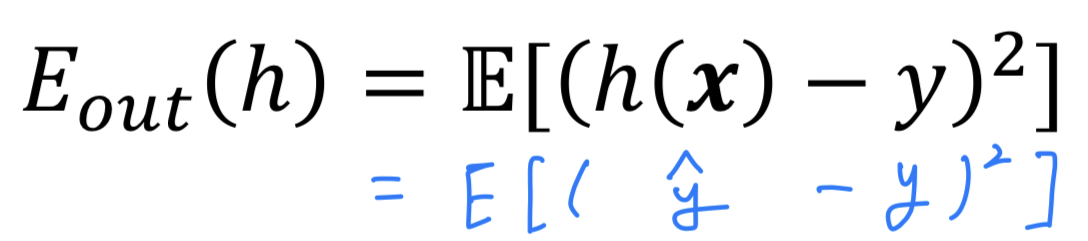
다음의 방법을 통해 결국 를 minimize했었다.

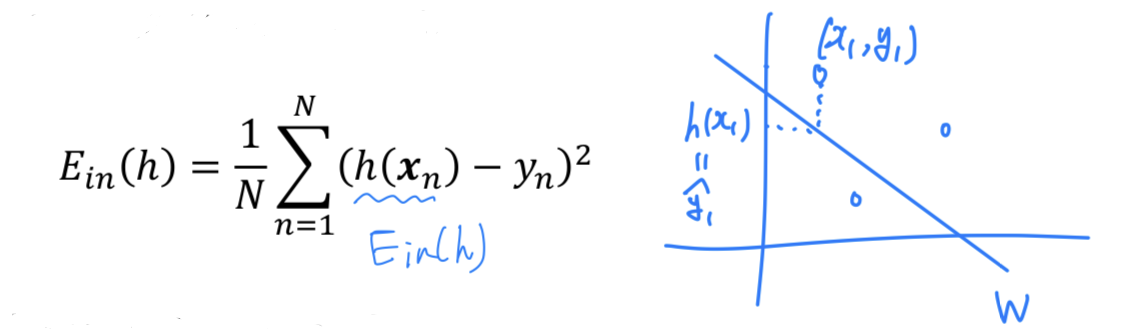
-
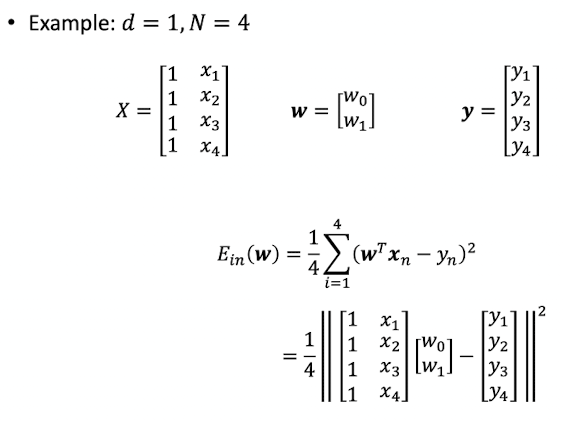
In Linear Regression, takes the form of
: also called signal
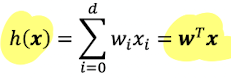
data
- N개의 data가 있다고 가정.
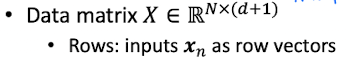

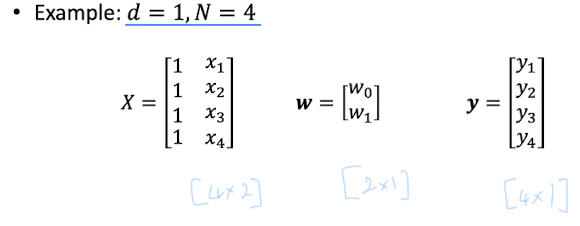
How to find E_in
-
In-sample error is a function of and data
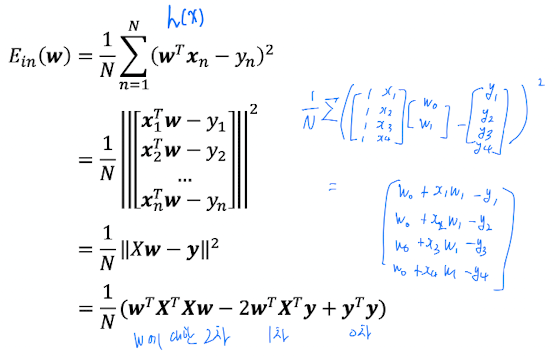
-
Optimal Weight를 어떻게 찾을 것인가?
➡️ 미분을 통해 최솟값을 찾는다.

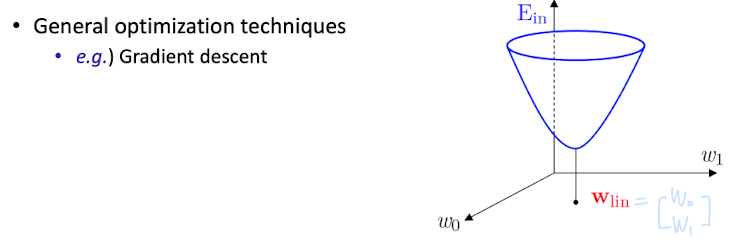
- 이전에 했던 PLA, Pocket Algorithm에 대한 Error들은
연산(step function)이 포함되어 있어서
미분이 불가능했었다.
- 이전에 했던 PLA, Pocket Algorithm에 대한 Error들은
Minimization of E_in(w)
-
따라서 에 대해 미분하여 0을 만드는 가 바로 Optimal Weight가 될 것이다.
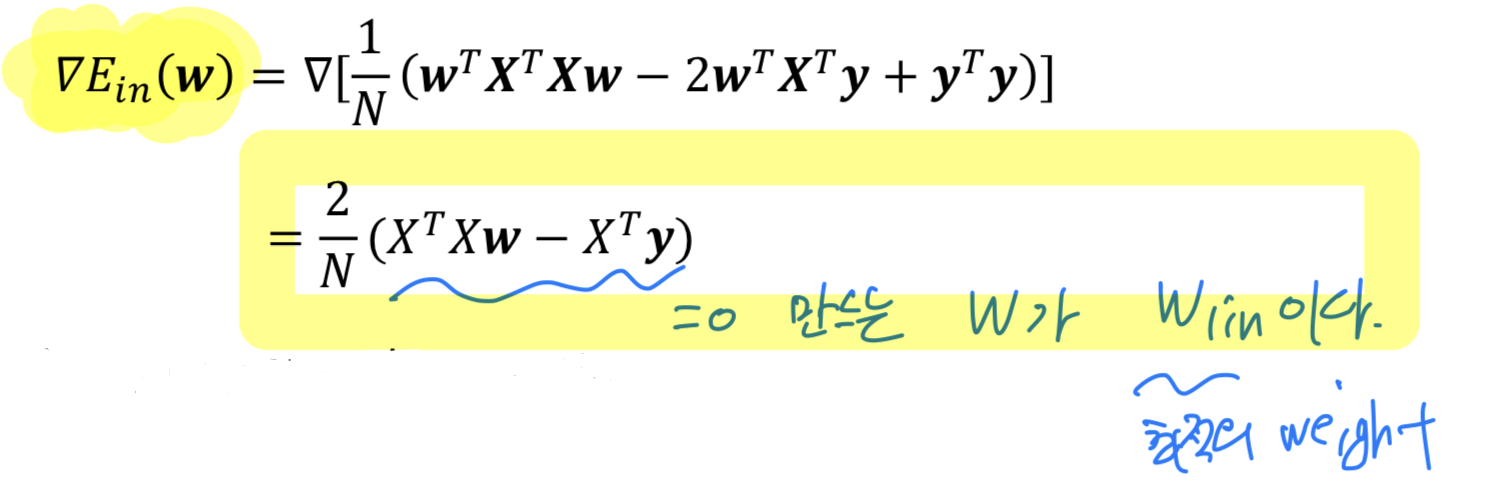
-
위에 를 미분한 식에서
을 만족하는 를 찾아야 한다.
➡️
➡️ ,
( : Psuedo-inverse of )
Example : Oxygen and Hydrocarbon levels
- Example
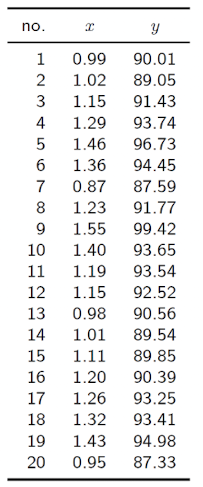

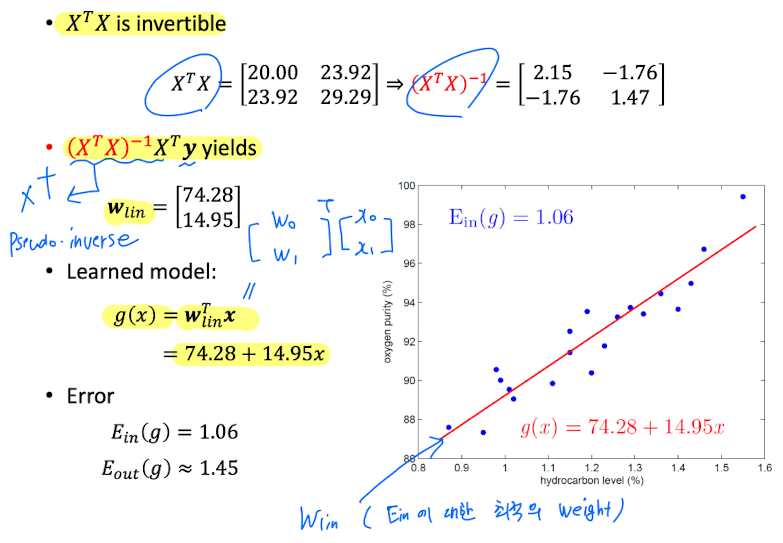
- 이 "한 번에" 계산되었기 때문에
1-step Learning이라고 한다. - 보통의 경우 Iterative하게 Learning이 진행되지만,
Regression은 1-Step으로 Learning이 완료되기 때문에
이것을closed-form solution이라고 하고, 매우 드문 Learning 방법이다.
- 이 "한 번에" 계산되었기 때문에