Week 2 | Neural Networks Basics | Python and Vectorization
Vectorization
-
In logistic regression, we need to compute
()
➡️ 여기서 는 차원의 vector이다.- If we had a
non-vectorized implementation, that's going to be really slow.z=0 # 차원 nx가 늘어날수록 연산이 더 늦어진다 for i in range(nx) : z += w[i] * x[i] z += b - If we had a
vectorized implementation, this is much faster.z=np.dot(w, x) + b
- If we had a
-
Python Example:
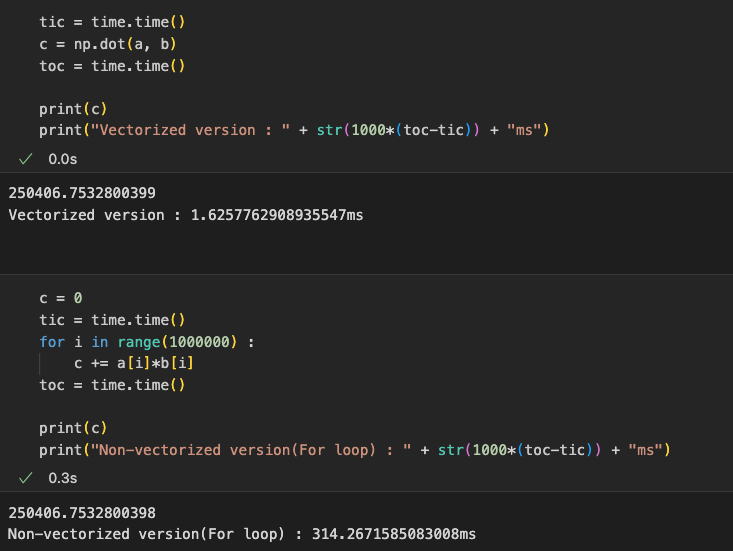
- Non-vectorized version took something like 300 times longer than the vectorized version
➡️ 따라서 code에 명시적 for loop 사용을 줄이고,
vectorization하면 훨씬 빠르게 연산할 수 있다. - GPU와 CPU는 parallelization instruction(SIMD : Single Instruction Multiple Data)처리가 가능하다.
SIMD는 for loop을 명시적으로 구현할 필요가 없는 다른 함수를 사용할 수 있다.
numpy는 병렬 처리를 더 잘 활용하여 계산을 훨씬 더 빠르게 수행할 수 있다.
- Non-vectorized version took something like 300 times longer than the vectorized version
More Vectorization Examples
Neural network programming guideline:
Whenever possible, avoid explicit for-loops :
Example 1
- (: matrix, :vector) 을 계산한다고 가정.
- Non-vectorized version : 2 for-loops 사용
u = np.zeros((n, 1)) for i ... for j ... u[i] += A[i][j] * v[j] - Vectorized version : 2 for-loops 사용하지 않아 훨씬 빠를 것임
u = np.dot(A, v)
- Non-vectorized version : 2 for-loops 사용
Example 2
- vector 가 이미 memory에 있고,
의 모든 요소에 exponential 연산을 적용하려 한다고 가정.
➡️- Non-vectorized version : 1 for-loop 사용
u = np.zeros((n, 1)) for i in range(n) : u[i] = math.exp(v[i]) - Vectorized version : 1 for-loop 사용하지 않아 훨씬 빠를 것임
import numpy as np u = np.exp(v)
- Non-vectorized version : 1 for-loop 사용
- np.exp() 외에도 다양한 NumPy bulit-in function이 존재
- np.log()
- np.abs()
- np.max()
- ...
Logistic regression derivatives
-
아래에 인 logistic regression에서
derivatives 계산을 위한 code가 있다.
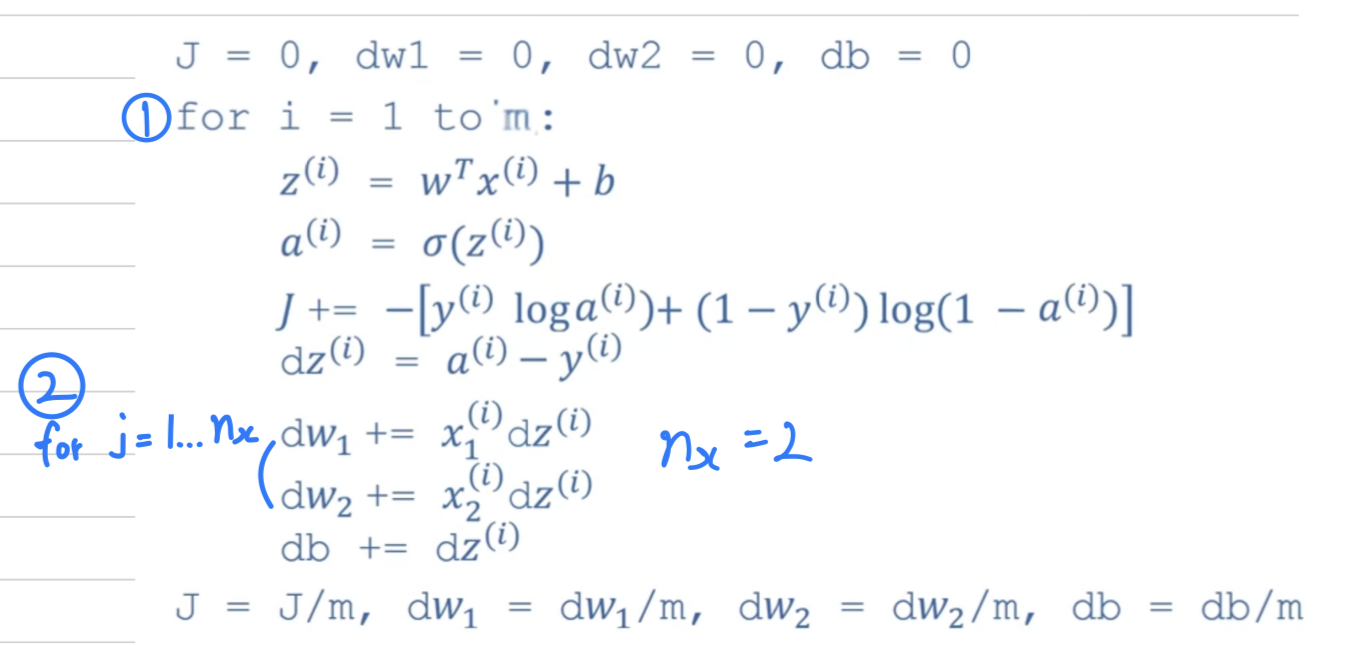 위 코드에서 차원이 늘어날수록 두번째 for문의 반복 횟수가 늘어날 것이다.
위 코드에서 차원이 늘어날수록 두번째 for문의 반복 횟수가 늘어날 것이다.
따라서 우리는 두번째 for문을 eliminate하고자 한다. -
두번째 for문을 제거하고,
one for-loop만 갖는 code로 변경하면 다음과 같다.
Vectorizing Logistic Regression
- Logistic regression 구현을 vectorization하여
전체 training set을 처리할 수 있는 방법을 살펴보자
Vectorization to compute prediction for m examples
Non-vectorization Implementation:
개의 training data가 있다면,
하나의 training data에 대하여 4개의 propagation step이 있고, 그것을 번 반복해야 한다.
 Vectorization으로 위 prediction 과정을 explicit for loop 없이 수행할 수 있다.
Vectorization으로 위 prediction 과정을 explicit for loop 없이 수행할 수 있다.Vectorization Implementation:- 개의 training data 들을 horizontally stacking하여
[] shape의 Matrix X를 만든다 - 개의 도 horizontally stacking하여
[] shape의 row vector 를 만든다 - Z = np.dot(, X) + b
연산을 수행하여
[] shape의 row vector 를 만든다. - A = sigmoid(Z)
연산을 수행하여
최종 prediction인 vector 를 얻는다.

- 개의 training data 들을 horizontally stacking하여
Vectorization to compute gradient for m examples
-
Non-vectorization Implementation:
개의 training data가 있다면,
하나의 training data에 대하여 개의 를 update 해야 하고,
그것을 번 반복해야 한다.
 Vectorization으로 위 gradient 연산 과정을 explicit for loop 없이 수행할 수 있다.
Vectorization으로 위 gradient 연산 과정을 explicit for loop 없이 수행할 수 있다. -
Vectorization Implementation:

Implementing Logistic Regression
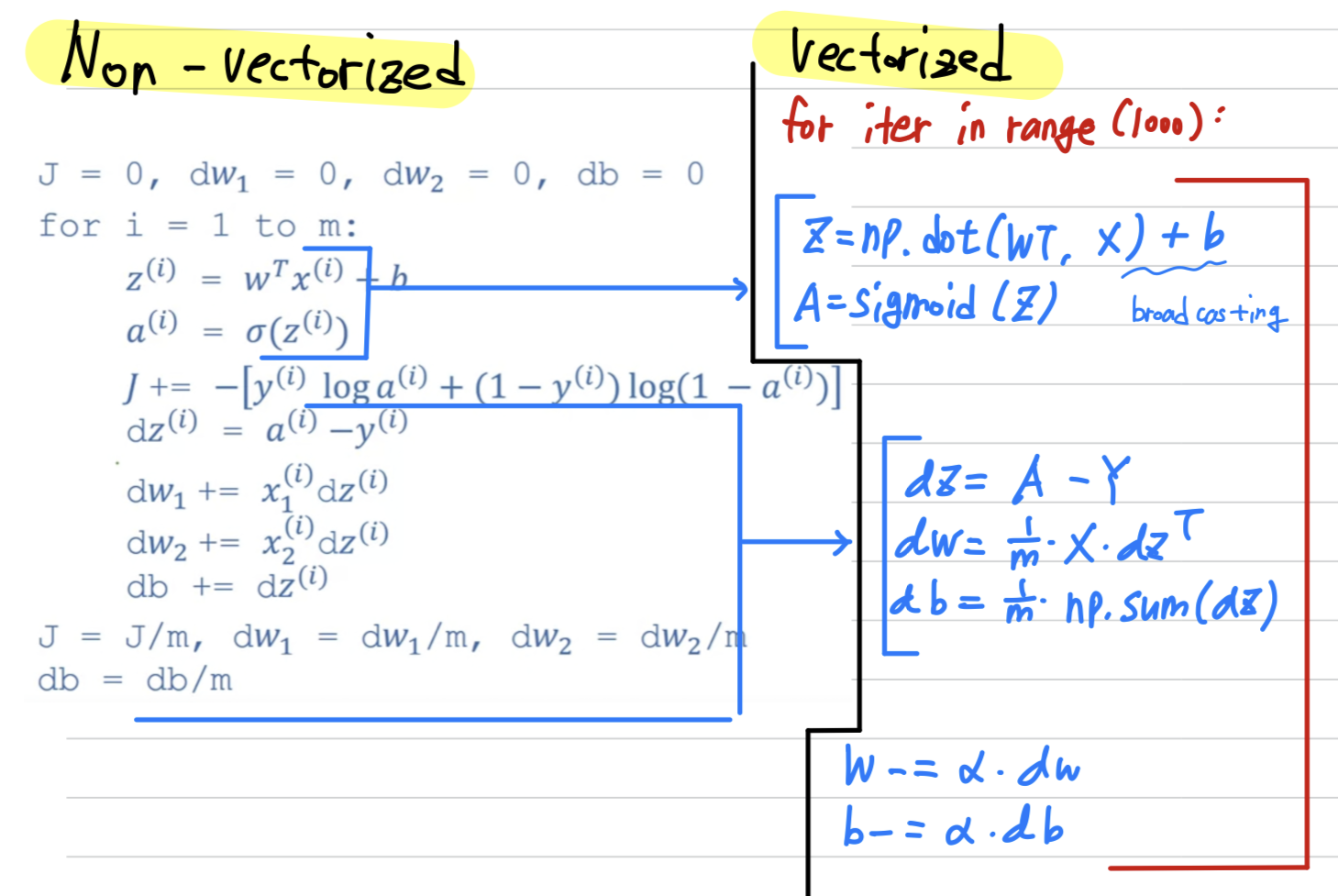
Broadcasting
Broadcasting example
- Carlories from Carbs, Proteins, Fats in 100g of different foods :
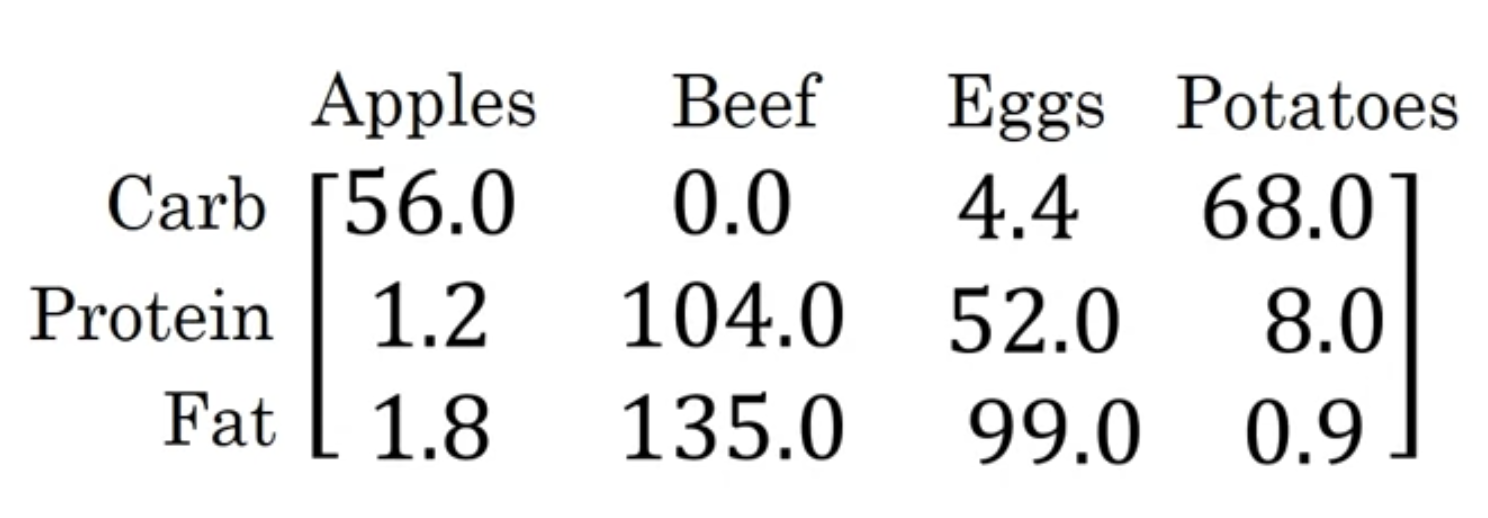
- Apple은 100g 중에서 56 calories의 Carb을 함유하고 있다.
Apple의 Carb이 calory를 차지하고 있는 비율은 다음과 같이 계산한다.
%
위 계산을 모든 식품의 모든 성분 별로 구하는 방법은 다음과 같다.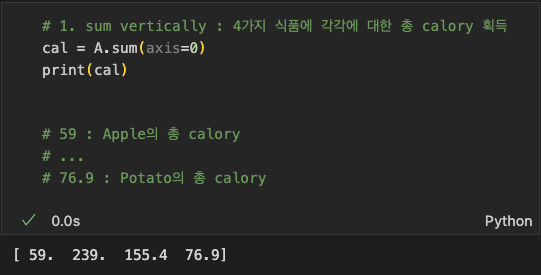
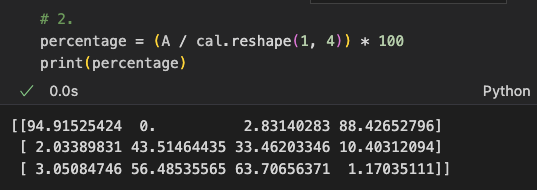
 위에서 어떻게 [3 x 4] matrix A를 [1 x 4] matrix cal로 나눌 수 있었을까?
위에서 어떻게 [3 x 4] matrix A를 [1 x 4] matrix cal로 나눌 수 있었을까?
➡️broadcasting
- Apple은 100g 중에서 56 calories의 Carb을 함유하고 있다.
Another example
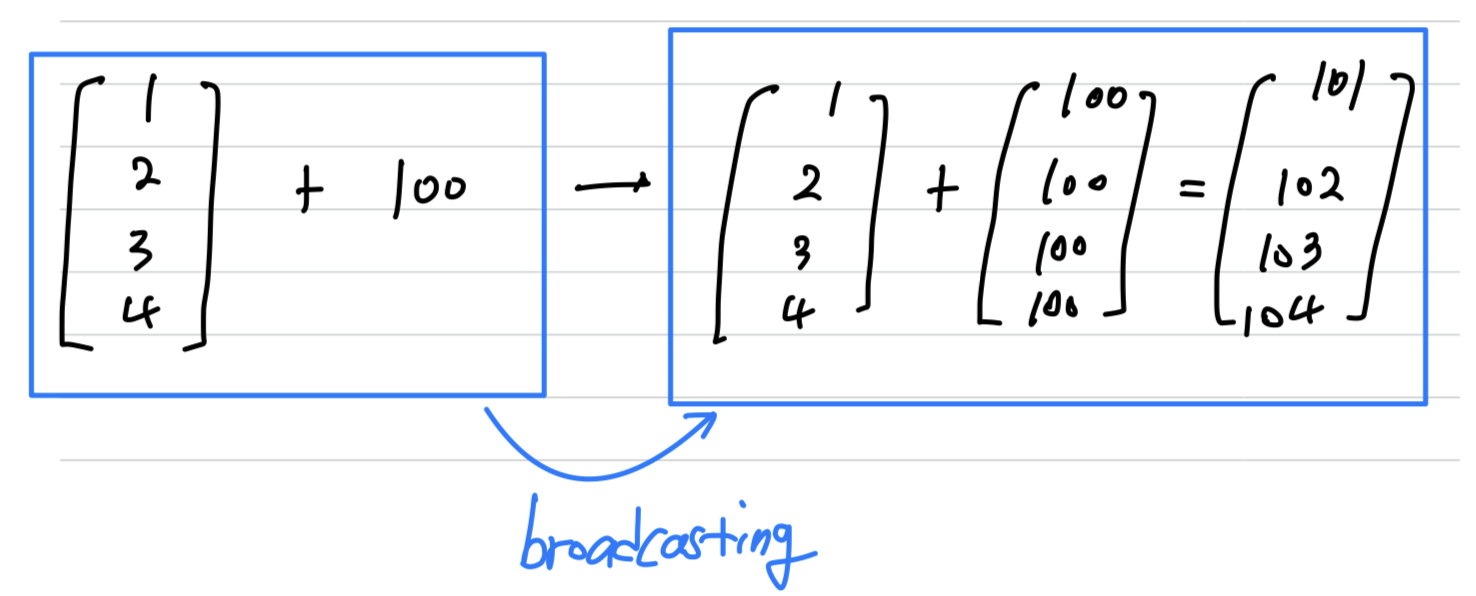

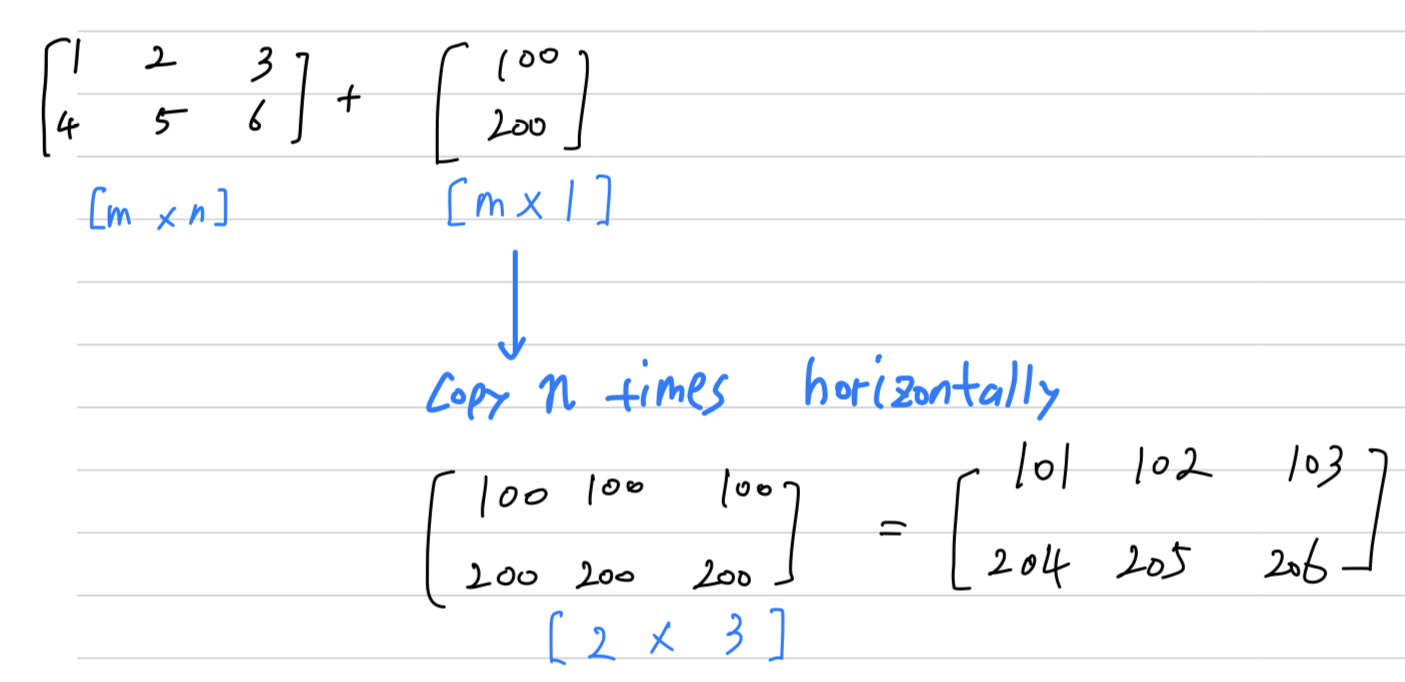
General Principle:- [m x n] matrix와 [1 x n] matrix끼리 연산할 때,
[1 x n]matrix는 수직 방향(vertically)으로 m번 copy되어 [m x n]matrix로 만들고나서
element-wise 연산을 수행한다. - [m x n] matrix와 [m x 1] matrix끼리 연산할 때,
[m x 1]matrix는 수평 방향(horizontally)으로 n번 copy되어 [m x n]matrix로 만들고나서
element-wise 연산을 수행한다.
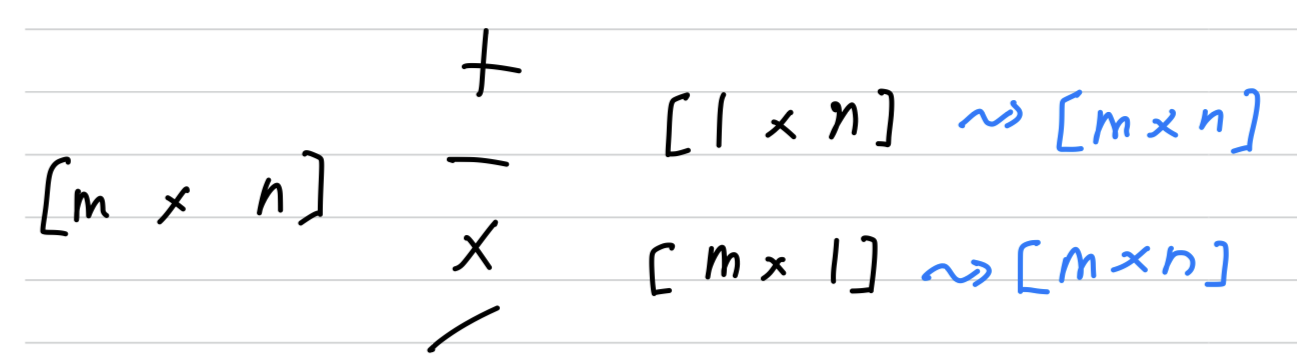
- [m x n] matrix와 [1 x n] matrix끼리 연산할 때,
A Note on Python/numpy
a = np.random.randn(5)rank 1 array ➡️ 이는 column vector나 row vector로 일관되게 동작하지 않기 때문에
Neural Network를 구성할 때, rank 1 array를 사용하지 않는 것이 좋다.
a.shape = [5, ]
a = np.random.randn(5, 1)이는 column vector로 일관되게 동작한다
a.shape = [5 x 1]
a = np.random.randn(1, 5)이는 row vector로 일관되게 동작한다
a.shape = [1 x 5]
따라서 1 rank array를 사용하지 않는 것이 좋다.
column vector인지 row vector인지 일관되게 동작할 수 있도록 vector를 생성해야 한다.
만약 1 rank array가 code상에 존재한다면, a = a.reshape()을 통해
column vector인지 row vector인지 확실히 명시해야 한다.
Explanation of logistic regression cost function
- where
we want to interpret as the
so we want to our algorithm to output as the chance
that for a given set of input features
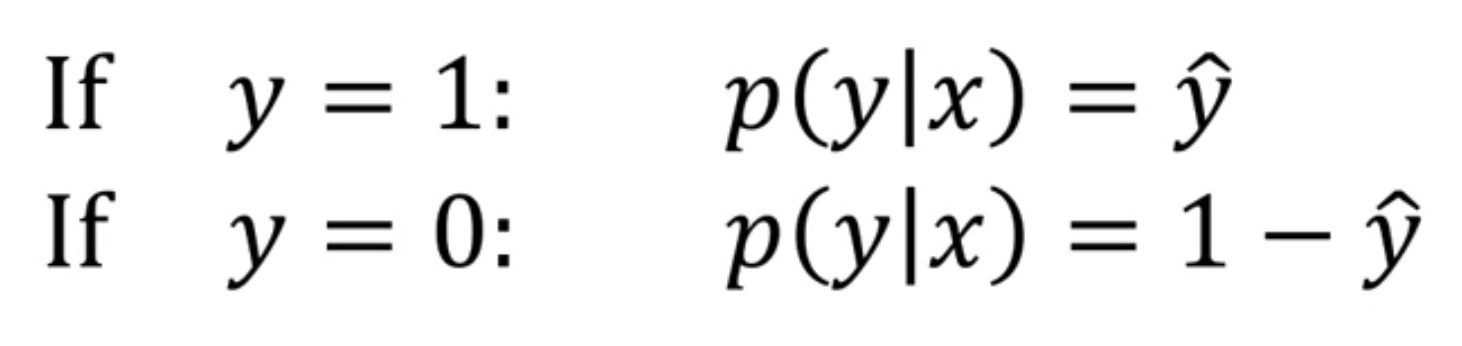
위 두 개의 식을 요약하면 다음과 같다.
➡️
또한 함수는 monotonically increasing function(단조 증가 함수)이기 때문에
를 maximization하는 것이
를 optimization하는 것과 유사하다.
➡️
또한일반적으로Loss function는 minimization하는 것이 목적이므로
에 (-)부호를 붙인다.
그래서 결과적으로 을 maximization하는 것은
를 minimization하는 것과 같아진다.
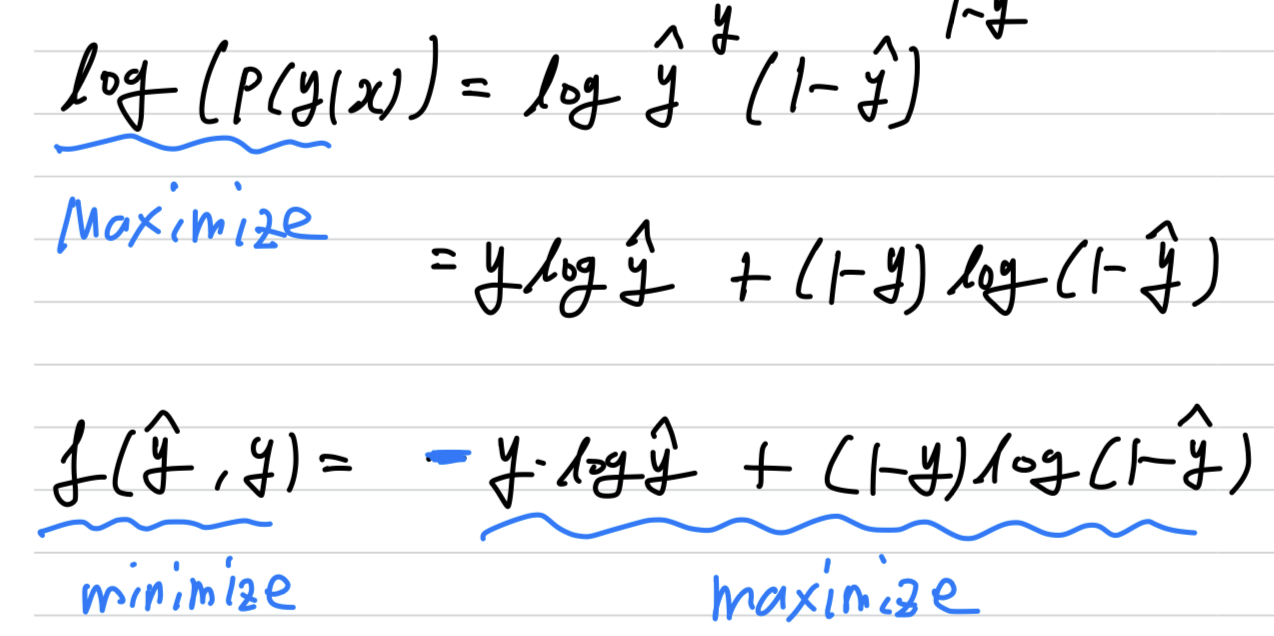
- 그렇다면
Cost Function은 어떨까?
training set의 모든 label의 probability는 다음과 같다.
