관계형 DB에서의 Query

• 관계형 DB를 사용하는 단계

  1. Design schema
  2. Load data
  3. execute quries

• 관계형 DB의 query는 high-level language로 표현됨.

• 관계형 DB의 query 결과는 Relation(Table)이다.

• Query 언어

  1. 관계 대수 (Relational Algebra) :
     실제 사용하는 언어 x, 수학적 기호
  2. SQL (Structured Query Language) :
     실제 computer에서 사용하는 언어

관계 대수 연산의 종류

• 수학적 집합 연산 : 합집합, 교집합, 차집합, cartesian product
  (Table들의 집합, Table은 tuple들의 집합으로 되어있기 때문에 집합 연산 필요)
• 관계 DB를 위한 특별 연산 : select, project, join

관계대수

select

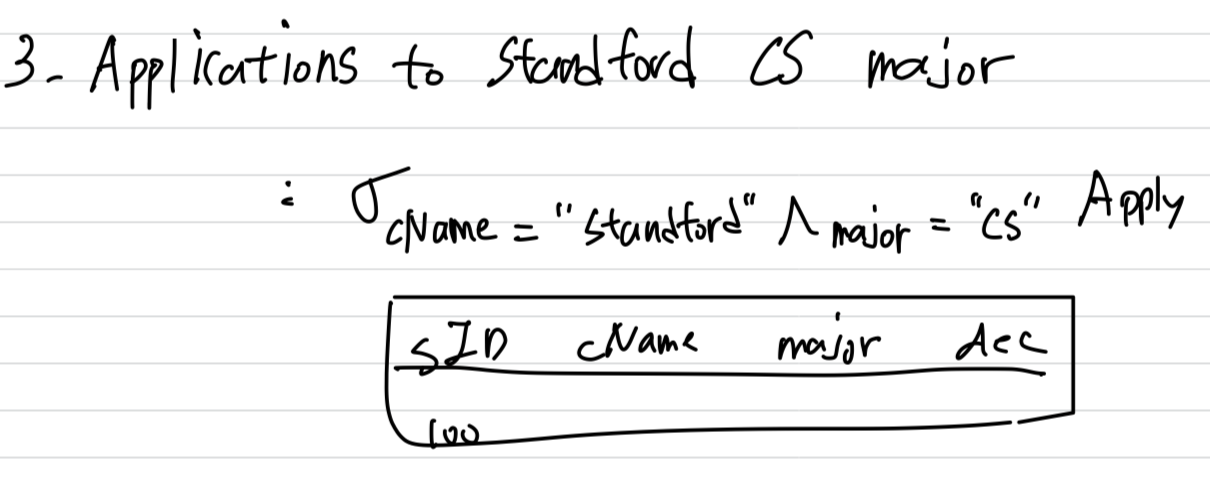
• select : Relation R에서 조건을 만족하는 tuple을 선택

  $\sigma_{<선택조건>}(R)$

• example :
  

project

• project : Relation R에서 attribute list에 명시된 attribute들만 선택

  $\Pi_{<attributelist>}(R)$

• example :
  

Cartesian Product

• Cartesian Product : table의 tuple들간의 모든 조합을 만듦

  $A=\{1, 2\}$, $B=\{a, b, c\}$
  $A$ X $B$ = $\{(1,a), (1,b), (1,c), (2,a), (2,b), (2,c)\}$

• 카티션 곱 자체로는 의미가 없음. 잘못된 정보들이 포함되어 있기 때문.
  

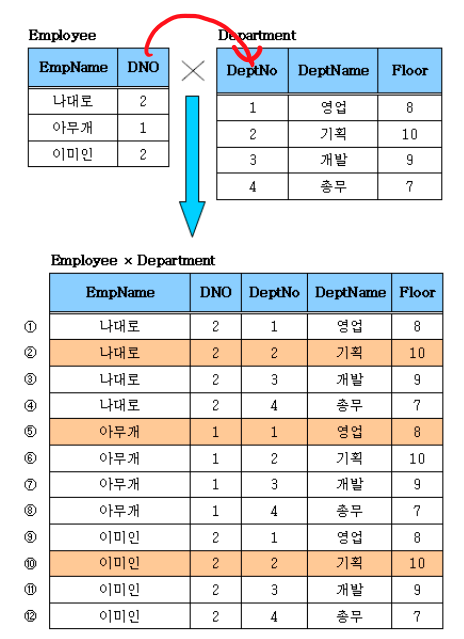
• exampmle :
  

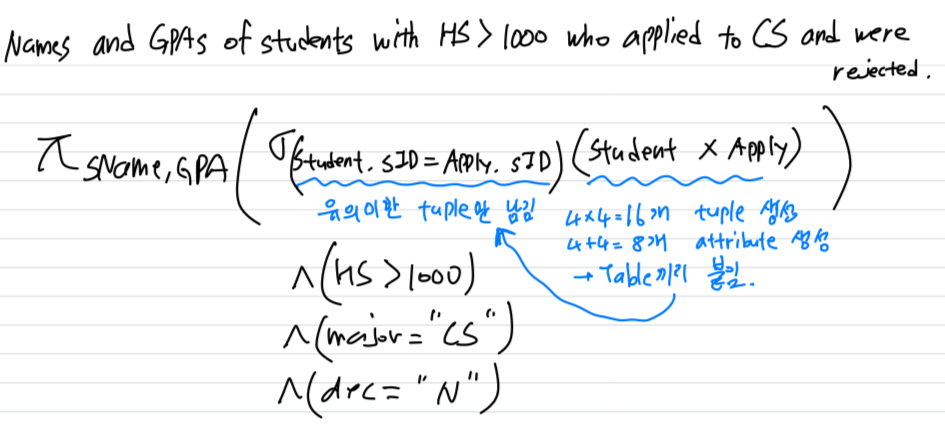
Natural Join

• Natural Join :
  T1 table과 T2 table에 같은 이름의 attribute에서 같은 값을 갖는 tuple만 생성
  꼭 필요한 연산은 아님. (카티션 곱을 편리하게 사용하기 위한 연산)

  $T1 \bowtie T2 = \sigma_{T1[a]=T2[a]}(T1$ X $T2$)

• example :
  
  

Theta Join

• Theta Join :
  T1 table과 T2 table에서 조건($\theta$)에 해당하는 tuple만 join.

  $T1 \bowtie_\theta T2 =\sigma_\theta(T1)$ X $(T2)$

• example :
  

join selectivity(선택률)

• join selectivity : 결과 tuple 수 / 조합 가능한 전체 tuple 수
  

합집합

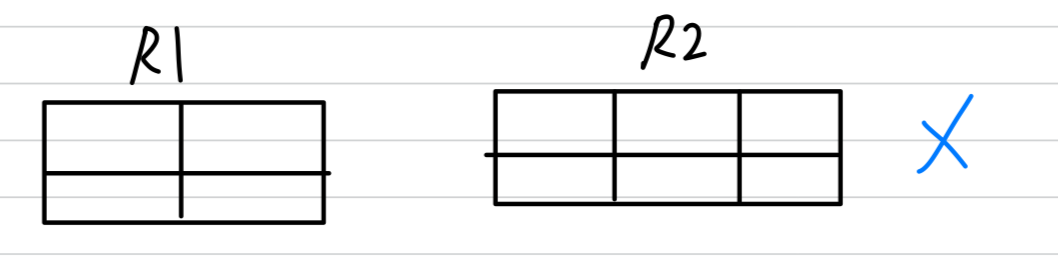
• R1 U R2 : 무조건 할 수 없다.
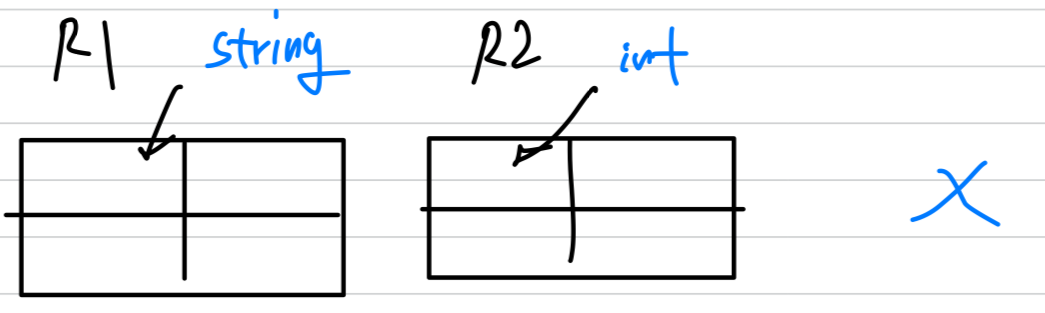
• 조건 1 : attribute 개수가 같아야 함
  
  조건 2 : 대응되는 attribute들의 domain이 호환성을 가져야 함
  
• example :
  

차집합

• $\Pi_{key}(T1)$ - $\Pi_{key}(T2)$
  

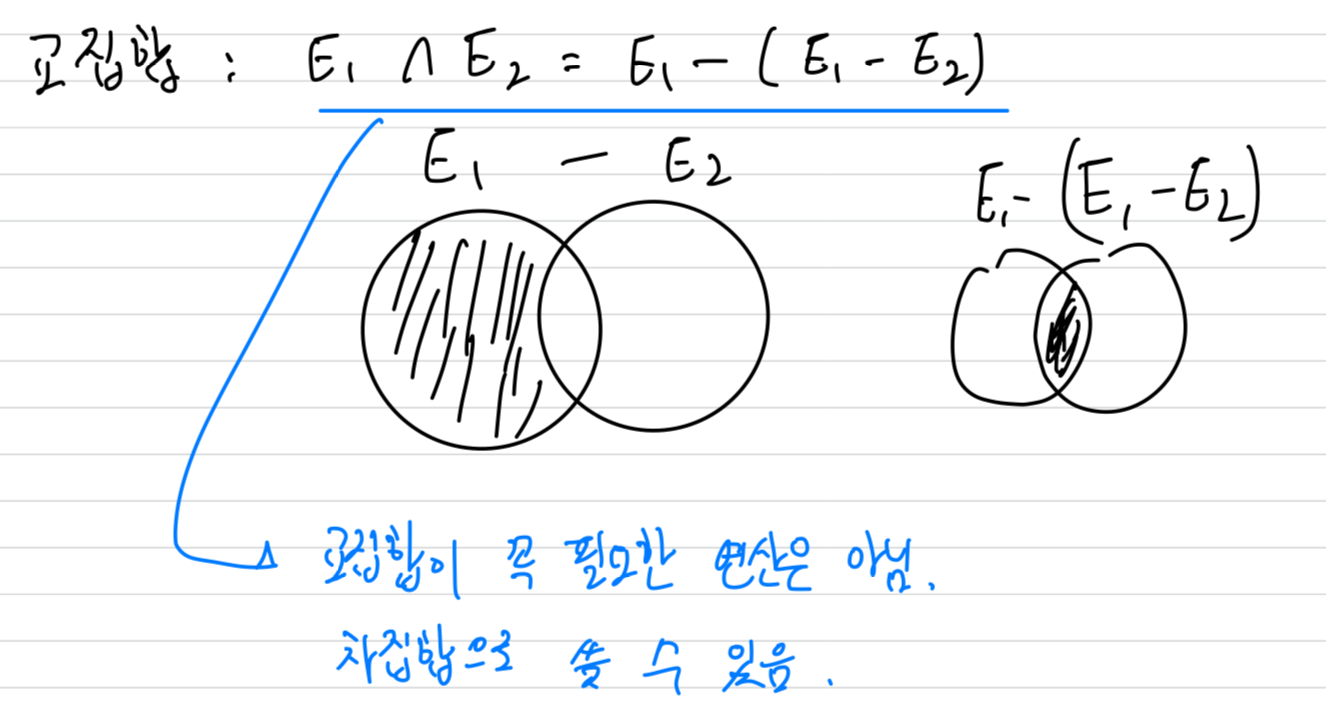
교집합

• 교집합 연산은 연산의 능력을 증가시키지는 않음
  
  
• example :
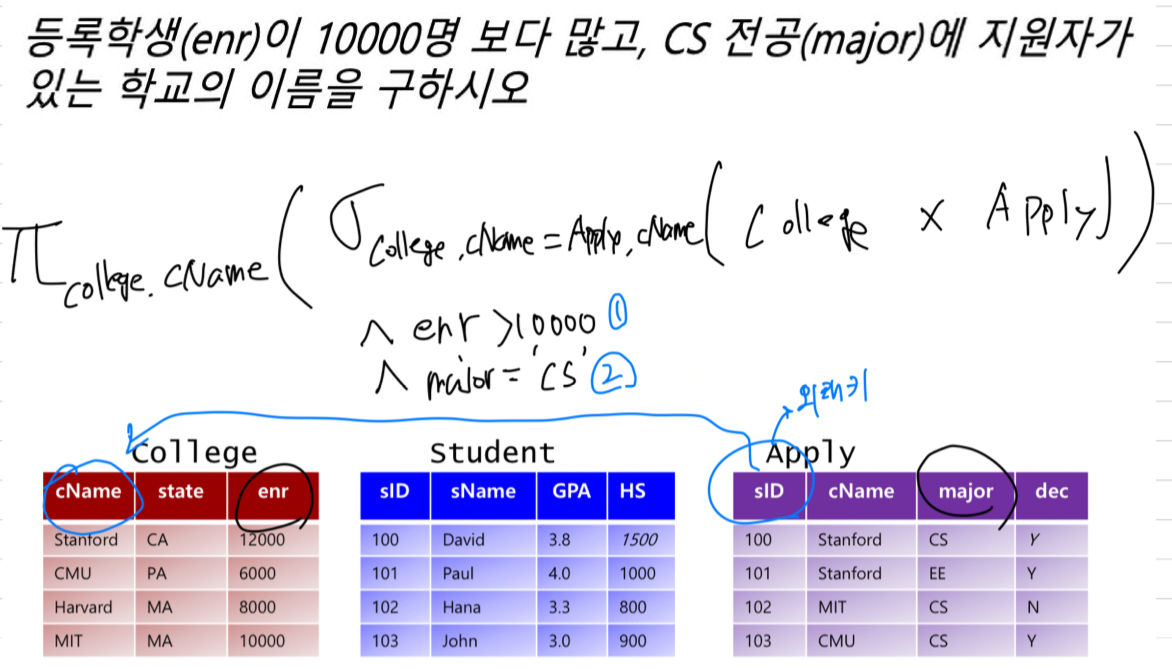
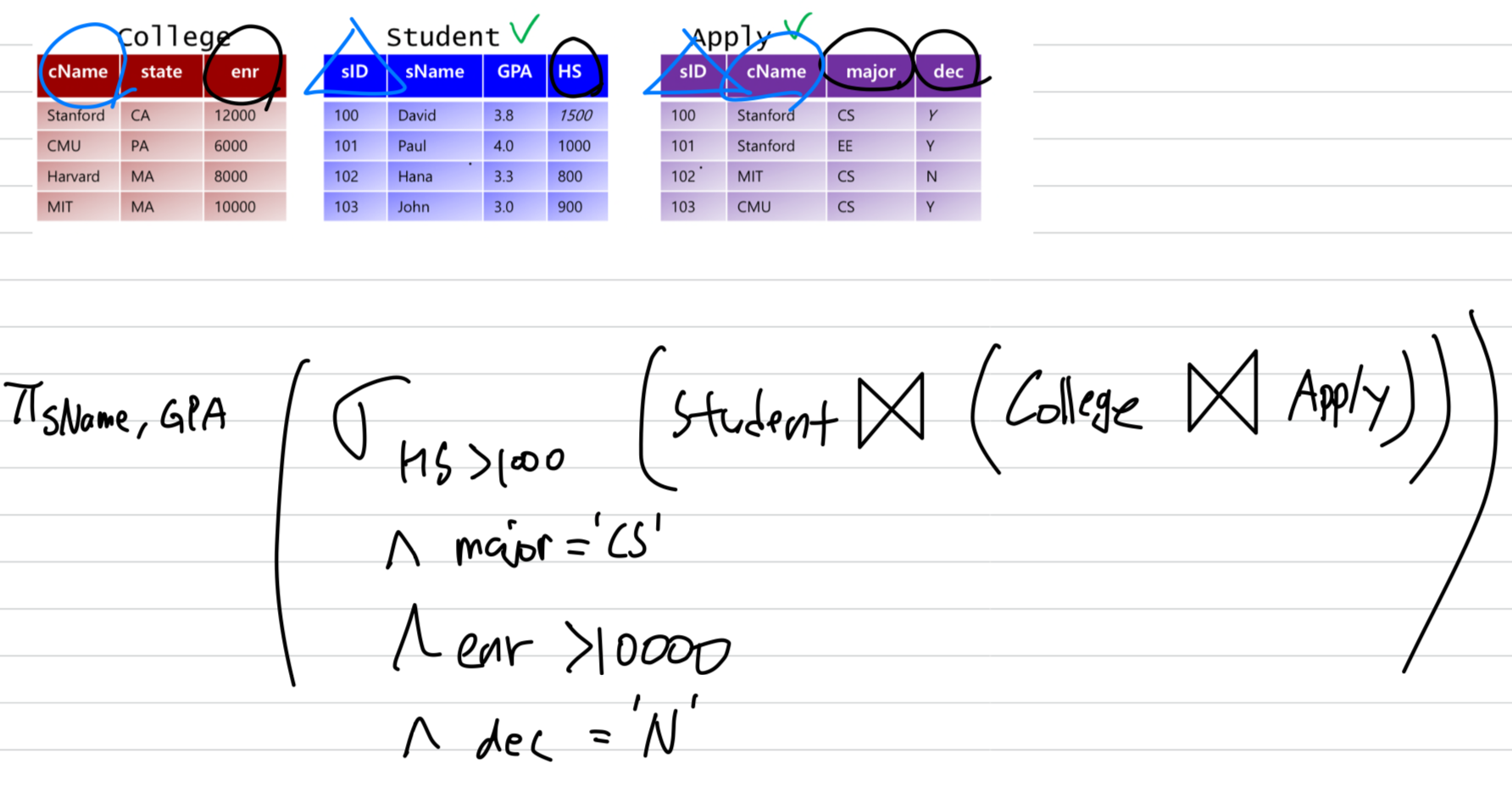
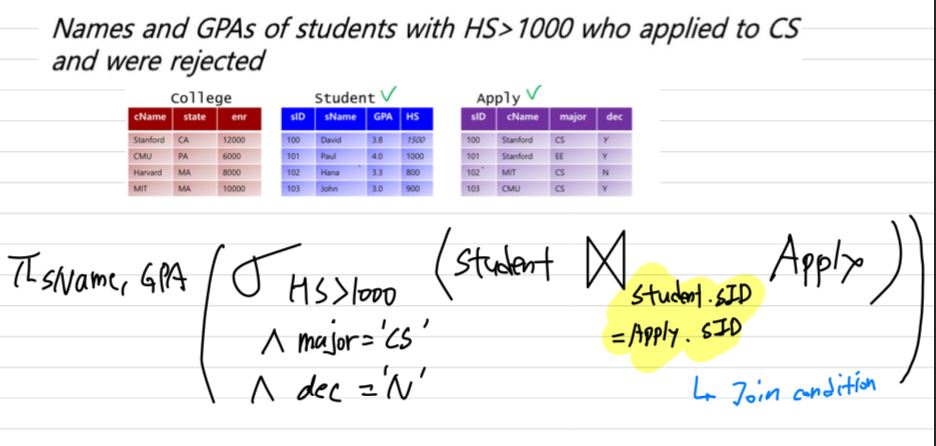
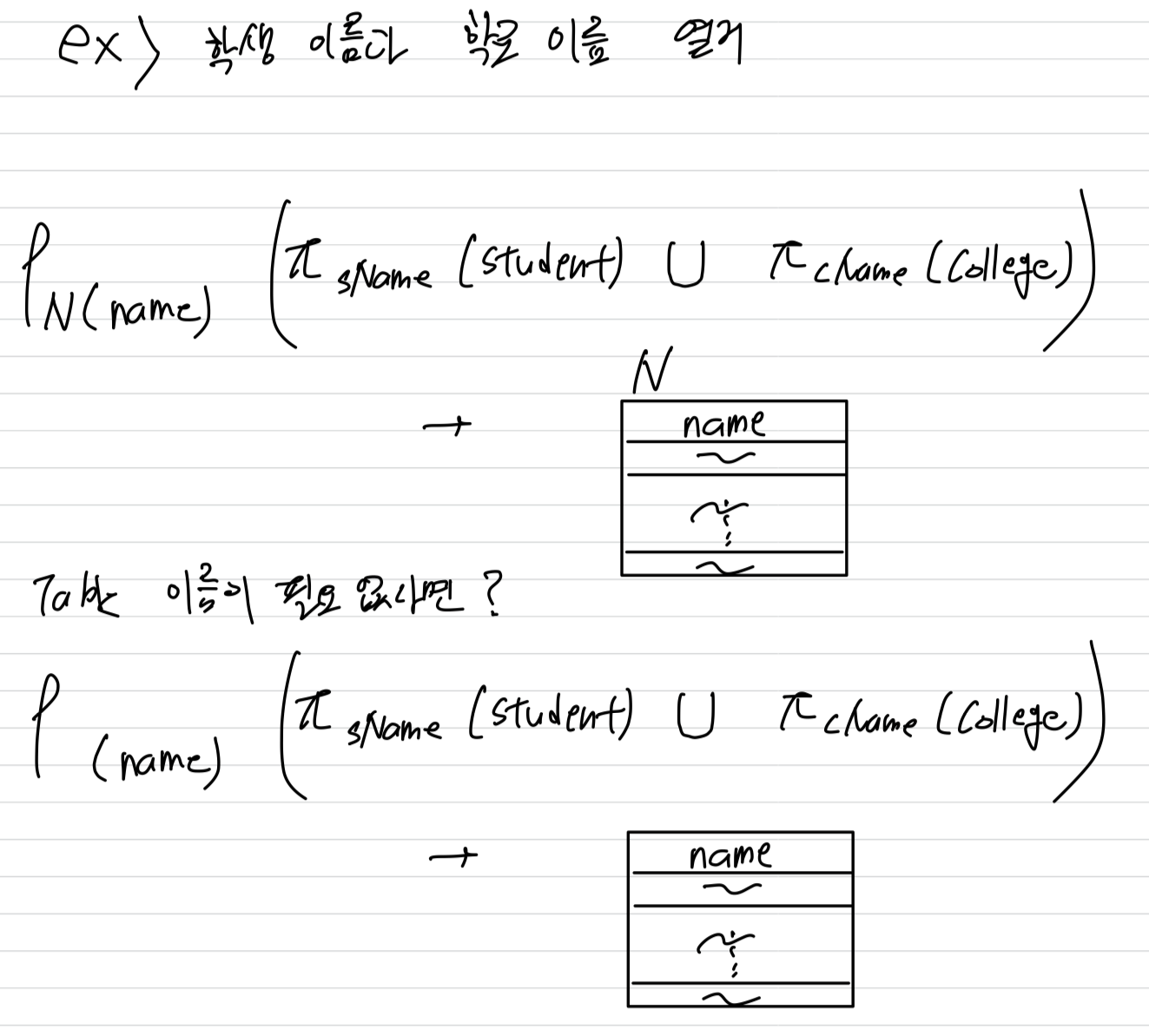
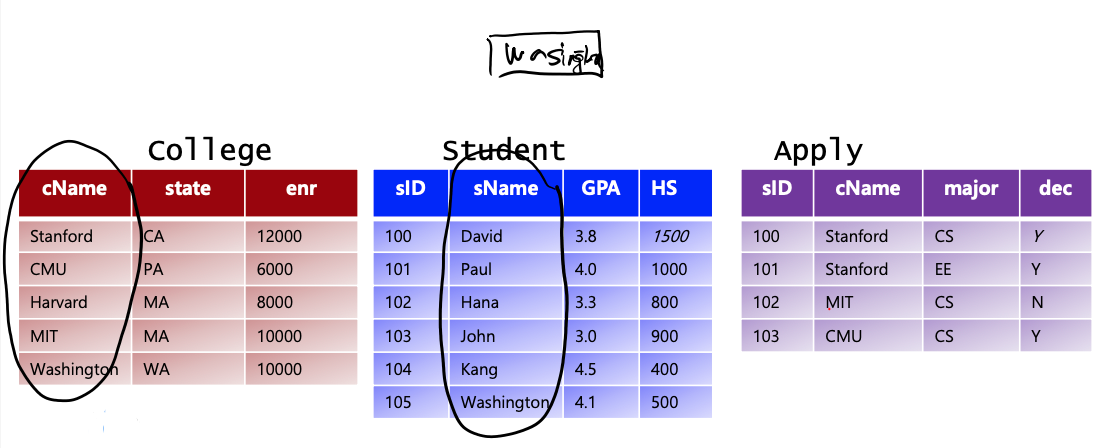
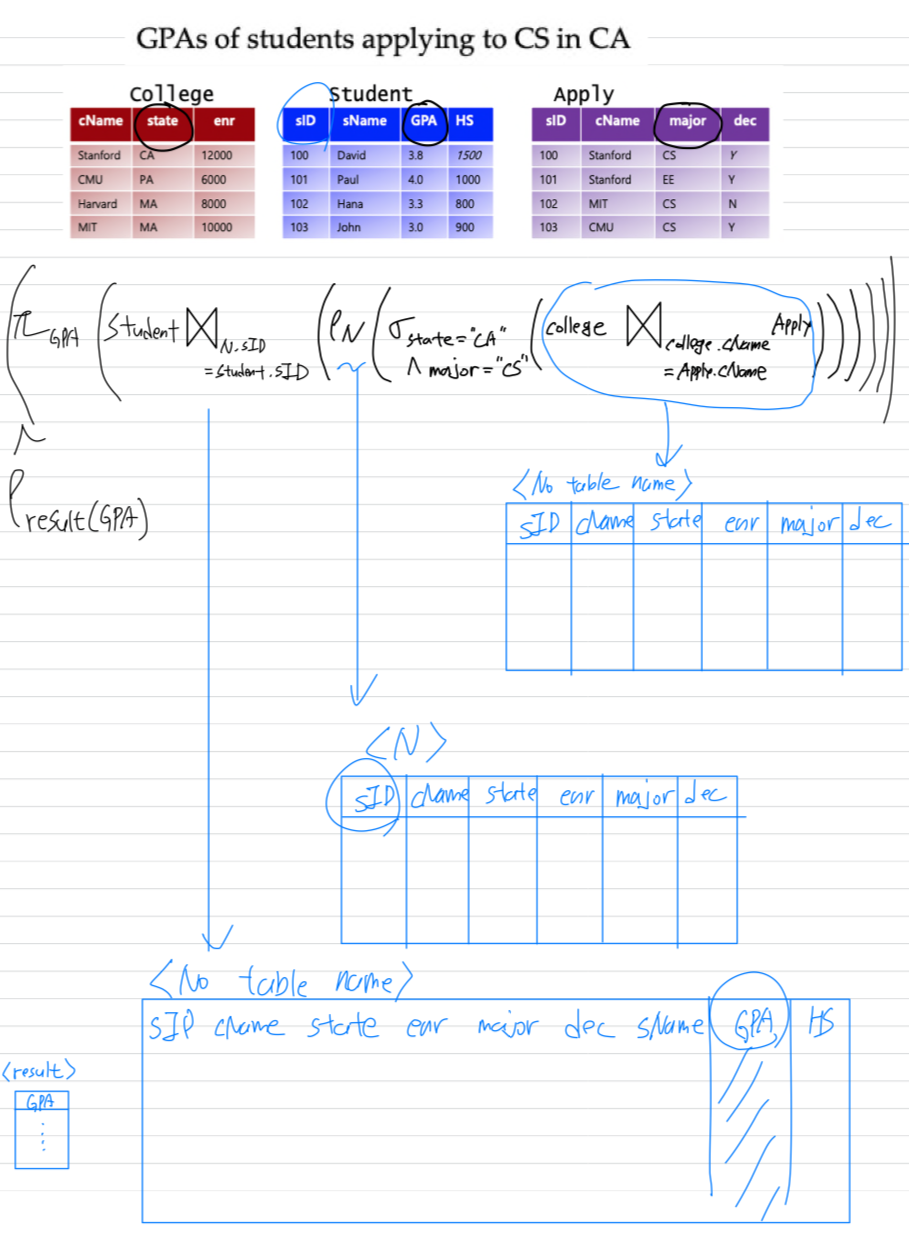
  학생이름과 학교이름으로 동시에 사용되는 이름을 구하라.
  
  

재명명(renaming) 연산자

• renameing 연산자 : Relation 이름과 attribute 이름을 모두 변경

  $\rho_{S(B1, B2, ..., Bn)}(E)$
  $S$ : 새로운 Relation 이름
  $B_1, .., B_n$ : 새로운 attribute 이름

• self join시 이름 간의 모호함을 제거하기 위해 필요
  

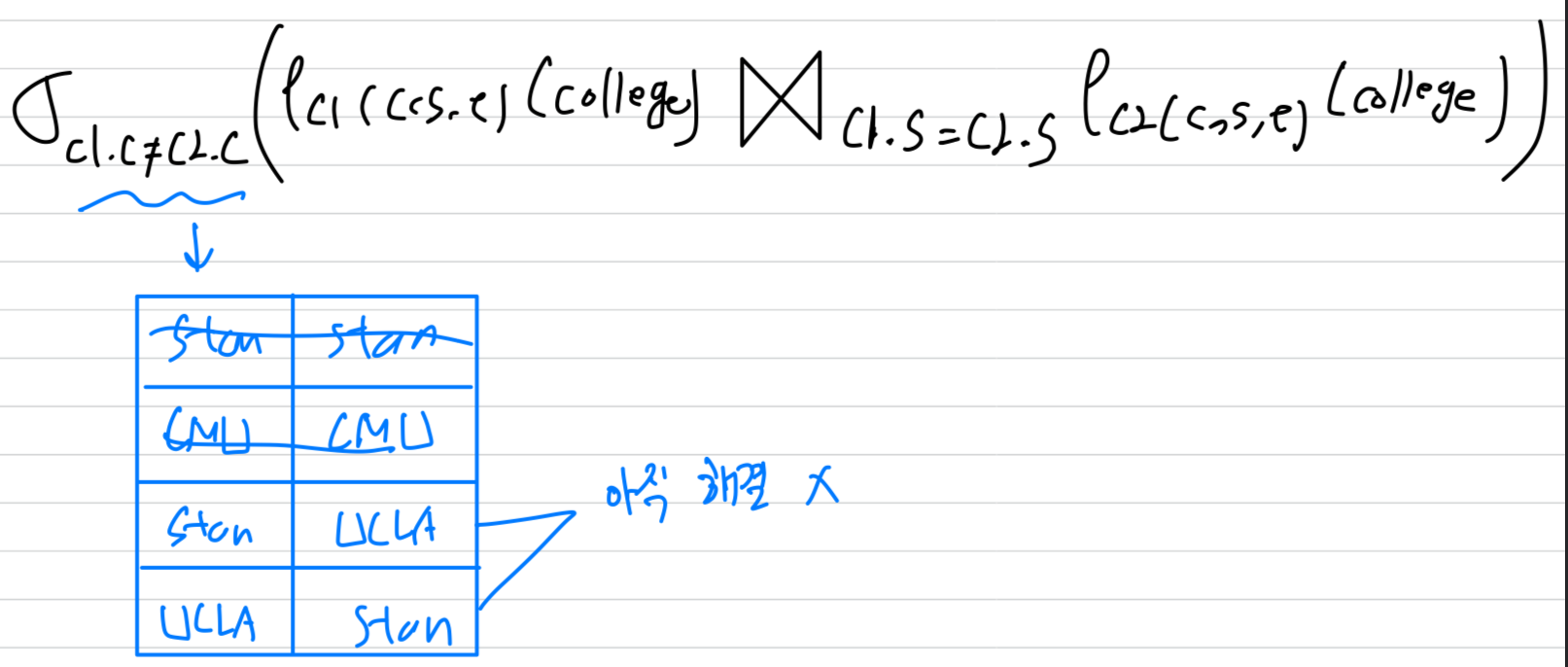
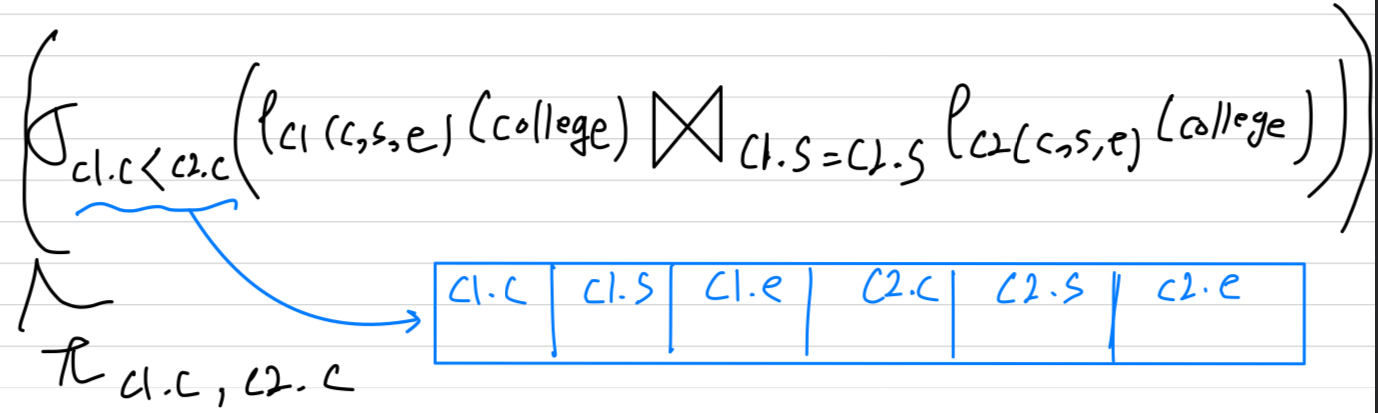
Summary

• 핵심으로 필요한 연산과 그렇지 않은 연산자 분류
  
  

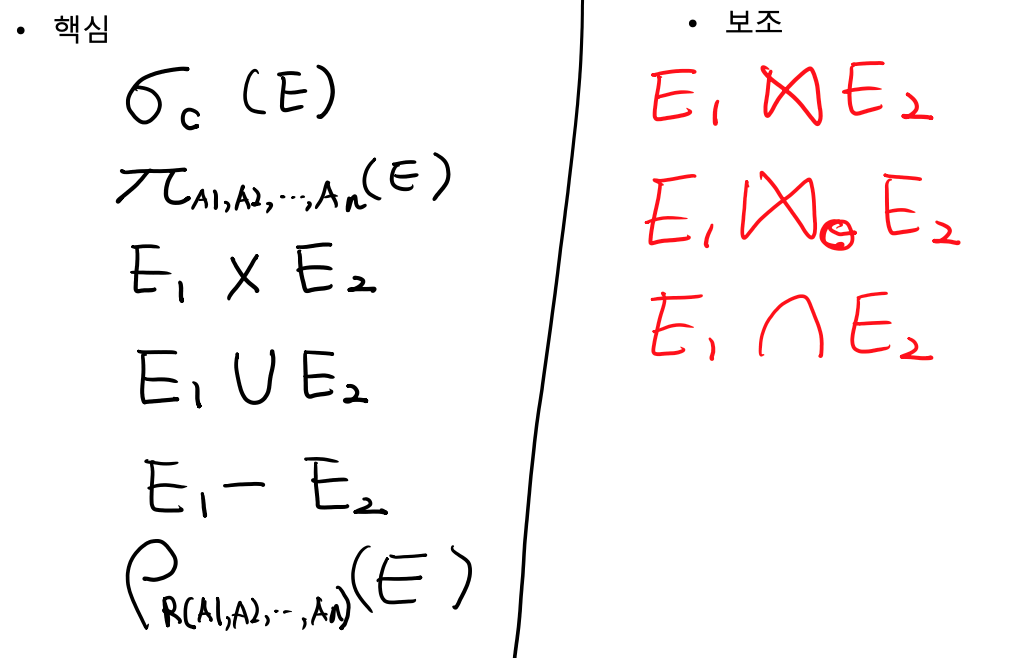
assign을 통한 다른 표현법

• 같은 주에 있는 학교의 쌍을 열거하라
  
  

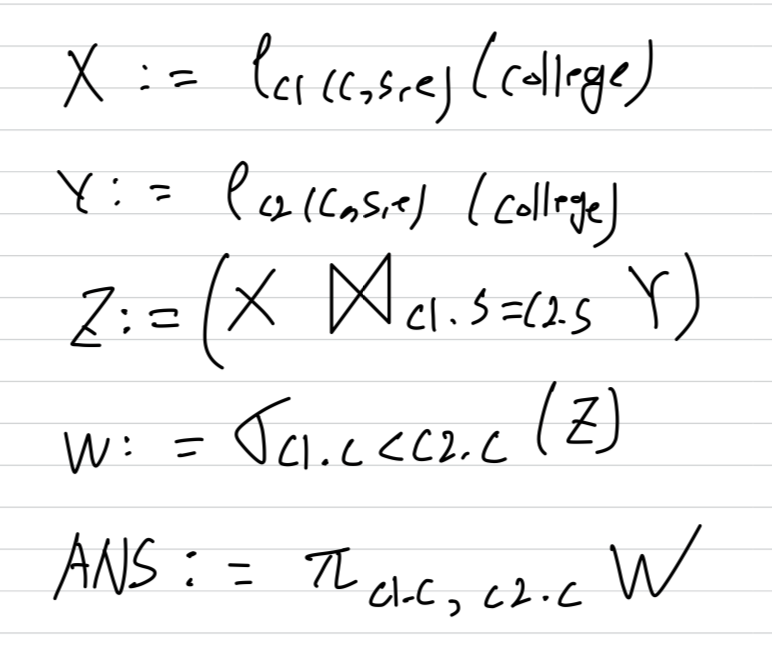
query tree를 통한 다른 표현법

위의 query를 tree로 나타내면,