Generative Adversarial Nets (GAN)

홍선재·2025년 5월 25일

국민대학교 인공지능학회 (XAI)

목록 보기

11/11

Abstract

경쟁하는 과정을 통해 generative model을 추정하는 새로운 프레임워크 제안
2개의 모델 학습

generative model(생성 모델), G : training data의 분포를 모사함 → discriminative model이 구별하지 못하도록 한다.
discriminative model(판별 모델), D : samle 데이터가 G로부터 나온 데이터가 아닌 실제 training data로부터 나온 데이터일 확률을 추정한다.
- G를 학습하는 과정은 D가 sample 데이터가 G로부터 나온 가짜 데이터와 실제 training data로부터 나온 데이터일 확률을 추정
- 이 논문에서는 이와 같은 프레임워크를 minimax two-player game으로 표현하고 있다. 이는 논문에서 나오는 방정식으로 확인이 가능
- 임의의 함수 G,D의 공간에서 G가 training 데이터 분포를 모사하게 되면서 D가 실제 training 데이터인지 G가 생성해낸 가짜 데이터인지 판별하는 확률은 1/2이 된다.(즉, 실제 데이터와 G가 생성해내는 데이터의 판별이 어려워짐 )
- G와 D가 multi-layer perceptrons으로 정의된 경우 전체 시스템은 back-propagation을 통해 학습된다.

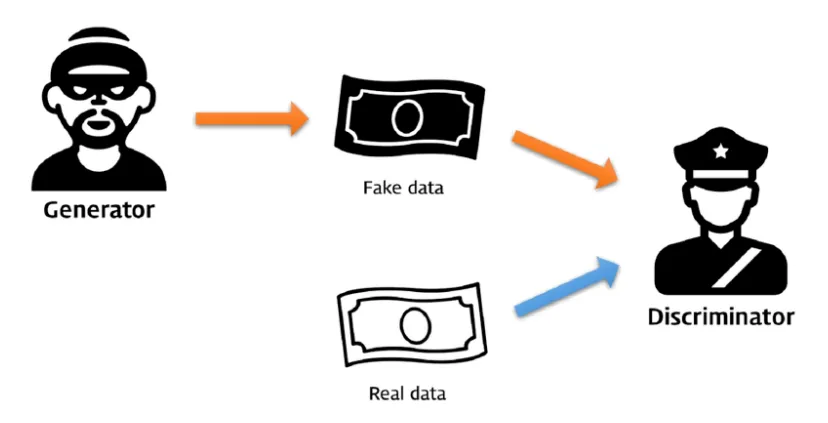
이 논문에서는 GAN이라는 새로운 프레임워크를 제안하고 있으며 생성 모델(G)과 판별 모델(D) 두가 지 모델을 학습하여 G는 실제 training data의 분포를 모사하며 그와 비슷한 데이터를 생성하려고 D는 실제 데이터와 G가 생성해낸 데이터를 구별하려하는 경쟁적인 과정으로 이루어져 있다.

1. Introduction

딥러닝의 눈에 띄는 성공들은 주로 판별 모델(discriminative models), 즉 고차원의 복잡한 센서 데이터를 클래스 레이블로 매핑하는 모델에 의해 이루어졌다. 예를 들어서 이미지 분류나 감정 분석 같은 작업들이 이에 해당한다.

이러한 성공은 대부분 backpropagation과 dropout 알고리즘 그리고 부분 선형 함수(piecewise linear unit)를 사용하는 신경망 덕분이다. 이들은 계산이 안정적이고 그래디언트도 잘 정의되어 있어서 학습이 잘된다.

반면 생성 모델(generative models)은 상대적으로 성과가 적었다.

maximum likelihood estimation이나 그와 관련된 방법들이 수학적으로 매우 복잡하거나 근사 계산이 어렵기 때문입니다.
판별 모델에서 잘 작동하는 부분 선형 함수가 생성 모델에서는 그다지 효과적이지 않기 때문입니다.

이러한 문제를 해결하기 위해 저자들은 새로운 생성 모델 학습 방법을 제안한다. 그것이 바로 Adversarial Nets(적대적 신경망)이다.

이 프레임워크에서는 생성 모델이 하나의 adversary(적대자)와 경쟁한다. 이 적대자는 진짜 데이터와 생성된 데이터를 구분하려는 discriminative model(판별 모델)이다. 이 구조는 마치 위조 지폐범(생성 모델)과 경찰(판별 모델) 간의 게임과 유사하다. 위조범은 진짜 같은 지폐를 만들어내려고 하고, 경찰은 그것을 잡아내려고 한다. 서로 경쟁하면서 두 모델은 계속 발전하게 된다.

이런 게임 기반 프레임워크는 다양한 모델과 최적화 알고리즘에 적용할 수 있다. 이 논문에서는 특히 생성 모델과 판별 모델 모두를 다층 퍼셉트론으로 설정한 특수한 경우를 다룬다. 이를 Adversarial Nets이라고 부른다.

이 경우에는 역전파(backpropagation)와 dropout만으로도 두 모델을 모두 학습시킬 수 있으며 생성 모델에서 샘플을 얻는 것도 forward propagation만으로 학습 가능하다. 복잡한 추론 과정이나 Markov chains도 필요없다.

"기존의 latent variables(잠재 변수)를 가진 생성 모델로는 크게 두 가지 계열이 있다. 하나는 확률 분포를 명시적으로 정의하고 학습하는 방식(Undirected 및 Hybrid Models)이며, 다른 하나는 분포보다는 샘플 생성 과정 자체를 중심으로 학습하는 방식이다. 각각의 방식은 확률 밀도 정의, 정규화 상수 계산, 학습 속도 및 안정성 등의 측면에서 서로 다른 장단점을 가진다."

1. Undirected Graphical Models (비지도 그래프 모델)

Restricted Boltzmann Machines (RBMS)
Deep Boltzmann Machines (DBMs)

이들은 변수들 간의 상호작용을 정규화되지 않은 잠재 함수들의 곱(product of unnormalized potential functions)으로 나타내고 전체 확률을 얻기 위해서는 모든 상태에 대해 전역적인 합/적분(=partition function)을 계산해야 한다. 하지만 이 partition function은 대부분의 경우 계산이 불가능하며 그로 인한 그래디언트 추정도 어렵다. 이를 보완하기 위해 보통 MCMC(Markov Chain Monte Carlo)방법이 사용되지만 믹싱 문제로 인해 학습이 매우 느리고 안정적이지 않다.

2. 혼합 모델(Hybrid Models)

Deep Belief Networks (DBNs)

DBNs는 한 개의 RBM(undirected layer)과 여러 개의 directed layer를 결합한 구조이다. 층별로 빠른 근사 학습이 가능하지만 directed 모델의 복잡성 + undirected 모델의 복잡성을 동시에 가지므로 계산 비용이 크다.

3. 대안적인 학습 기준

기존의 log-likelihood를 근사하거나 바운드하지 않는 방식들도 제안되어왔다.

Score Matching
Noise Contrastive Estimation (NCE)

이들은 모두 확률 밀도 (probability density)를 (정규화 상수는 모른채) 수학적으로 명시할 수 있어야 한다. 하지만 DBN, DBM 같은 복잡한 다층 생성 모델에서는 정규화되지 않는 밀도조차 유도하기 어려운 경우가 많다.

또한, NCE는 고정된 노이즈 분포를 사용하여 생성 모델을 학습한다. 이는 초기에는 효과적이지만 모델이 어느 정도 정답 분포를 학습한 이후에는 학습 속도가 급격히 느려지는 문제가 있다.

4. 샘플 생성에 초점을 맞춘 접근

어떤 방식들은 확률 분포를 직접 명시하지 않고 단순히 샘플을 잘 생성하는 machine을 학습시킨다. 이 방식은 보통 backpropagation으로 학습이 가능하단 장점이 있다.

GSN (Generative Stochastic Networks)은 일반화된 Denoising Auto-Encoder의 확장으로, 이들 모두는 하나의 생성 마르코프 체인의 한 단계를 수행하는 기계를 학습한다고 볼 수 있습니다.

그러나 GSN은 마르코프 체인을 통한 반복적인 샘플링 과정이 필요합니다.

GAN(Adversarial Nets)의 차별점

GAN은 마르코프 체인 없이도 샘플을 생성할 수 있는 구조이다. 또한 feedback loop 없이 샘플을 생성할 수 있기 때문에, 역전파 과정에서 유리한 부분 선형 유닛(piecewise linear units)을 효과적으로 활용할 수 있다. 기존의 생성 모델에서는 이러한 유닛들이 feedback 구조로 인해 활성값 폭주(unbounded activation) 문제를 일으킬 수 있었지만, GAN에서는 이러한 문제가 발생하지 않는다.

GAN과 유사하게 명시적인 확률 분포를 정의하지 않고 샘플링을 중심으로 학습하는 방식으로는 다음과 같은 모델들이 있다:

Auto-Encoding Variational Bayes (VAE)
Stochastic Backpropagation

이들은 GAN보다 먼저 또는 비슷한 시기에 제안되었으며, 모두 backpropagation을 기반으로 한 학습이 가능하다는 공통점이 있다.

3. Adversarial nets

adversarial modeling 프레임워크는 앞서 말했듯이 가장 간단하므로 mult-layer perceptrons 모델 적용한다.

학습 초반에는 G가 생성해내는 이미지는 D가 G가 생성해낸 가짜 샘플인지 실제 데이터의 샘플인지 바로 구별할 수 있을 만큼 형평없어, D(G(z))의 결과가 0에 가깝다. 즉 , z로부터 G가 생성해낸 이미지가 D가 판별하였을 때 바로 가짜라고 판별할 수 있다고 하는 것을 수식으로 표현한 것이다. 그리고 학습이 진행될수록 G는 실제 데이터의 분포를 모사하면서 D(G(z))의 값이 1이 되도록 발전한다. 이는 G가 생성해낸 이미지가 D가 생성해낸 이미지가 D가 판별하였을 때 진짜라고 판별해버리는 것을 표현한 것이다.

$\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]$

$D(x)$ : 진짜 데이터일 확률을 출력하는 판별자(Discriminator)의 출력
$G(z)$ : 잠재 변수 zzz로부터 가짜 데이터를 생성하는 생성자(Generator)의 출력
$p_{data}(x)$ : 실제 데이터 분포
$p_z(z)$ : 잠재 공간(latent space)의 분포, 보통 정규분포 $\mathcal{N}(0,1)$

$\mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)]$ : real data x를 discriminator에 넣었을 때 나오는 결과를 log 취했을 때 얻는 기댓 값

$\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z))]$ : fake data z를 generator에 넣었을 때 나오는 결고를 discriminator에 넣었을 대 그 결과를 log(1-결과)했을 때 얻는 기댓값

이 방정식을 D의 입장, G의 입장에서 각각 이해해보면 -먼저 D의 입장에서 이 value function $V(D,G)$ 의 이상적인 결과를 생각해보면 D가 매우 뛰어난 성능으로 판별을 잘 해낸다고 했을때 D가 판별하려는 데이터가 실제 데이터에서 온 샘플일 경우에는 $D(x$ )가 1이 되어 첫번째 항은 0이 되어 사라지고 $G(z)$ 가 생성해낸 가짜 이미지를 구별해낼 수 있으므로 $D(G(z))$ 는 0이 되어 두번째 항은 $log(1-0) = log1 = 0$ 이 되어 전체 식 $V(D,G) = 0$ 이 된다. 즉 D의 입장에서 얻을 수 있는 이상적인 결과 ‘최대값’은 0임을 확인 할 수 있다.
그 다음 G의 입장에서 이 value function $V(D,G)$ 의 이상적인 결과를 생각해보면 $G$ 가 $D$ 가 구별 못할만큼 진짜와 같은 데이터를 잘 생성해낸다고 했을 때, 첫번째 항 $\mathbb{E}_{x \sim p{\text{data}}(x)}[\log D(x)]$ 은 $D$ 가 구별해내는 것에 대한 항으로 G의 성능에 의해 결정될 수 있는 항이 아니므로 패스하고 두번째 항 $\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z))]$ 을 살펴보면 $G$ 가 생성해낸 데이터는 $D$ 를 속일 수 있는 성능이라 가정했기 때문에 $D$ 가 $G$ 가 생성해낸 이미지를 가짜라고 인식하지 못하고 진짜라고 결정내버린다. 그러므로 $D(G(z)) = 1$ 이 되고 $log(1-1) =$ 마이너스 무한대가 된다. 즉 $G$ 의 입장에서 얻을 수 있는 이상적인 결과 ‘최솟값’은 마이너스 무한대 임을 확인할 수 있다.
다시 말해 D는 training data의 sample과 G의 sample에 진짜인지 가짜인지 올바른 라벨을 지정할 확률을 최대화하기 위해 학습하고 G는 log(1-D(G(z))를 최소화 ( D(G(z))를 최대화)하기 위해 학습되는 것
D 입장에서는 V(D,G)를 최대화시키려고 G입장에서는 V(D,G)를 최소화시키려고 하고 논문에서는 D와 G를 V(D, G)를 갖는 two-player min_max game으로 표현
또 학습시킬때 inner loop에서 $D$ 를 최적화하는 것을 많은 계산들을 필요로 하고 유한한 데이터셋에서는 overfitting을 초래함. 그래서 $k-step$ 만큼 D를 최적화하고 G는 $1 step$ 만큼 최적화하도록 한다. ((알고리즘으로 확인가능) 앞서 말했듯이 학습 초반에는 g의 성능이 형편없기 때문에 D가 G의 생성해낸 데이터와 실제 테이터 샘플을 너무 잘 구별해 버린다. 이런 경우에는 $log(1-D(G(z))$ 가 포화상태가 되므로 $log(1-D(G(z))$ 를 최소화하려고 하는 것보다 $log(D(G(z))$ 를 최대화되게끔 학습하는 것이 더 좋다. G가 형편없을 때에는 log(1-D(G(z))의 gradient를 계산했을 때 너무 작은 값이 나오므로 학습이 느리기 때문이다.

Figure 1

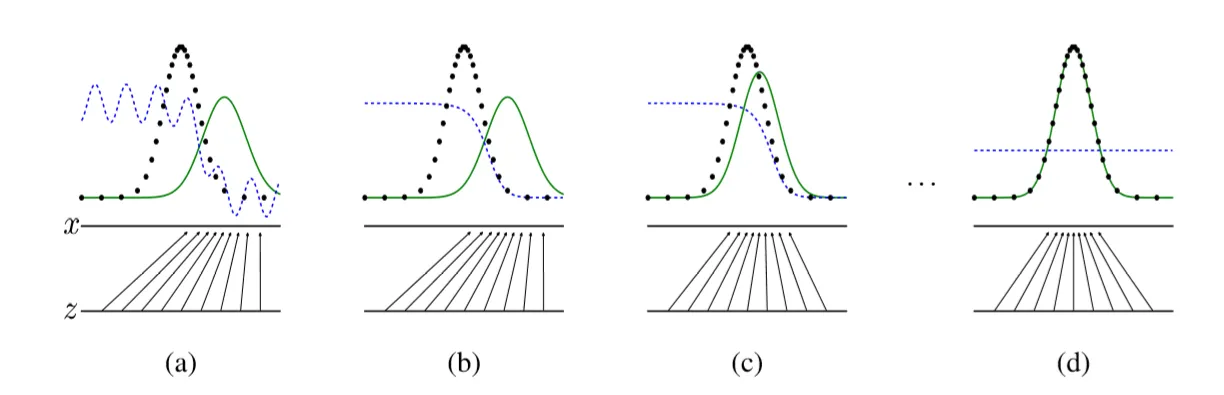
파란색 점선 : discriminative distribution
검은색 점선 : data generating distribution(real)
녹색 실선 : generative distribution(fake)

GAN의 학습과정은 이 그림을 통해 확인해보면

(a) 학습 초기 단계에서는 $Generator(G)$ 가 만들어내는 가짜 데이터의 분포 $p_g$ 와 실제 데이터의 분포 $p_{\text{data}}$ 가 명확히 다릅니다. 이 시점에서 $Discriminator(D)$ 는 가짜와 진짜를 잘 구분하지 못하며, 예측 확률도 들쭉날쭉합니다. 즉, $D$ 의 성능이 아직 충분히 올라오지 않은 상태입니다.

(b) 학습이 진행되며 D는 점차 진짜와 가짜 데이터를 구분하는 능력을 키웁니다. 이제 D는 흔들리지 않고 일관된 방식으로 분류를 수행하며, $D(x) ≈$ $\frac{p_{data(x)}}{p_{data}(x) + p_g(x)}$ 에 수렴합니다. 이는 D가 더 이상 랜덤하게 판단하지 않고, 신뢰할 수 있는 판별자로 작동하기 시작했음을 의미합니다.

(c) D가 어느 정도 학습된 이후에는 G가 D를 속이기 위해 실제 데이터 분포를 따라가는 방향으로 점차 학습됩니다. D의 gradient 정보를 활용해 G는 가짜 데이터를 실제처럼 보이도록 점점 개선하고, 그 결과 D는 점차 구분하기 어려워집니다.

(d) 이러한 경쟁이 반복되면서 G가 생성한 데이터의 분포 $p_g$ 는 실제 데이터 분포 $p_{\text{data}}$ 에 가까워집니다. 최종적으로 두 분포가 거의 일치하면, D는 더 이상 진짜와 가짜를 구분할 수 없게 되며, 모든 샘플에 대해 확률 $\frac{1}{2}$ 를 출력하게 됩니다.

→ 이 과정으로 진짜와 가짜 이미지를 구별할 수 없을 만한 데이터를 G가 생성해내고 이게 GAN의 최종 결과라고 볼 수 있다.

4 Theoretical Results

Generator $G$ 는 잠재 변수 $z∼p_z$ 를 입력받아 샘플 $G(z)$ 을 출력한다. 이 과정을 통해 G는 새로운 확률 분포 $p_g$ 를 암묵적으로 정의하게 된다. 즉, $p_g$ 는 $G(z)$ 로부터 샘플링된 데이터들의 분포이다.

충분한 모델 용량과 학습 시간이 주어진다면 $Algorithm 1$ (GAN 학습 알고리즘)이 진짜 데이터의 분포
$p_{data}$ 를 잘 근사하는 $p_g$ 로 수렴을 목표로 삼는다.

이 섹션에서의 분석은 모델의 용량을 무한대로 가정한 비모수(non-parametric) 설정에서 진행된다. 즉, 파라미터 수에 제한이 없는 경우를 가정하여 확률 밀도 함수의 공간에서 수렴(convergence)성질을 이론적으로 분석한다.

Section 4.1에서는 이 minimax 게임이 글로벌 최적점(global optimum)을 가지며, 그 지점에서 $p_g = p_{\text{data}}$ 임을 수학적으로 증명합니다.
Section 4.2에서는 $Algorithm 1$ 이 실제로 앞서 제시한 목적 함수 (즉, Equation 1)를 최적화한다는 것을 보여주어, 우리가 원하는 수렴 결과를 얻을 수 있음을 증명합니다.

Algorithm 1

Generator가 만드는 분포 $p_g$ 는 실제 데이터 분포 $p_{\text{data}}$ 와 같아진다.

즉 $p_g = p_{\text{data}}$ 가 GAN이 도달하는 global optimum임을 보이고자 합니다.

4.1 GlobalOptimality of $p_g=p_{data}$

표기 방식	의미	사용 목적
$\int_x p(x) f(x) dx$	기대값	수학적 엄밀성 강조
$\mathbb{E}_{x \sim p(x)}[f(x)]$	기대값	직관적, 코드/논문에서 자주 사용

E_{x∼p(x)} [f(x)]=∫_xp(x)f(x)dx

Proposition 1: 최적의 Discriminator

Generator G가 고정된 경우 Discriminator D를 V(G,D)에 대해 최적화하면 최적 형태는 다음과 같다.

D^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}

이것은 x가 진짜 데이터일 확률 비율에 해당하며 이는 실제로 Discriminator가 이상적으로 학습되었을 때 보여야 하는 출력 값이다.

목적 함수 $V(G, D)$

V(G, D) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z))]

V(G,D)=∫_xp_{data}(x)logD(x)dx+∫_zp_z(z)log(1−D(G(z)))dz

이 함수를 $D^*(x)$ 로 대체하여 $C(G) = max_DV(G,D)$ 를 구함

“여기서 왜 G(z)가 갑자기 x로 바뀌었지??

Generator $G(z)$ 가 생성한 샘플의 분포가 바로 $p_g$ 이기 때문이다.

$z \sim p_z$ 이고,

G(z) 를 통과한 결과 $x′=G(z)$ 는 $p_g$ 를 따름.

그러므로 $z∼p_z→G(z)∼p_g$

따라서 $E_z∼p_z[log⁡(1−D(G(z)))]$ 은 그냥 $E_x∼p_g[log⁡(1−D(x))]$ 으로 쓸 수 있다.

표기	의미	왜 바꿀 수 있나?
$G(z)$	noise $z$ 로부터 만들어진 가짜 샘플
$x∼p_g$	G가 만들어낸 샘플들의 분포	$G(z)∼p_g$ 이기 때문에
$z∼p_z→G(z)∼p_g$	즉, 샘플링 단계를 생략하고 분포로 바로 접근 가능

최종 목적 함수 C(G) 유도

C(G) = \mathbb{E}_{x \sim p_{\text{data}}} \left[ \log \left( \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right) \right]+ \mathbb{E}_{x \sim p_g} \left[ \log \left( \frac{p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right) \right]

C(G) = \max_D V(G, D) = \mathbb{E}_{x \sim p_{\text{data}}} [\log D^*_G(x)] + \mathbb{E}_{x \sim p_g} [\log(1 - D^*_G(x))]

Theorem 1 : $p_g = p_{data}$ 일 때 최솟값을 달성함

만약 $p_g = p_{data}$ 라면 $D^*(x) = \frac{1}{2},$ $log D^*(x) = log(1/2) = - log2$ $C(G)=\mathbb{E}[−log2]+\mathbb{E}[−log2]=−log4$

Kullback–Leibler (KL) 및 Jensen-Shannon Divergence (JSD)

C(G)=−log(4)+2⋅JSD(p_{data}∥p_g)

JSD는 두 분포가 같을 때만 0이므로, C(G)의 최소 값은 오직 :

p_g=p_{data}⇒JSD=0⇒C(G)=−log4

GAN이 수렴한 최종 상태는 $p_g = p_{\text{data}}$ 일 때이며,
이 경우, Discriminator는 어떤 샘플이 진짜인지 구별할 수 없고 항상 0.5를 출력하게 된다.
따라서 Generator는 진짜와 구분되지 않는 데이터를 생성하게 되는 것.

what is KL, JSD?

“분명히 $C(G)=log(1/4)=−log4$ 가 GAN의 수렴 지점이라고 했는데, 갑자기 JSD가 왜 등장하고 KL도 왜 나오는 거야?"라는 의문점이 떠올랐다.

1. 수렴지점 “ $C(G) = -log4$ ”

Generator $G$ 가 실제 데이터 분포를 완벽히 모방할 경우 $p_g = p_{data}$
이때 최적 Discriminator $D^*(x) = \frac{1}{2}$
따라서 목적 함수 $C(G)$ 는 :

C(G) = log\frac{1}{2} + log\frac{1}{2} = - log4

여기가 끝이 아니라

2. C(G)는 다른 분포에서도 정의된다.

논문이 여기서 한 발 더 나아간 이유는 :

$p_g \ne p_{data}$ 인 경우에도 C(G)가 어떤 값을 갖는지 알고 싶어서다.

C(G)가 어떻게 변하면서 수렴하는지 볼 수 있고,

C(G) “두 분포 사이의 거리"처럼 작동한다는 걸 정량적으로 보여줄 수 있음.

3. 그래서 등장한 게 KL, JSD

C(G) = -\log 4 + KL\left(p_{\text{data}} \, \bigg\| \, \frac{p_{\text{data}} + p_g}{2} \right) + KL\left(p_g \, \bigg\| \, \frac{p_{\text{data}} + p_g}{2} \right)

이걸 보면 두 개의 KL divergence가 나와. 이걸 모아서 만든 게 바로:

\mathrm{JSD}(p_{\text{data}} \,\|\, p_g) =\frac{1}{2} \, \mathrm{KL}(p_{\text{data}} \,\|\, M) +\frac{1}{2} \, \mathrm{KL}(p_g \,\|\, M), \quad\text{where } M = \frac{p_{\text{data}} + p_g}{2}

즉,

C(G)=−log4+2⋅JSD(p_{data}∥p_g)

4. 이게 왜 중요한가?

이제 이론적으로 말할 수 있다.

$p_g = p_{data}$ 이면 $JSD = 0$ ⇒ $C(G) = -log4$
$p_g \ne p_{data}$ 이면 $JSD > 0$ ⇒ $C(G) > -log4$

GAN이 학습되면서 $C(G)↓$ 하는 것은,

$\text{JSD}(p_{\text{data}} \Vert p_g) \downarrow$ 한다는 뜻이며,

$p_g \to p_{\text{data}}$ 에 가까워지고 있다는 것을 수학적으로 보장해주는 장치이다.

개념	설명
$C(G)=−log⁡4$	수렴 시점의 최솟값
JSD 추가	두 분포가 얼마나 다른지를 측정하는 방식
수식화	$C(G)=−log⁡4+2⋅JSD(p_{data}∥p_g)$
의미	GAN 학습이 수렴하는 정도를 정량적으로 분석 가능하게 해줌

4.2 Convergence of Algorithm 1

GAN의 수렴 보장

논문의 4.2절은 GAN의 학습이 실제 데이터 분포 $p_{data}$ 로 수렴할 수 있다는 이론적 조건을 설명한다. 여기서 중요한 가정은 2가지 이다.

Generator $G$ 와 Discriminator $D$ 가 충분한 표현력을 가진다는 것
Discriminator는 각 학습 스텝마다 주어진 $G$ 에 대해 항상 최적 $D^*_G$ 에 도달한다는 것

이러한 조건 속에서 Generator가 $D^*_G$ 의 출력을 기반으로 조금씩 $p_g$ 를 개선해 나가면 결국 Generator가 만드는 분포 $p_g$ 는 실제 데이터 분포 $p_{data}$ 에 수렴하게 된다.

Proof (수학적 직관)

이 증명은 목적함수 $V(G, D)$ 를 고정된 $D^*$ 하에서 Generator 분포 $p_g$ 에 대한 함수 $U(p_g, D)$ 로 보는 데서 시작된다.

이때 중요한 사실은 이 함수 $U(p_g, D)$ 가 $p_g$ 에 대해 convex(볼록)하다는 점이다.

볼록 함수들의 상한값들(supremum)을 취한 함수의 서브그래디언트는 최댓값을 이루는 지점에서의 그래디언트를 포함한다는 성질을 사용하면 이것은 $p_g$ 에 대한 gradient descent 업데이트가 가능한 상황과 같게 된다.

따라서 Discriminator가 항상 최적인 상태에서 Generaotr가 조금씩만 개선된다면 $p_g$ 는 결국 $p_{data}$ 에 수렴하게 된다는 결론에 도달한다.

In practice (실제 구현과의 차이)

하지만 현실의 GAN 구현에서는 $p_g$ 라는 분포를 직접 다루지 않고 Generator는 $z \sim p_z$ 라는 노이즈를 받아 신경망 $G(z; \theta_g)$ 형태로 이미지를 생성한다.

즉, 실제로 $\theta_g$ 라는 모델 파라미터를 최적화하는 방식이다.

이런 구조는 이론과는 달리 parameter space에 여러 개의 local minima나 sddle point 같은 복잡한 최적화 문제가 발생 할 수 있다.

그럼에도 불구하고 다층 퍼셉트론 기반의 Generator는 실제 실험에서는 좋은 성능을 보여주며 엄밀한 이론적 보장이 없더라도 충분히 실용적인 모델이라는 점이 강조된다.

5. Experiments

GAN의 성능을 검증하기 위해 MNIST, TFD(Toronto Face Database), CIFAR-10 세 가지 데이터셋에서 실험을 진행했다. Generator 네트워크에는 ReLU와 sigmoid를 혼합해 사용했고 Discriminaotr는 maxout activation과 dropout을 사용했다. Generator에는 오직 입력층에만 noise를 추가했다.

학습이 완료된 후에는, Generator가 생성한 샘플 분포 $p_g$ 에 대해 Parzen window 기반 Gaussian 밀도 추정을 사용해 test set 샘플의 log-likelihood를 추정했다. 이 추정 방법은 정확한 likelihood를 계산할 수 없는 모델에 대해 자주 사용되는 방법이며 모델의 샘플링 성능을 간접적으로 평가한다.

→ 결과: G가 생성해낸 sample이 기존 존재 방법으로 만든 sample보다 좋다고 주장할 수 는 없지만, 더 나은 생성모델과 경쟁할 수 있다 생각하며, adversarial framework의 잠재력 강조함.

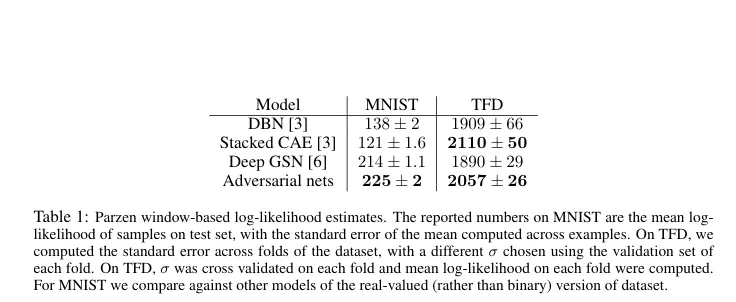
MNIST 실험에서는 GAN이 가장 높은 log-likelihood (225±2)를 기록하여 기존 모델보다 우수한 샘플링 품질을 보였다.
TFD에서는 Stacked CAE가 가장 높은 점수를 얻었지만 GAN 역시 Deep GSN이나 DBN보다 높은 성능을 기록했다.
참고로 이 방법은 고차원 공간에서는 분산이 크고 정확도가 떨어질 수 있는 평가 방식임에도 불구하고 GAN이 경쟁력 있는 결과를 보였다는 점이 강조

Figure 2

Figure 2는 훈련 후 Generator가 생성한 샘플을 보여준다. 샘플은 다음과 같은 네 가지 경우에 대해 제시된다.

(a) MNIST
(b) TFD
(c) CIFAR-10 (fully connected 구조)
(d) CIFAR-10 (conv discriminator + deconv generator)

→ 샘플은 임의로 뽑힌 것이며, cherry-picking 없이 모델의 실제 출력이다.

→오른쪽 열에는 가장 유사한 학습 데이터를 함께 보여주며, 모델이 단순 암기한 것이 아님을 검증하고 있다.

→ Markov chain에 의존하지 않기 때문에 샘플 간 상관이 없고 진짜로 생성된 데이터라는 점도 강조된다.

Figure 3

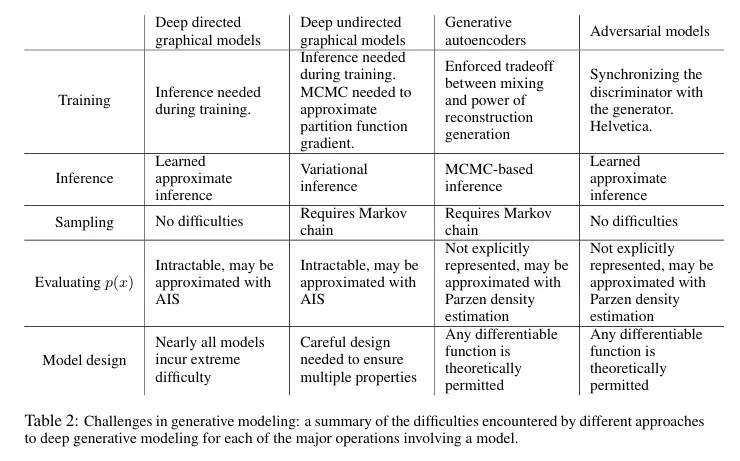
Table 2 - Deep generative 모델들의 공통적인 어려움 비교

6 Advantages and disadvantages

단점
- $p_g(x)$ 가 명시적으로 존재하지 않음
- D와 G가 균형을 잘 맞춰 성능이 향상되어야 함(G는 D가 너무 발전하기 전에 너무 발전되어서는 안된다. G가 z 데이터를 너무 많이 붕괴시켜버리기 때문)
장점
- Markov chains이 젆 필요 없고 grdients를 얻기 위해 backpropagation만이 사용됨
- 학습 중 어떠한 inference가 필요없음
- 다양한 함수들이 모델이 접목될 수 있음
- Markov chains을 쓸 때보다 훨씬 선명한 이미지를 얻을 수 잇음

7.Conclustions and future work

conditional generative model로 발전시킬 수 있음 (CGAN)
Learned approximate inference는 주어진 x를 예측하여 수행될 수 있음
parameters를 공유하는 conditionals model를 학습함으로써 다른 conditionals models을 근사적으로 모델링할 수 있음. 특히 MP-DBM의 stochastic extension의 구현 에 대부분의 네트워크를 사용할 수 있음
Semi-supervised learning: 제한된 레이블이 있는 데이터 사용할 수 있을 때, classifiers의 성능 향상시킬 수 있음
효율성 개선: $G$ , $D$ 를 조정하는 더 나은 방법이나 학습하는 동안 sample z에 대한 더 나은 분포를 결정함으로써 학습의 속도 높일 수 있음

참고한 것들

홍선재

이전 포스트

Generative Adversarial Nets (GAN)

국민대학교 인공지능학회 (XAI)

Abstract

1. Introduction