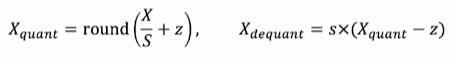모델 최적화와 경량화: Quantization

1. Quantization(양자화)

• 숫자의 정밀도(precision)을 낮추는 최적화 및 경량화 기법

  • 정밀도?
    의도한 숫자를 얼마나 정확하게 표현할 수 있는지
    • 3.141592
      3.14

      그럼 언제나 정밀도가 높은것이 좋느냐?
      아니다. 낮은 정밀도는 오차가 발생하나 계산속도가 향상되고 메모리 사용량도 줄어든다.
      그래서 Quantization의 최대 목표는 오차를 최소화 하는 낮은 정밀도 표현을 찾는 것이다.
      

• Quantization의 에러가 커질수록 성능 저하

  • 잠재적 이유
    • 누적오차
      작은 오차들이 층을 거치면서 누적되고 증폭
    • 뉴런 비활성화
      작은 양수를 음수로 오변한 후 ReLU함수는 뉴런을 비활성화

2. Model Quantization

2.1 Quantization Mapping

• 높은 정밀도 데이터를 낮은 prevision으로 대응시키는 quantization 계산식을 지칭
  • Example
    FP32 데이터를 INT8로 대응
• 이는 대상이 되는 데이터, 파라미터 묶음 마다 각각 존재
  • 데이터의 경우, 전체 데이터 단위로 mapping을 생성
    • 데이터 mapping
      • FP32로 표현된 350.5, 1.5, -350.5를 INT8로 표현하려면?
    • 파라미터의 경우, 일반적으로 레이어 단위로 mapping을 생성
      파라미터 mapping

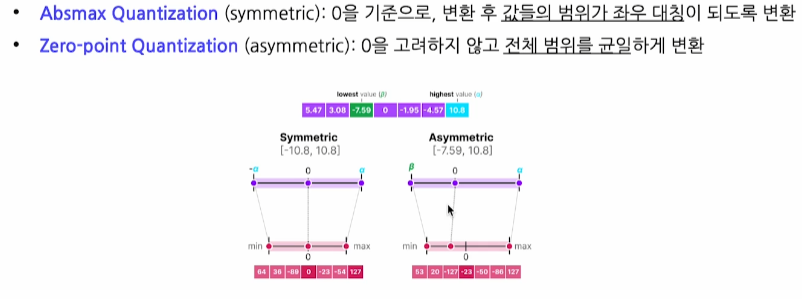
• Absmax Quantization
  0을 항상 0으로 보내는 것이 효과적인 경우에 활용한다.
  • Tanh는 -1 에서 +1 사이의 대칭적인 분포를 가짐
• Zero-point Quantization
  데이터 분포가 비대칭적이거나 평균 값이 0이 아닌 경우
  • RelU의 경우, 양수 값만 사용하기 떄문에, 이 방법이 더 오차가 적다.

Quantization Parameters

• 어떤 값들을 실제로 저장해야 할까?
  양자화된 값들을 저장하고 이를 복원(역양자화)하는 방식으로 사용

1. 양자화 방식
   어떠한 방식을 활용했는지 등의 메타데이터

2. Quantized value
   양자화를 거쳐서 나온 실제 값

3. Scale factor(s)
   기울기 값

4. Zero-point(z)
   0의 양자화 후 위치

• 수식
  

2.2 Absmax Qauntization

• s와 z만 구하면 모든 값 양자화/역양자화 가능
  

• 데이터에서 절대값의 최대값(absmax) 계산(기준값)

  • 기준값 x 2가 변환 후 -127 ~ 127이 되도록 scaling
    

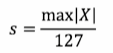
  • 비율대로 다른 값들을 INT8 내에서 조정

• Absmax의 경우 대칭방식이라 zero-point는 항상 0!
  z = 0
  

• 양자화된 데이터가 부동소수 없이 모두 정수로 저장되어 있음을 볼 수 있다.

• Dequantize 계산
  

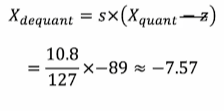
• 복원 후 데이터
  
  
  

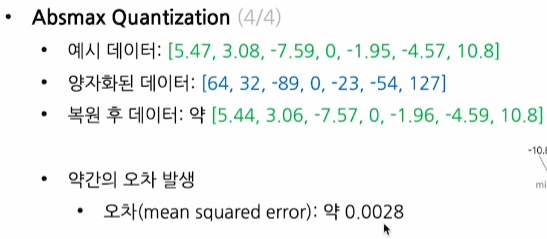
양자화된 데이터는 IN8로 저장하지만,
Scale factor Zero-point의 경우에는 높은 정밀도로 저장한다. 어차피 공간 얼마 차지 안하니까!복원용도인 둘은 높은 정밀도로 저장하는게 좋다!

2.3 Zero-point Quantization

• 데이터에서 최대값이 127, 최솟값이 128이 되도록
  • Scale factor와 zeropoint 계산
    
    
    
    
    

저장해야할 값은

• Scale factor:s
• Zero-point: z

absmax 같은 경우에는 어차피 0이라 zero-point를 저장하지 않는다.

• 비교(Absmax VS Zero-point

Mapping	기준값	대칭성	주 용도	한계
Absmax Quantization	절대값의 최대값	대칭	0이 중요한 경우	극단적인 값에 예민
Zero-point Quantization	최대-최소의 차이	비대칭	비대칭 분포인 경우	기준점(0점)이 비정상적일 경우 성능이 떨어질 수 있음

극단적인 값에 예민할 때에는 어떻게 해야하는가?

Clipping

2.4 Clipping

• 극단적인 outlier 값의 영향을 줄이기 위한 기술

• 일정 범주를 넘어가면 같은 값으로 취급하기
  

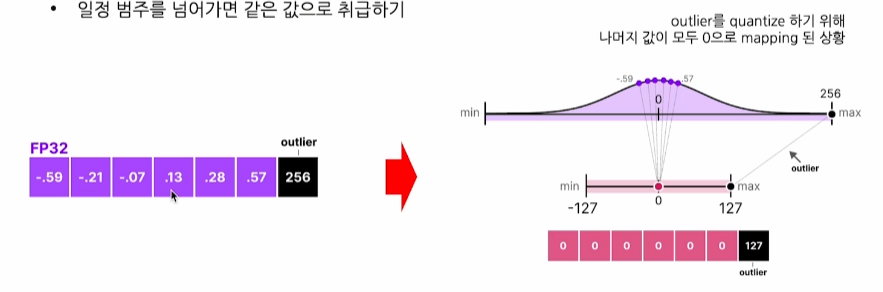
• 가령 범주를 [-5, 5]라고 지정했다면, 256 같은 값을 5로 바꾼 후에 quantize 진행

  • 256 > 5? --> 5

• 이 좋은 범주(range)를 찾는 과정을 calibration이라고 함

3. 요약

• Quantization
  높은 정밀도 숫자를 낮은 정밀도 숫자로 변환
  • 예) FP32를 INT8로 변환
  • 메모리 및 저장공간 효율, 연산 속도 향상
  • Quantization Mapping
    • Absmax(symmetric)
    • Zero-point(asymmetric)
    • Clipping