✔ 최단 경로 알고리즘으로 주어진 노드와 간선들 중 가장 짧은 경로를 찾는 알고리즘이다.
📌shortest path algorithm
- dij : i에서 j까지 부여된 간선의 가중치, 두 라우터 i와j 사이의 거리를 의미한다.
- p(path) : dij + djk + dkn..+ dlm 으로 직접 연결된 경로를 의미한다. 가장 작은 길이의 path를 찾는 것이 바로 최단경로 탐색 알고리즘이다. 최단경로 알고리즘으로 Bellman-Ford, DAG, Dijkstara Floyd 알고리즘이 있다.
📌Bellman-Ford algorithm
- 한 정점에서 출발하여, 다른 모든 정점에 대한 최단경로를 구하는 알고리즘이고 음수 간선을 포함해도 계산할 수 있다.
- 최단 거리가 업데이트 되는 노드가 없어질 때 까지 계속해서 반복하여 구해주고, 음의 가중치로 인해 업데이트를 무한히 하게 되는 경우 탈출 시켜주어야 한다.(무한히 반복할 때는 최단거리가 없다고 한다.)
💡동작원리
- 음의 사이클이 없고 정점이 V개인 그래프에서, 한 정점에서 출발한 다른 정점까지의 최단경로는 많아봐야 V-1개의 간선을 지난다. 즉, 한 번 지난 정점은 다시 지나지 않는다. 따라서, 모든 정점에 대해 V-1번의 반복을 통해 가능한 모든 경로를 탐색하여 정확한 답을 내도록 한다.
- 만약 그래프에 그려진 간선이 없다면 dij = ∞로 만든다.
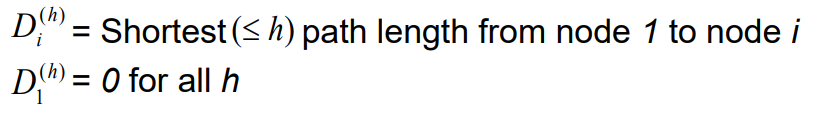
처음 Iteration를 1번 노드로 시작했다면 이후의 Iteration에서는, 다른 노드를 순서대로 시작점으로 두고 최단거리를 갱신한다.
📌Dijkstra’s algorithm
- 음의 가중치가 없는 그래프의 한 정점(Vertex)에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘이다.
💡 동작원리
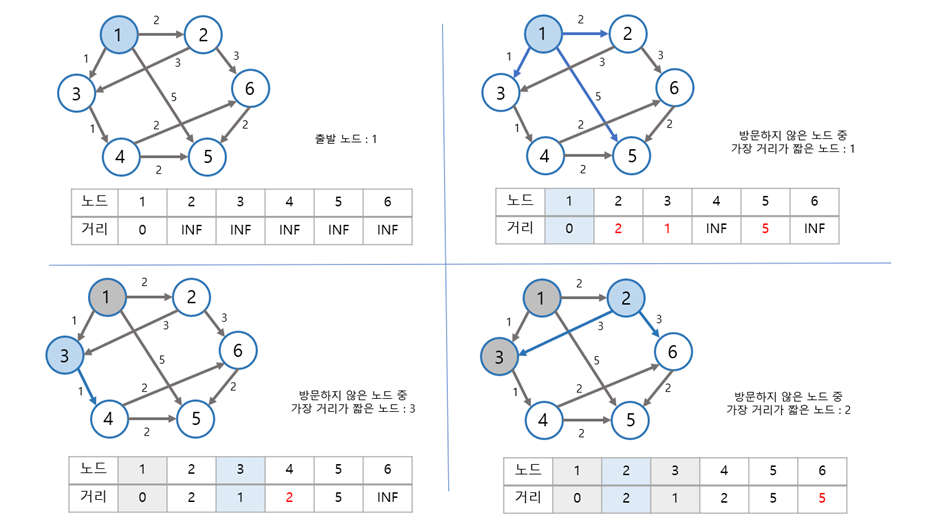
① 출발 노드와 도착 노드를 설정한다.
② '최단 거리 테이블'을 초기화한다.
③ 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고, 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택한다. 그 노드를 방문 처리한다.
④ 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트한다.
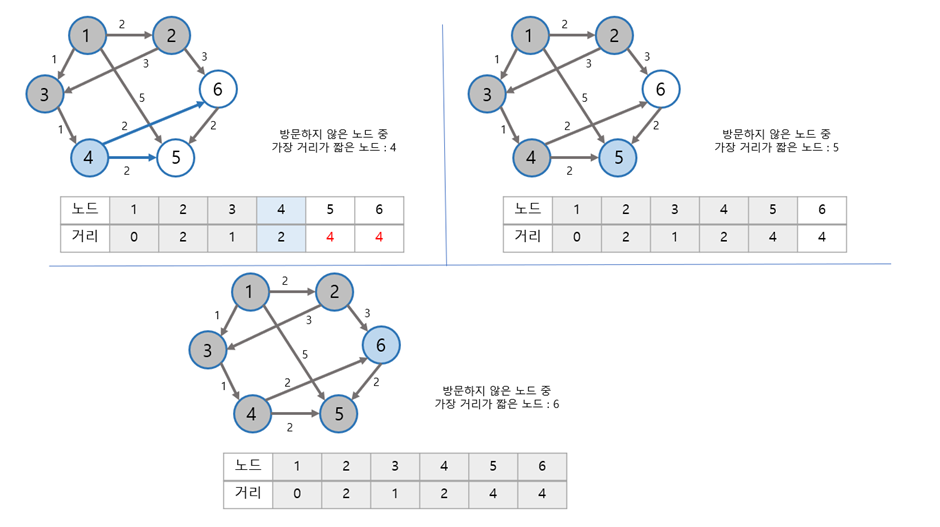
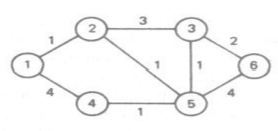
📌 Floyd-Warshall algorithm
- 플로이드-워셜 알고리즘은 한 번 실행하여 모든 노드 간 최단 경로를 구할 수 있다.
💡동작원리
-모든 노드 간의 최단거리를 구해야 하므로 2차원 인접 행렬을 구성하고 알고리즘은 여러 라운드로 구성된다. 라운드마다 각 경로에서 새로운 중간 노드로 사용할 수 있는 노드를 선택하고, 더 짧은 길이를 선택하여 줄이는 과정을 반복한다.
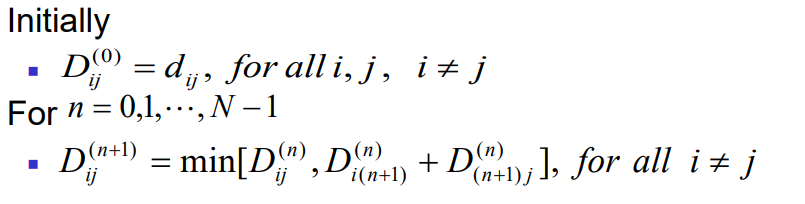
📌 Shortest path 적용한 예시
💡 벨만포드
💡 다익스트라
💡 플로이드-워셜
전공 소개