심층 L-레이어 신경망

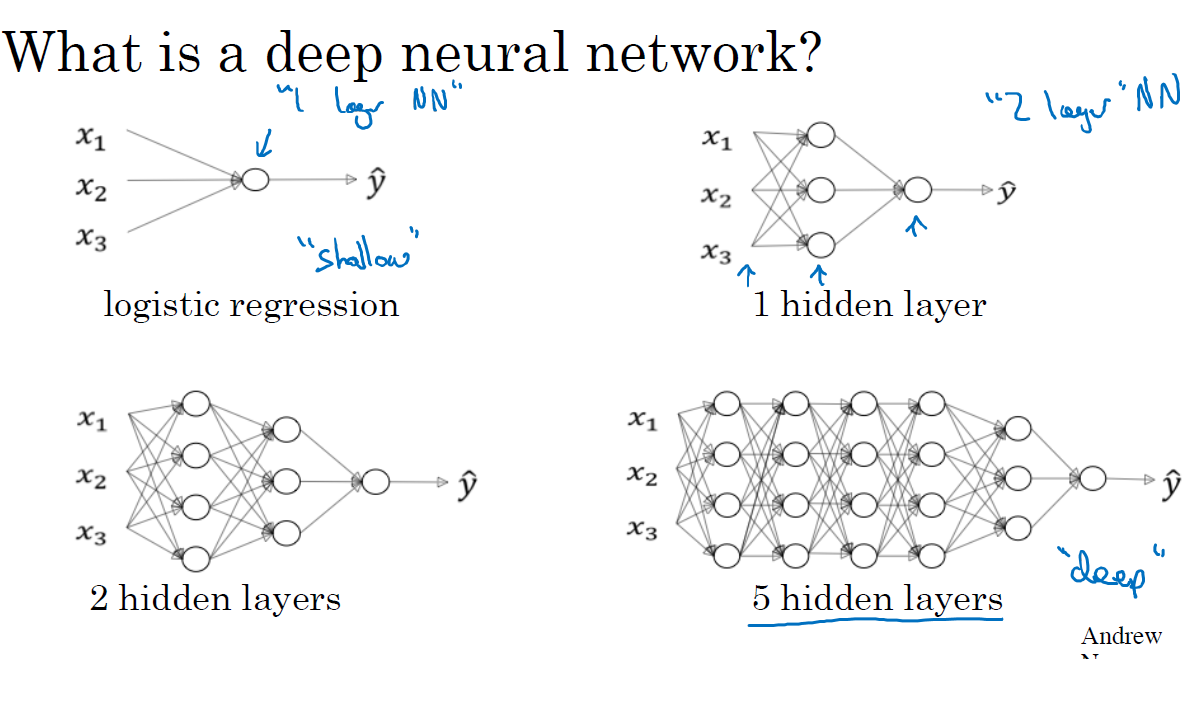
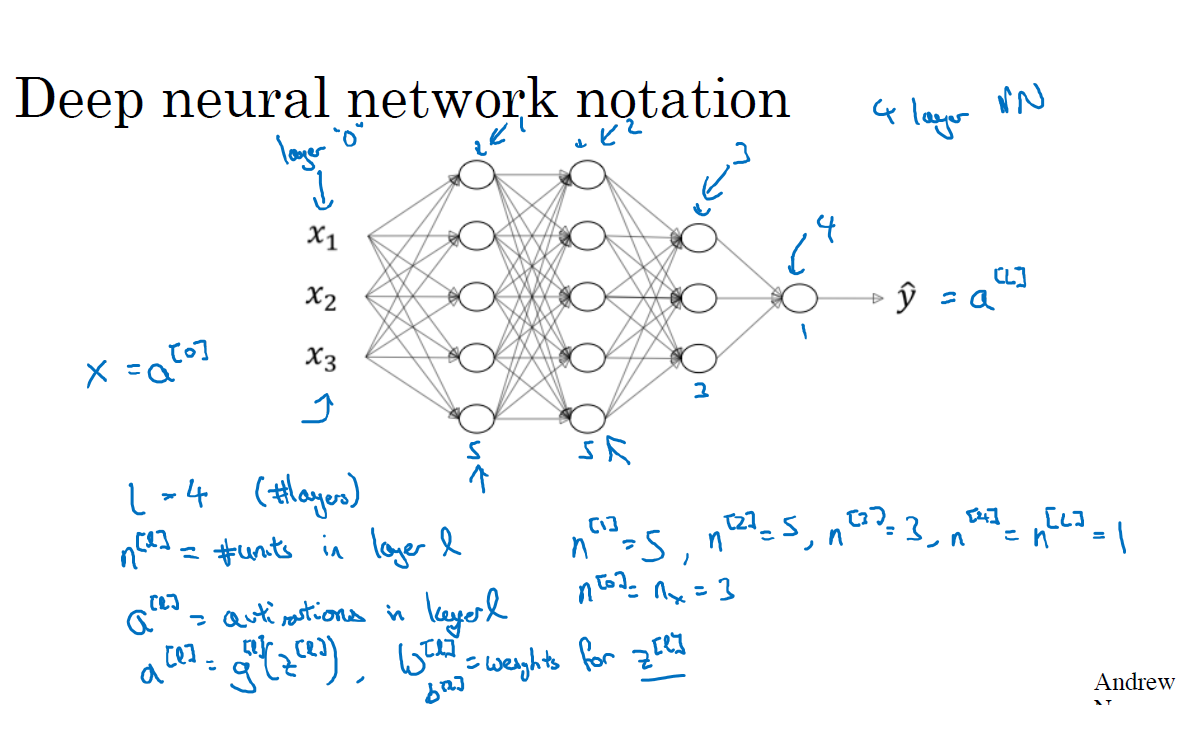
L => layers
$N^{[L]}$ => units layers
$N^{[0]}$ = $n_x$ => 입력층을 말함
$a^{[l]}$ => 활성화 layers를 나타냄 (활성화함수인가?)
$a^{[l]}=g^{[l]}(z^{[l]})$ => g는 활성화함수
$w^{[l]}$ => $z^{[l]}$을 위한 가중치
$X=a^{[0]}$ => 입력층
$\hat{y}=a^{[L]}$ => 출력층

딥 네트워크의 순방향 전파

레이어별 forward propagation
$z^{[1]} = w^{[1]}x + b^{[1]}$
$a^{[1]} = g^{[1]}(z^{[1]})$
$z^{[2]} = w^{[2]}a^{[2]} + b^{[2]}$
$a^{[2]} = g^{[2]}(z^{[2]})$
......
$z^{[4]} = w^{[4]}a^{[3]} + b^{[4]}$
$a^{[4]} = g^{[4]}(z^{[4]})$

forward propagation 공식 x는 $a^{[l-1]}$로 대체 가능하며 2번째 층부터는 $a^{[l-1]}$이다.
$z^{[l]} = w^{[l]}x + b^{[l]}$
$a^{[l]} = g^{[l]}(z^{[l]})$

Vectorization (벡터화되면 대문자 사용)
아래 과정이 반복된다.
$Z^{[1]} = W^{[1]}X + b^{[1]}$
$A^{[1]} = g^{[1]}(Z^{[1]})$
$Z^{[2]} = W^{[2]}A^{[2]} + b^{[2]}$
$A^{[2]} = g^{[2]}(Z^{[2]})$

Vectorization forward propagation 공식
$Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}$
$A^{[l]} = g^{[l]}(Z^{[l]})$

모든 훈련 예제는 왼쪽에서 오른쪽으로 열 벡터스택

올바른 매트릭스 크기 설정하기

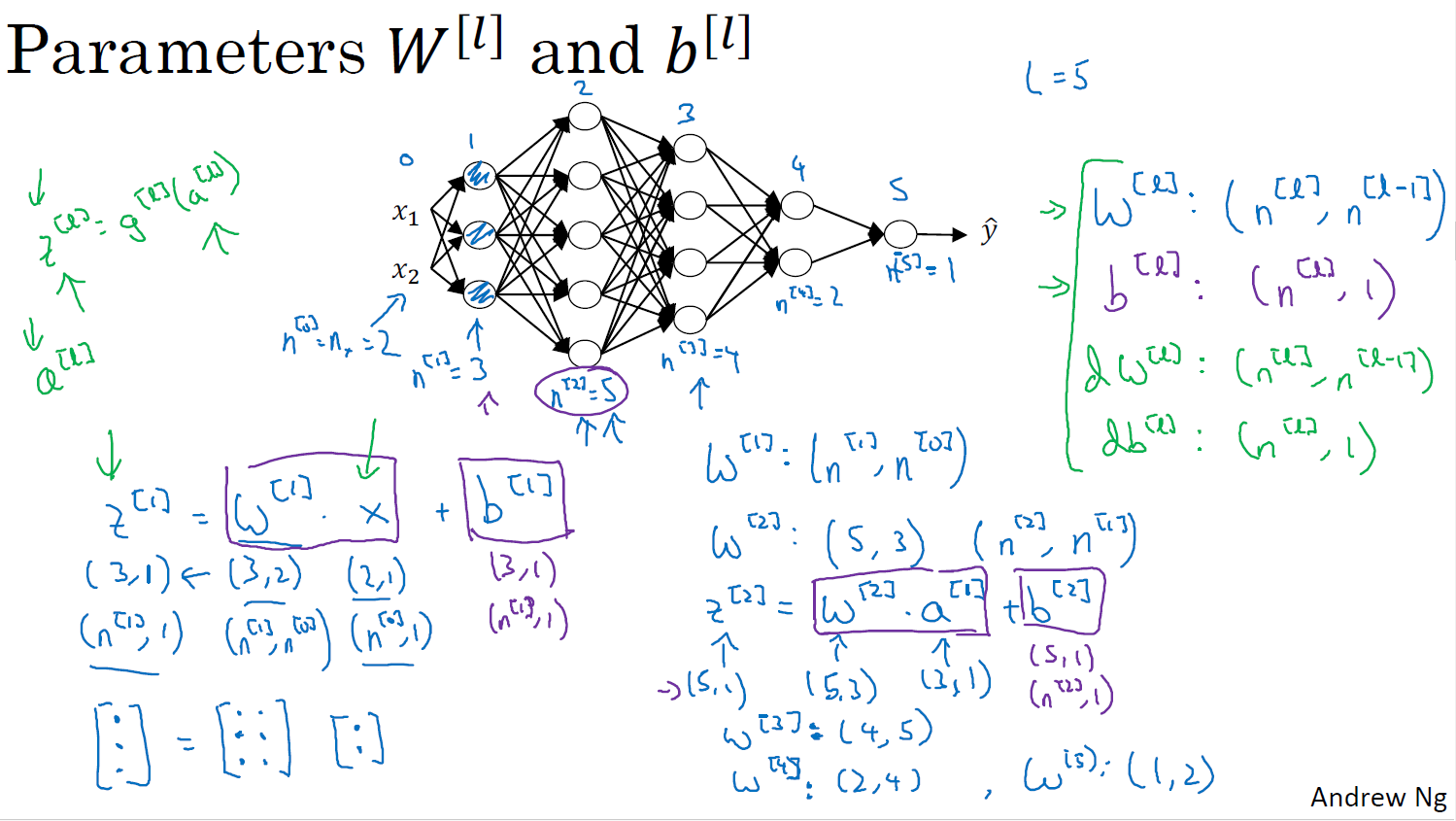
행렬의 공식? 같은거
$w^{[l]}: (n^{[l]}, n^{[l-1]})$
$b^{[l]}: (n^{[l]}, 1)$
$dw^{[l]}: (n^{[l]}, n^{[l-1]})$
$db^{[l]}: (n^{[l]}, 1)$

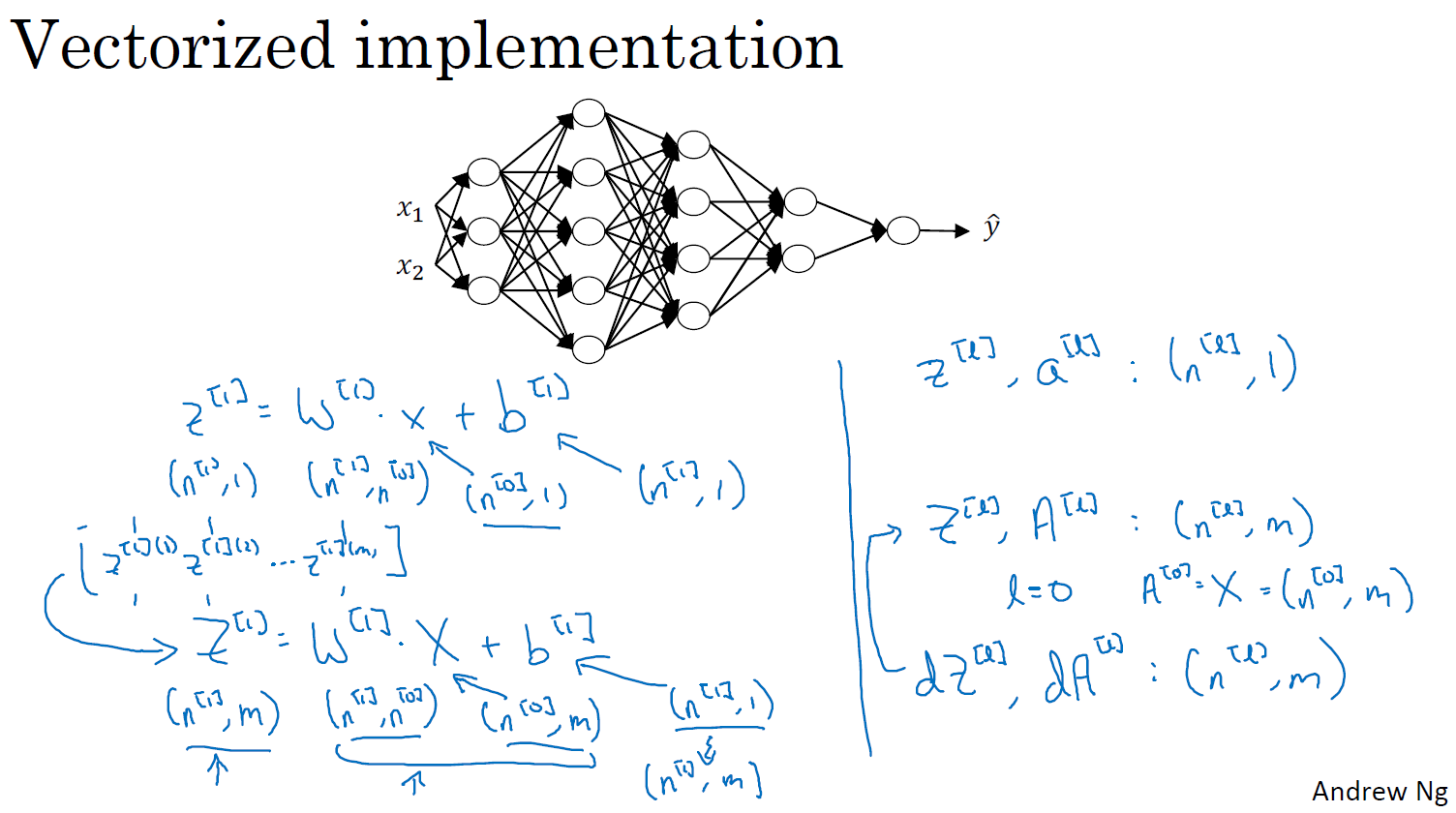
벡터화했을 떄
$z^{[l]}, a^{[l]} : (n^{[l]}, 1)$
$Z^{[l]}, A^{[l]} : (n^{[l]}, m)$
$l=0 A^{[0]} = X = (n^{[0]}, m)$
$dZ^{[l]}, dA^{[l]} : (n^{[l]}, m)$

심층 표현이 필요한 이유는?

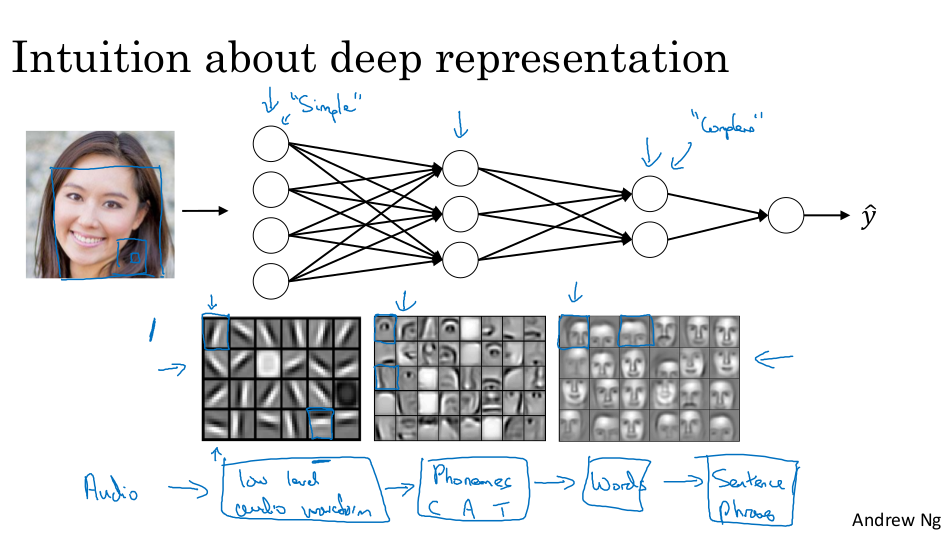
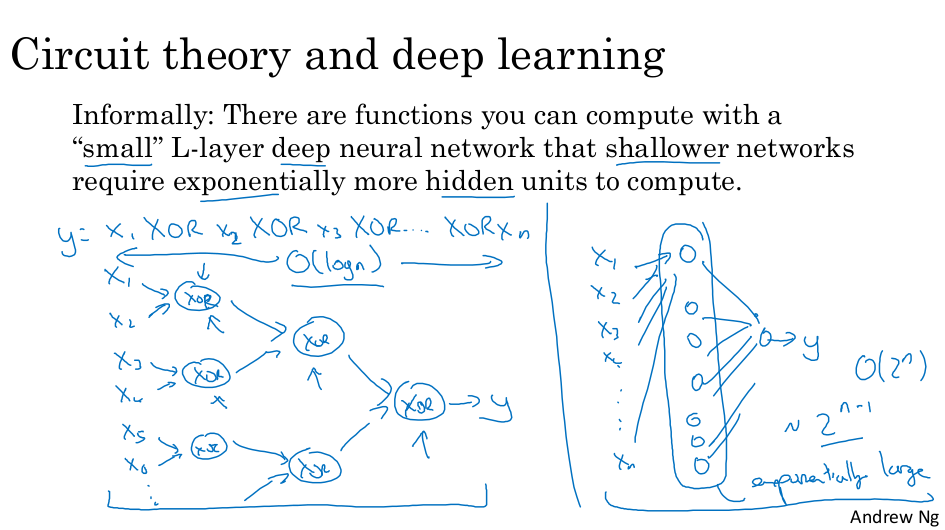
심층 신경망의 빌딩 블록

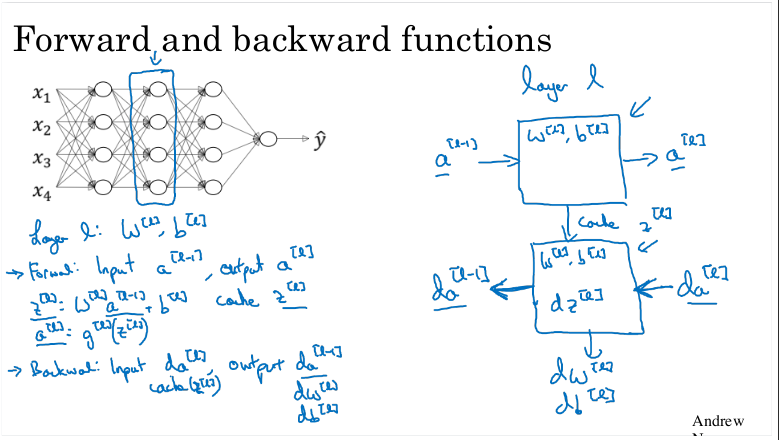
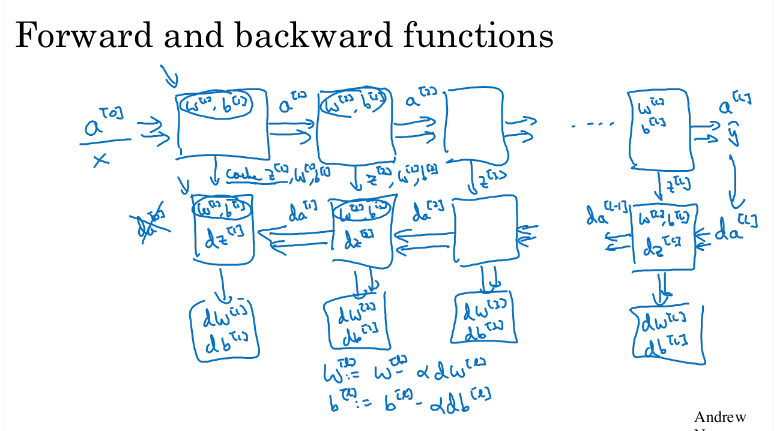
순방향 및 역방향 전파

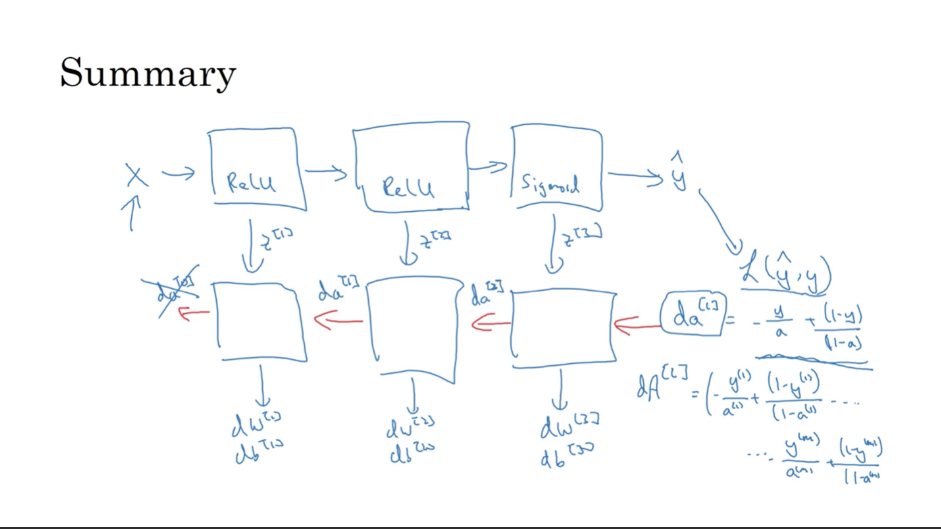
매개변수 대 하이퍼파라미터

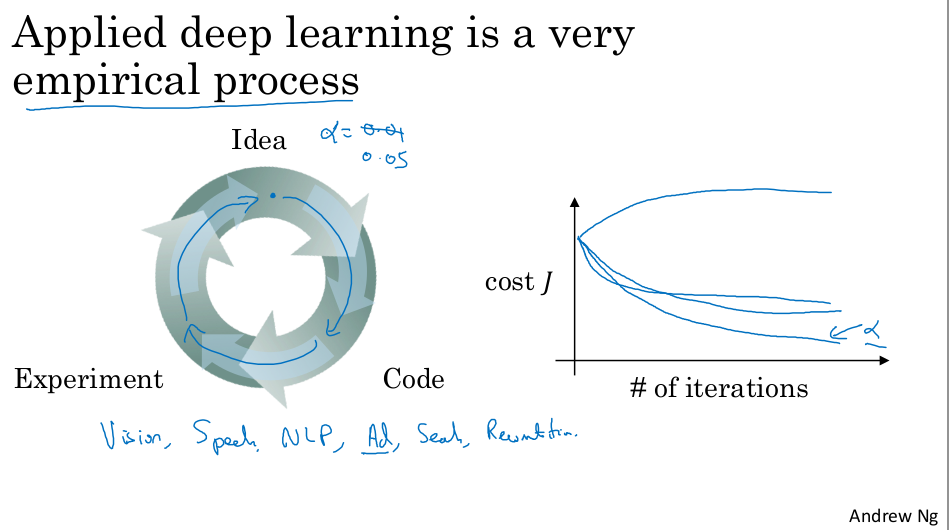
이것이 뇌와 어떤 관련이 있을까요?