Horizon Effect
고립게임에서 고려해야 할 특수 사항이 존재한다. 밑의 그림을 예시로 보자.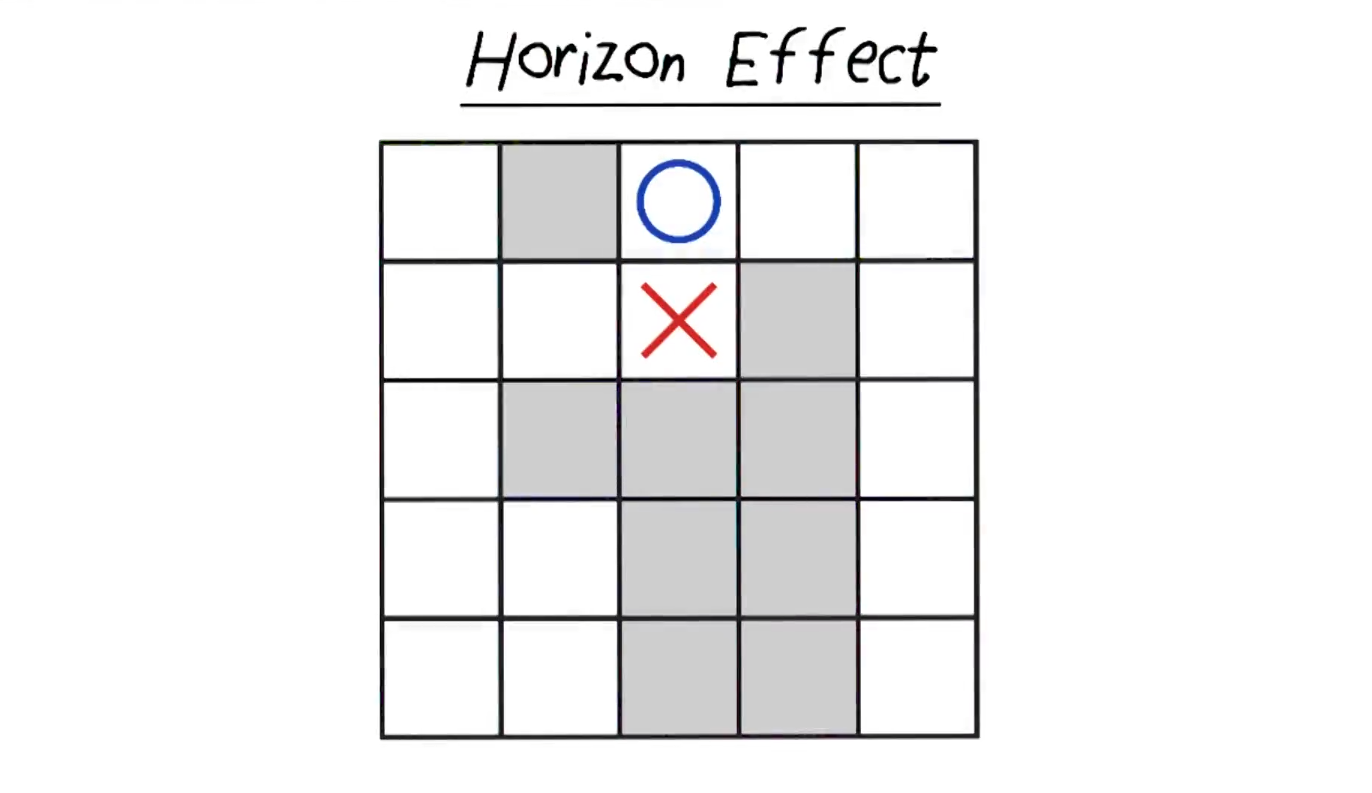
동그라미의 턴이라고 가정했을때, 어디로 움직이는 것이 승리의 결과값을 줄 수 있을까? 오른쪽으로 이동을 한다면 O에게 주어진 남은 칸의 갯수는 5개, 왼쪽 아래로 이동했을 경우에는 7개의 칸이 남기에 무조건 왼쪽아래로 이기는 것이 이득이다. 우리는 남은 칸의 갯수를 보면 바로 알 수 있지만, 기존의 틀에서 밖에 계산하지 못하는 컴퓨터의 경우 이 결과를 도출해 내기 위해선 총 7개의 깊이까지 가야만 왼쪽 아래로 가는 것이 더 이득이라는 결과를 나타낼 수 있다. 이렇게 보드를 반으로 갈라서 사용하는 상황을 강의에서는 "Horizon Effect" 라고 정의한다. 이런 HE를 마주했을때 남은 칸의 갯수를 새면 되지않느냐? 라고 강의자가 제시를 했지만 이러한 방법은 생각보다 리소스를 많이 잡아먹고, 다양한 경우의 수가 생길 수록 기하급수적으로 계산량이 많아진다고 얘기를 했다. 그렇기 때문에 우리는 조금 더 "똑똑한" / "최적화된" evaluation function이 필요한 경우들이 있다고 한다.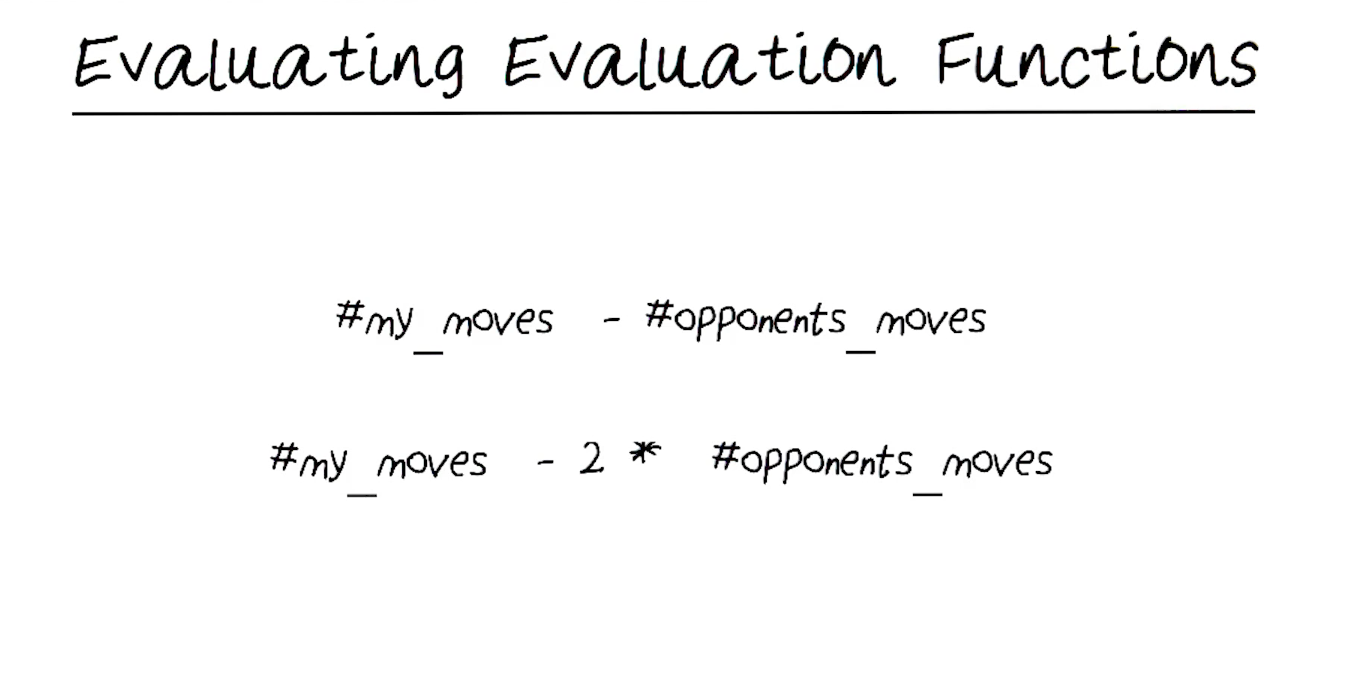
위의 계산식이 사실 우리가 원하는 evaluation function에 가장 적합하다고 한다. 결국 AI플레이어가 원하는 것은, 내가 갈 수 있는 경우의 수를 최대화하고 상대가 가능한 움직임의 경우의 수를 최소화하는 것이 목적이기 때문에 이 evaluation function은 굉장히 직관적이고 효율적이다. 다만 여기서 opponent move를 2로 곱했을 경우, 우리의 AI 플레이어가 훨씬 더 공격적으로 (상대방의 말을 더 적극적으로 따라다니며 상대방의 움직일 수 있는 경우의 수 들을 더 많이 차단) 움직인다고 한다. 이렇게 앞에 곱해주는 숫자나, 기존 evaluation function에서 조금 variation을 주게 되면 주어진 상황마다 더 최적화된 움직임을 취한다고 설명한다. 특히나 위에서 언급했던 horizon effect가 생겼을 경우 곱하기 2, 혹은 3값을 할 경우 이기는 경우의 수 (왼쪽 아래) 로 움직이는 수를 택한다고 한다. 그리고 이 계산량은 남은 칸의 갯수를 새는 것 보다 훨씬 더 적다!
Alpha-Beta Pruning (알파-베타 가지치기) 알고리즘
생각보다 시간이 지체되서 이 알고리즘은 다음 주차에 작성하도록 하겠다. 알파베타 프루닝 알고리즘은 계산량을 획기적으로 줄여주는 알고리즘으로 이러한 게임 풀이 AI에선 굉장히 중요한 개념이니, 다음 주차가 아마 제일 중요한 주차가 아닐까 싶다.
