인공지능

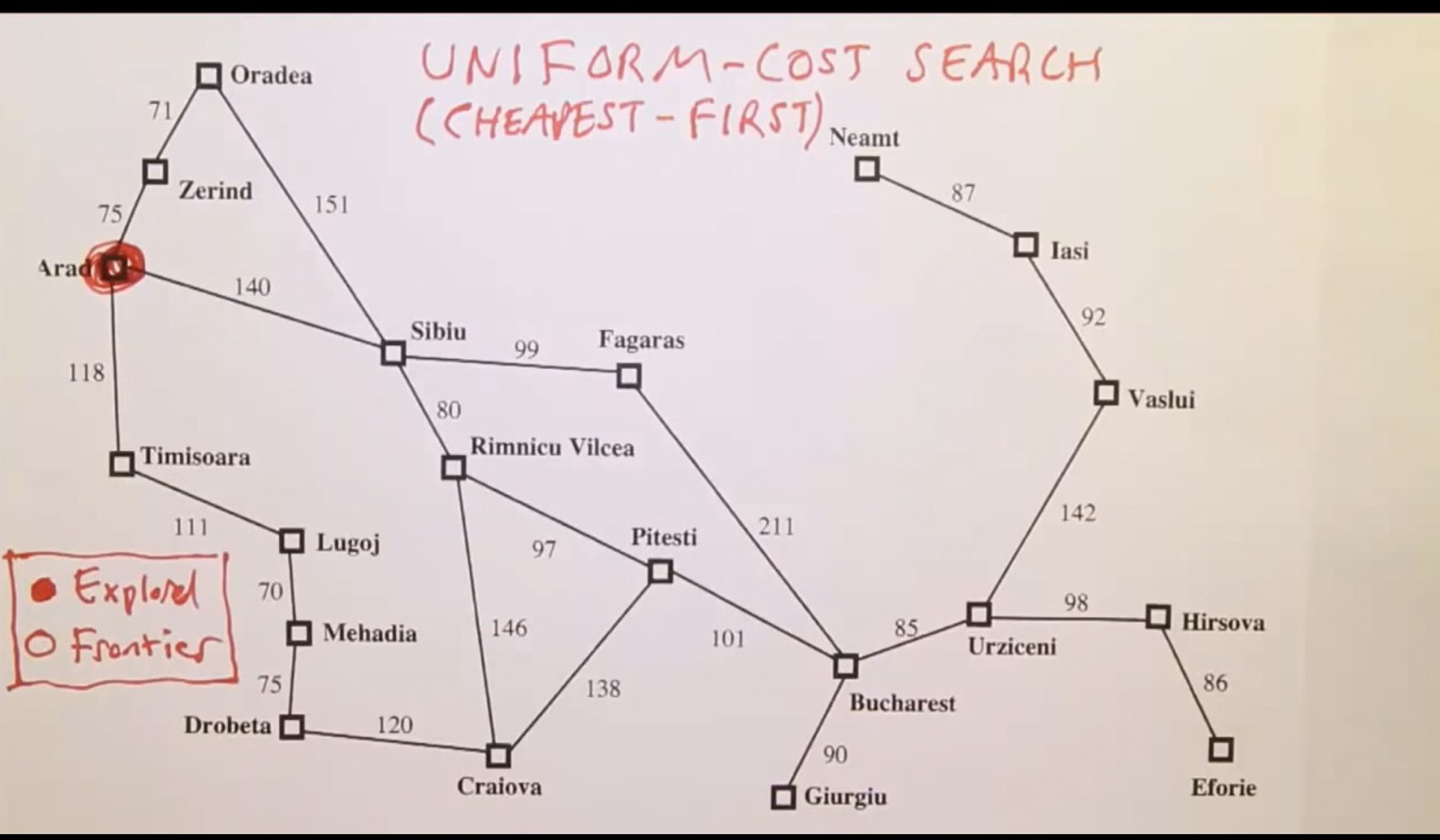
다음학기부터 조지아텍에서 Artificial Intelligence 라는 코스를 듣게 된다. 이 석사 과정 프로그램 중에서 굉장히 어려운 코스로 유명하다.. 개학하기 한달 전인 지금부터 조금이라도 들어놔야 살아 남을 수 있을 것 같다는 느낌이 ..

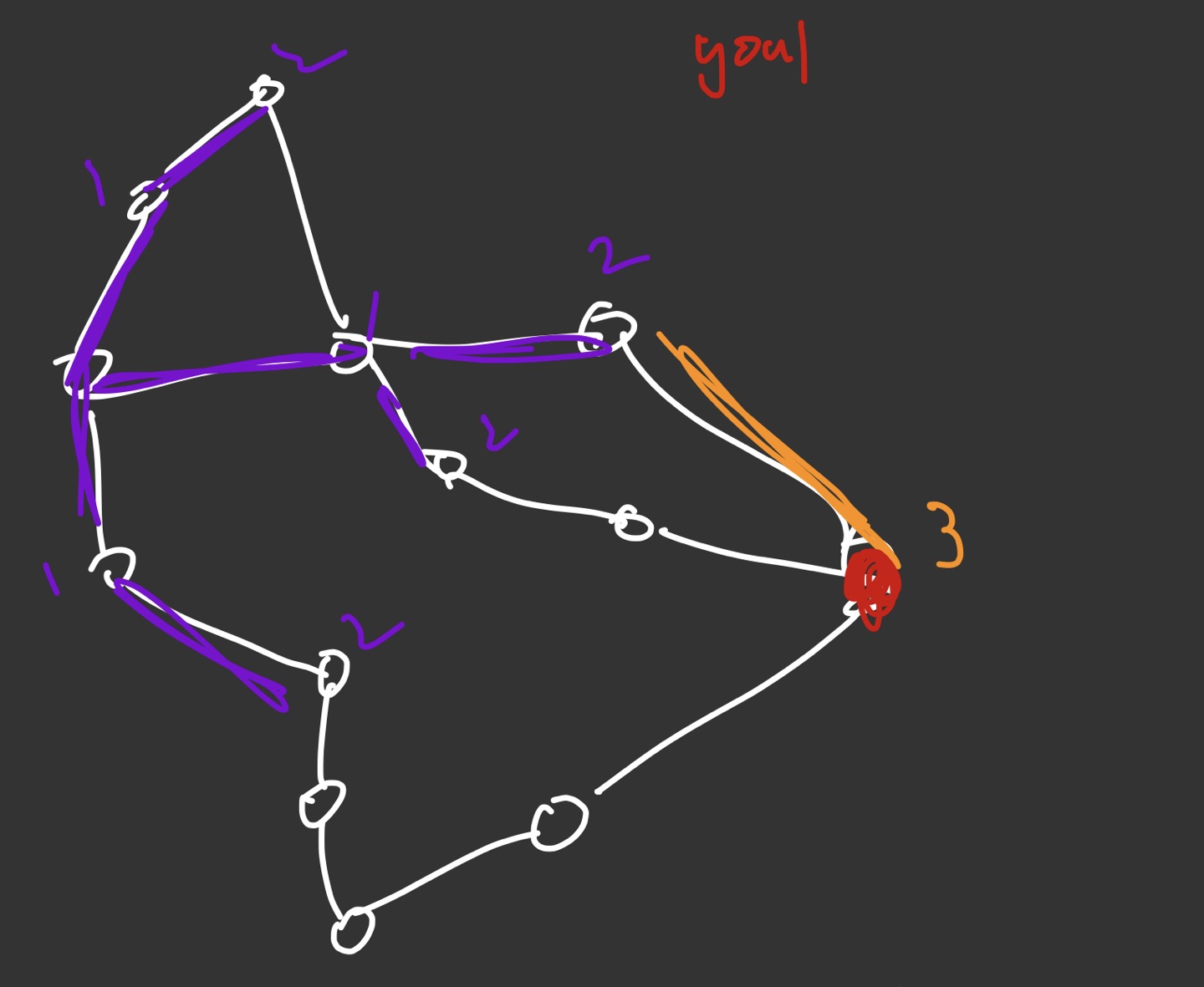
Breadth First Search (BFS) / Depth First Search (DFS) 서치 알고리즘 중 기초가 되는 BFS에 대해 얘기해보겠다.

저번 주차에서 다루었던 BFS와 DFS 같은 경우에는 사실 굉장이 직관적이고 1차원적인 탐색 알고리즘이라고 생각한다. 물론 이거 직접 코딩해보려고 하니까 고려해야할게 꽤 많았다 "사실 옆으로 펼치는 것" vs "아래로 내려가는 것" 만 생각하면 되는 알고리즘들이기 때문

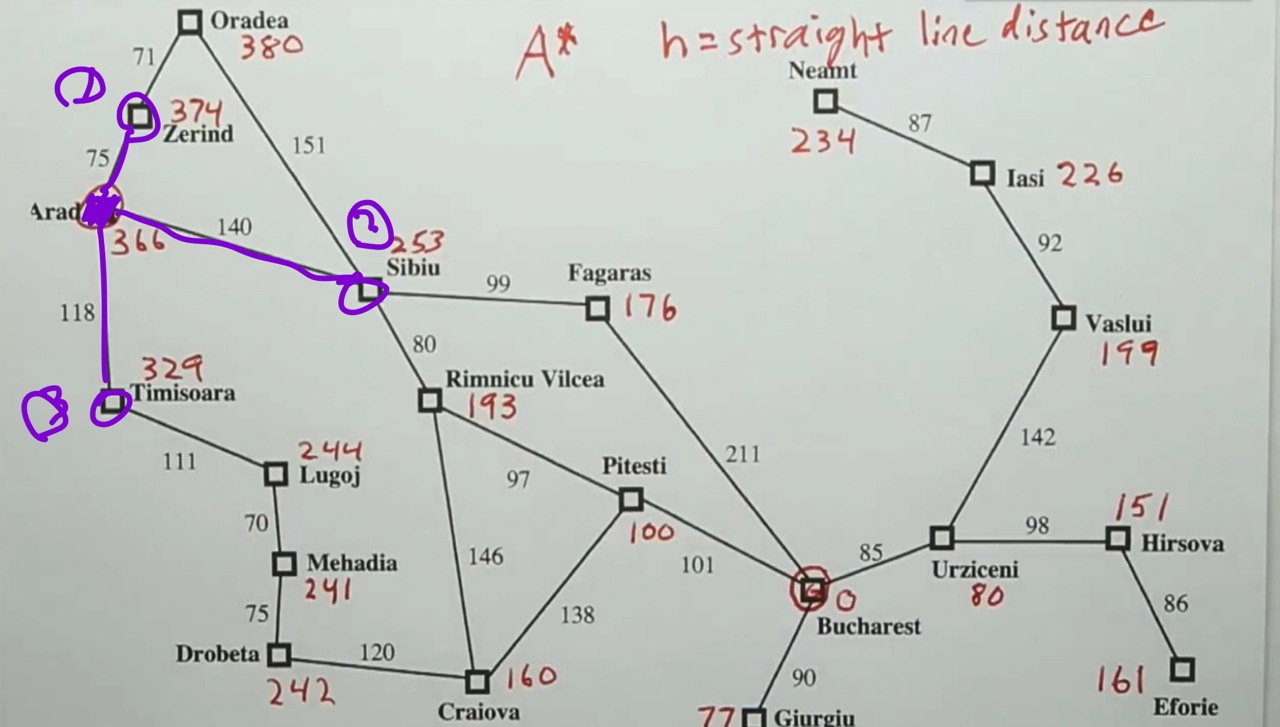
결국 UCS에서 제공해주는 최적화된 동선과, 경로 계산 효율성이라는 두 마리의 토끼를 모두 다 잡으려면 새로운 알고리즘을 사용해야한다는 결론으로 저번 주차 포스팅을 마쳤었다. 그렇다면 두 마리의 토끼는 어떻게 하면 잡을 수 있을까.

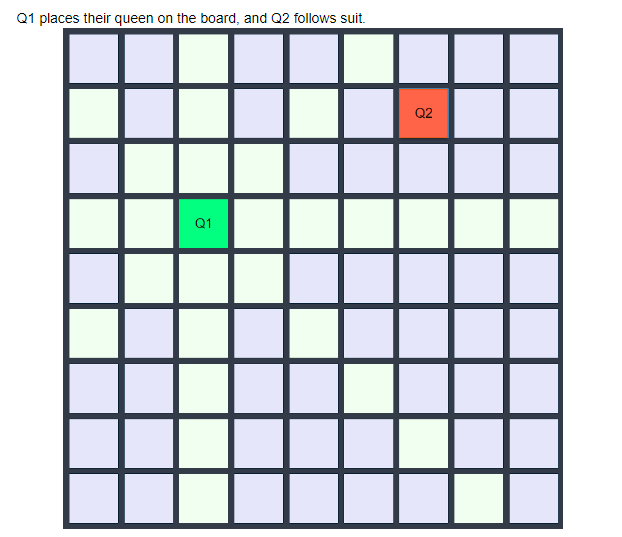
개인적으로 인공지능이 (AI) 란 단어 자체를 처음 접해본 것은 게임에서 였다. 어렸을때 유명했던 스타크래프트나 체스게임, 그리고 더 나아가 리그 오브 레전드에서도 AI, BOT 이란 이름으로 인공지능을 처음 접했던 것 같다.

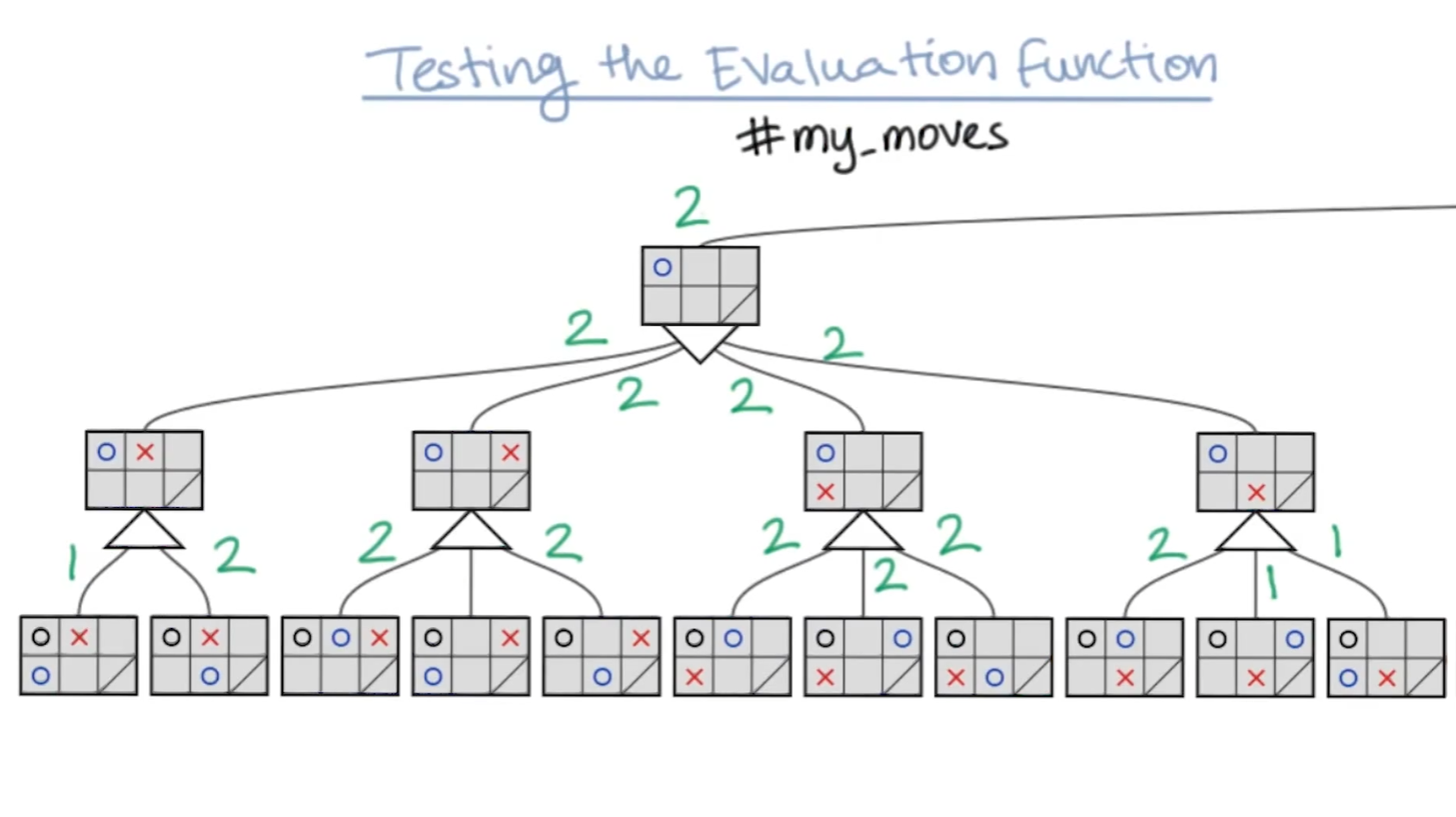
저번 주차에서 5x5 게임판의 모든 경우의 수를 계산하기 위해서는 25! 만큼의 계산량이 필요하다는 결과가 나왔었다. 하지만 이 결과값을 조금 더 현실적으로 볼 필요가 있다.

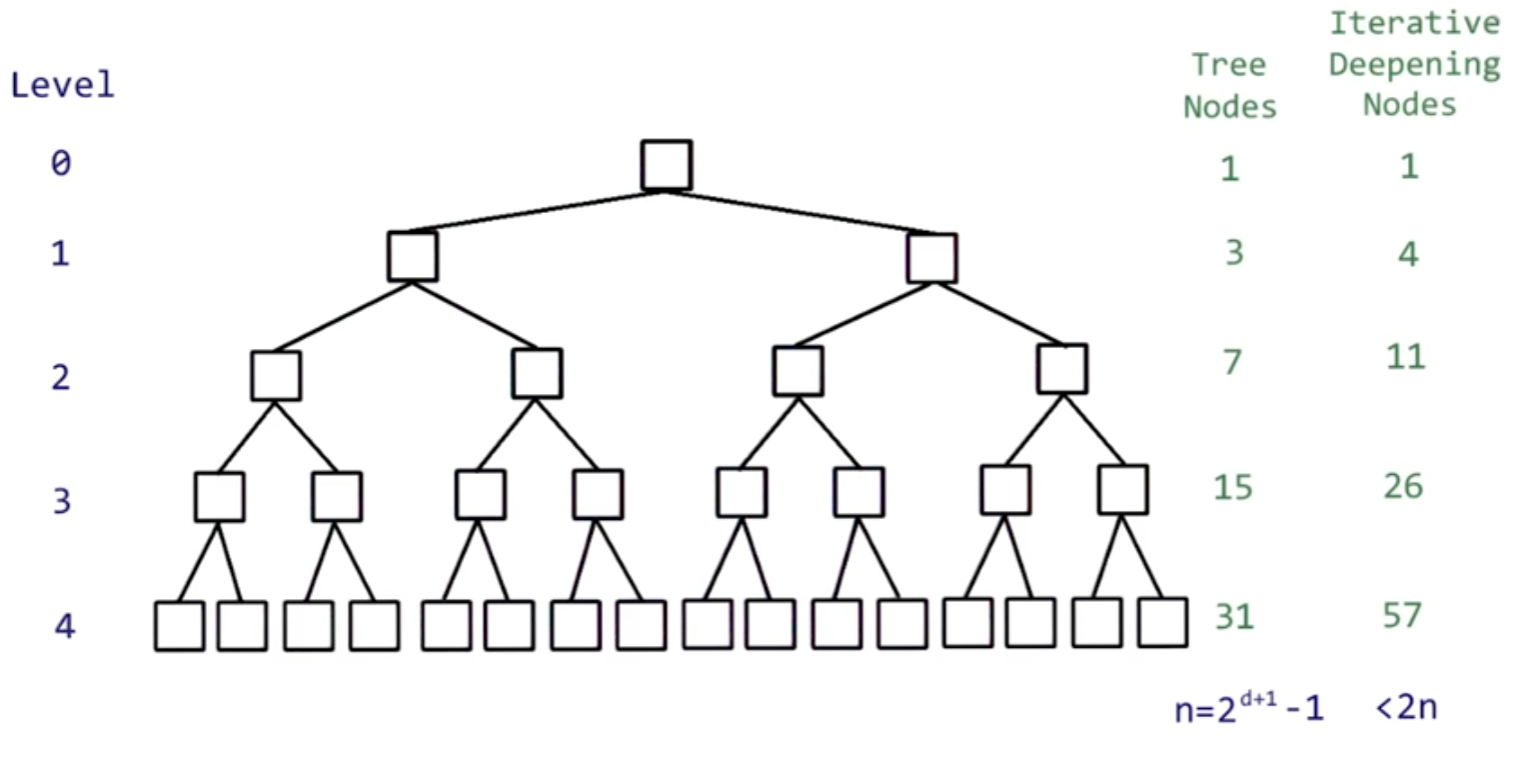
저번 주차에서 얘기했던 것과 같이, 찾는 깊이 제한을 둘 때마다 결과 값 (승패 및 해당 game state 에서 가능한 경우의 수 값) 이 달라지는 경우도 있었고, 끝 깊이에 가까워 질 수록 결과가 converge 하는 것을 볼 수 있었다.

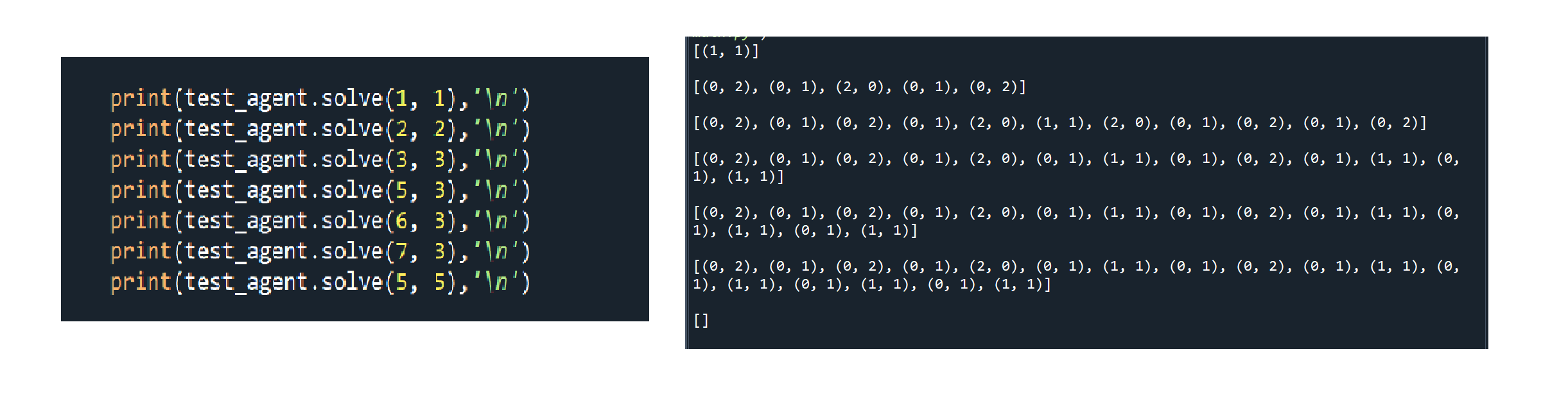
게임 인공지능을 떠나 잠시 서치 알고리즘 문제를 예제와 함께 해결해 보겠다. 예전 주차에서 서치 알고리즘을 다루었었는데 사실 이 알고리즘을 길찾기 뿐만 아니라, 조건만 충족된다면 충분히 다른 경우에서도 사용이 될 수 있다는 것을 되새기기 위해 이런 포스팅을 적어본다.

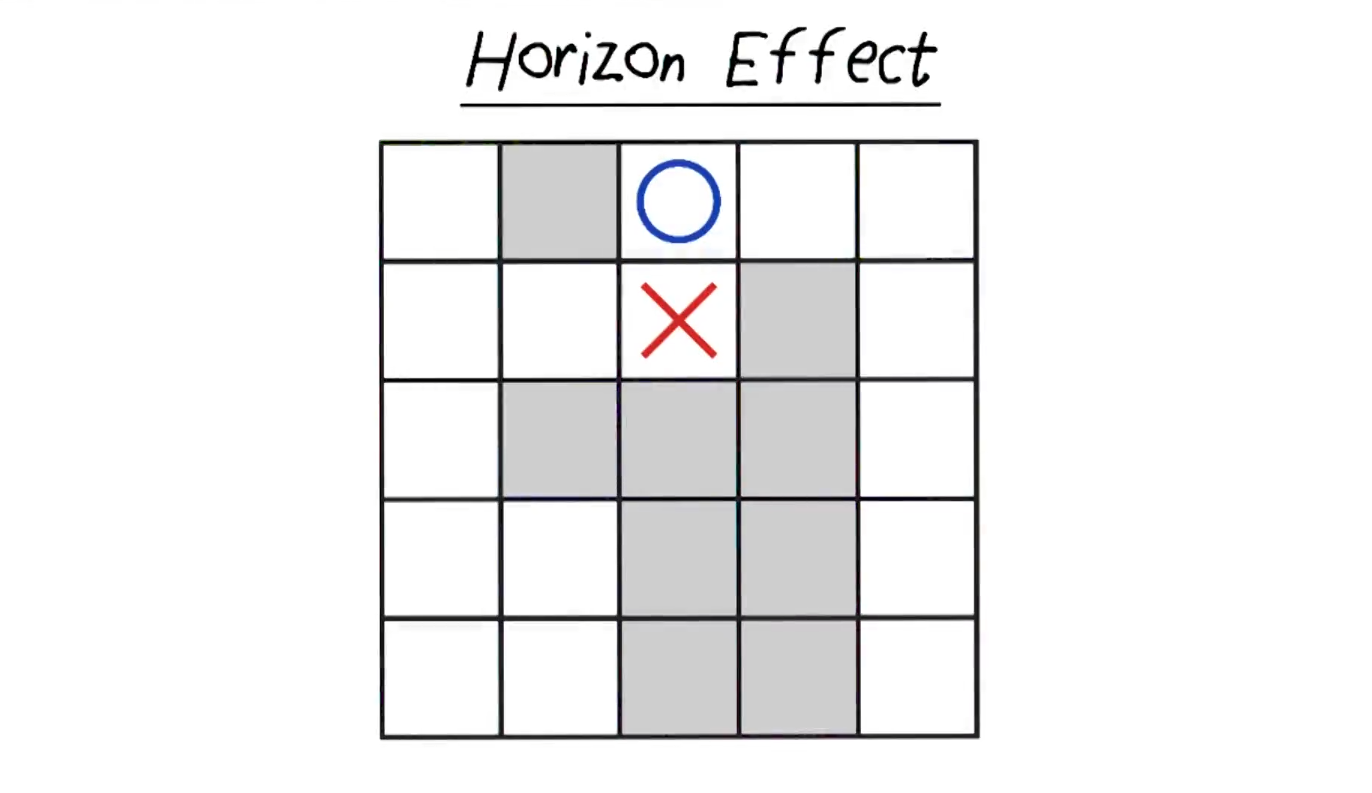
고립게임에서 고려해야 할 특수 사항이 존재한다. 밑의 그림을 예시로 보자.동그라미의 턴이라고 가정했을때, 어디로 움직이는 것이 승리의 결과값을 줄 수 있을까?