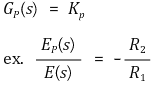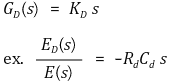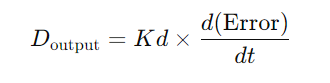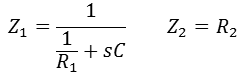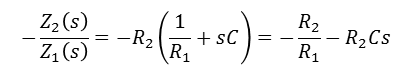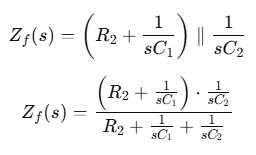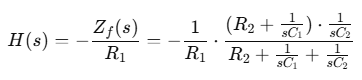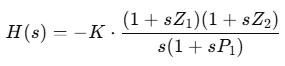제어
제어(Control)란, 시스템의 상태 X를 원하는 목표치 Xd로 도달시키는 과정
중점사항으로 보는 것은
① 성능 (Performance) : 성능은 시스템의 상태가 목표치에 부합한 정도
② 외란에 대한 안정성 (Stability) : 안정성은 시스템에 외란이 가해져도 발산하지 않는 것
- 설정값 (SV, Set point Variable), 목표값 : 제어의 목표가 되는 값.
제어량 : 제어 대상에 대해 제어해야 하는 양. 변화값
조작량 (MV, Manipulated Variable) : 제어량에 영향을 주는 것 중, 목표값에 도달하도록 이용하는 것.
측정값(PV, Process Variable) : 제어가 진행중일 때 현재 측정(출력)되고 있는 값
편차, 오차(e, error) : 측정값과 설정값의 차이값.
외란 : 사람의 힘이 미치지 못하지만 제어량을 변화시키는 원인
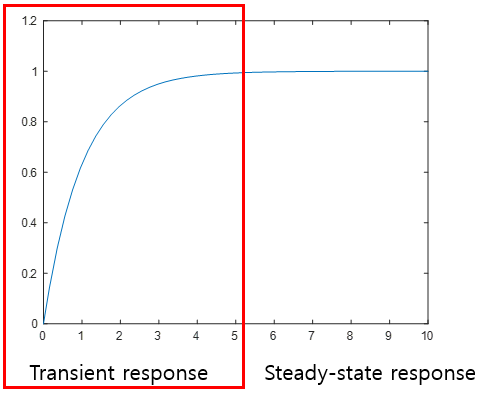
과도응답과 정상상태 응답
: 시간에 따른 시스템 상태 변화
용어
-
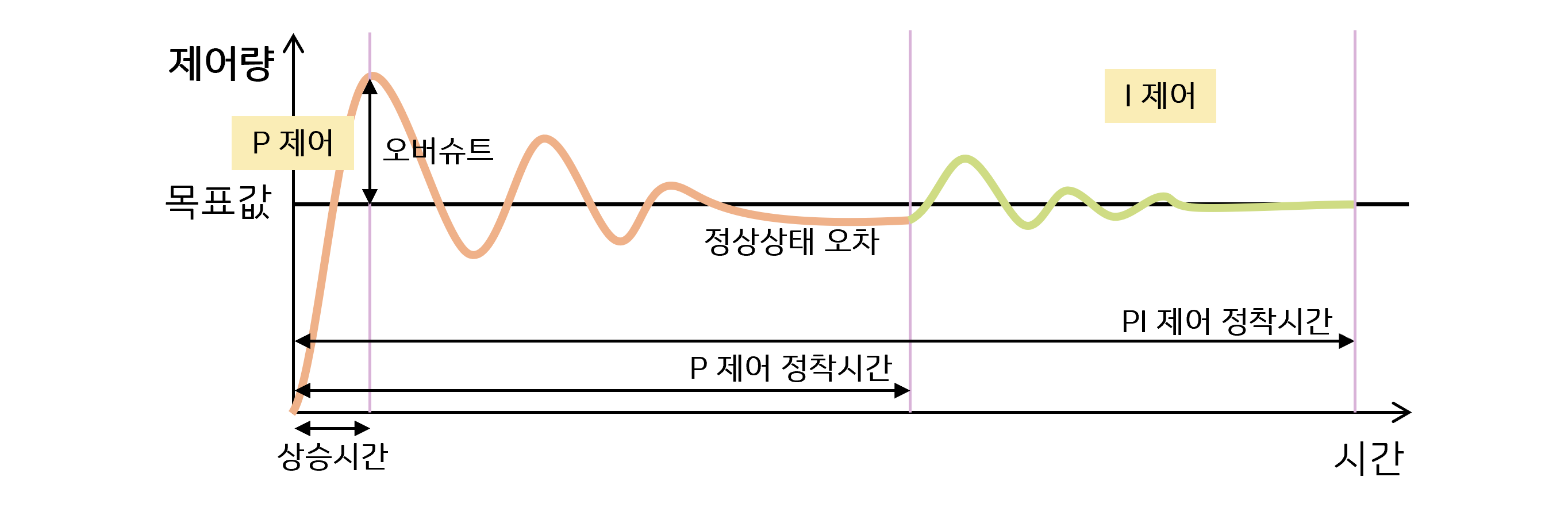
상승 시간 (Rising Time) : 10%에서 90%까지 상승하는 시간
정정 시간 (Settling Time) : 최종값의 ±5% (또는 ±2%)에 도달하는 시간
지연 시간 (Delay Time) : 최종값의 50%에 도달하는 시간
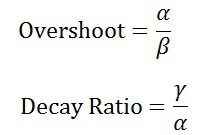
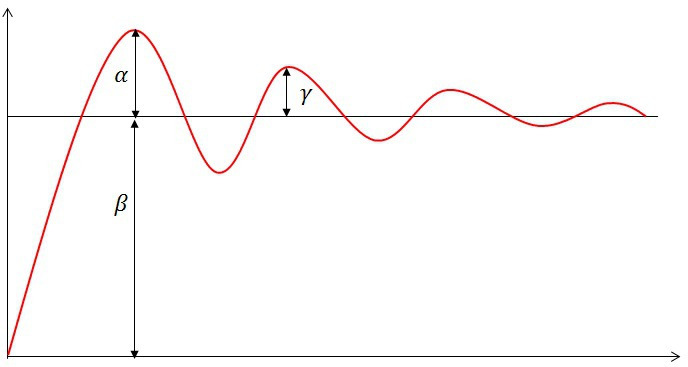
오버슈트 (%) : 최대 오버슈트 / 최종값 * 100 =
감쇠비 : 제 2 오버슈트 / 최대 오버슈트 -
과도응답 (transient response) :
출력이 정상상태가 되기 전의 시간에 나타나는 응답
시간에 따른 불안정한 초기 응답 -
정상 상태란 시간에 대해 변화가 없는 안정된 상태
정착시간이란 시작부터 정상상태가 될 때까지 걸리는 시간
정상 상태 오차 (steady-state error) 는 제어 시스템이 안정 상태에 도달했을 때, 목표 입력과 실제 출력 간의 지속적인 차이 -
오버슈트는 목표값보다 오차가 커지는 것
반대 개념은 언더슈트(Undershoot)
상승시간이란 0에서부터 처음 오버슈트가 될 때까지 걸리는 시간.
정리
| 요소 | 정의 및 기능 | 예시 |
|---|---|---|
| ① 목표값 (Setpoint, SV) | 시스템이 도달해야 할 기준값 (목표) | 5V 출력, 100°C 온도, 1500 rpm |
| ② 제어 대상 (Plant) | 실제로 제어되는 시스템, 출력이 발생하는 부분 | DC-DC 컨버터, 모터, 히터 |
| ③ 측정기 (Sensor / Feedback) | 출력 상태를 측정해 피드백으로 사용 | 전압 센서, 온도 센서, 포토 인터럽터 |
| ④ 오차 계산기 (Comparator / Error Amp) | SV와 현재 상태의 차이를 계산 | OP AMP, MCU의 산술 계산 |
| ⑤ 제어기 (Controller) | 오차를 입력으로 받아 적절한 제어량 생성 | PID 컨트롤러, 디지털 루프 필터 |
| ⑥ 제어 소자 (Actuator / Driver) | 제어 신호를 물리적 작동으로 바꿈 | MOSFET, 릴레이, 파워 트랜지스터 |
| ⑦ 출력 (Output) | 사용자나 외부 시스템이 실제로 관측하는 결과 | 전압, 전류, 속도, 위치 |
| ⑧ 피드백 루프 (Feedback Path) | 출력 정보를 다시 제어기로 되돌리는 경로 | 저항 분압기, 센서 회로 |
| ⑨ 외란 (Disturbance) | 제어 대상에 영향을 주는 비의도적 입력 | 부하 변화, 온도 변화, EMI |
| ⑩ 기준 생성기 (Reference Source) | 고정되거나 조정 가능한 목표 신호 생성기 | Bandgap IC, DAC, 트리머 |
| ⑪ 필터 / 보상기 (Compensator) | 주파수 특성 보정, 안정성 확보 | Type I/II/III Compensation 회로 |
| ⑫ 샘플러 / ADC | 아날로그 신호를 디지털로 변환 (디지털 제어용) | MCU의 ADC 입력 |
제어 시스템
개루프 제어 시스템 (Open-loop Control System)
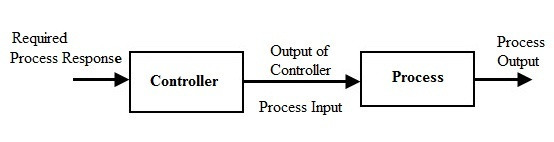
-
입출력 사이의 관계도 = 블록선도
제어 시스템은 입력(Input)과 출력(Output)으로 구성 -
개루프 제어시스템은 피드백이 없는 제어 시스템이다.
(피드백 : 실제 출력값을 점검하여 목표값과 일치하는지 비교하는 과정) -
개루프 제어시스템은 자동제어라 할 수 없다. (분류하자면 순서제어, 시퀀스제어)
결과(목표치) 에 대한 피드백이 없지만, 가격이 저렴하고 구조가 단순, 고장이 적음
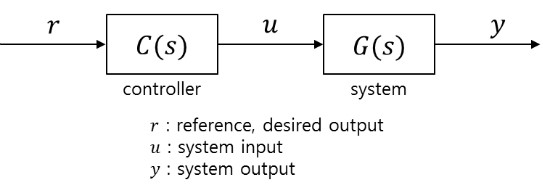
- Y(S) / R(S) = C(S) x G(S)
폐루프 제어 시스템 (Closed-loop Control System)
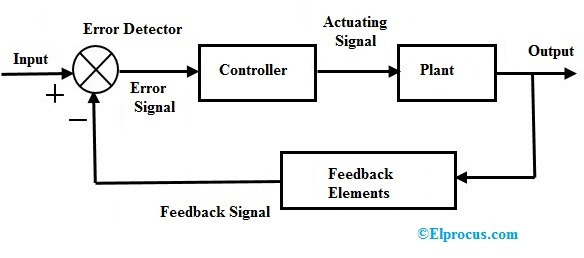
피드백 (에러, 출력조정 등 귀환요소) 이 있는 제어시스템은 폐루프 제어시스템
(자동제어 시스템으로 분류)
폐루프 제어시스템은 내부적인 파라미터 변화에 대한 감도를 줄일 수 있고 과도응답을 조절할 수 있지만, 제어시스템 구조가 복잡하고 비싸진다는 단점 있음
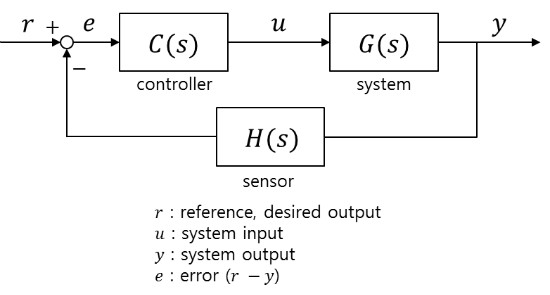
- Y(S) / R(S) = C(S) x G(S) / { 1 + C(S) x G(S) X H(S)}
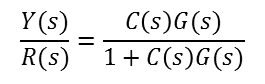
요약
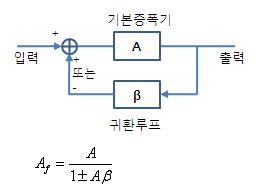
-
A : 개방 루프 이득 (Open-loop Gain)
귀환이 실제 없거나, 있어도 이를 고려치 않는 경우 => 개방 루프 또는 전방 경로 라고 칭함 -
Af : 폐쇄 루프 이득 (Closed-loop Gain)
귀환을 고려했을 때의 전체 시스템 이득 : Af = A / (1 ± Aβ) -
β : 귀환율 (Feedback Factor,Feedback Ratio)
출력 일부가 입력 쪽으로 얼마나 귀환되는지를 나타내는 비율 -
Aβ : 루프 이득 (Loop Gain) = 루프 전달함수 (Loop Transfer Function)
증폭기 이득(A)과 귀환율(β) 간의 곱 -
1 ± Aβ : 귀환량(Amount of Feedback) 또는 특성방정식
1 + Aβ : 부귀환 (Negative Feedback) =>부귀환 증폭기
1 - Aβ : 정귀환 (Positive Feedback) =>발진기
(특성방정식의 분모를 구성하며, 안정성과 관련됨)
피드백
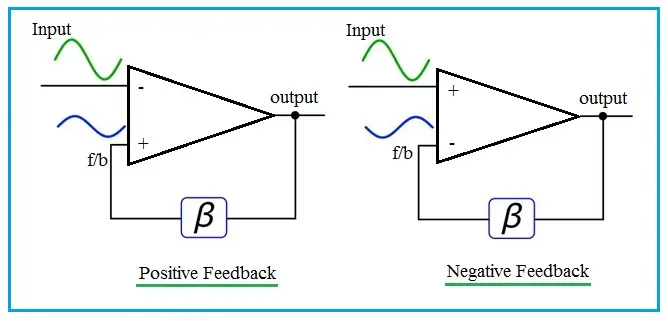
양의 피드백 (Positive Feedback)
- 출력 신호의 일부를 입력으로 다시 같은 방향으로 더하는 피드백 방식
출력이 증가하면 입력도 증가하게 되어, 결과적으로 출력 변화가 더욱 증폭
A : 오픈 루프 이득
𝛽 : 피드백 계수 (보통 0~1)
- Vout=A⋅(V𝑖𝑛 +βVout)
⇒ Vout= A⋅V𝑖𝑛 / (1−Aβ)
양의 피드백 효과
| 현상 | 설명 |
|---|---|
| 출력 불안정성 | 작동점이 고정되지 않고 출력이 한쪽으로 쏠림 |
| 이득 증가 | 입력 변화에 매우 민감한 시스템이 됨 |
| 발진 가능성 | 자체적으로 주기적인 신호를 생성 (발진기) |
| 히스테리시스 | 입력 변화에 따라 출력이 달라짐 (스위칭 지연 등) |
음의 피드백 (Negative Feedback)
- 출력 일부를 되돌려 입력과 반대 방향으로 작용하도록 만들어 오차를 줄이는 피드백 구조
출력이 증가하면 피드백이 입력 신호를 낮추는 방향으로 작동해 출력을 제어
출력 변화가 오차 증폭기 입력 전압차를 줄이는 방향으로 작용
A : 오픈 루프 이득
𝛽 : 피드백 계수 (보통 0~1)
- Verror = V𝑖𝑛 - βVout
Vout = A⋅Verror = A⋅(Vin − βVout)
⇒ Vout = A⋅V𝑖𝑛 / (1 + Aβ)
음의 피드백 효과
| 항목 | 내용 |
|---|---|
| 정의 | 출력 일부를 입력에 반대 방향으로 되돌리는 피드백 |
| 기능 | 오차 억제, 안정화, 선형화, 대역폭 증가 |
| 회로 예 | OP AMP 증폭기, LDO, 센서 회로 |
| 주의점 | 보상 회로 설계 필수, 위상 마진 고려 |
비교
| 항목 | 양의 피드백 | 음의 피드백 |
|---|---|---|
| 목적 | 증폭, 발진, 트리거 | 안정화, 정밀 제어 |
| 출력 변화 | 점점 더 커짐 | 오차 감소 |
| 적용 회로 | 발진기, 트리거, 비교기 | 증폭기, 전압 레귤레이터, 센서 회로 |
| 안정성 | 불안정함 | 안정적임 |
PID 제어
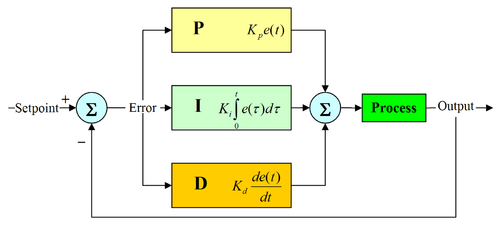
비례(P), 적분(I), 미분(D) 동작이 선형적으로 결합된 제어기
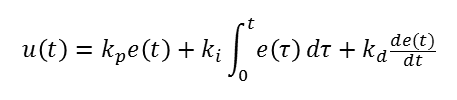
비례항 - 편차에 비례. 현재 상태에서 편차의 크기에 비례해 제어 작용
적분항 - 오차값의 적분(integral)에 비례, 정상 상태(steady-state) 오차를 없앤다.
미분항 - 오차값의 미분(derivative)에 비례. 출력값의 급격한 변화를 막아 오버슈트을 줄이며 안정성을 향상시킨다.
Kp, Ki, Kd 를 이득값(Gain, 게인)이라 함.
각각 비례 제어, 적분 제어, 편차 제어를 조절하는 계수
튜닝(Tuning)은 게인을 수학적/실험적/경험적으로 계산해 조정하는 것
PID 제어 블록
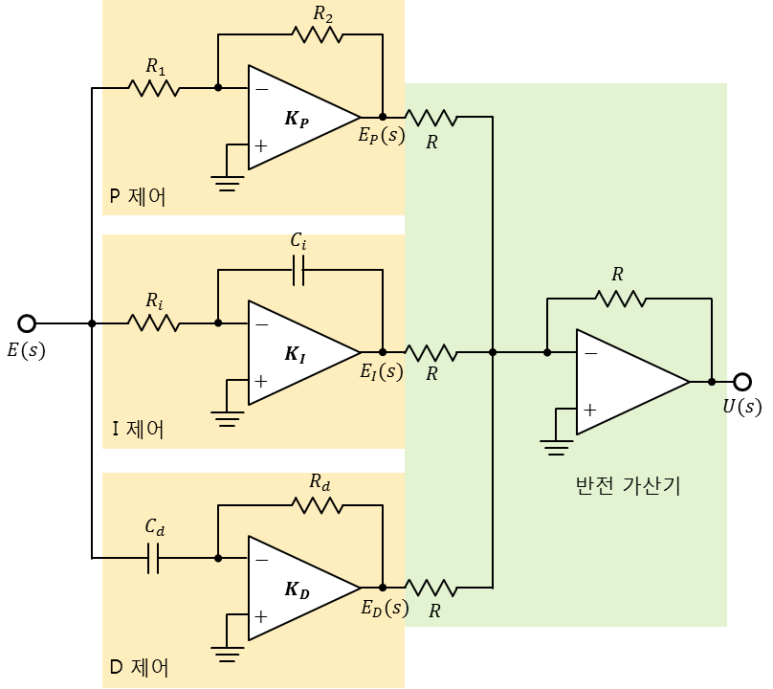
- P제어 블록 증폭비 : - R2 / R1
I제어 블록 증폭비 : - 1 / RCS
D제어 블록 증폭비 : - RCS
비례 제어기 (P)
(Proportional Controller) :
출력값과 목표값의 차이에 비례해 입력값 계산
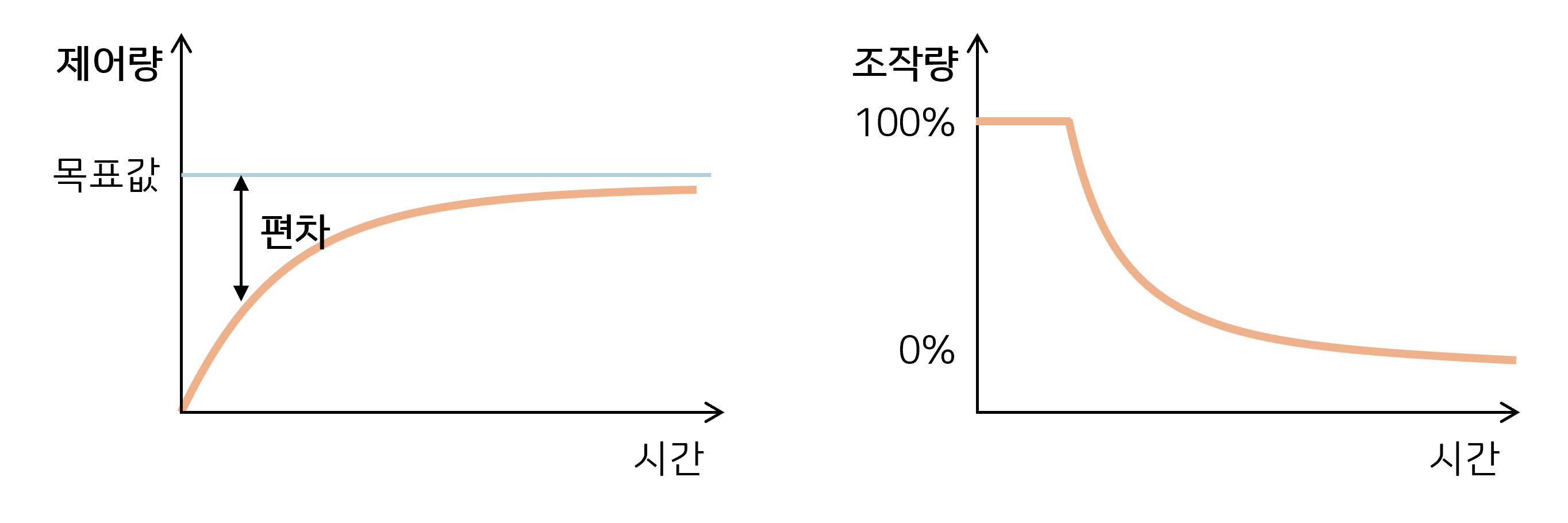
출력 = 𝐾𝑝 ⋅ 𝑒(𝑡)
P(비례) 제어는 제어량과 목표값의 차이(편차)에 비례하여 제어
-
Kp 값을 크게 하면 편차에 따른 조작량이 크므로, 상승시간이 줄어 빠르게 목표값에 도달, 오버슈트 값 증가
Kp 값을 작게 하면 상승시간 길어져 목표값에 느리게 도달, 오버슈트는 감소한다. -
정의: 현재 오차값에 비례하여 제어 신호를 출력
기능: 오차가 클수록 강하게 반응
한계: 오차가 0이 되면 출력도 0 → 잔류 오차 (steady-state error) 발생 -
오차 크기에 상수 비례 => 현재 중시 (즉응성)
제어기 출력이 제어기 입력에 비례적임
적분 제어기 (I)
(Integral Controller) :
오차의 누적값을 이용해 제어 입력합 계산
※ 구분구적법
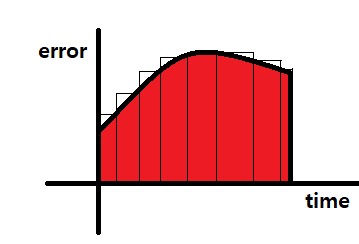
시간마다 발생한 오차를 더해줍니다
출처: https://wowon.tistory.com/169 [원원이의 블로그:티스토리]
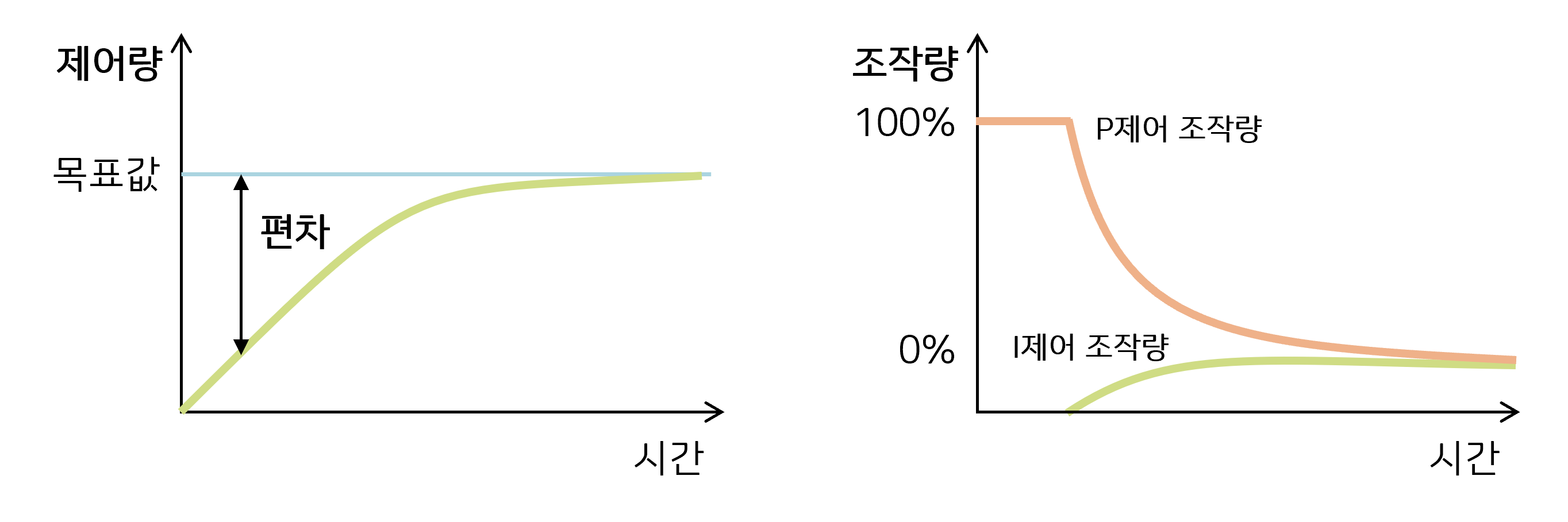
I 제어는 편차를 시간에 대해 누적(적분)하고, 누적값이 특정값이 되면 조작량을 증가시켜 편차를 없앰으로써 목표값에 더욱 정밀하게 접근하도록 한다.
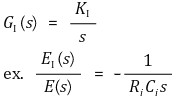
출력 = 𝐾𝑖 ⋅ ∫𝑒(𝑡)𝑑𝑡
- 정의: 과거 오차를 누적하여 제어에 반영
기능: 잔류 오차 제거 (영점 수렴)
한계: 누적 지연 발생 → 과도기 진동 또는 과충돌 위험
미분 제어 (D)
(Derivative Controller) :
출력값의 변화율에 기반하여 제어 입력값 계산
출력 = 𝐾𝑑 ⋅ {𝑑𝑒(𝑡)} / {𝑑𝑡}
- 정의: 오차의 변화율을 반영
기능: 변화 속도를 예측 → 과도기 억제, 빠른 반응 가능
한계: 노이즈에 민감, 과도하게 작용 시 시스템 불안정

미분 제어(D)는 목표량과 제어량의 편차를 비교해 반대되는 기울기로 조작하는 방식
-
𝐾𝑑 값이 클수록 안정화에 걸리는 시간이 줄어들어 정착시간이 감소된다.
정상상태에서는 D 제어보다 PI 제어의 영향이 커 정상상태 오차 변화는 거의 없다. -
D 제어는 편차와 반대 부호로 조작을 하기 때문에, 𝐾𝑑 값이 클수록 오버슈트는 감소하고 오차를 빨리 교정해, 상승시간과 정착 시간이 감소.
요약
종합 효과
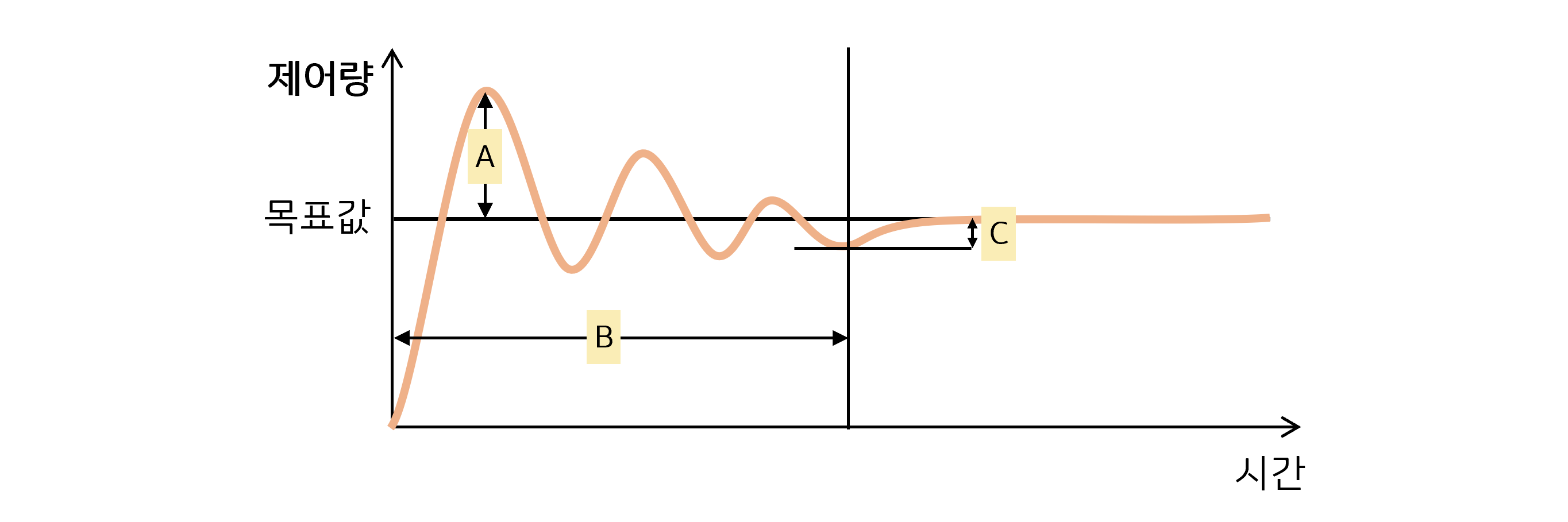
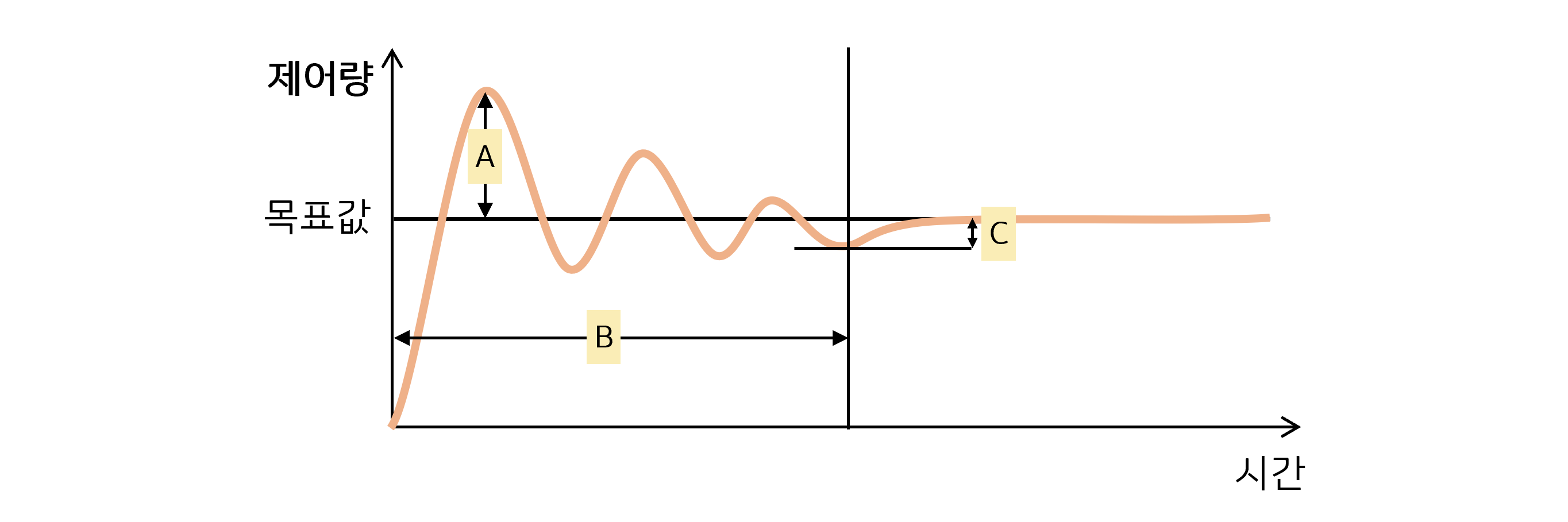
- P 제어: 목표값 도달 시간(B) 감소. 목표값과 멀수록 많이, 가까울수록 적게 조작.
I 제어: 정상 상태 오차(C) 감소. 목표값에 맞게하기 위해 미세하게 조정하여 편차 제거
D 제어: 오버슈트(A) 억제. 제어값 변화 억제.
| 요소 | 기능 | 효과 | 주의점 |
|---|---|---|---|
| P | 현재 오차 | 빠른 반응 | 잔류 오차 가능 |
| I | 오차 누적 | 오차 제거 | 느림, 진동 유발 |
| D | 오차 변화 | 예측 제어 | 노이즈 민감 |
요약
| 항목 | 내용 |
|---|---|
| 목적 | 오차를 최소화하고 빠르게 목표값에 수렴 |
| 구성 | 비례(P), 적분(I), 미분(D) 세 요소 |
| 효과 | 정확성(P+I), 안정성(D), 빠른 응답(P+D) |
| 튜닝 | Kp, Ki, Kd 값을 실험적/자동화 방법으로 조정 |
PD 제어 & PI 제어
PD 제어
- P 게인은 R2/R1, D 게인은 R2C를 통해서 설정
빠른 응답, 오버슈트 억제
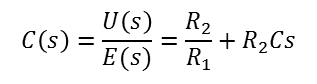
PI 제어
-

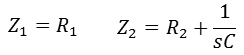
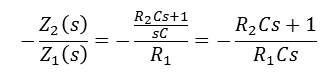
-
P 게인은 R2/R1, I 게인은 1/R1C를 통해서 설정
정확한 도달, 오차 제거
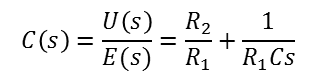
| 항목 | PI 제어기 | PD 제어기 |
|---|---|---|
| 비례(P) | 오차에 비례한 반응 | 동일 |
| 적분(I) | 오차 누적 → 오차 제거 | 없음 |
| 미분(D) | 없음 | 오차 변화 감지 → 빠른 대응 |
| 목표 | 정확한 값 도달 (오차 제거) | 빠른 응답, 예측 반응 |
| 정상 상태 오차 | 없음 (0으로 수렴) | 존재할 수 있음 |
| 잡음에 대한 민감도 | 낮음 | 높음 (D 성분은 노이즈에 매우 민감) |
지글러-니콜라스 방법
(Ziegler-Nichols Method)
-
시스템을 P 제어기만 사용 (I=0, D=0) 상태로 설정
-
비례 이득 Kp를 서서히 증가
-
시스템이 지속적인 진동(Sustained Oscillation) 을 보일 때 이득을 기록 → 임계 이득 Ku
-
해당 진동의 주기(Tu)를 측정 → 임계 주기
-
Ku와 Tu를 기준으로 PID 상수를 계산
튜닝 공식 (Ziegler–Nichols Table)
| 제어기 타입 | Kp | Ti (적분 시간) | Td (미분 시간) |
|---|---|---|---|
| P | 0.5 Ku | – | – |
| PI | 0.45 Ku | Tu/1.2 | – |
| PID | 0.6 Ku | Tu/2 | Tu/8 |
오차 증폭기
오차 증폭기(Error Amplifier)는 피드백 제어 시스템의 중심에 있는 고이득 연산 증폭기
목표 출력(기준 전압)과 실제 출력(피드백 전압) 사이의 오차(error) 를 감지하고 증폭하여 출력을 조절하는 신호를 생성
기준 값(Reference)과 피드백(feedback) 값의 차이를 증폭하여 출력이 기준에 수렴하도록 제어 신호를 생성
-
VREF : 목표 기준 전압 (예: 1.25V)
VFB : 출력 전압 일부를 분압하여 얻은 피드백 전압
오차 (E) = VREF – VFB
출력 신호는 이 오차를 기반으로 만들어진 보정 신호 (compensated control) -
비교 및 증폭 : Verr = Av (Vref – Vin)
| 상태 | 오차 증폭기 반응 | 제어기 동작 |
|---|---|---|
| 출력 전압 ↓ | VFB < VREF → 출력 ↑ | PWM 듀티 ↑, 전압 ↑ |
| 출력 전압 ↑ | VFB > VREF → 출력 ↓ | PWM 듀티 ↓, 전압 ↓ |
예시: SMPS 피드백 루프에서의 오차증폭기 작동
-
목표 설정: 기준 전압 Vref = 2.5V
-
피드백: 출력 전압이 5V라면 저항 분압기로 2.5V 피드백 생성
-
비교: 오차증폭기에서 Vref - Vfb = 0 → 오차 없음 → 출력 유지
-
출력 전압이 올라가면:
Vfb > Vref → 오차 음 → Verror 감소 → PWM 듀티 감소 → Vout 낮아짐 -
출력 전압이 내려가면:
Vfb < Vref → 오차 양 → Verror 증가 → PWM 듀티 증가 → Vout 높아짐
이처럼 Vout이 Vref에 수렴되도록 루프가 지속적으로 조정됨
OP AMP (연산 증폭기)는 폐루프(Closed-Loop) 구성 하에서
입력 단자(+와 −)의 전압을 같게 하려는 성질 존재
(두 입력의 전압 차를 0으로 만들려는 성질)
-
가상 단락 (virtual short)
연산 증폭기는 내부적으로 전압 이득이 매우 큰 증폭기 (10^5 ~ 10^6)
폐루프 피드백이 존재할 경우, OP AMP는 출력을 조절해서 +와 − 입력의 전압을 거의 같게 만듬
Vout = Av (V+ – V–) -
전류의 흐름: 가상 접지 (Virtual Ground)
이상적인 OP AMP는 입력 임피던스가 무한대이므로, 입력 단자에는 전류가 흐르지 않음
이와 결합된 개념이 가상 접지 (virtual ground)
비반전 입력(+)이 0V(접지)에 연결된 경우, 피드백을 통해 반전 입력(−)도 0V
접지된 것처럼 전압이 0”인 것이지, 실제로 접지된 건 아님
| 이유 | 설명 |
|---|---|
| OP AMP의 높은 이득 | 작은 입력 전압 차이도 큰 출력 변화 유도 |
| 피드백 회로 존재 | 출력이 조절되어 입력 전압 차이를 줄이게 만듦 |
| 회로 안정 조건 | 출력이 안정되려면 이어야 함 |
| 가상 단락 원리 | 결과적으로 두 입력 전압이 같아지는 현상 발생 |
기본형
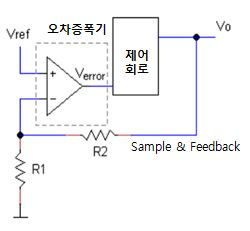
기준 전압과 피드백 신호를 OP AMP의 두 입력에 연결
Vout = Vref (1+R1/R2)
보상형 (PI 제어 회로)
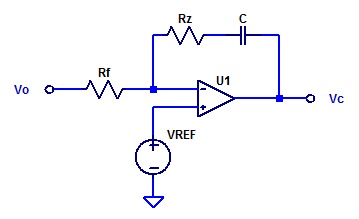
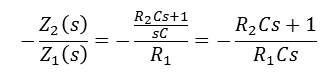
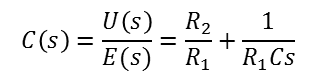
비례(Proportional) + 적분(Integral) 보상 포함
출력 안정성과 정상 상태 오차 제거에 강점
보상기
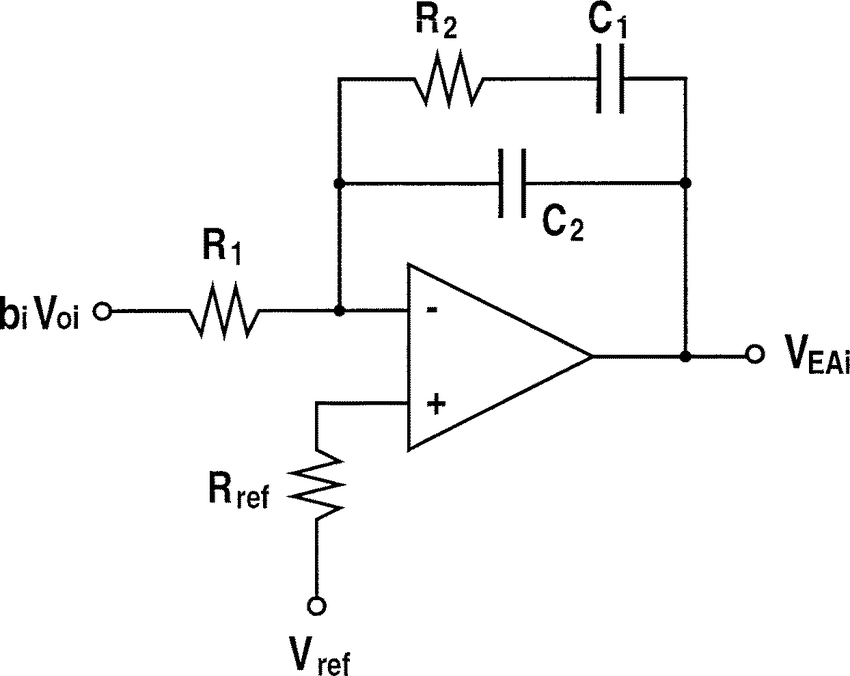
영점 2개, 극점 1개, 원점 극점 1개 포함
Ref
https://upload.wikimedia.org/wikipedia/commons/thumb/4/40/Pid-feedback-nct-int-correct.png/500px-Pid-feedback-nct-int-correct.png
http://www.ktword.co.kr/test/view/view.php?no=4670
https://blog.naver.com/lagrange0115/222050194980
https://blog.naver.com/lagrange0115
https://velog.io/@717lumos/Control-PID-%EC%A0%9C%EC%96%B4#3-2%EC%9D%B4%EB%93%9Dgain
https://pus0319.github.io/embedded_control/PIDCONTROL/
http://ktword.co.kr/test/view/view.php?no=5334
https://2n3904blog.com/low-noise-high-psrr-ldo-error-amplifier/
출처: https://gammabeta.tistory.com/1295 [BOOK:티스토리]