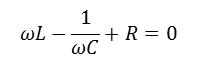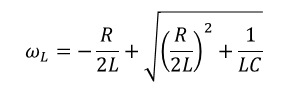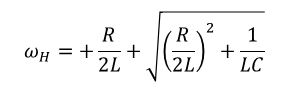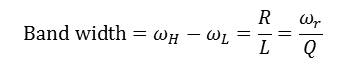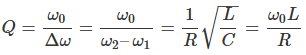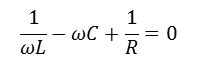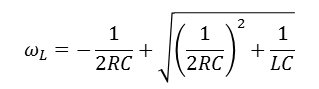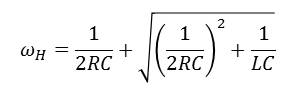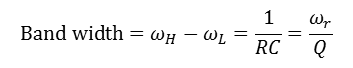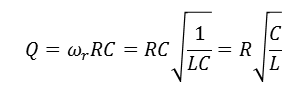RLC 공진회로

myblack·2024년 9월 6일

RLC 공진 회로이론

회로이론

목록 보기

6/8

공진

공진이란 특정 진동수 (고유 주파수 영역)에서 큰 진폭으로 진동하는 현상

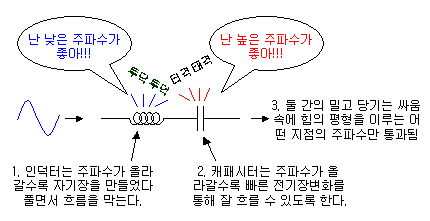
커패시터는 전압 변화에 따라 에너지를 전기장에 저장하고,
인덕터는 전류 변화에 따라 에너지를 자기장에 저장
이 둘이 서로 에너지를 주고받으면서 진동하며, 특정 주파수에서 위상이 일치하여 공진 발생

RLC 회로에서의 공진

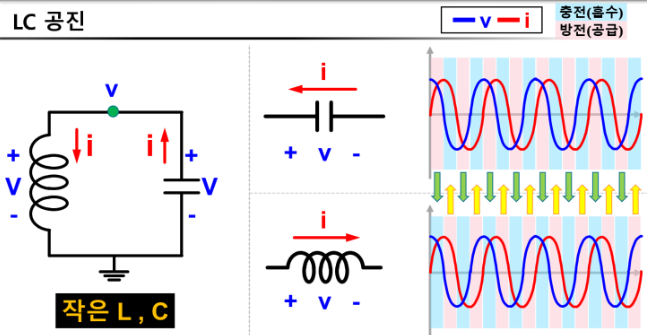
LC회로에서 1V 일때
인덕터에 DC전압 걸리지 않아 커패시터에 1V 걸려 충전됨.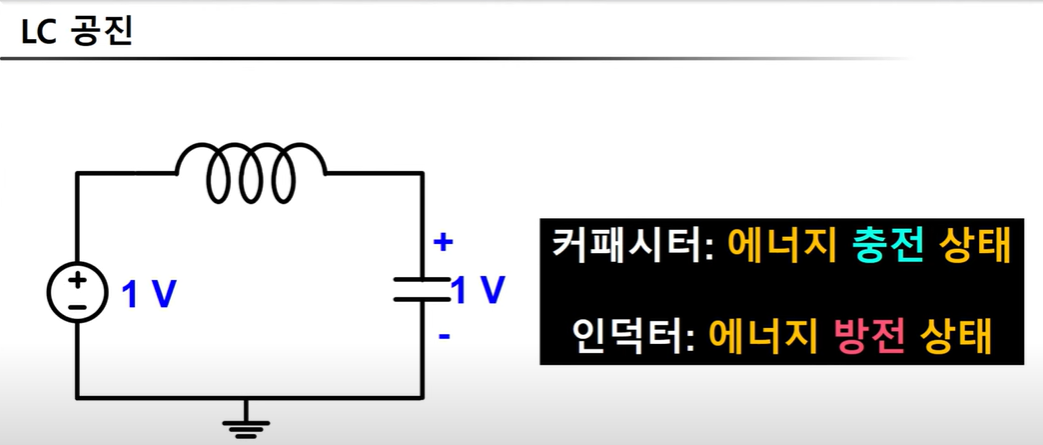

LC회로에서 전원 0V 일때
Cap이 1V로 충전되어 있으므로 인덕터쪽으로 전류가 흐르기 시작함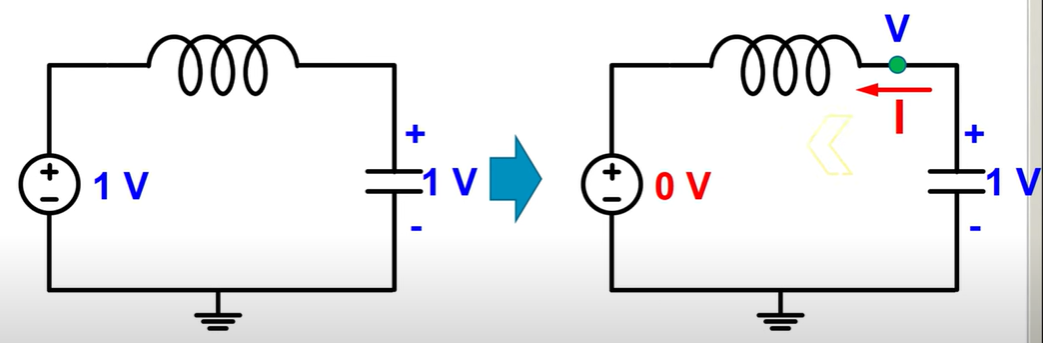

0V 전압원은 양단 전원이 0V이므로 단락으로 대체

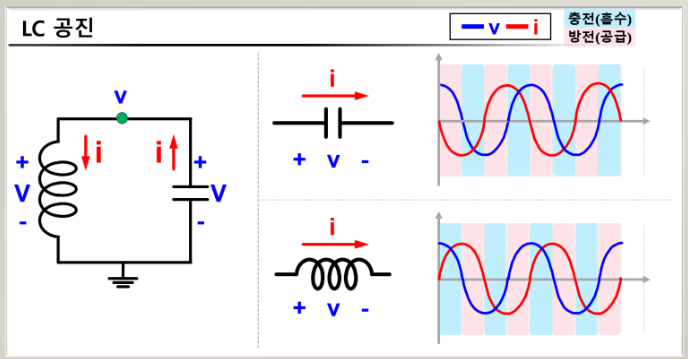
커패시터의 경우 전압의 위상보다 전류의 위상이 90도 빠름
전압과 전류의 부호가 같을 때, 커패시터 충전
전압과 전류의 부호가 다를 때, 커패시터 방전
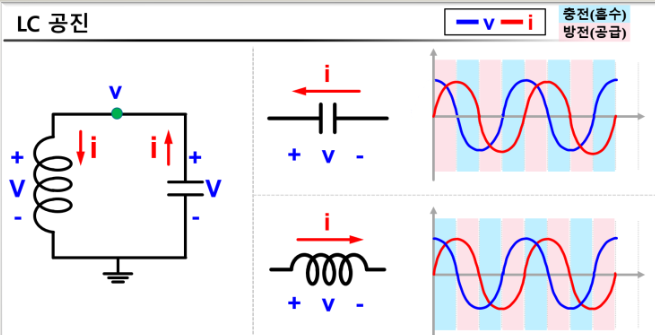
인덕터의 경우 전압의 위상보다 전류의 위상이 90도 느림
전압과 전류의 부호가 같을 때, 커패시터 충전
전압과 전류의 부호가 다를 때, 커패시터 방전
인덕터와 커패시터 전압전류 파형이 반대
커패시터 방전 : 인덕터 충전
커패시터 충전 : 인덕터 방전
에너지를 주고 받는 공진 현상 발생
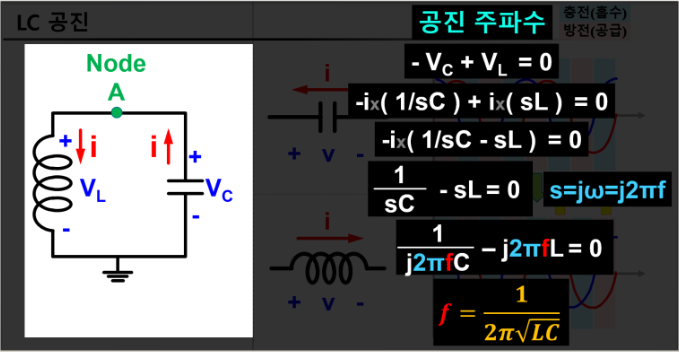
1 / 에너지 주고받는 시간 = 공진 주파수

LC값 변화

공진주파수 Q = CV

인덕터나 커패시터 값 작아지면 에너지(전하량) 감소
에너지 주고 받는 속도 빨라짐 -> 공진주파수 증가
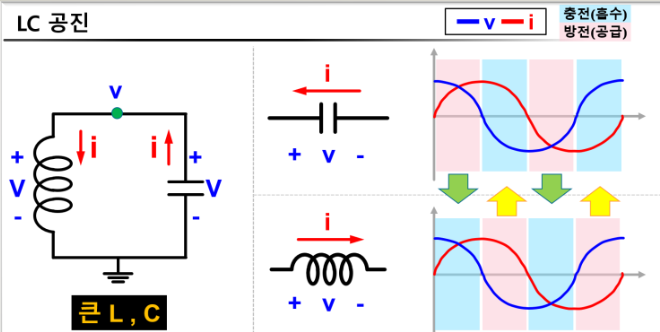
인덕터나 커패시터 값 커지면 에너지(전하량) 증가
에너지 주고 받는 속도 느려짐 -> 공진주파수 감소

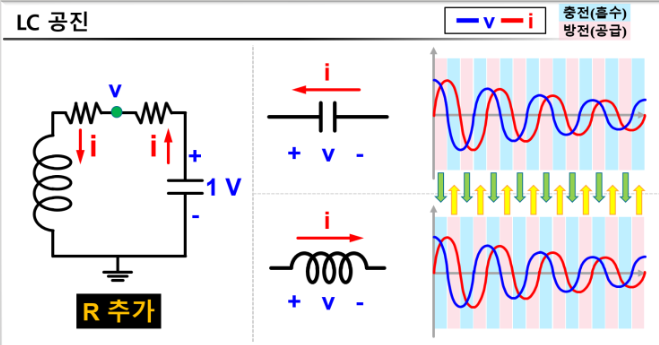
저항 추가 : 에너지 소모시켜 시간 지나면 전압 전류가 0이 되도록 함

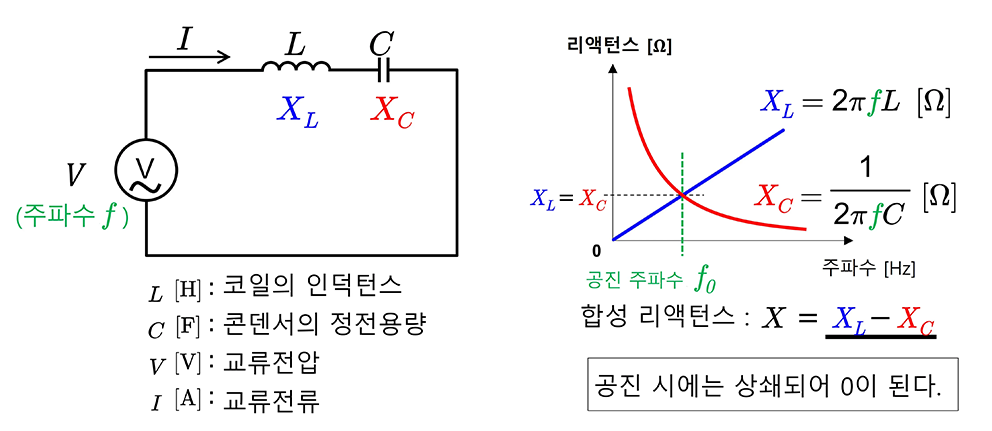
RLC 직렬회로

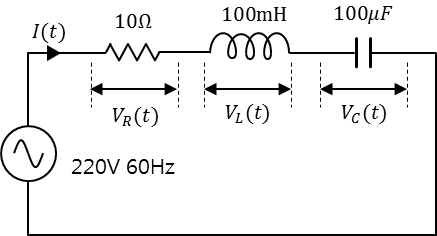
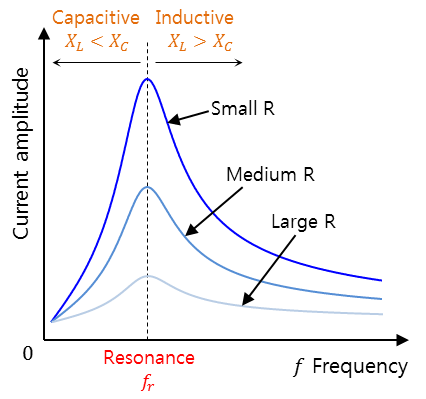
임피던스

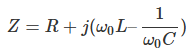
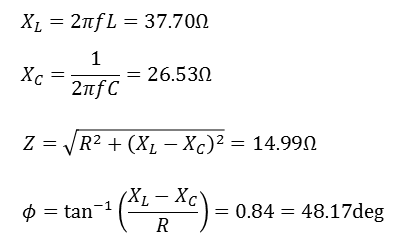
전류값

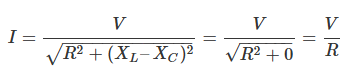
RLC 직렬 회로에서 콘덴서와 인덕터의 리액턴스가 동일해질 때 임피던스는 저항 성분만 남음
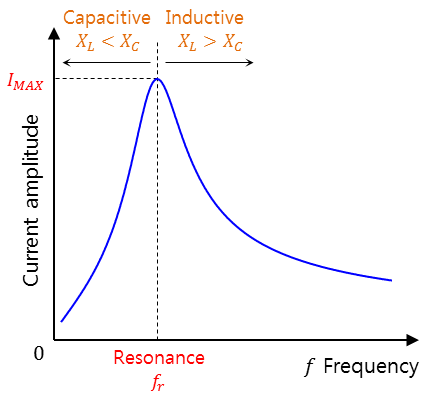
임피던스는 최소가 되고 회로 내에서의 전류는 최대
(Z = 최소, I = V/Z 최대 )

공진주파수

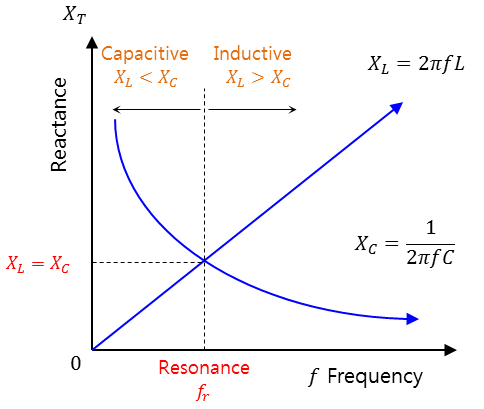
XL=XC 를 만족시키는 지점이 리액턴스 합의 최소점, 공진 주파수

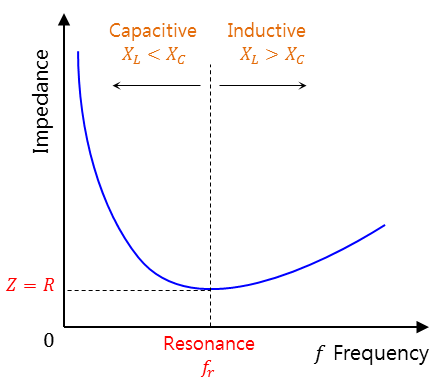
XL < XC 용량성
XL > XC 유도성

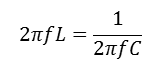
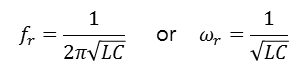
주파수 인자 변화

주파수에 따른 임피던스 변화

주파수에 따른 전류 변화

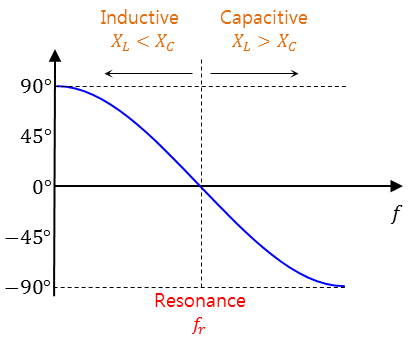
주파수에 따른 전압 전류 위상변화

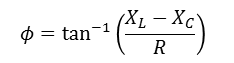
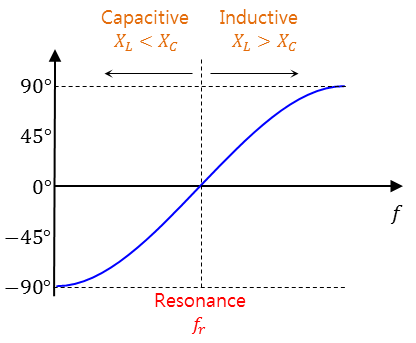
저항값에 따른 진폭 변화

RLC 병렬회로

임피던스

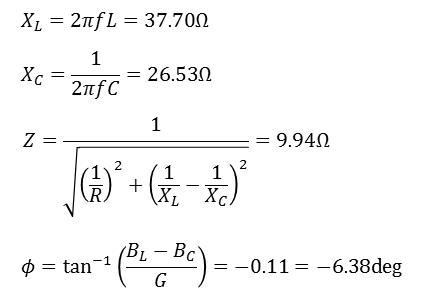
어드미턴스

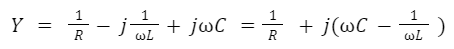
서샙턴스(B) = 0이 되면 임피던스 Y =1/R 인 회로

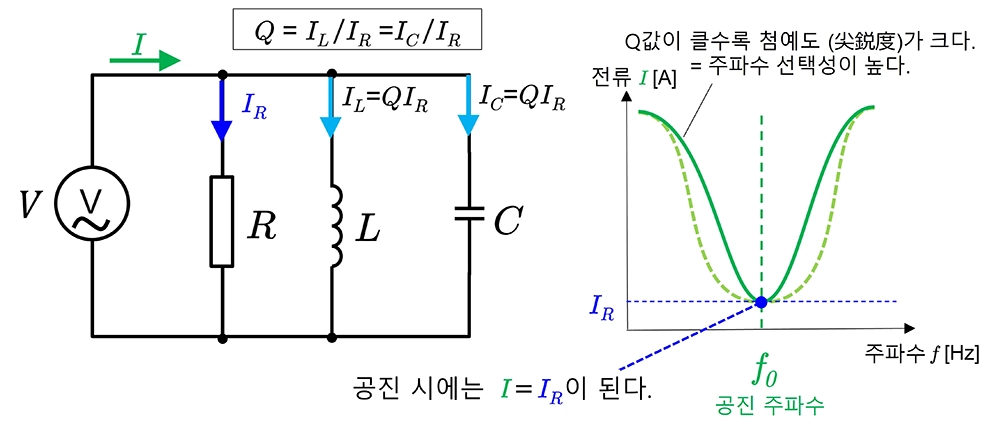
※ RLC 병렬 회로에서 콘덴서와 인덕터의 리액턴스가 임피던스는 최대, 전류는 최소
(직렬공진시 Y = 최소, I = Y*Z 최소 )

주파수 인자 변화

공진점

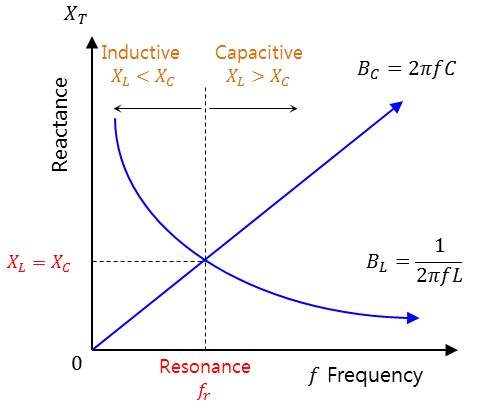
주파수-임피던스 어드미턴스 변화

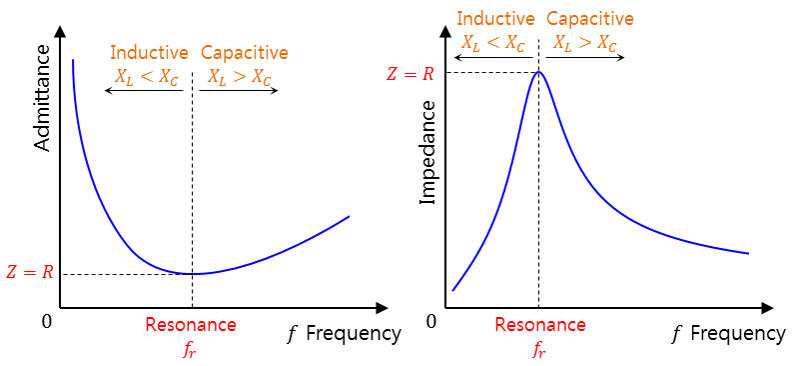
주파수에 따른 RLC 병렬 회로의 전압-전류 위상

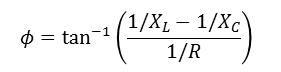
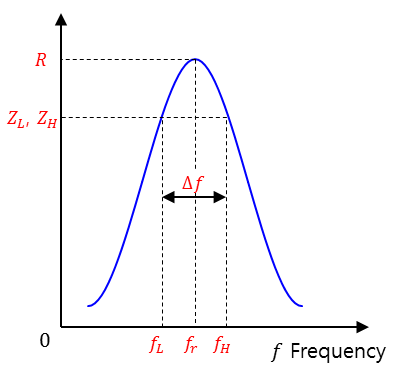
대역폭

Quality Factor

-Q값 (Quality Factor)은 신호의 첨예도나 선택성을 정량화하는 지표
Q값이 높으면 신호 특성의 첨예도가 높고, Q값이 낮으면 그 특성이 완만
Q값이 높은 회로는 좁은 대역의 신호를 한층 더 정밀하게 검출가능함

Q값과 반비례 관계인 밴드폭은 공진 회로가 효율적으로 통과시킬 수 있는 주파수 범위

BW = fo / Q

직렬 RLC : R/L
병렬 RLC : 1/RC

RLC 직렬 Q-factor & BW

대역폭 (Bandwidth)
진폭(magnitude)의 최대 값을 루트 2로 나눈 크기에 해당하는 주파수 폭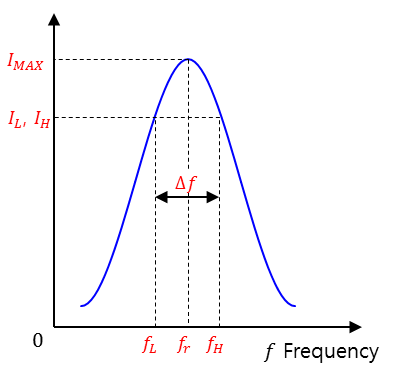

IL = IMAX / √2
공진때 리액턴스 0 이므로 -> Z = √2R
XL - XC = -R

RLC 병렬 Q-factor & BW

대역폭 (Bandwidth)
진폭(magnitude)의 최대 값을 루트 2로 나눈 크기에 해당하는 주파수 폭

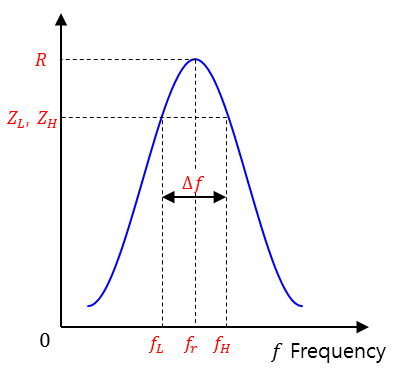
ZL = ZMAX / √2 = R / √2

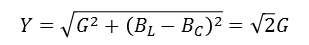
BL - BC = -G

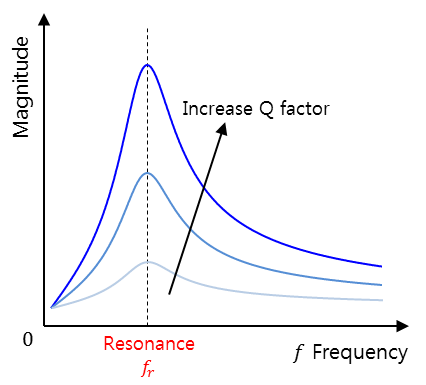
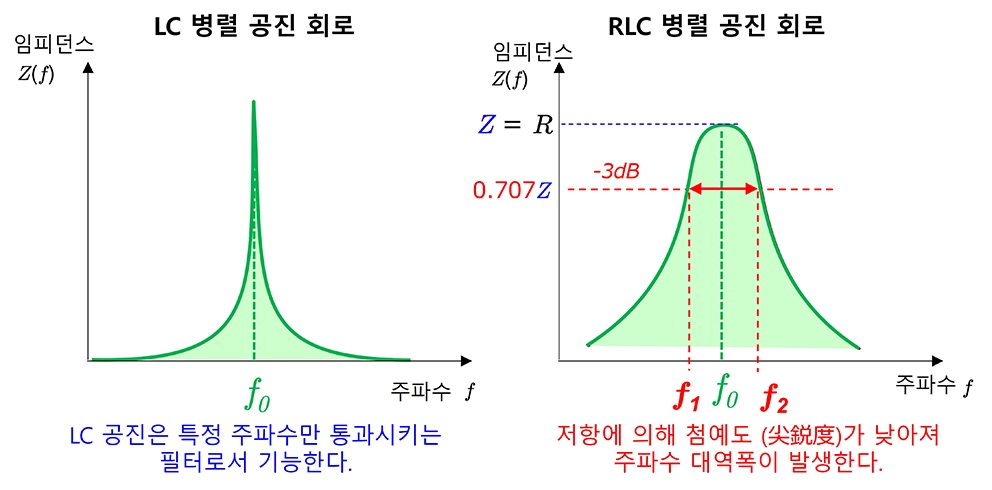
Q factor가 커지면 그래프가 뽀족한 모양이 되어 대역폭이 작아지고, Q factor가 작아지면 그래프가 완만한 모양이 되어 대역폭이 커지게 됩니다.

Summary

직렬 RLC 회로

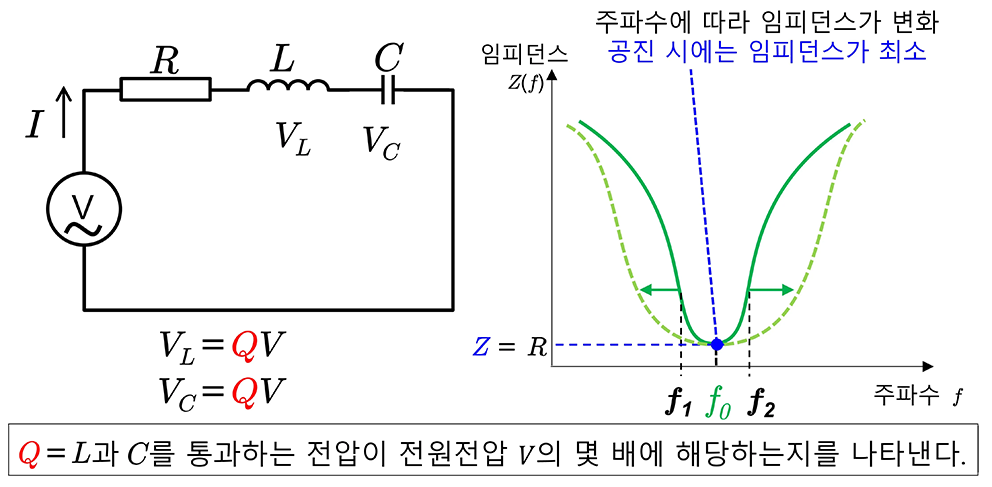
공진시 임피던스가 최소 (어드미턴스 최대)
Zin = R + jX = R + j(ωL - 1/ωC) → 최소 (리액턴스 상쇄)
Q = X0 / R , (X0 = XC = XL)
= ω0L / R = 1 / (ω0CR) = (1/R)√(L/C)

병렬 RLC 회로

공진시 어드미턴스가 최소 (임피던스 최대)
Yin = G + jB = 1/R + j(ωC - 1/ωL) → 최소 (서셉턴스 상쇄)
Q = Y / G , (Y0 = YC = YL)
= R / ω0L = ω0RC = R √(C/L)
BW = fo / Q
직렬 RLC : R/L
병렬 RLC : 1/RC