(※ 기본적인 RSA 암호 알고리즘에 대한 이해가 필요한 게시글입니다.)
(1. RSA 암호 알고리즘과 Hastad's Broadcast Attack)
(2. Common Modulus Attack)

Fermat's Factorization

개요

Fermat's Factorization (직역하자면 페르마 인수분해) 는 어떠한 두 홀수가 근접한 수일 때, 그 둘을 곱한 수에서 빠르게 두 홀수를 인수분해할 수 있는 방법이다.
이론적 배경은 아래와 같다.

Fermat's Factorization

우선, 두 소수 $p,q$의 곱으로 이루어진 $n= pq$이라는 수가 있다고 가정하자, 이 때, $n$은 당연히 홀수이다. 당연히 $p,q$ 도 소수이므로 홀수이다.
여기서 $a=\frac{1}{2}\times(p+q),\ \ b=\frac{1}{2}\times(q-p)$라고 가정하면, $p = (a-b),\ \ q = (a+b)$이다.
즉, $n=pq=(a-b)(a+b)=a^2-b^2$ 이다. 이말인 즉 $a,b$쌍을 찾으면 $n$이 인수분해 되었음을 말한다. 해당 식에서 적절히 이항을 한다면 $a^2-n=b^2$라는 식을 만들 수 있다.
여기서 $N$이상인 제곱수 $a^2$에 대해서 $a$를 $\lceil\sqrt{N}\rceil$부터 시작하여 1씩 증가시키며 $N$을 빼고, 그 값이 제곱 수가 된다면 $a$와 $b$값을 찾을 수 있으며 $a-b$와 $a+b$가 $N$의 인수가 된다는 사실을 알 수 있다.

RSA Attack?

RSA가 인수분해의 어려움에 기초해있으므로, 당연히 Fermat's Factorization이 먹히는 경우도 있다. 일정 수 이하로 $p,q$ 분포가 붙어있으면 Fermat's Factorization을 돌려서 인수분해를 끌어낼 수 있다. 무슨 말인지는 아래와 같은 경우를 생각해보자.
RSA는 $N$의 $p,q$ 인수분해의 어려움에 기초하고 있다. 만약, $N=p\times q$ 이므로 $p$ 와 가까운 소수가 $q$ 라면, 위 Fermat's Factorization을 통해서 $N=pq=(a-b)(a+b)$를 통해서 $b^2=a^2-n$ 이라는 식에서 $a$자리에 $\lceil\sqrt{N}\rceil$ 부터 브루트포스를 통해 $b$가 정수가 나오는지 유무를 통해서 인수분해 가능여부를 검사해볼 수 있을 것이다.
해당 Algorithm을 pseudo code로 나타내면 다음과 같이 나타낼 수 있을 것이다.

다만, 연산속도는 자릿수가 늘어남에 따라 기하급수적으로 늘어나게 된다.

실습

Fermat's Factorization을 수행할 수 있게끔 $p,q$의 소수 간격을 점점 늘여주면서 RSA 암호화와 복호화하는 간단한 코드를 구현하자. 해당 코드에서 소수의 간격은 sympy의 nextprime 함수에서 $2^i$ 간격 만큼 점점 늘이면서 구하는 것으로 구현했다.

우선, $i$값이 20일 때 까지는 유의미한 변화를 보이진 않는다.

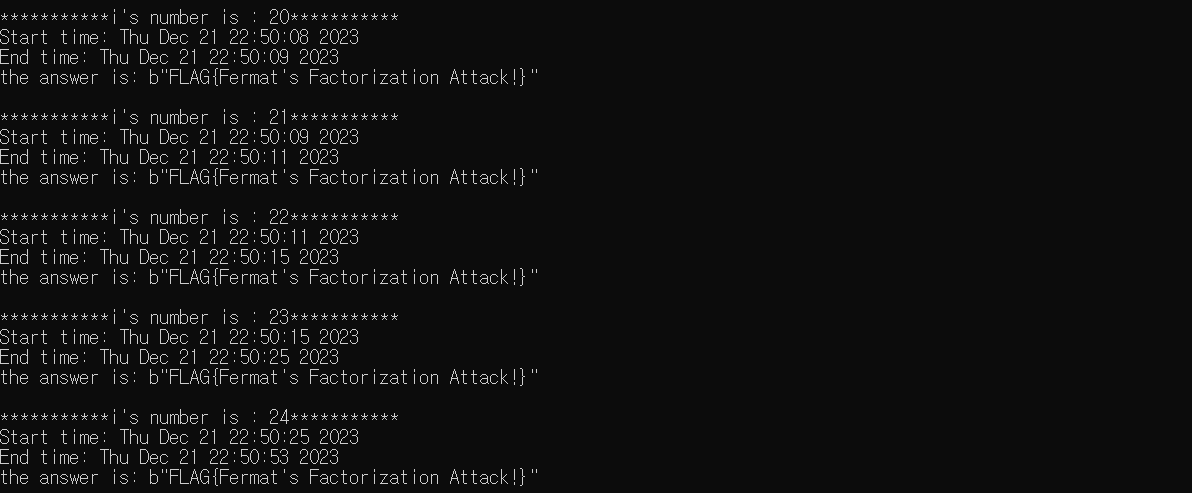
그러나 $i$값이 25를 넘어가자 연산속도는 기하급수적으로 느려지기 시작한다.

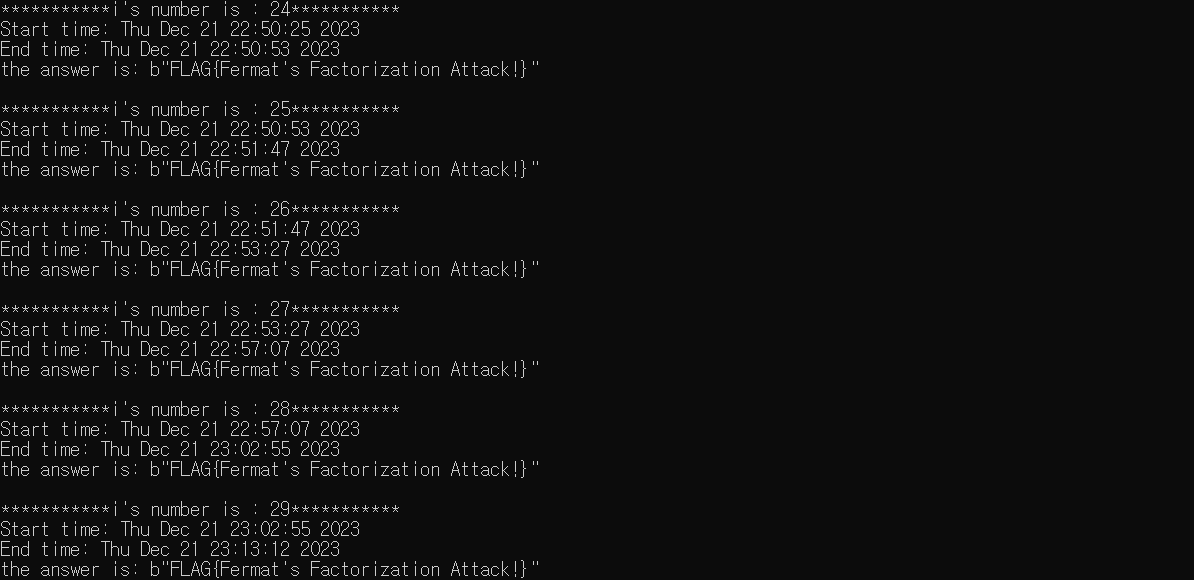
$i$값이 29에 도달하자 10분넘게 연산을 해야 해를 구할 수 있음을 볼 수 있다. 또한, $i$값이 30에 도달하면 20분가까이 연산을 해야 해를 구할 수 있다($2^{30}$정도 되면 약 10자리 정도 된다.).

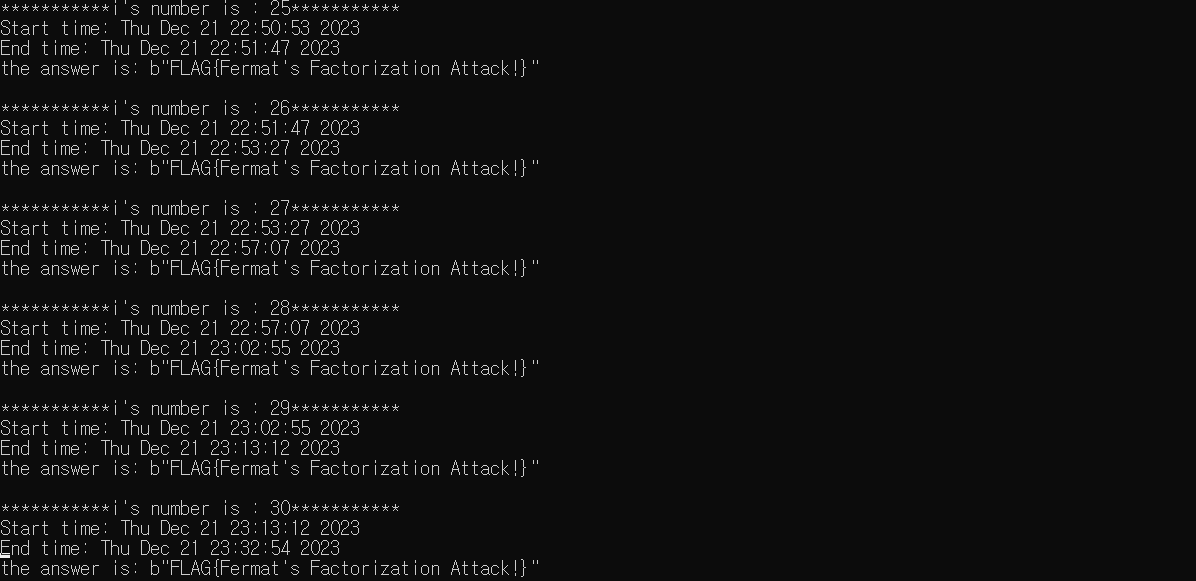
영향력?

알고리즘의 구조를 보면 알겠지만, Fermat's Factorization Method를 사용하는 것은 매우 저렴한 비용으로 행할 수 있는 공격이다.
매우 간단한 공격이라 CTF에나 잠깐씩 나올 것 같지만, 놀랍게도 최근에 해당 공격이 성공한 실사례가 있다. CVE-2022-26320 이 해당 방법으로 RSA 암호 모듈의 위험성을 발견한 사례인데, Rambus SafeZone Basic Crypto Module 의 10.4.0 이전 버전에서, 키 생성 알고리즘이 Fermat's factorization method에 의해서 깨질 위험성이 있었다고 한다. Fermat's factorization 으로 $N$을 인수분해할 수 있다면, TLS Certificate 에 있는 공개키를 통해서 private key를 쉽게 추출 ($e \equiv d^{-1}\pmod {\phi(N)}$)할 수 있다.
비록, 키 생성 로직의 미흡이긴 하지만, 1643년에 나온 Fermat's Factorization Algorithm을 1977년에 나온 RSA 암호 공격에 사용할 수 있다는 사실이 어이가 없기도 하면서 재밌기도 하다.

대처 방안

RSA key generator는 $p,q$ 라는 소수를 골라야하지만, 가까운 소수(neighboring primes)를 고르면 안된다. 일반적인 RSA의 키 크기인 2048비트를 사용하여 생성된 키는 100Round의 Fermat Factorization Attack으로 $2^{517}$까지 차이나는 숫자를 안정적으로 인수분해 한다고 한다. 즉, 하위 64바이트 내에서만 차이가 난다면 취약할 수도 있다고 한다(출처: https://fermatattack.secvuln.info/).
물론 소수가 독립적으로 무작위 생성될 경우, 취약한 키가 우연히 생성될 수 있을 확률은 $1:2^{500}$ 보다 작으므로 거의 불가능하다고 한다.

---

출처:
https://fermatattack.secvuln.info/
https://eprint.iacr.org/2023/026.pdf
https://asecuritysite.com/rsa/rsa_01
https://vulners.com/cve/CVE-2022-26320