선형대수학 - 벡터

벡터란?

• 화살표 같은 것 -> 크기와 방향이 존재한다.*
  • 벡터의 기하학적 특성을 반영 -> 특히 좌표계의 변환에 대해 불변한다.
    • 뭔소리지? 이해가 안된다. -> 축이 바뀌더라도 벡터 그 자체는 가만히 있는다.
      

위의 그림처럼 축이 바뀌더라도 벡터는 바뀌지 않는다. 다만 벡터의 성분이 변할 뿐이다.

• 숫자를 순서대로 나열한 것(리스트) -> 컴퓨터 과학적 사고

  • 차원을 늘리는데 간단함 -> 그냥 옆에 숫자 몇 개 더 적어 넣으면 됨
  • 벡터 성분이 좌표계의 변환에 대해 가변적 -> 축이 바뀌어도 성분만 바뀌고 벡터가 가르키는 방향은 그대로
    • 위의 사진을 보면 이해가 쉽다.

• 벡터 공간의 원소

  • 벡터 공간 안에 존재하는 원소
    • 먼소리지? -> 벡터 공간이 규제하는 규칙을 모두 따르며 존재하는 원소들
    • 무수히 많은 벡터들이 존재할 수 있는 공간에 존재하는 하나의 벡터로 이해할 수 있는 것 같다.
  • 벡터 공간은 세 가지 요소가 정의되고 성립되어야 한다.
    • (V(벡터), +(덧셈 규칙), ⋅(곱셈 규칙))
  • 이래도 이해가 잘 안된다. ㅋㅋㅋㅋㅋ 수학이 원래 그렇지 뭐

벡터의 기본 연산

벡터의 기본 연산은 2가지 이며 상수배, 벡터 간의 합이다.

벡터의 상수배(scalar multipliation)

말 그대로 벡터를 상수(스칼라)배 하는거다. (1, 1)의 벡터를 n(n은 상수(스칼라))배 한다면 (n, n)이 될거다

• 스칼라 (수학): 벡터 공간에서 벡터를 곱할 수 있는 양

이를 식으로 나타낸다면

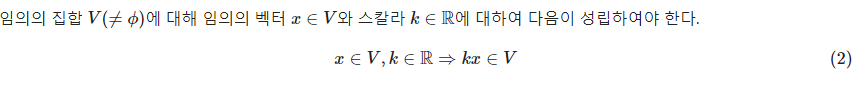
여기서 k∈R에서 R은 실수(Real number) 집합을 의미하는 것 같다.

벡터 간의 합

좌표상으로 나타내는 것이 더 쉬울 것 같다.

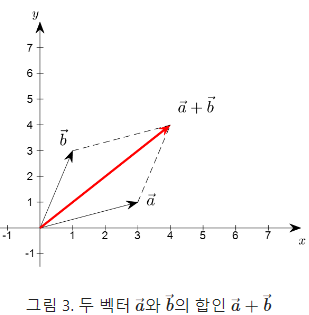
이를 식으로 나타낸다면

예시로 들자면 벡터a = (1, 3), 벡터b = (3, 1) 이 둘을 더하면 (1+3, 3+1) = (4, 4) 벡터가 생성되는 것이다.

여기서 2, 3번 식이 의미하는 것은 연산 후 결과가 여전히 벡터공간에 존재한다는 것을 나타내는 것 같다.

벡터의 기본 연산이 중요한 이유

• 벡터의 기본 연산이 잘 정의되는 것들은 선형성을 만족한다고 할 수 있기 때문
  • 선형성을 만족하는 개념들은 수학적으로 다루기가 쉽기 때문이라고 한다.
• 우리가 다루는 거의 모든 데이터는 벡터로 표현이 가능하기 때문

가장 기초적인 데이터 변형 방법

벡터를 보는 관점 중 두 번째 "숫자를 순서대로 나열한 것(리스트)" 관점에서 상수배와 벡터간의 합이 중요할 수 있다.
즉, 데이터를 벡터로 생각하여 데이터를 처리한다고 보는 관점이다.

5명의 국어, 영어 성적의 평균을 계산한다고 생각해보자.
국어 성적을 벡터로 표현하면 다음과 같다.

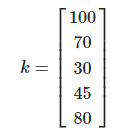
영어 성적을 벡터로 표현하면 다음과 같다.

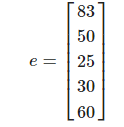
이 두 점수들을 평균 내는 방법은 다음과 같다.

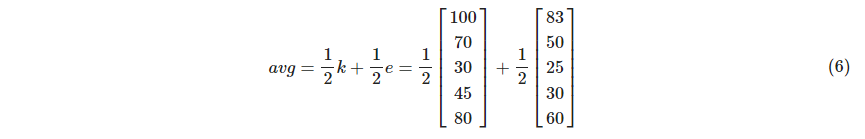
AI를 공부하는 입장에서 이 관점이 매우매우 중요할 것임이 느껴진다.
학습 데이터들을 대부분 벡터로 표현할 수 있기 때문이다.

벡터간의 선형 결합

벡터간의 선형 결합을 표현하기 위해 벡터의 기본 연산은 선행 조건이다.
상수배와 벡터간의 합을 한 번에 활용하면 임의의 두 벡터에 대한 선형 결합을 표현할 수 있다.

선형 결합은 상수배와 벡터간의 합을 한번에 조합해 표현한 것이다.

선형 결합이 왜 중요하지? -> c1과 c2는 각각 모든 실수가 될 수 있다. -> c1, c2가 변경됨에 따라 벡터공간 내 모든 벡터에 대응된다.
-> 벡터공간이 생성된다.

이처럼 벡터 간의 선형 결함이 어떤 벡터공간 전체에 대응된다는 개념을 공간 생성(span) 이라고 한다.

행렬곱과 연립방정식의 해를 얻는 과정에 대한 새로운 관점을 재시해줄 아주 중요한 단서가 된다고 한다.

Ref : https://angeloyeo.github.io/2020/09/07/basic_vector_operation.html

이 공돌이의 수학정리노트는 정말 엄청나다.
원래부터 수학이 배우고 싶었지만 어떻게 시작해야할 지 모를 때 보면 좋은 것 같다.
선행지식이 조금 필요한 것 같지만 이정도는 괜찮아 보인다... 지금은?