수정 : 아래 그림이 미리보기로 나와서 보기에 좋지않아 사진 하나 올린다.
직접 찍은 사진이다. (위치는 이스탄불)
PCA(주성분 분석)이란 무엇인가?
-
정의
이미지 데이터(100*100) or 한 자동차의 특성 데이터처럼 여러 개의 열을 가진 데이터(다차원 데이터)를 저차원의 데이터로 환원시키는 기법 -
쓰는 이유
다차원 데이터의 분포를 가장 잘 표현하는 성분들을 추려내기 위함
-> ?? 먼소리임
-> 예시를 들어보자 -> 100 X 100의 이미지를 10000개의 원소를 가진 1차원 배열이라고 생각해보자. 이러한 이미지가 10,000개, 100,000개 있다고 한다면 이걸 저장하고 학습하는데 문제가 생길 수 있다.
이 100 X 100의 이미지 중 모든 이미지들을 잘 표현하는 사진들의 특징을 종합하여 추려내는 것이 좋을 것이다.
-> ??? 먼소리지 -> 사진으로 봐보자

출처 : https://darkpgmr.tistory.com/110각 사진들에서 k가 작아질수록 거의 똑같아 지는 것을 볼 수 있다.
이처럼 각 이미지들을 잘 나타내는 성분들을 고르는 것이다. -> 이미지는 각 이미지들을 합성한 후 잘 나타내는 것을 고르는 느낌으로 이해하면 될 것 같다. -
특징
-
주성분의 차원수는(데이터 수)는 원래 데이터의 차원수보다 작거나 같다.
-
데이터를 한 개의 축으로 정사영시켰을 때 차원 축소가 일어나고 이때 축소는 데이터의 분산이 가장 커지는 축(PC1)을 기준으로 일어난다.
-
두 번째로 커지는 축을 두 번째 주성분(PC2)으로 놓이도록 새로운 좌표계로 데이터를 선형 변환시킴
2번 특징을 생각해보자
정사영 시킬 때 차원 축소가 일어난다. -> ??????
-> 3번 특징과 연관지어 생각할 수 있다.
PC2를 정하고나서 PC1과 PC2를 하나의 좌표계로 생각하고 거기에 사영시켜 차원을 줄인다.
-> ??? -> 그림을 보자
간단하게 2차원에서 1차원으로 변환시키는 것을 생각해보자
원본 데이터의 모습은 아래의 그림과 같다.
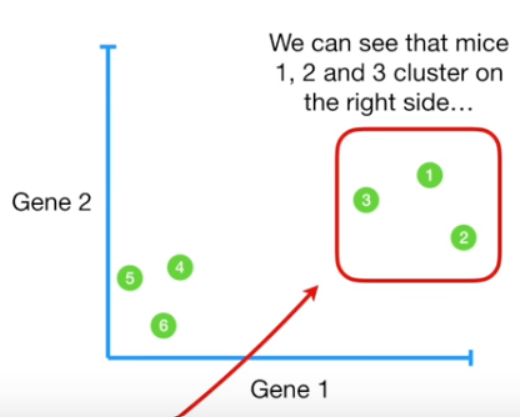
원래 (0, 0)이 기준이었던 좌표에서 각 점들의 중앙값이 기준이 되는 좌표로 넘어와보자.
그럼 아래 그림과 같을 것이다
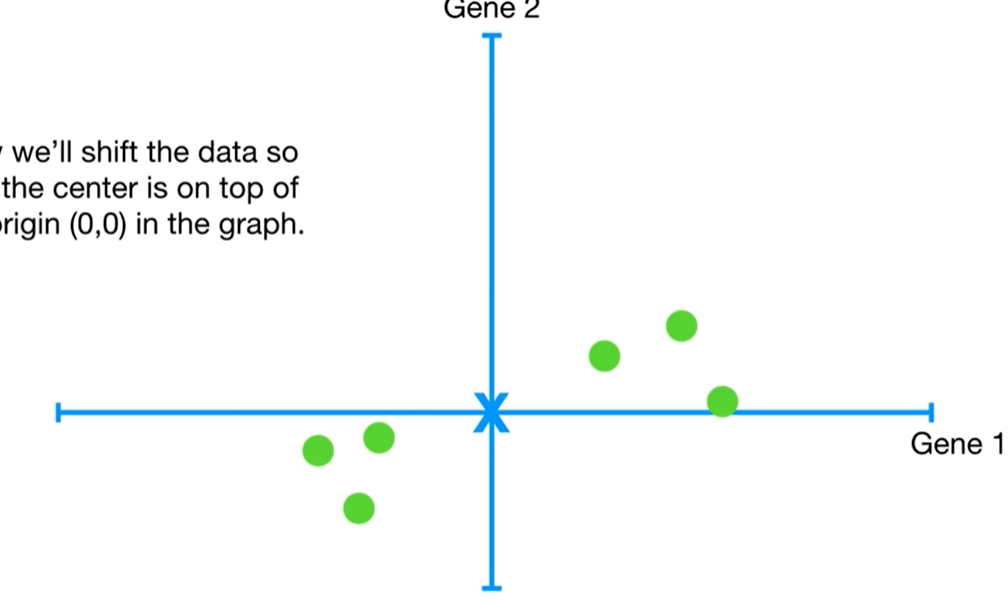
이제 차원축소를 위해 이 데이터들을 가장 잘 설명하는(데이터의 손실이 가장 적은) 직선을 찾을 것이다. 이때 '데이터들을 가장 잘 설명하는' 이라는 말은 '데이터들을 한 직선에 정사영 시켰을 때 분산이 가장 큰' 과 같은 말이다.
-> ???
-> 분산은 데이터가 중앙과 얼마나 멀리 떨어져 있는지를 알 수 있는 수치이다.
-> 분산이 크면 왜 데이터들을 가장 잘 설명하나요?
-> 분산이 크다는 것은 데이터가 정사영 될 때 직선과 각 점사이의 거리가 가장 적다는 것이다.
-> 정사영 시킬 때 직선과 각 점사이의 거리만큼 손실이 발생하기 때문
-> 아하! 라고 이해했지만 아니라면 댓글로 알려주시면 감사하겠습니다 :)
자 그럼 그런 직선을 찾아보자
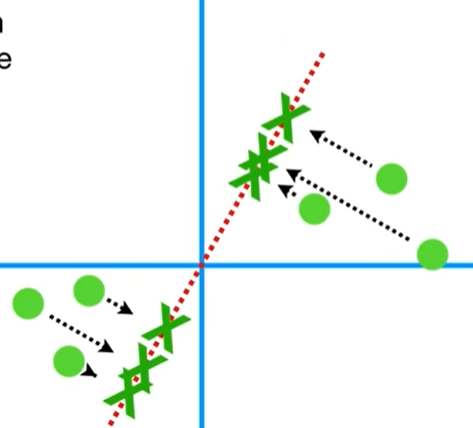
이 그림을 보면 저 직선이 정사영시켰을 때 데이터가 떨어져 있는 정도가 가장 큰 직선이라고 할 수 있을까?
아니다. 아래 그림을 보면 이해가 갈 것이다.
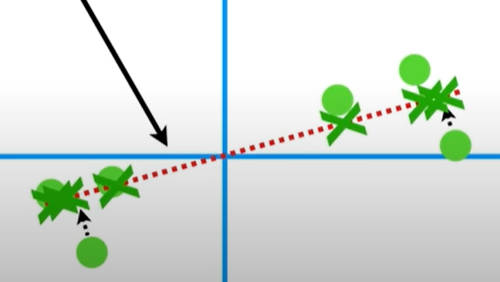
이처럼 더욱 데이터들끼리의 거리가 멀게 설정할 수 있다.
이 때 이 직선이 PC1이 된다.
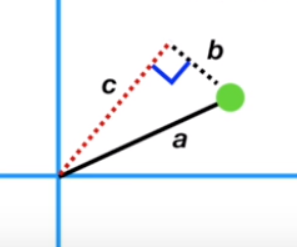
이 그림에서 a는 원점에서 점까지의 거리, c는 PC1, b는 점을 PC1에 정사영 시킬 때 생기는 직선이다.
직각삼각형 이기 때문에 a^2 = b^2 + c^2 이므로 c가 커지면 b는 작아지고 b가 커지면 c가 작아진다. b와 c는 반비례관계이다.
이 때 PC1은 c가 최대가 되거나 b가 최소가 되는 그 직선이 된다.
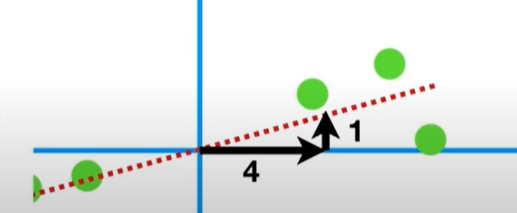
이 때 이 직선의 기울기를 0.25(1/4)라고 했을 때 x축이 4번 움직이면 y축은 1번 움직인다.
이런 기울기를 x축과 y축의 선형결합이라고 한다. 이 때 x, y는 각 특성이 될 것이다.
-> 선형대수에서 선형결합이 먼소리인지 몰랐는데 이걸 보니 이해가 된다.
참고 : https://velog.io/@hunterhunter/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99-%EB%B2%A1%ED%84%B0
이 때 이 선의 기울기를 기저벡터(기준 축)으로 잡는데 그림으로 보자.

이 때 기울기를 피타고라스 법칙을 이용해 구하고 기울기로 나누어 1로 만들어준다. -> 기저벡터(기준 축) 생성
그리고 이 직선에 데이터들을 정사영 시키면 한 직선위에 모든 점들을 표현이 가능할 것이다.
2차원 직선상에 2차원 점들을 정사영시키면 직선 상에 모두 표현이 가능해지는 것 이게 차원 축소이다.
이제 처음에 본 이미지로 다시 이미지 PCA를 보자

여기서도 k=20일 때는 총 데이터개수와 같기 때문에 아래의 사진이 모두 위와 같다.
k=10일 때는 20일때 만큼 자세하지는 않지만 꽤나 비슷하다고 볼 수 있다.
그러나 k=5일 때 부터 점점 이미지가 같아지고 있다.
이는 k=2일 때가 가장 심한데 이는 차원을 계속 축소하는 과정에서 손실이 발생하기 때문에 원래 얼굴들이 사라지는 것 같다.
그리고 PCA를 할 때 노이즈가 있다고 들었는데 뭔지 몰라서 2편에서 다뤄보도록하겠다.
이제 코드로 한 번 확인해보자.
http://matrix.skku.ac.kr/math4ai-intro/W12/ 에서 예시로 든 과정을 들고 와봤다.
-> 이 부분은 SVD(특이값 분해)를 이해하고 진행해야할 것 같아 남겨두겠다.
-> 이것도 2편에서
Ref : https://www.youtube.com/watch?v=FgakZw6K1QQ&ab_channel=StatQuestwithJoshStarmer
이 영상이 설명을 잘 해준다.

