📌 다익스트라(Dijkstra) 알고리즘이란?
다익스트라 알고리즘은 두 정점 사이의 최단 경로를 구할 때 사용되는 가장 대표적인 탐색 알고리즘입니다. 다익스트라 알고리즘은 두 정점 사이의 최단 경로 이외에도 출발 정점으로부터 모든 정점까지의 최단 경로를 구하는 알고리즘입니다. 다익스트라 알고리즘에 들어가기에 앞서 최단경로의 정의와 최단경로의 특성에 대해 짚고 넘어가도록 하겠습니다.
다익스트라 알고리즘은 출발 정점으로 부터 다른 정점까지의 최단 경로를 구할 때, 유용한 알고리즘이다.
📌 최단경로 ( Shortest - Path )
최단경로란?
가중치 그래프 G = ( V, E, W ) 가 존재할 때, 정점 x 부터 정점 y까지의 어떤 경로 P의 가중치인 W(P)가, 정점 x로부터 y까지의 경로 중에서 가장 작을 때 P를 최단 경로라고 합니다. 간단하게 이야기하면, 두 정점 사이의 존재하는 경로중에 가중치가 가장 작은 경로를 최단경로라고 합니다.
최단경로의 특성
"어떤 최단경로는 최단경로들로 구성되어 있다."
정점 x에서 출발하여 정점 z까지 도착할 때, 존재하는 최단경로는 (정점x부터 정점 y까지의 최단경로) + (정점 y부터 정점 z까지의 최단경로)와 같습니다. 즉, 정점에서 정점까지 최단경로를 구할 때, 이전에 구했던 최단 거리 정보를 사용한다는 특징이 있습니다. 큰 문제를 해결할 때 작은 문제를 먼저 해결하는 Dynamic Programming의 특징을 가지고 있습니다.
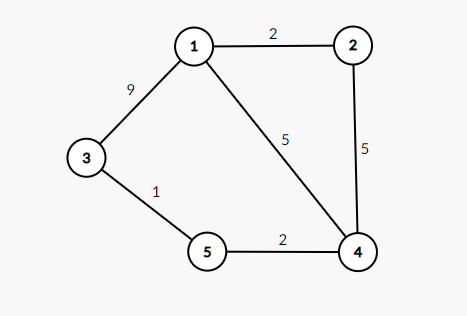
예를 들어, 1번부터 5번까지의 최단경로는 1번부터 4번까지의 최단경로와 4번부터 5번까지의 최단경로의 합이 됩니다.
📌 다익스트라 알고리즘의 최단경로
다익스트라 알고리즘의 작동 방식은 다음과 같습니다.
1. 모든 정점의 방문 정보를 초기화 합니다.
2. 정점 중 출발점을 선택합니다. 출발점은 Tree Set에 저장하고, 그와 인접한 정점의 정보를 Fringe Set에 저장합니다.
3. Fringe Set에서 최소값을 갖는 정점을 Tree Set에 추가하고, 그 정점의 인접한 정점의 정보를 Fringe Set에 업데이트 합니다.
- 업데이트 방식은 새로운 정점 정보가 들어오면 추가하고, 기존에 정점 정보가 이미 있다면, 가중치가 작은 경우에만 업데이트 합니다.
4. 그래프의 모든 정점이 Tree Set으로 전환될 때 까지 3번의 과정을 반복합니다.
* fringe set / vertex : 인접한 정점들 중 아직 방문하지 않은 정점을 의미합니다.예시를 보겠습니다.
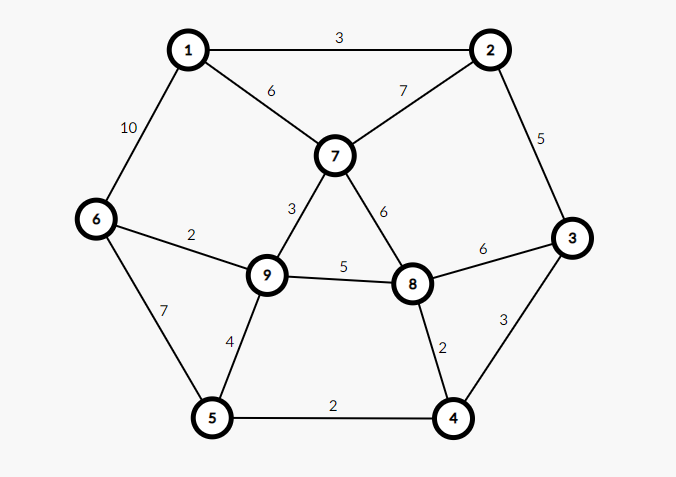
다음 그래프에서 시작점을 1로 했을 때, 출발점인 1은 Tree Set이 됩니다. 그와 인접한 2번, 6번, 7번은 Fringe Set이 됩니다.
왼쪽 영역 : Tree Set / 오른쪽 영역 : Fringe Set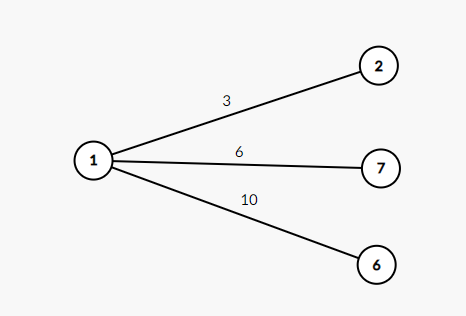
Fring Set에서 가중치가 가장 작은 정점을 선택해야 합니다. 따라서 2번 정점이 Tree Set에 추가가 됩니다. 이후에 2번 정점과 인접한 정점들은 Fringe Set에 업데이트 됩니다.
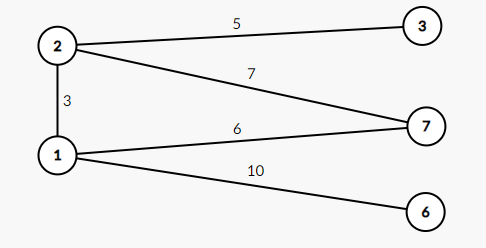
1번과 2번 정점 모두 7번과 인접합니다. 이런 경우에 Fringe Set에는 가중치가 작은 정점을 선택하여 업데이트 됩니다. 따라서 2번과 7번의 간선정보는 저장하지 않고 1번과 7번 간선정보만 저장하게 됩니다.
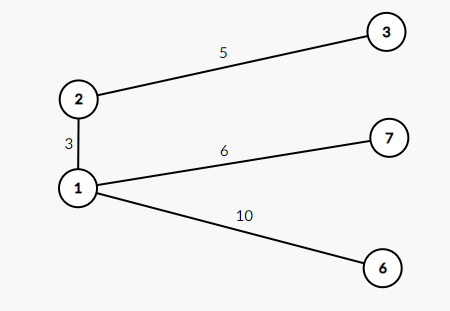
위와 같은 과정을 반복하면 모든 정점을 방문하게 되고, 다익스트라 알고리즘을 모두 수행하게 됩니다.
📌 다익스트라 알고리즘 분석
다익스트라 알고리즘은 모든 정점을 방문해야 합니다. 따라서 N번의 수행이 필수적이고, Heap 구조를 이용하면 logn에 탐색을 할 수 있습니다. 결과적으로 다익스트라 알고리즘의 시간 복잡도는 O(N * logn)이 됩니다.
.png)
📌 마무리
오늘은 최단경로를 구할 때, 사용하는 알고리즘 중 하나인 다익스트라 알고리즘에 대해 알아보았습니다. 인접리스트와 인접행렬 구현에 따라서 시간복잡도가 달라지기 때문에, 간선 정보가 적을 때는 인접리스트로 구현하는 것이 유리한 방법이겠습니다.
