📌 최장 증가 부분 수열(LIS)이란?
LIS(Longest Increasing Subsequence)는 가장 긴 증하는 부분 수열입니다.
이해를 위해 예시를 보겠습니다.

다음과 같은 수열이 존재합니다. 이 때, 여기서 최장 증가 부분 수열을 찾으면

이미지와 같이 파란색으로 색칠된 부분이 최장 증가 부분 수열이 됩니다.
즉 최장 증가 부분 수열이란, 전체 수열에서 앞에서부터 뒤로 숫자를 선택하여 부분 수열을 생성할 때, 숫자가 증가하면서 그 부분 수열의 크기가 최대가 되는 수열입니다. 최장 증가 부분 수열을 DP를 이용하여 구현하면 O(N^2)의 시간복잡도를 가집니다.
DP[i] : i번 째 수를 부분 수열의 마지막 원소로 갖는 LIS의 길이
📌 DP를 이용하여 LIS 구현하기
DP를 이용하여 수열의 맨 앞부터, 맨 뒤까지 index를 증가시키며 확인해야 하기 때문에 이중 반복문 즉, O(N^2)의 시간복잡도를 갖는다.
.png)
DP를 이용하여 LIS를 구현하는 것은 이중 포문을 이용하기 때문에 구현이 쉬운 강점이 있습니다. 그러나 제곱의 시간복잡도를 갖기 때문에 N의 값이 커지게 되면 해당 알고리즘을 정해진 시간안에 출력하기 어렵습니다. 따라서 분할 정복을 이용하거나 세그 먼트 트리를 이용하여 O(NlogN)의 시간복잡도를 이용해야 합니다.
📌 분할 정복을 이용하여 LIS 구현하기
lower_bound를 이용하여 최솟값을 추적하여 구현하면 시간에서 이득을 볼 수 있습니다. 수열의 처음부터 끝부분까지 확인하는 방법은 같습니다. 이후에 lower_bound를 이영하여 LIS를 유지하기 위해 최적의 위치에 수를 삽입합니다. 이해를 위해 예시를 보겠습니다.
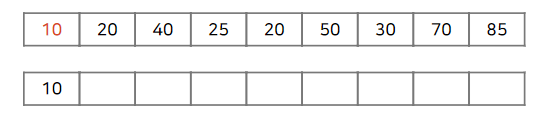
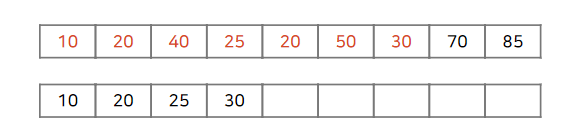
수열의 앞부분부터 시작합니다. 빨간색의 수가 LIS 마지막의 최솟값보다 작으면 삽입합니다.
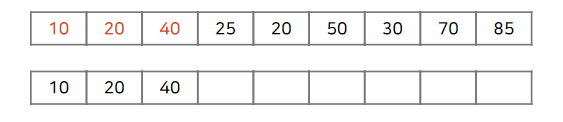
40까지는 벡터의 마지막값보다 수열 진행 부분의 수가 더 크기 때문에 그대로 삽입합니다.
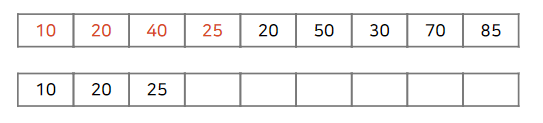
25는 벡터의 마지막 값보다 작습니다. 벡터의 lower_bound를 추적하여 25를 적당한 위치에 삽입합니다.
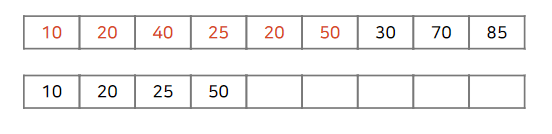
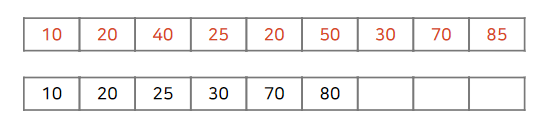
최종적으로 수열의 끝부분에 도착하면 벡터의 길이를 통해 LIS의 길이를 알 수 있게 됩니다.
.png)
📌 최장 증가 부분 수열(LIS) 분석
최장 증가 부분 수열을 확인하기 위해서는 배열의 처음부터 끝까지 탐색이 필요합니다. 이후에 DP로 구현하거나 Lower_bound를 이용하여 구현할 수 있습니다. 두 구현 방법 모두 어렵지 않기 때문에 시간복잡도에서 강점을 갖는 Lower_bound로 구현하는 것이 좋습니다.
DP로 구현한 LIS의 시간복잡도 : O(N^2)
Lower_bound로 구현한 LIS의 시간복잡도 : O(NlogN)
📌 마무리
오늘은 부분 수열 중 하나인 최장 증가 부분 수열에 대해 알아봤습니다. PS에서 가끔 등장하는 문제이기에 알아두면 유용한 부분 수열입니다. 다음에는 최장 공통 부분 수열(LCS)와 최장 공통 문자열에 대해 알아보도록 하겠습니다.
