[ML] Gradient Descent, Evaluation, Generalization Error, Overfitting

Yeon·2023년 12월 2일

ML

목록 보기

3/7

Gradient Descent

경사 하강법(Gradient Descent)은 머신 러닝과 딥러닝에서 손실 함수(Loss Function)을 최소화하여 모델의 파라미터를 찾는 데 사용됩니다.

목표(Objective):
선형 회귀 모델에서 목표는 손실 함수 $J(\mathbf{w}, \mathbf{D})$ 를 최소화하는 것입니다. 여기서 $J(\mathbf{w}, \mathbf{D})$ 는 모델 예측과 실제 관측값 사이의 평균 제곱 오차(Mean Squared Error, MSE)입니다.
$J(\mathbf{w}, \mathbf{D}) = \frac{1}{N} \sum_{n=1}^{N} (y^{(n)} - f(\mathbf{x}^{(n)}, \mathbf{w}))^2$
여기서 $\mathbf{w}$ 는 가중치 벡터, $\mathbf{x}^{(n)}$ 는 n번째 데이터 포인트, $y^{(n)}$ 은 n번째 데이터 포인트의 실제 값입니다.
경사 하강법(Gradient Descent):
경사 하강법은 손실 함수의 그라디언트(미분)를 계산하고, 이 그라디언트가 감소하는 방향으로 가중치를 조정하는 방법입니다.
$\mathbf{w} \leftarrow \mathbf{w} - \alpha \nabla_{\mathbf{w}} J(\mathbf{w}, \mathbf{D})$
여기서 $\alpha$ 는 학습률(learning rate)로, 각 반복에서 가중치를 얼마나 조정할지 결정합니다.
👉 $\alpha > 0$ 이렇게 하지 않으면 알고리즘 자체에서 부호를 바꿔줘야 하는 문제가 발생할 수도 있다.
가중치 업데이트 규칙:
각 가중치 ( w_i )에 대해, 다음과 같은 업데이트 규칙을 사용합니다.
$w_i \leftarrow w_i - \alpha \frac{\partial}{\partial w_i} J(\mathbf{w}, \mathbf{D})$
여기서 $\frac{\partial}{\partial w_i} J(\mathbf{w}, \mathbf{D})$ 는 손실 함수를 $w_i$ 에 대해 편미분한 값입니다.
편미분(Derivatives):
손실 함수의 $w_i$ 에 대한 편미분은 다음과 같이 주어집니다.
$\frac{\partial}{\partial w_i} J(\mathbf{w}, \mathbf{D}) = -\frac{2}{N} \sum_{n=1}^{N} (y^{(n)} - f(\mathbf{x}^{(n)}, \mathbf{w})) x_i^{(n)}$
이 편미분은 손실 함수의 감소하는 방향을 나타내며, 경사 하강법에서는 이 방향으로 가중치를 조정합니다.

경사 하강법은 각 반복마다 전체 데이터 세트(또는 데이터 세트의 일부)를 사용하여 가중치를 업데이트합니다. 이 방법은 데이터 세트가 매우 크거나 해석적 해를 찾기 어려울 때 유용합니다. 경사 하강법은 보통 여러 반복을 거쳐 점진적으로 최적의 가중치에 수렴하게 됩니다.

간단한 작동 원리
- 랜덤한 지점(Initialization)을 하나 찍습니다.
- 이 지점에서의 에러를 확인합니다.
- 에러를 미분합니다.
- 에러의 방향에 따라서 w를 어떻게 조절을 해줘야 할지에 대한 것이 Gradient Descent 입니다.
- 미분한 값이 기울기가 음수이면 양의 방향으로 이동하면 되고, 기울기가 음수이면 음의 방향으로 이동하면 됩니다.
linear regression 에서는 Gradient Descent로 풀었을 때 언제나 정답이 나옵니다. 최적화 문제에 있어서 actual solution(=Global Optimum : 내 parameter 구간 전체에서 최적점이 내가 찾은 점이다) 라는 것을 의미합니다. 또한, minimum이 한 개이기 때문에 찾기 쉽습니다. 그러나 일반적인 Regression 모델에서는 한 개 이상이 나올 수도 있습니다. (Eg. neural nets). 일반적인 Regression 모델의 경우엔 Evaluator를 가지고 각 지점에 대해서 검증을 해봐야 하는 것이다.
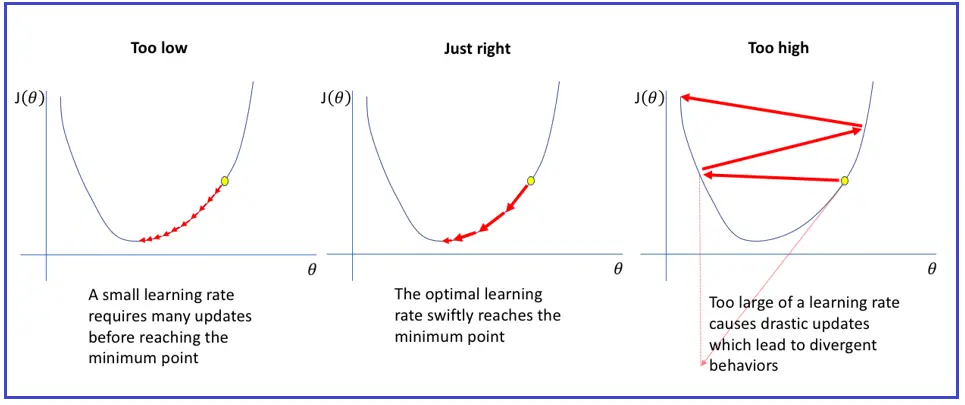
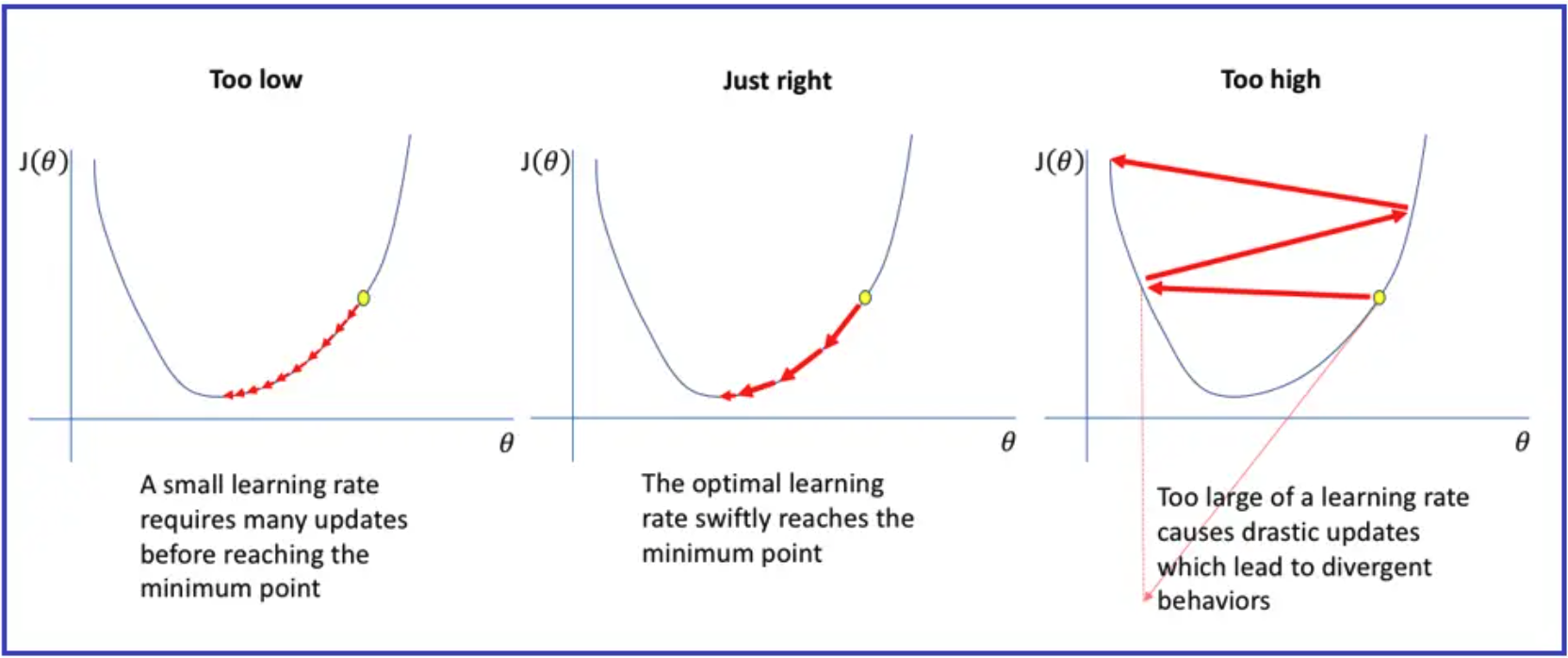
Learning rate
Learning rate( ${\alpha})$ 가 크면 더 빨리 학습이 되고, convergence가 빨라집니다. 하지만, 너무 크게 되면은 Fitting이 되지 않고, 계속 왔다갔다만 진행될 수 있습니다. 이것을 Oscillation이라고 말합니다.

Evaluation

이미지에는 선형 회귀 모델을 평가하기 위한 세 가지 주요 지표가 나와 있습니다:

RSS (Residual Sum of Squares):
RSS는 모델의 예측값과 실제 데이터 값 사이의 오차의 제곱합입니다. 이는 모델이 데이터를 얼마나 잘 적합하는지를 나타내는 척도로 사용됩니다.
$RSS(\mathbf{w}) = \sum_{n=1}^{N} (y^{(n)} - \mathbf{w}^T \mathbf{x}^{(n)})^2$
여기서 $y^{(n)}$ 은 실제 값, $\mathbf{w}^T \mathbf{x}^{(n)}$ 은 모델에 의한 예측값입니다.
RMSE (Root Mean Squared Error):
RMSE는 RSS를 데이터 포인트의 수 $N$ 으로 나눈 뒤, 제곱근을 취한 값입니다. 이는 평균적인 오차의 크기를 나타내며, 모델의 성능을 쉽게 해석할 수 있는 형태로 제공합니다.
$RMSE(\mathbf{w}) = \sqrt{\frac{1}{N} RSS(\mathbf{w})}$
R² (Coefficient of Determination):
R²는 모델이 데이터의 변동성(variability)을 얼마나 잘 설명하는지를 나타내는 지표입니다. 값이 1에 가까울수록 모델이 데이터를 더 잘 설명한다는 것을 의미합니다.
$R^2 = 1 - \frac{RSS(\mathbf{w})}{TSS}$
여기서 TSS(Total Sum of Squares)는 실제 값의 분산에 대한 총합으로, 다음과 같이 계산됩니다:
$TSS = \sum_{n=1}^{N} (y^{(n)} - \bar{y})^2$
$\bar{y}$ 는 실제 값 $y^{(n)}$ 의 평균입니다.

모델의 Generalization Error

모델 훈련: 모델은 과거 데이터 $D$ 를 기반으로 학습되며, 이 데이터는 모델의 파라미터를 적합시키기 위해 사용됩니다. 모델을 훈련시키는 과정에서 계산되는 오차를 훈련 오류(training error)라고 하며, 이는 다음과 같이 정의됩니다:
$\text{Error}(D, a, b) = \frac{1}{N} \sum_{n=1}^{N} (y^{(n)} - f(x^{(n)}))^2$
여기서 $f(x^{(n)})$ 는 모델에 의한 예측값이고, $y^{(n)}$ 은 실제 값입니다.

일반화 오류: Training error는 모델이 훈련 데이터에 얼마나 잘 적합하는지를 나타냅니다. 그러나 우리가 실제로 관심을 가지는 것은 모델이 새로운, 보지 못한 데이터에 대해 얼마나 잘 동작하는지에 대해 오류를 계산하는 것을 의미합니다. 하지만, 이 오류를 정확히 계산하는 것은 불가능합니다. 대신, 표본 평균을 사용하여 이론적인 평균 오류를 근사치로 계산합니다.
$\text{Error}(a, b) = \mathbb{E}_{(x,y)} \left[ (y - f(x))^2 \right]$
이 식에서 $\mathbb{E}_{(x,y)}$ 는 전체 모집단(population)에 대한 기대값을 나타냅니다. 이 오류는 모델이 전체 데이터 분포를 얼마나 잘 캡처하는지를 나타내며, 이론적으로는 모든 데이터 포인트에 대한 평균 제곱 오차(mean squared error)입니다.

훈련 오류와 일반화 오류의 관계: Training Error는 일반화 오류를 근사하는 것으로 간주되지만, 항상 좋은 일반화를 보장하지는 않습니다. 모델이 훈련 데이터에 과적합(overfitting)되어 있으면, Training Error는 낮을 수 있지만 일반화 오류는 높을 수 있습니다. 반대로, 모델이 훈련 데이터에 과소적합(underfitting)되어 있으면, 두 오류 모두 높을 수 있습니다.

결국, 우리는 모델이 새로운 데이터에 대해 잘 동작하도록 만드는 것, 즉 좋은 일반화 성능을 가지도록 하는 것이 목표입니다. 이를 위해 교차 검증(cross-validation), 규제화(regularization)와 같은 기법을 사용하여 모델의 일반화 능력을 향상시킬 수 있습니다.

Overfitting

Training Error가 낮고 일반화 오류가 높은 상황을 의미한다.

Model with a large number of parameters(degrees of freedom)
- 모델에 파라미터가 많으면, 모델은 훈련 데이터의 노이즈까지 학습하는 경향이 있습니다. 즉, 모델이 너무 복잡해서 데이터의 임의의 변동성까지 반영하게 되어, 새로운 데이터에는 존재하지 않을 경우 잘못된 예측을 하게 됩니다.
Small dataset size (as compared to the complexity of the model)
- 데이터셋이 모델의 복잡도에 비해 작을 경우, 모델은 데이터에 있는 작은 패턴이나 노이즈에 overfitting이 발생할 수 있습니다. 충분히 큰 데이터셍의 경우에는 모델은 데이터의 실제 구조를 더 잘 학습하고 노이즈를 무시할 가능성이 높아집니다.

모델의 파라미터가 복잡하다 ???

모델의 파라미터가 복잡하다는 것은 모델에 많은 수의 자유도(즉, 조정할 수 있는 파라미터)가 있다는 것을 의미합니다. 이는 모델이 데이터의 미묘한 패턴을 포착할 수 있을 만큼 유연하지만, 그 결과로 노이즈나 데이터의 무작위 변동성까지 학습할 위험이 있습니다. 이는 오히려 모델이 실제로 중요한 신호보다는 데이터 내의 무작위 변동성에 과적합되게 만들 수 있으며, 이것이 overfitting의 원인이 될 수 있습니다.

data $D$ 를 Training set과 Test set으로 나눈다.

일반적으로 7:3이나 8:2의 비율로 나눈다.
Training set으로 모델을 학습시킨 뒤 Test set으로 모델을 검증한다.
🚫주의할점
- model을 학습하는 동안에는 절대로 Testing data를 건드려서는 안된다.
- 즉 Testing data는 final evaluation에만 사용되어야 한다.

Evaluation Measures

Underfit

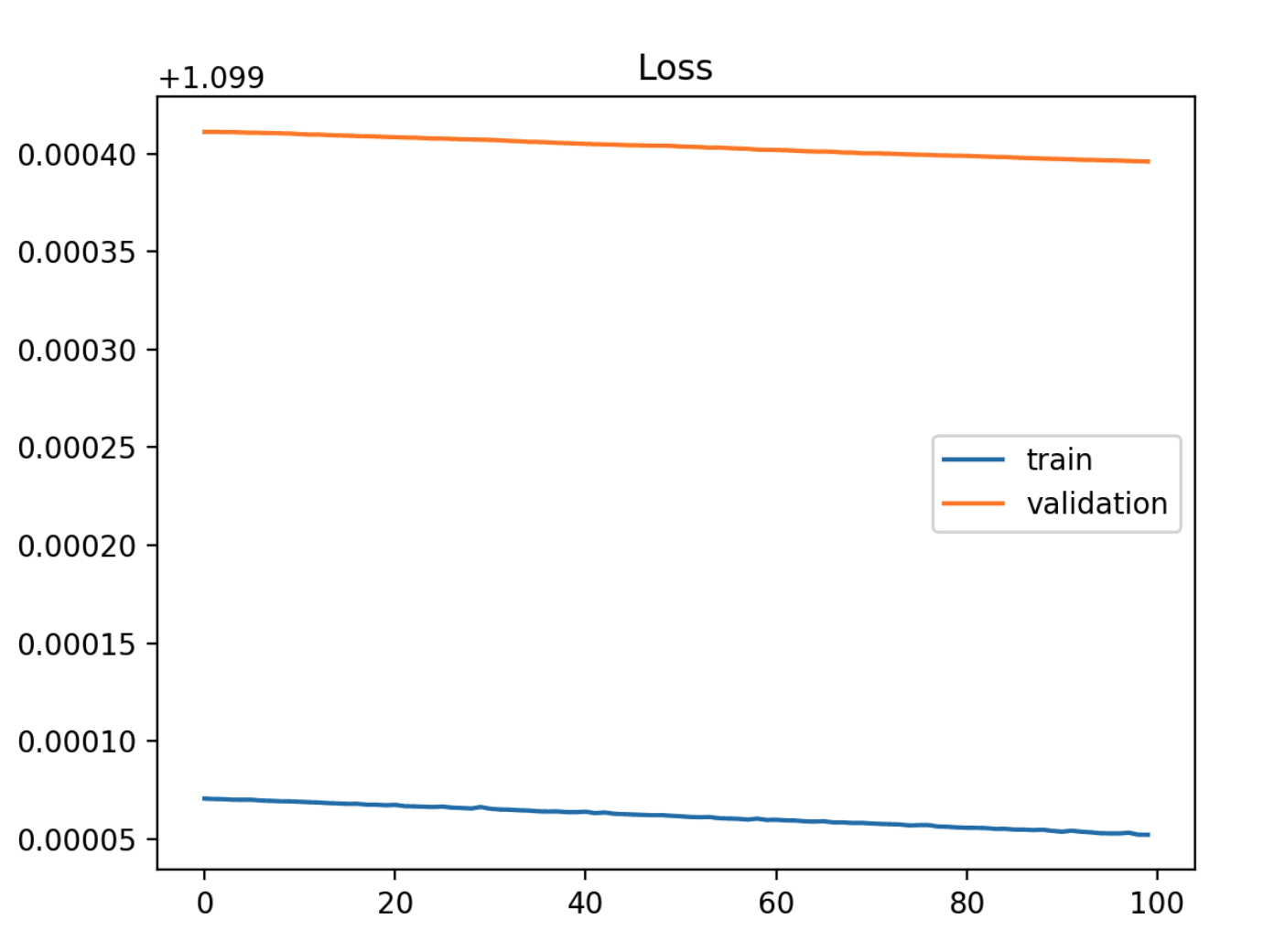
Training loss가 감소하고 있으며 Plot이 끝날 때까지 계속 감소하고 있는 모습을 확인할 수 있다. validation loss와는 많은 차이가 나기 때문에 underfit이라고 생각할 수 있다.

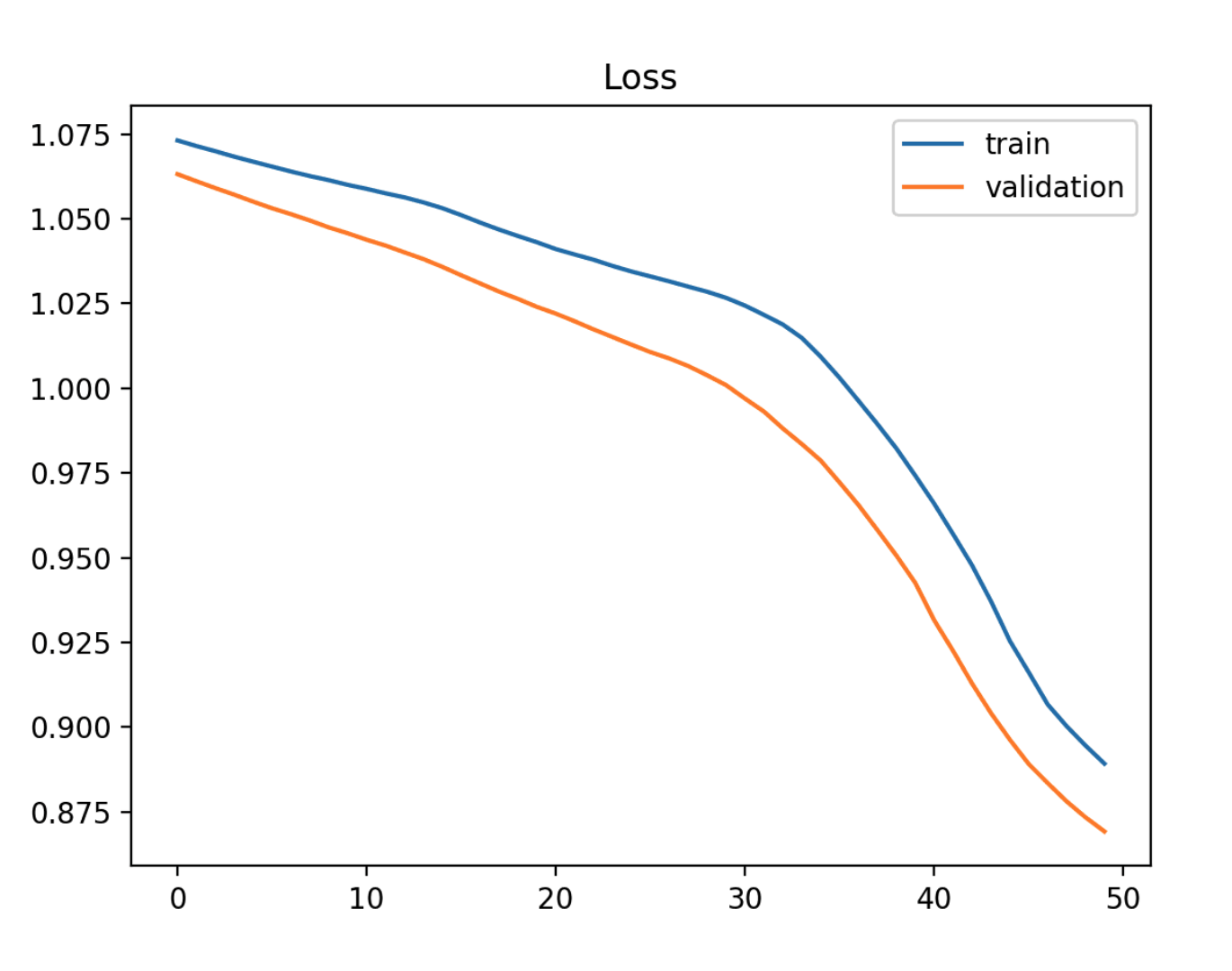
Training loss가 training에 관계없이 일정하게 유지됩니다.
Training loss가 training이 끝날 때까지 계속 감소합니다.

Overfit

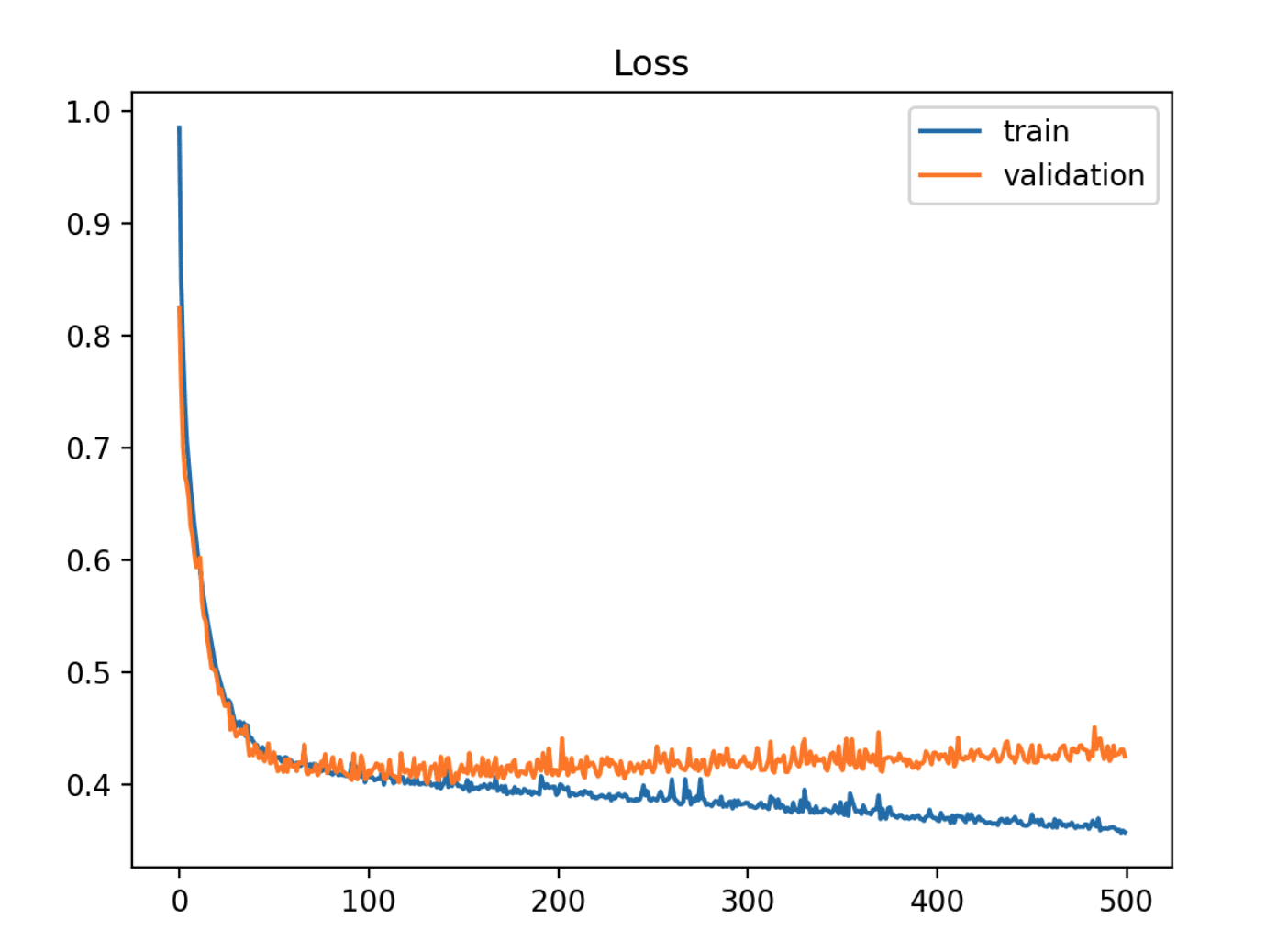
Training loss가 경험에 따라 계속 감소합니다.
Validation loss가 한 지점까지 감소했다가 다시 증가하기 시작하는 경우
Validation loss의 변곡점은 그 이후의 경험이 overfitting의 증거가 될 수 있기 때문에 중단할 수 있는 지점일 수 있습니다.
Training loss와 validation loss 사이의 간격이 시간이 지남에 따라 벌어지지 않는다면, 이는 모델이 Training data에만 너무 특화되어 일반화 성능이 떨어질 수 있는 overfitting의 신호일 수 있습니다.

Goodfit

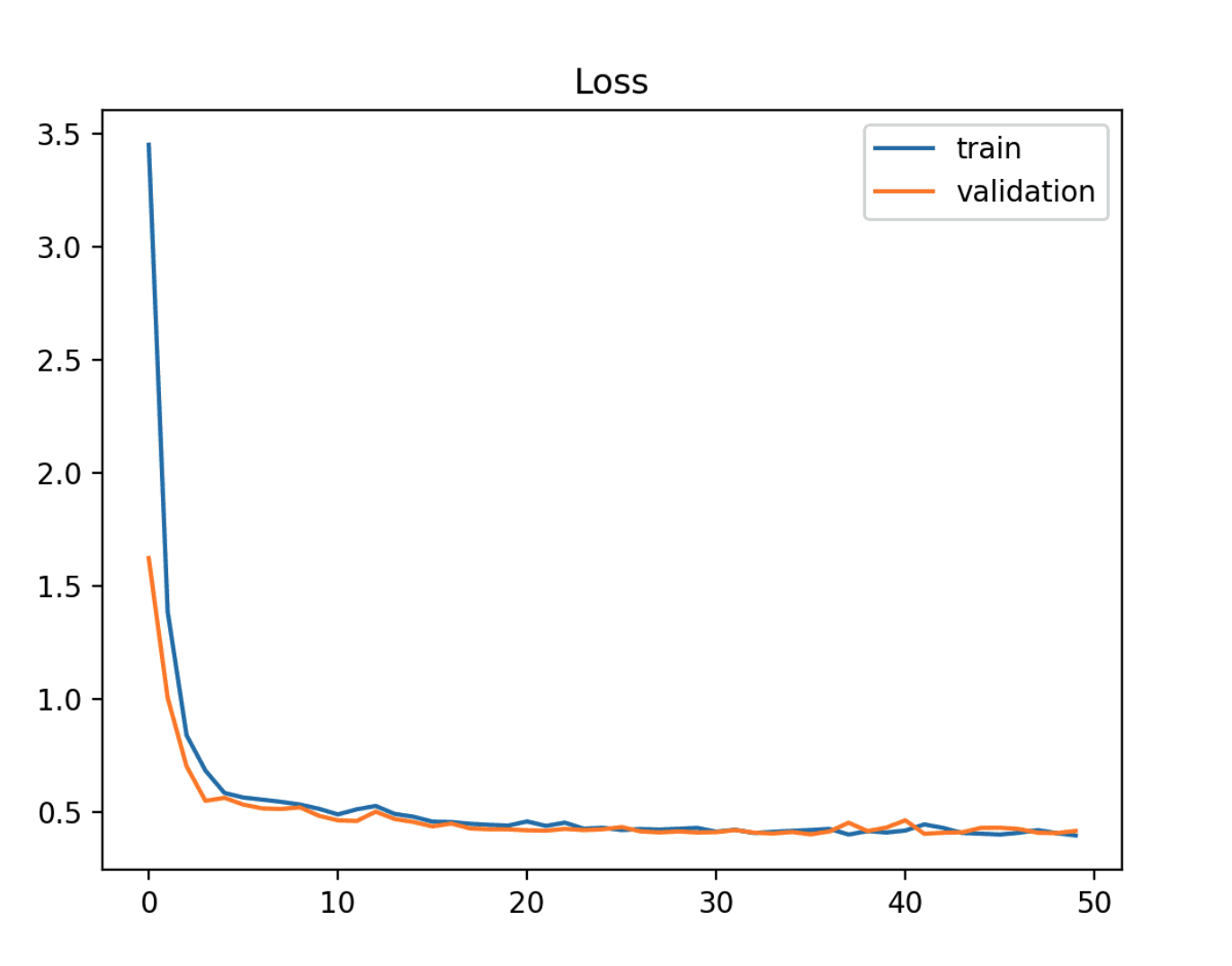
The goal of the learning algorithm and exists between an overfit and underfit model.
A good fit은 training and validation loss가 두 최종 loss 값 사이의 격차가 최소화되면서 안정된 지점까지 감소하는 것을 보여주는 것을 의미합니다.
모델의 loss는 거의 항상 validation dataset보다 training dataset에서 더 낮습니다. 즉, train and validation loss learning curves 사이에는 약간의 Gap은 있어야 한다는 것을 의미합니다.

〽️ Goodfit의 조건

Training loss가 안정된 지점까지 감소합니다.
validation loss가 안정된 지점까지 감소하고 training loss와의 작은 gap이 있는 경우
Continued training of a good fit will likely lead to an overfit.

Cross Validation

Trainset과 Testset을 8:2 비율로 Data를 shuffle해서 나눕니다.
데이터는 k개의 동일한 크기의 subset으로 분할되며, 각각의 subset은 한번씩 validation set으로 사용되고 나머지는 training set으로 사용됩니다.
이 과정은 모든 서브셋이 한 번씩 검증에 사용될 때까지 반복됩니다.
이를 통해 모델의 성능을 보다 정확하게 평가하고, 특정 데이터셋에 과도하게 의존하지 않는 모델을 개발할 수 있습니다.

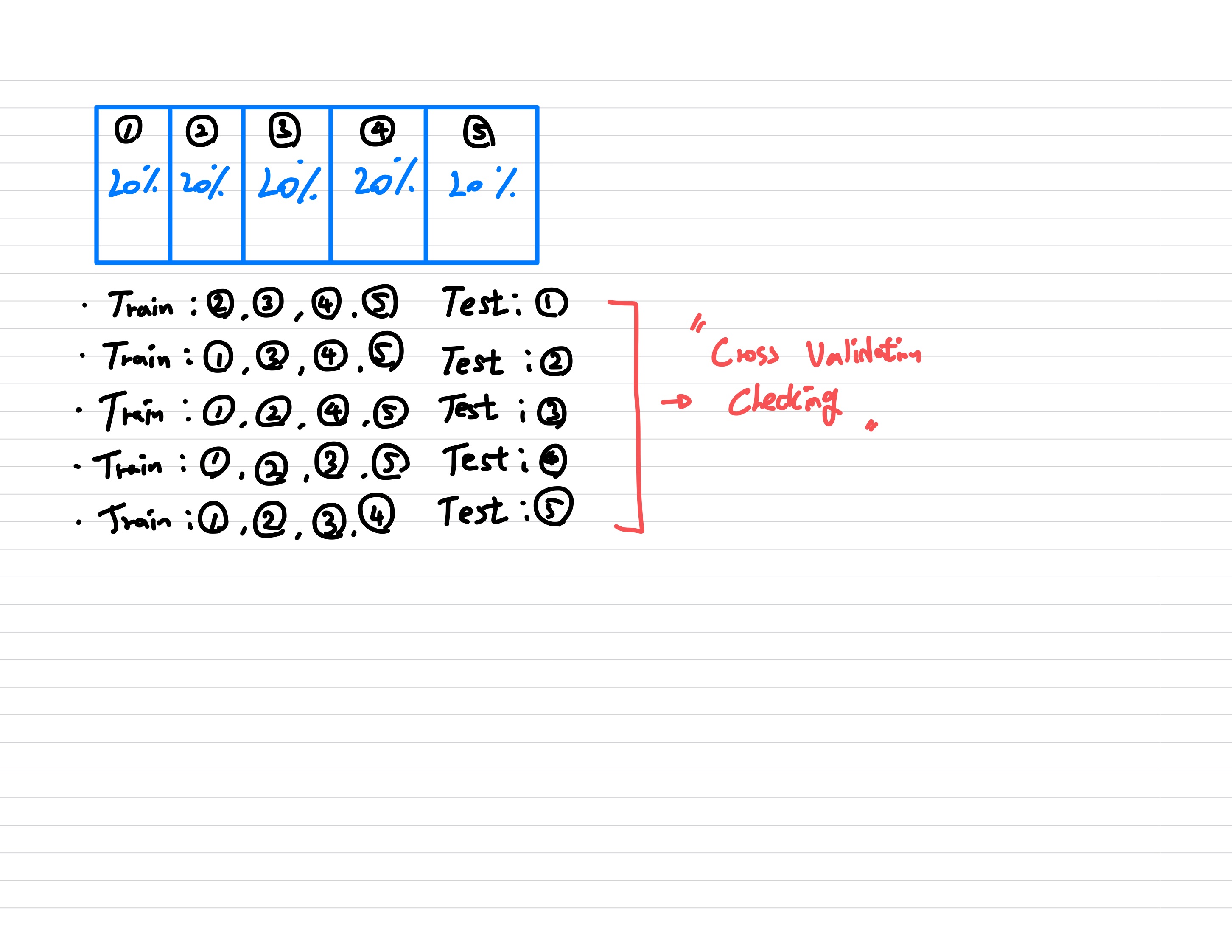
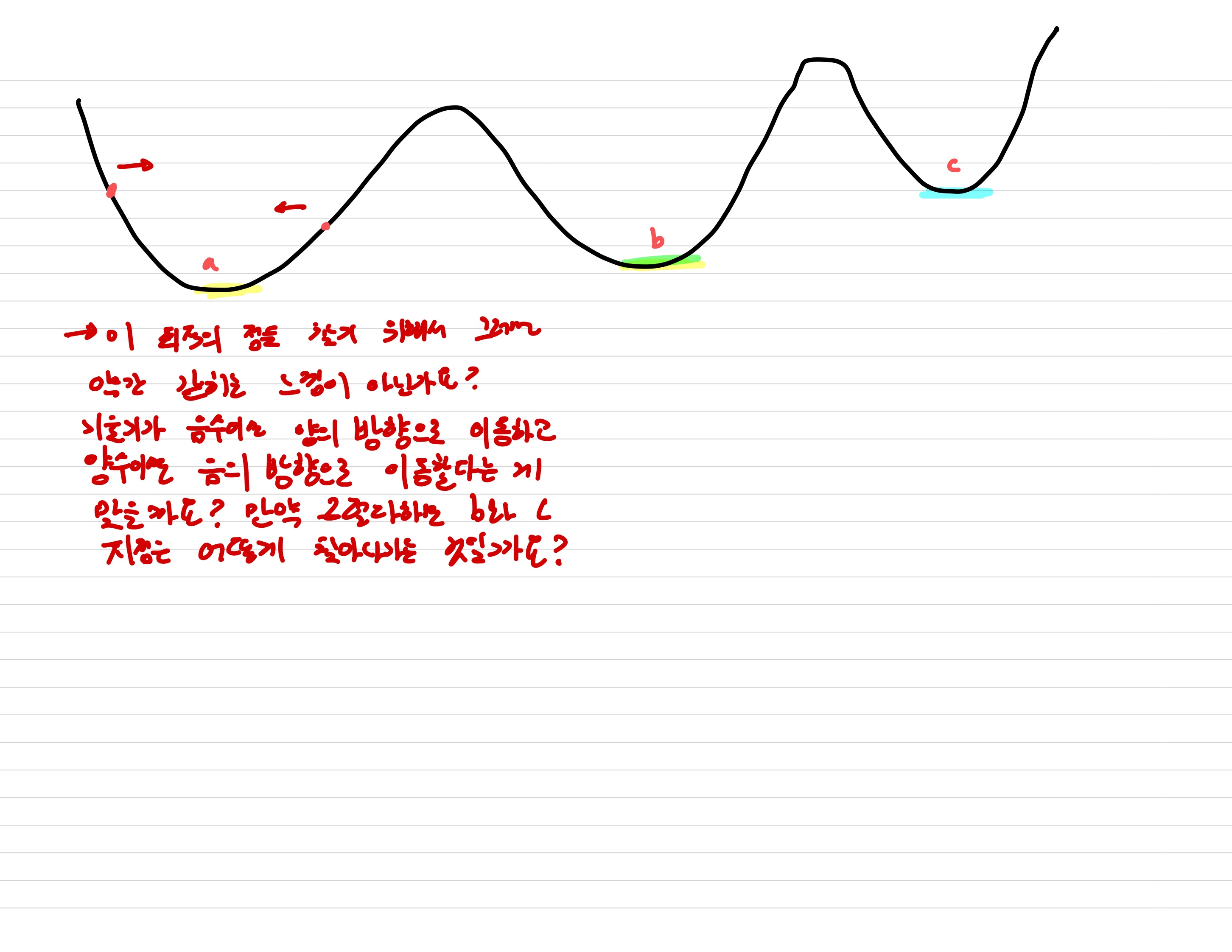
❓ 궁금한 것

일반 Regression 모델에서는 최소의 loss를 찾기 위해 최적의 모델의 파라미터를 찾는 작업을 하는 것인데, 기울기가 음수이면 양의 방향으로 이동하고, 기울기가 양수이면 음의 방향으로 이동하면서 0이되는 지점을 찾는 것으로 알고 있는 데 이렇게 되면 그 안에서 갇히지 않을까요? 또, 그럼 b와 c 지점은 어떻게 찾아나가야 하는 것일까요?