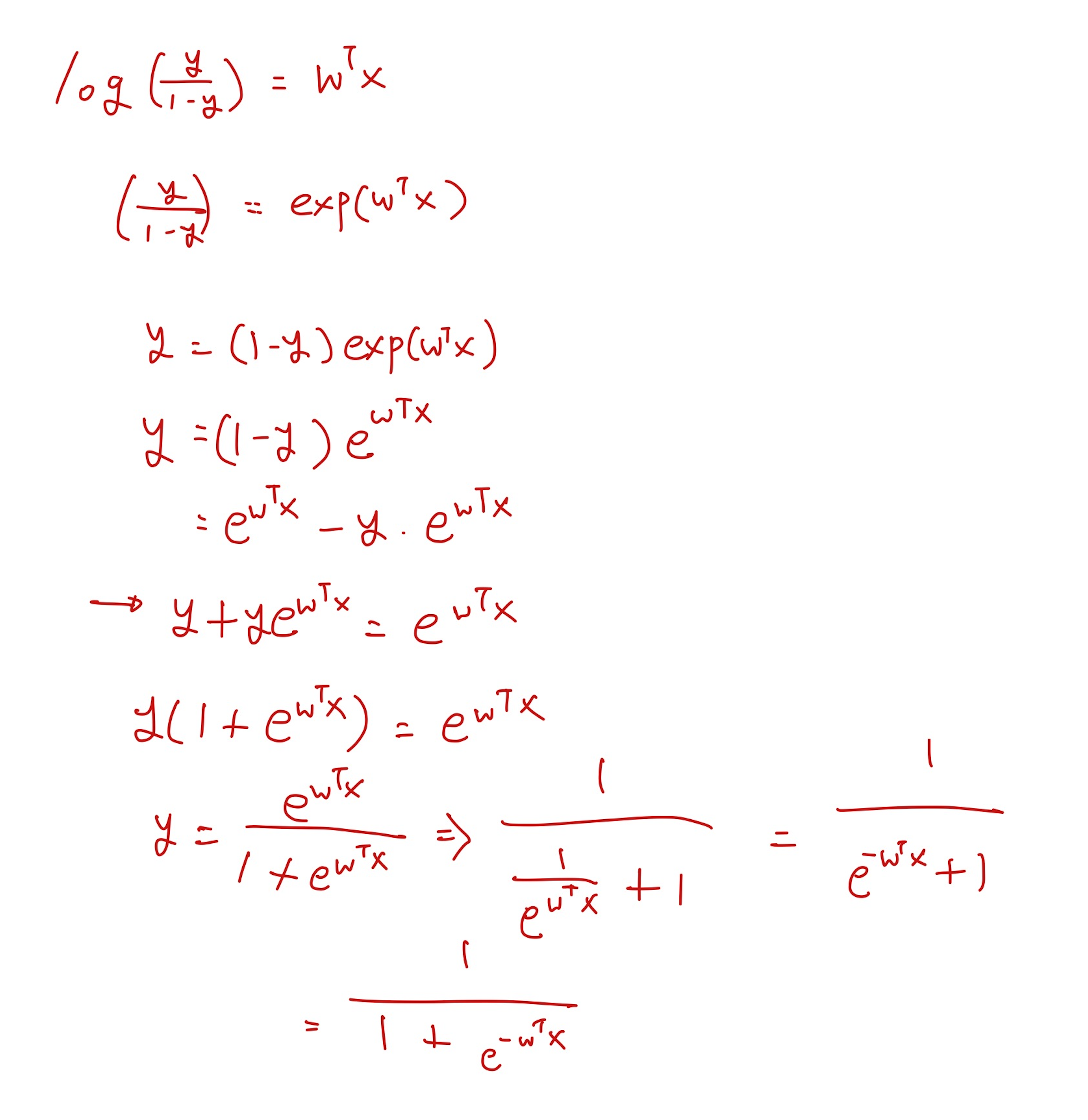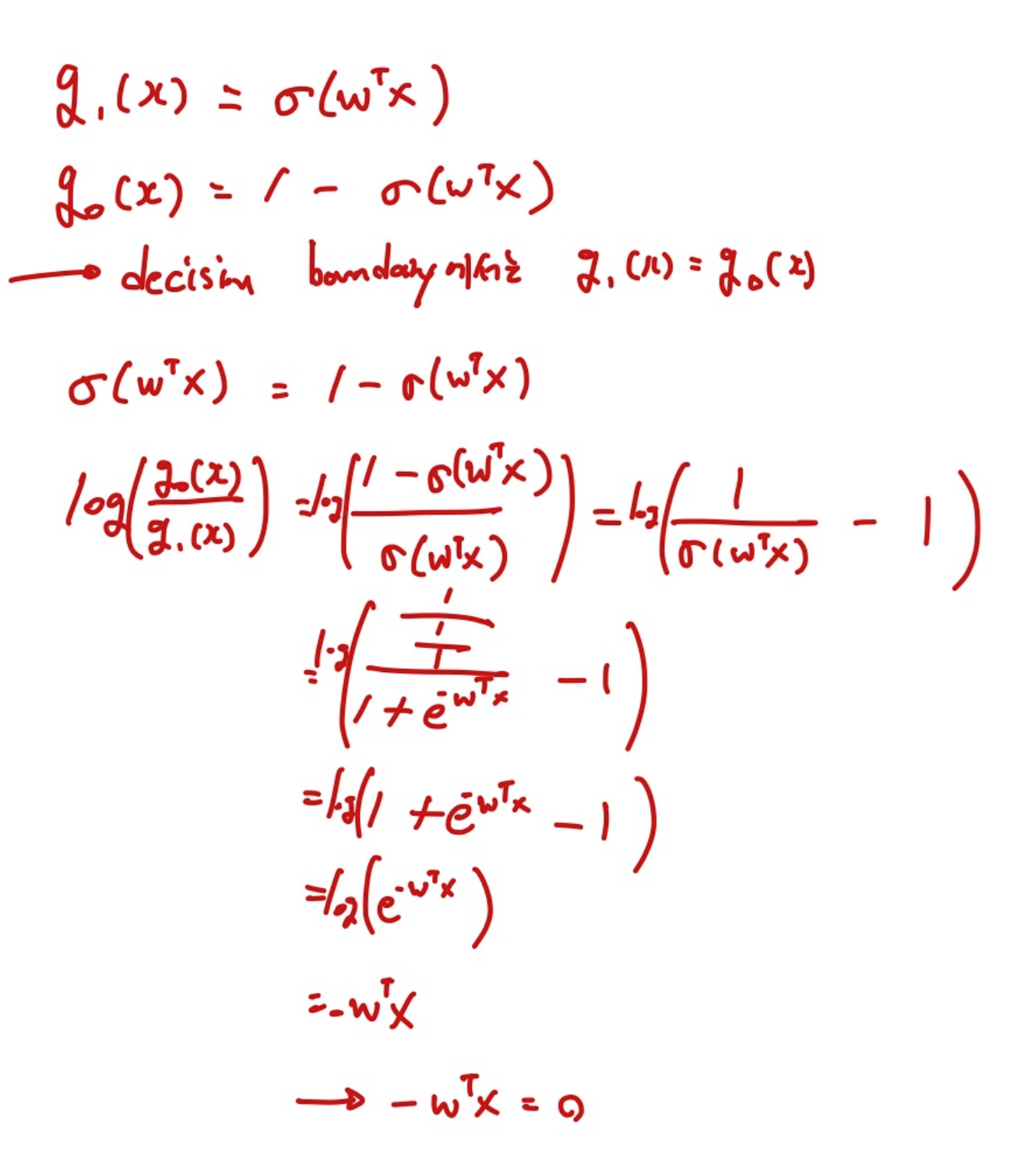Discriminant Functions for Binary Targets
각 클래스(클래스 0과 클래스 1)에 대해 하나씩 두 개의 판별 함수 g0(x)와g1(x)를 가정합니다.
- g0(x)=w0Tx: 클래스 0에 대한 판별 함수
- g1(x)=w1Tx: 클래스 1에 대한 판별 함수
- w0과 w1은 각 클래스에 대한 가중치 벡터입니다.
훈련(Training)
주어진 데이터 포인트 x와 타겟 레이블 y를 사용하여 각 판별 함수의 가중치를 학습합니다.(초기 단계의 분류법)
- y=1인 경우
- g1(x) 판별 함수를 훈련합니다. 이는 데이터 포인트 x가 클래스 1에 속한다고 가정하고, 해당 가중치 w1을 사용하여 x를 어떻게 분류해야 할지를 학습합니다.
- 동시에, g0(x) 판별 함수도 훈련하는데, 여기서는 x가 클래스 0에 속하지 않는다고 가정하여 가중치 w0을 학습합니다.
- y=0인 경우
- g1(x) 판별 함수를 훈련하는데, 이번에는 x가 클래스 1에 속하지 않는다고 가정합니다. 이 경우에는 y=1일 때와 반대로 가중치 w1을 학습합니다.
- g0(x) 판별 함수는 x가 클래스 0에 속한다고 가정하고 가중치 w0을 학습합니다.
- 예를 들어, y=1일 때, g1(x)=w1Tx로 모델을 훈련시키고, y=0일 때는 g1(x)를 −w1Tx와 같이 훈련시킴으로써, 모델이 양의 클래스 레이블을 가진 데이터와 음의 클래스 레이블을 가진 데이터를 구분할 수 있도록 합니다.
- 빨간색 데이터를 1, 파란색 데이터를 0으로 레이블을 했다고 가정한다. g1(x) 가 1에 가까워지면 빨간색 데이터, 0에 가까워지면 파란색 데이터가 된다. 반대로, 빨간색 데이터를 0, 파란색 데이터를 1로 레이블을 했다고 가정한다. 그러면 g0(x) 가 1에 가까워지면 파란색 데이터, 0에 가까워지면 빨간색 데이터가 된다.
- g0(x)와 g1(x)의 대소 관계를 비교해서 파란색인지 빨간색인지를 구별한다.
- Least Squares Error를 사용하여 g0(x)과 g1(x)를 찾는다.
개선된 방법
-
데이터 포인트 x가 클래스 1에 속하는 경우, 즉 타겟 레이블 y가 1인 경우, g1(x)를 wTx로 훈련합니다.
-
데이터 포인트 x가 클래스 0에 속하는 경우, 즉 타겟 레이블 y가 -1인 경우, g1(x)를 −wTx로 훈련합니다.
-
분류
- g1(x)=wTx>0→ class 1
- g1(x)=−wTx<0→ class 0
- g1(x)=wTx=0→ 의사 결정을 하는 boundary 지점
- 1에 가까울 수록 1번 클래스, -1에 가까울 수록 0번 클래스
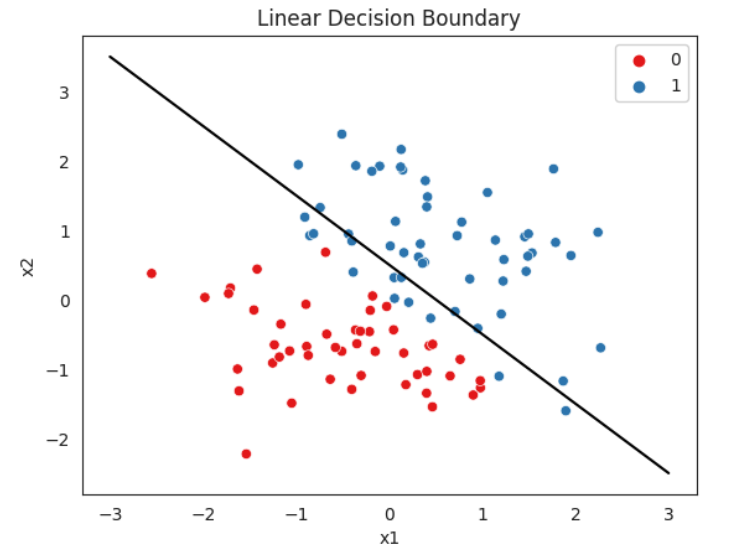
- 파란색 부분은 g1(x)>0, 빨간색 부분은 g1(x)<0, 경계선은 wTx=0, g0(x)=g1(x)
한계
- Regression은 Gaussian distribution과 관련이 있습니다. Regression에서 우리가 추정하는 것은 조건부 확률 분포 P(y∣x;w)이며, 이는 입력 x와 가중치 w에 대한 선형 조합으로 y의 조건부 가우시안 분포를 의미합니다. Regression은 연속적인 값을 예측할 때 유용하지만, Binary Target과 같은 이산적인 값을 예측하기 위해서는 이 방법의 한계가 있습니다.
- Regression의 예측은 제한되지 않은 값이 될 수 있습니다. 즉, 0과 1의 범위를 벗어난 값을 예측할 수 있습니다. 확률은 0과 1사이의 값이어야 하는데, Regression으로는 이 조건을 항상 만족시키지 못합니다.
- Binary Target의 경우, 실제 데이터 분포는 이러한 가정을 따르지 않을 수 있습니다.
- 이러한 한계를 극복하기 위해, 확률적 모델을 사용해서, P(y=1∣x)또는P(y=0∣x)를 추정하고 싶을 수 있습니다.이러한 확률적 접근 방식은 분류 문제에서 더 자연스럽습니다. 왜냐하면 우리는 가능한 결과가 연속적인 값의 범위가 아니라 특정한 이산적인 클래스 중 하나임을 알고 있기 때문입니다. 그래서 이러한 확률적 모델을 사용하면, 예측에 대한 불확실성을 수치로 표현할 수 있고, 여러가지 의사결정 기준을 적용할 수 있습니다.
Logistic Regression
Logistic function를 사용하여 discriminate function을 이끄는 법
- g1(x)=σ(wTx), g0(x)=1−σ(wTx), σ(z)=1+e−z1로 정의된 logistic function이며, 출력이 0과 1사이로 제한되도록 합니다.
- sigmoid와 같은 activation function을 사용하는 궁극적인 목적은 unlinearlity(비선형성)을 표현하기 위함입니다.
- Logistic Regression은 출력을 확률로 해석할 수 있기 때문에, 결과가 Binary인 경우에 대한 예측에 있어서 더 정확한 정보를 제공할 수 있습니다.
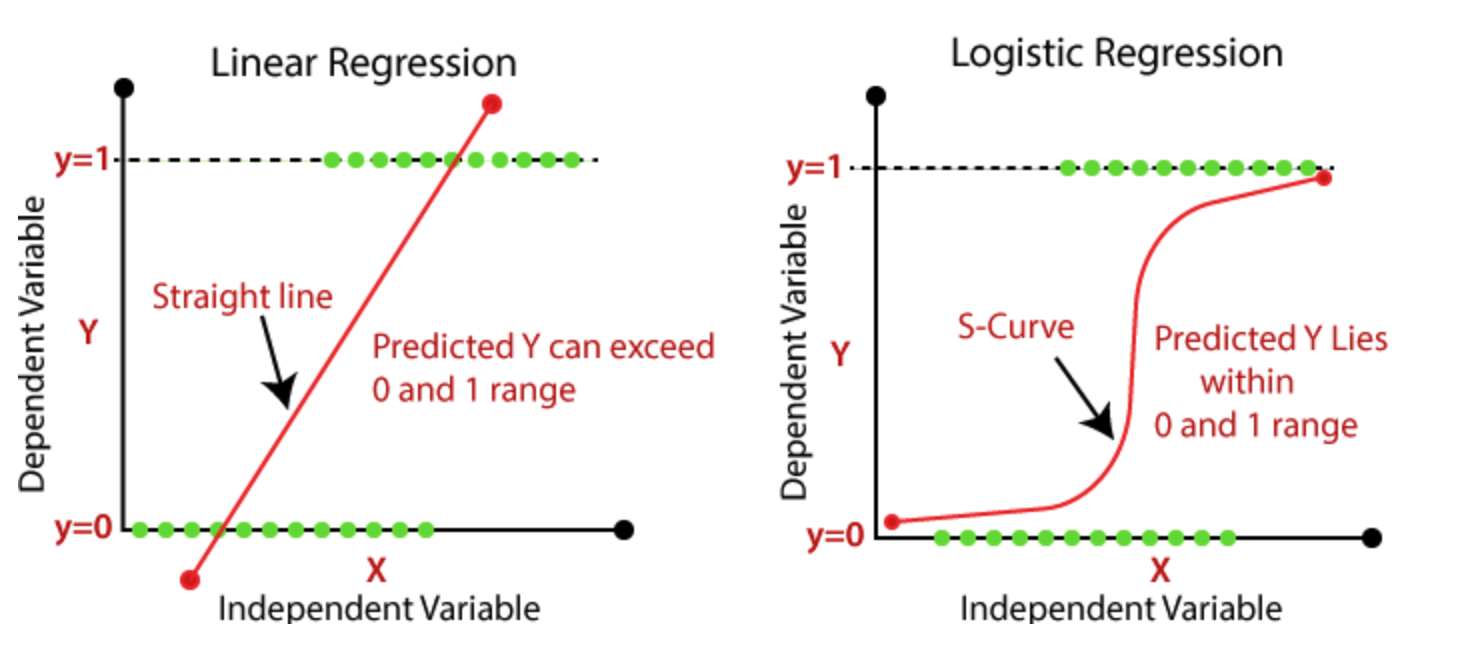
- Linear Regression과는 달리 Logistic Regression은 S자 형태의 Logistic Function을 사용하여, 더 복잡한 패턴을 가진 데이터에 대해서도 효과적인 Decision Boundary를 형성할 수 있습니다.
- 0과 1사이의 수가 나오고, 0보다 작거나, 1보다 큰 수가 나오지 않는다는 점이 장점입니다.
- 의사결정을 0과 1에 가깝게 하고, 중간지점이 매우 smooth하게 연결되어있습니다.
Smooth Switching Function
- Smooth Tranisition : sigmoid 함수는 입력 값이 변함에 따라 출력값이 0과 1사이를 부드럽게 전환합니다. Linear Regression과는 달리 갑작스러운 변화가 아닌 점진적인 변화를 의미합니다.
- S자 형태 : Sigmoid 함수의 S자 형태는 중간 지점 근처에서 가장 민감하게 반응합니다. 입력 값이 증가하면 출력 값이 0에서 1로 천천히 증가하다가 중간지점(임계값)에서 빠르게 증가하기 시작하고, 그 후 다시 천천히 증가하여 1에 도달합니다.
Probability Estimation
- g1(x)=σ(wTx)=P(y=1∣x)
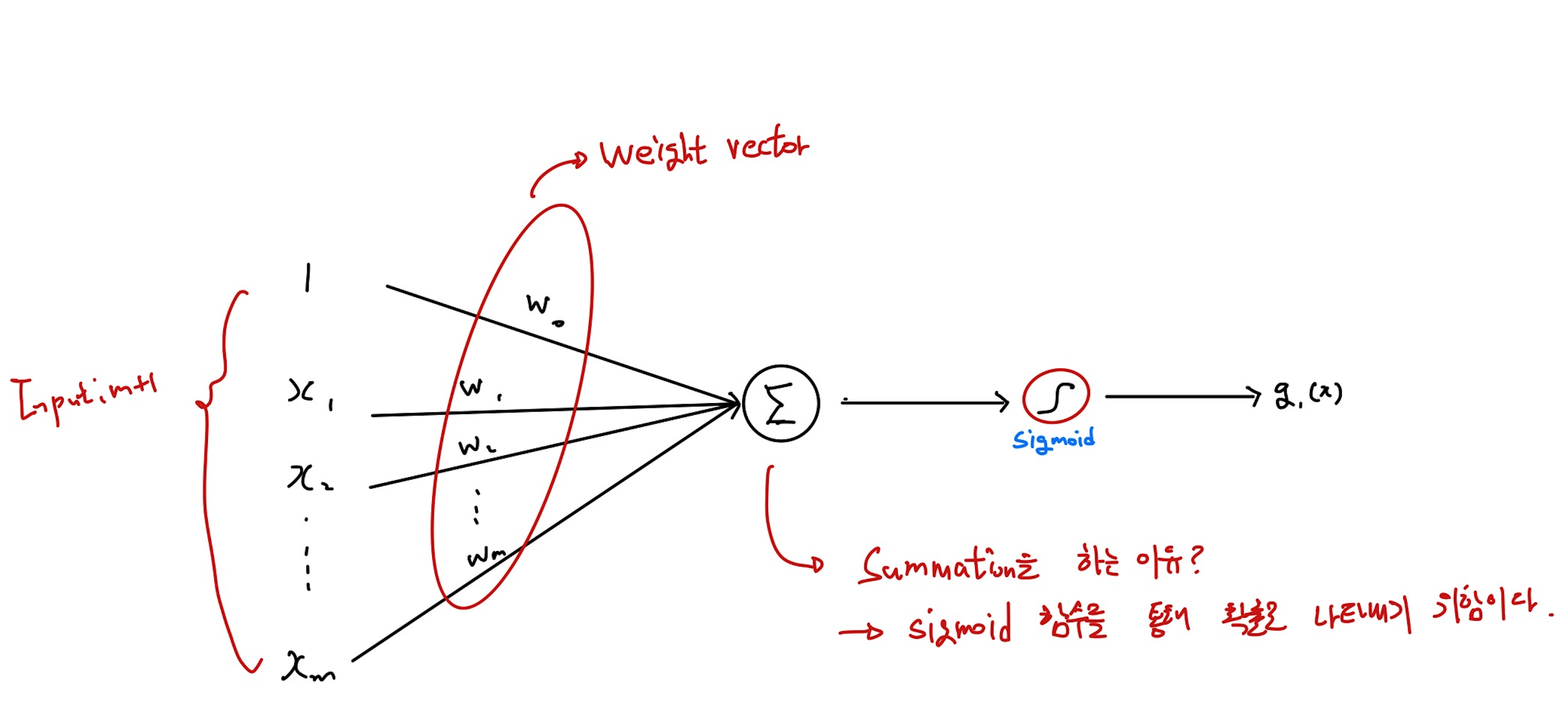
- Summation을 해서 sigmoid function을 통해 확률적으로 나타낸다는 것이 잘 이해되지 않아 실제 값을 넣고 예시를 적용해보았습니다.
- Input x = [1, 3, 2], 가중치 벡터 w = [0.8, -0.5, 0.2]라고 할때, wTx=−0.3, 이에 sigmoid 함수를 적용하면 약 0.426이 됩니다.
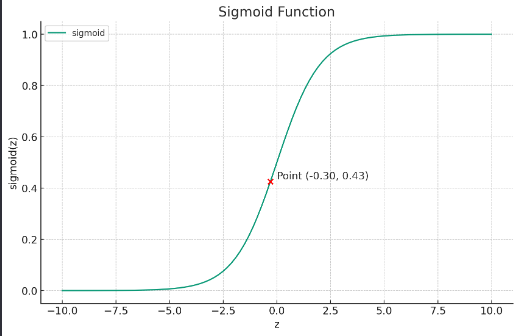
- z 축에서 -0.3 위치에 있고, σ(z) 축에서는 약 0.426의 값을 가집니다. 이는 해당 데이터 포인트가 클래스 1에 속할 확률을 약 42.6%로 예측하는 것을 의미합니다.
- 결론은 sigmoid function을 통해 확률적으로 나타냄을 위한 것입니다. 이로써 나의 데이터 포인트가 어떤 클래스에 위치하는 지에 대한 값을 예측 가능합니다.
- y=1+e−z1=1+e−wTx1
- odds = 1−yy, 여기서 y는 클래스 1에 속할 확률을 나타내고, 1-y는 클래스 0에 속할 확률입니다.
- odds는 특정 이벤트가 발생할 확률과 그 이벤트가 발생하지 않을 확률의 비율을 나타냅니다.
- logit(y)=log(1−yy), y의 값(클래스 1에 속할 확률)과 1-y(클래스 0에 속할 확률)의 비율인 odds에 자연로그를 취한 것입니다.
- log(1−yy)=wTx
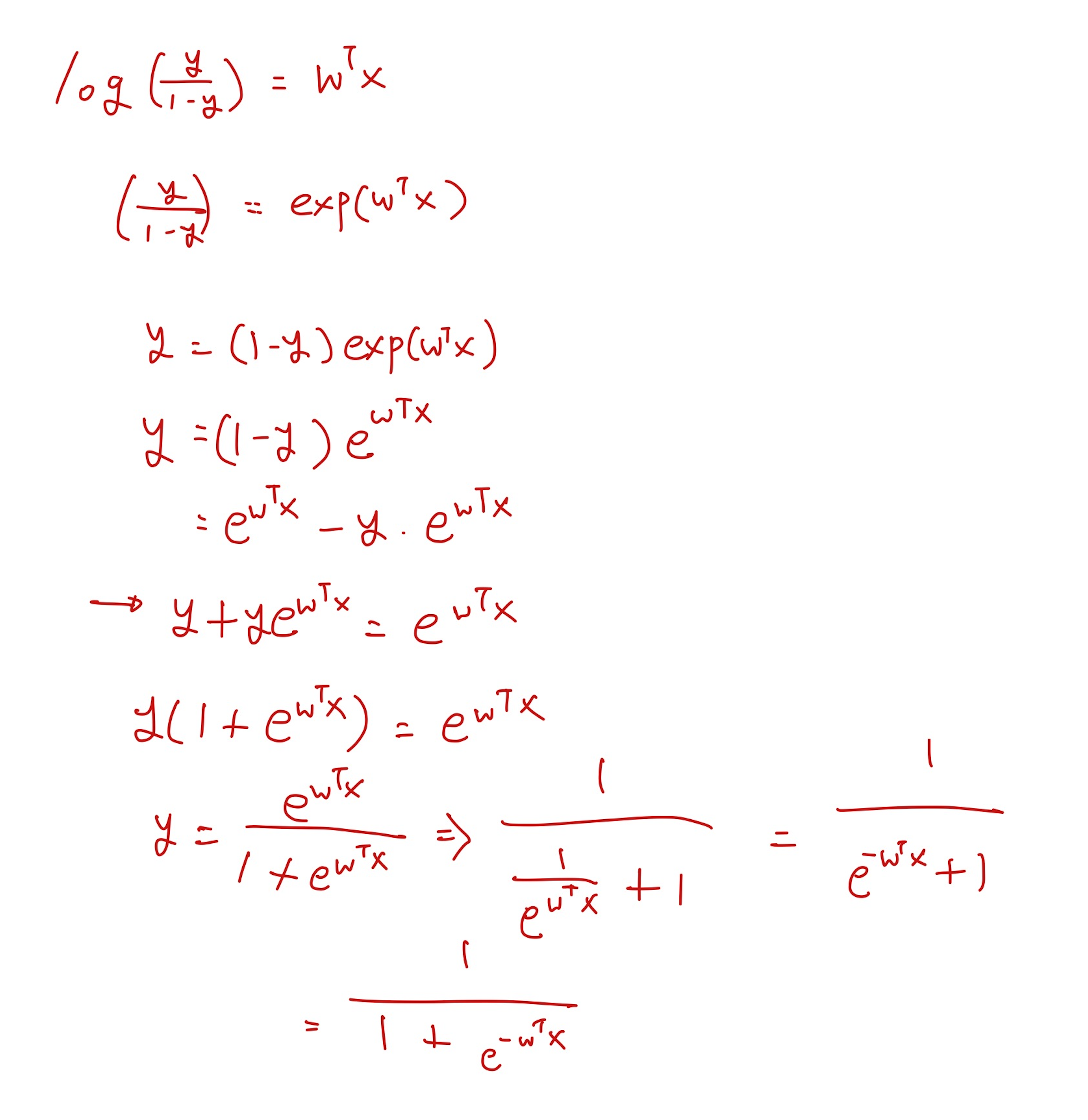
- y=σ(wTx)=1+e−wTx1
- Probablistic function f:X→[0,1], where f descriobes P(y=1∣x)
즉, x가 주어졌을 때 class 1에 속할 확률을 나타내는 것입니다.
- f(x;w)=σ(wTx)=P(y=1∣x;w)
- P(y=0∣x;w)=1−P(y=1∣x;w)
- P(y=1∣x;w)≥21이면, class 1에 속한다고 생각하고, 그렇지 않으면 class 0에 속한다고 생각할 수 있다.
LogReg의 Decision Boundary 찾기
Boundary Decision은 두 클래스 간의 경계에서, 두 판별 함수 g1(x)와 g0(x)가 동일한 값을 가집니다.
g1(x)=σ(wTx), g0(x)=1−σ(wTx)로 정의합니다.
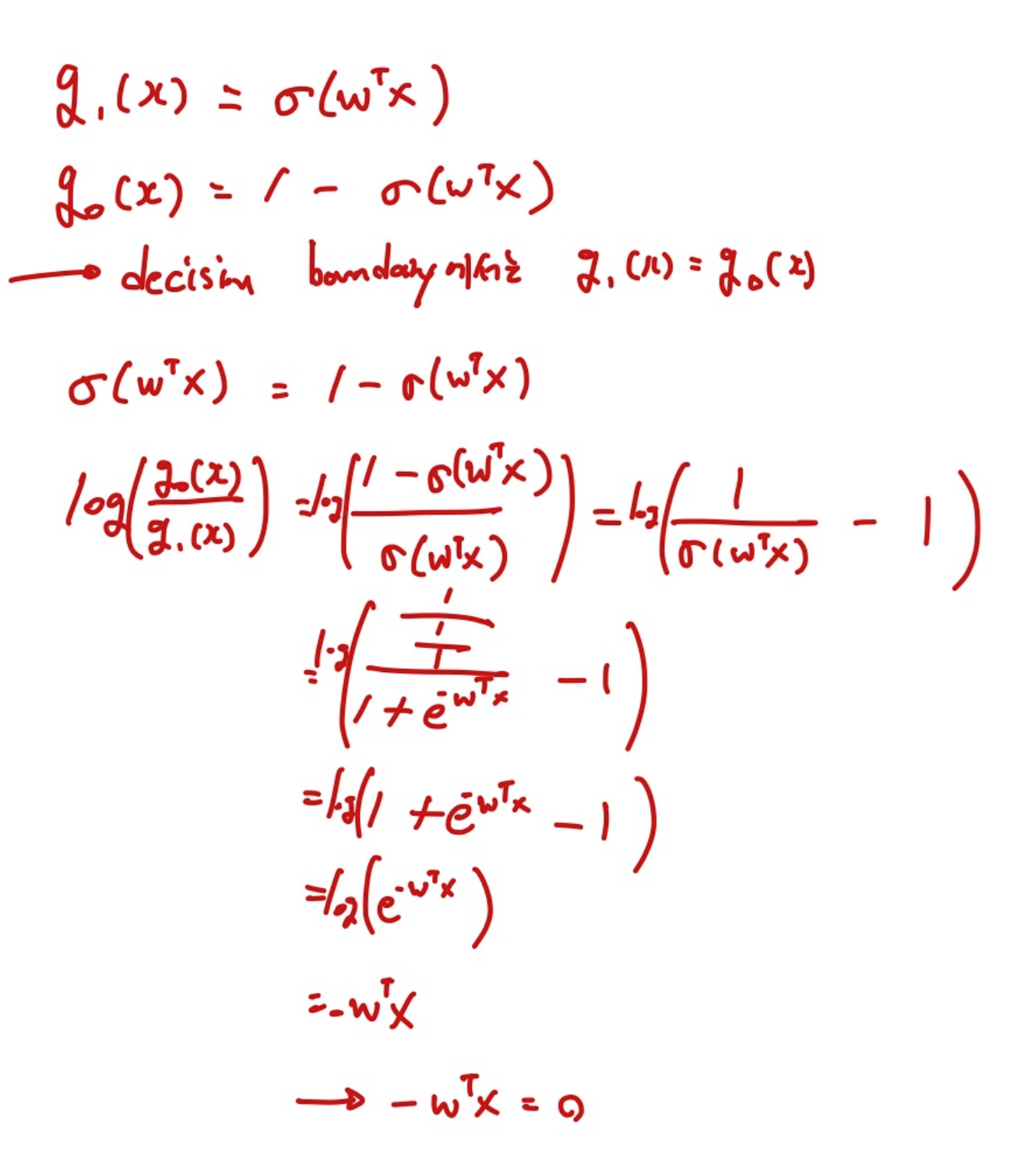
- 여기서, sigmoid function의 출력이 0.5인 지점은 z가 0일 때입니다. 여기서 z는 wTx이고, 따라서 wTx=0을 의미합니다. 데이터 포인트가 클래스 1에 속할 확률과 클래스 0에 속할 확률이 정확히 동일합니다.
Training
-
dn=(xn,yn), un=P(yn=1∣xn;w)=σ(zn)=σ(wTxn)
- P(yn=0∣xn;w)=1−un=1−σ(zn)
-
L(d;w)=∏n=1NP(yn∣xn;w)=∏n=1N(un)yn(1−un)1−yn
- 이 곱은 각 데이터 포인트에서 관찰된 레이블이 모델에 의해 예측된 확률에 따라 발생할 확률입니다. 이는 베르누이 분포를 따릅니다.
- Likelihood를 직접 최적화하는 것은 계산상의 문제(numerical underflow)로 인해 어려울 수 있으므로, log-likelihood를 사용합니다. 로그를 취함으로써 곱셈이 덧셈으로 변환되어 계산기 간단해지고, 최적화 과정이 수치적으로 안정화됩니다.
-
xn→σ(wTx)=u
-
xn→σ(wTxn)=un
-
ℓ(d;w)=logL(d;w)=log∏n=1NP(yn∣xn;w)
=log∏n=1N(un)yn(1−un)1−yn
=∑n=1Nyn(logun)+(1−yn)log(1−un)
- log-likelihood를 최대화하는 가중치 w를 찾는 것입니다.
-
log-likelihood 미분 :
- ∂wj∂ℓ(d;w)=∑n=1Nxn(yn−σ(wTxn))
- 미분값이 0을 만드는 최적의 w를 찾아야 합니다.
-
Gradient Ascent : 주어진 데이터셋에 대한 모델의 매개변수를 최적화하여 log-likelihood의 최대값을 찾는 데 사용됩니다.
- wt=wt−1+α∇wℓ(d;w)∣wt−1
-
Cost function
- Cost J(w,d)=−N1ℓ(d;w)
= −N1∑n=1N[ynlogun+(1−yn)log(1−un)]
-
Gradient Descent with J(w,d)
- wt=wt−1−α∇wJ(d;w)∣wt−1
= wt=wt−1−α∇w(−N1ℓ(d;w))wt−1
= wt←wt−1−α(−N1∑n=1Nxn(yn−σ(wTx)))wt−1
-
Online Learning Algorithm(SGD)
- Jonline(w,d(n))=−[y(n)log(μ(n))+(1−y(n))log(1−μ(n))]
- 한 번에 하나의 데이터 포인트 또는 작은 배치를 사용하여 매개변수를 업데이트합니다.
- SGD에서는 각 업데이트에서 단일 데이터 포인트에 대한 손실만 고려하므로, 평균을 취할 필요가 없습니다.
- 대신, 각 스텝에서 즉시 매개변수를 업데이트하여 더 빠르게 학습하고, 더 빠른 반복을 통해 최적화합니다.
- wt←wt−1−α(yn−f(xn,wn−1))xn
-
Regularization
-
Ridge(L2) → make unnecessary w close to zero. not zero.
- J(w,D)=−logP(D∣w)+λ∥w∥22
= −[∑n=1Ny(n)log(σ(wTx(n)))+(1−y(n))log(1−σ(wTx(n)))]+λ∥w∥22]
- 가중치의 크기를 제한하여 각 특성의 영향력을 줄이는 효과가 있습니다.
-
Lasso(L1)
- J(w,D)=−logP(D∣w)+λ∥w∥1
= −[∑n=1Ny(n)log(σ(wTx(n)))+(1−y(n))log(1−σ(wTx(n)))]+λ∥w∥1]
- 가중치 중 일부를 정확히 0으로 만들어 해당 특성을 모델에서 제외시키는 효과가 있으며, 이를 통해 feature selection이 자연스럽게 이루어집니다.
-
Elastic Net(L1 + L2)
-J(w,D)=−logP(D∣w)+λ1∥w∥1+λ2∥w∥22
- Lidge와 Lasso의 접근 방법을 결합한 Regularization 기법입니다. Elastic Net은 loss function에 가중치 벡터의 L1-norm과 L2-norm을 동시에 더하여, 두 정규화 기법의 장점을 모두 취합니다.
✅ 헷갈렸던 부분
∑n=1Ny(n)log(σ(wTx(n)))+(1−y(n))log(1−σ(wTx(n)))
- 여기에서 wT와 xn을 연산하는 게 이해가 되지 않았다. 왜냐하면, xn은 데이터 포인트 중 하나이기 때문이다. 다시 생각해보니 데이터 포인트 안에는 3차원 특성이 있다고 가장하면 w vector 역시 3차원으로 나올 것이다.
- w=[w1,w2,w3]
- xn=[x1n,x2n,x3n]
- wTxn=w1x1n+w2x2n+w3x3n
- 결국 데이터 포인트의 각 feature들을 담고 있는 것이 xn이었고, 그 feature 별로 각 w를 학습시켜 나가는 과정이다. 이것을 잊지말자.!
왜 λ의 값이 크면 클수록 모든 가중치가 더 작아지는 것인가?
-
가중치 값이 비교적 작은 값의 값이 더욱 줄어들게 됩니다.
-
∇wJ(w)=∇wLoss(w)+2λw
-
w:=w−α∇wJ(w)
-
w:=w−α(∇wLoss(w)+2λw)
-
λ값이 클수록, 가중치 업데이트 과정에서 가중치 w에 부과되는 패널티가 커지고, 이는 각 반복에서 가중치 w를 더 크게 감소시킵니다. 결과적으로, 모델은 더 작은 가중치 값을 가지게 되어 복잡성이 감소하며, 이는 overfitting을 방지하는 데 도움이 됩니다.
-
단순히 말해서, λ 값이 크면 비용 함수의 정규화 항이 모델의 총 비용에 더 크게 기여하게 되므로, 가중치의 크기를 줄이는 것이 전체 비용을 줄이는 데 더 중요해집니다. 가중치가 줄어드는 것은 모델이 데이터의 노이즈에 덜 민감하게 되어, 모델이 더 일반적인 패턴을 학습하도록 유도합니다.
참고자료
https://iq.opengenus.org/decision-boundary/
https://www.javatpoint.com/linear-regression-vs-logistic-regression-in-machine-learning