[ML] Linear Discriminant Analysis(LDA)

Linear Discriminant Analysis(LDA)

Classification

X is discrete or continuous $\to$ Y is discrete.

Discriminant functions

• 패턴 인식과 머신러닝에서 사용되는 개념으로, 주어진 데이터를 다른 클래스나 범주로 구분하는 데 사용됩니다.(Supervised Learning)

• 입력 데이터가 주어졌을 때, 이 데이터가 어떤 클래스에 속하는 지 결정합니다. 이는 데이터의 특성을 기반으로 한 Decision Boundary를 만들어냅니다.(input $x \space$, choose class c with the higheset $g_c(x)$)

• $y^*=argmax\space g_c(x)$, $g_c(x)$는 data instance가 class c에 속한다고 판단되면 output을 최대화합니다. $\rarr$ Decision making with a discriminant function.

• LinReg : Discriminative $P(y|x) ... P(y|x;w)$ Parameter w가 이 확률 분포에 어떻게 영향을 미치는지를 구분하는 데 사용합니다. 해석해보자면, 주어진 입력 x와 파라미터 w에 대해 y가 나타날 확률을 의미합니다.

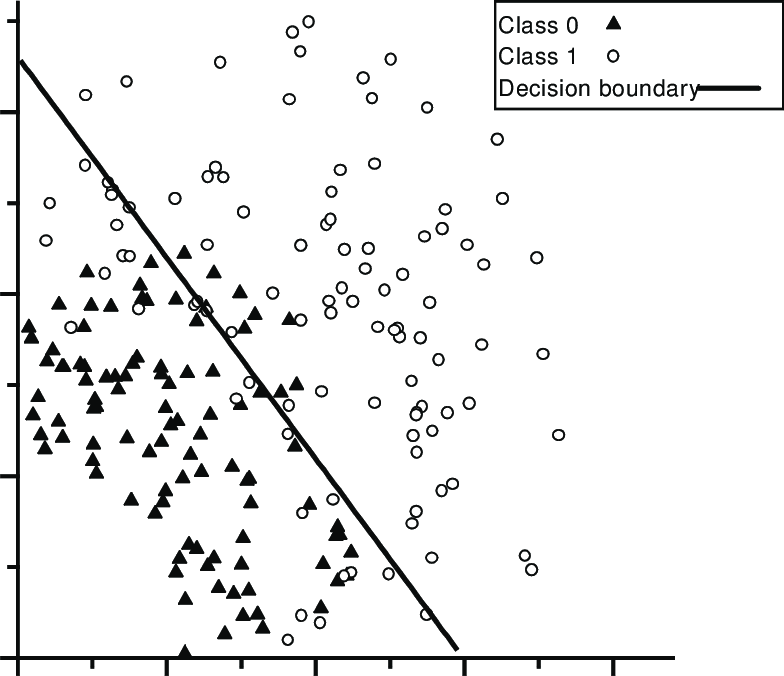
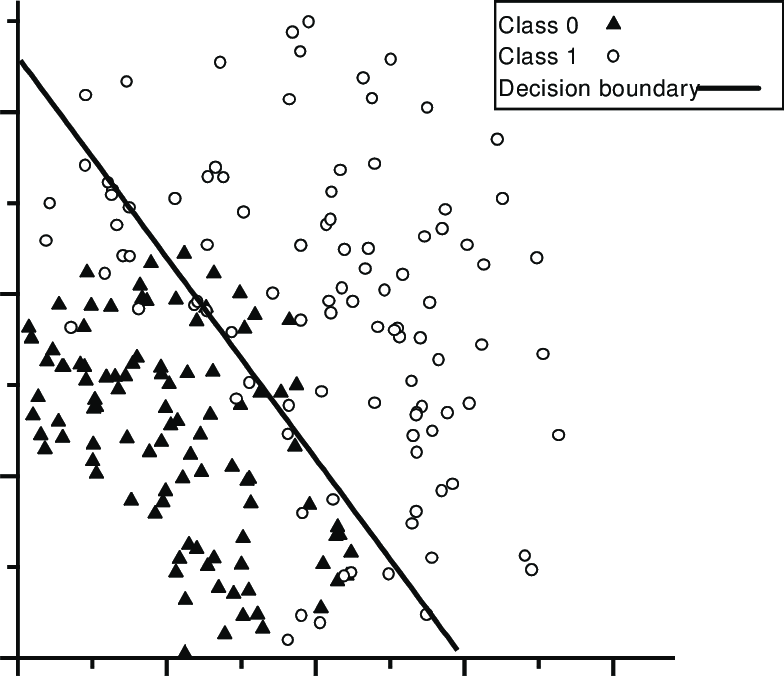
• $g_1(x) > g_0(x) \rarr$ class1이 많이 몰려있는 곳
• $g_1(x) < g_0(x) \rarr$ class0이 많이 몰려있는 곳
• $g_1(x) = g_0(x) \rarr$ 경계선을 의미합니다. 즉, Decision boundary!

Genearative Classifier

• 주어진 데이터의 확률적 속성을 학습하고, 이 정보를 사용하여 새로운 데이터 샘플이 어떤 클래스에 속할 확률을 추정합니다.

• $P(y=c|x; \theta) = \frac{P(x|y=c;\theta)p(y=c;\theta)}{\sum_{c'}P(x|y=c';\theta)P(y=c';\theta)}$

  • $P(x|y=c; \theta)$ : class c가 주어졌을 때, 특정 데이터 포인트 x가 나타날 확률을 의미합니다. 즉, Class c 내의 데이터 분포를 나타냅니다.
  • $P(y = c; \theta)$ : 이는 모델이 주어진 매개변수 $\theta$를 바탕으로 특정 클래스의 데이터가 관찰될 확률을 추정하는 것입니다.

• 데이터가 어떻게 생성되는 지에 대한 모델을 구축하고, 각 클래스에 대한 데이터의 분포를 학습하는 것을 포함합니다.

Linear Discriminant Analysis

Goal : 클래스 간의 분리를 최대화(Between-class separability)하는 동시에 클래스 내의 분산을 최소화(with-class variability)를 최소화하는 선형 조합을 찾는 것입니다.

• 서로 다른 데이터 클래스를 최소한의 오류로 구분할 수 있는 라인에 D-dimensional data를 Projecting하는 문제를 고려합니다.

• discrimination을 효율적으로 하는 projection을 찾아야 합니다.

• 새로운 저차원 공간으로의 투영 : 계산된 축(또는 벡터)를 사용하여 데이터를 저차원 공간으로 투영합니다. 이 저차원 공간에서는 클래스 간 분리가 최대화됩니다.

  • 축(벡터)의 계산 : 먼저, LDA는 데이터를 가장 잘 구분하는 축을 찾습니다. 이 축은 클래스 간 분산을 최대화하고 클래스 내 분산을 최소화하는 방향(축)입니다.
  • 데이터의 변환 : 이 축들을 기반으로, 원래 고차원의 데이터 포인트를 새로운 저차원 공간으로 투영합니다. 예를 들어, 100차원의 데이터를 2차원으로 줄이려면, 가장 정보가 많은 두 개의 축을 찾아 이 축들에 대해 데이터를 투영합니다.
  • 저차원 공간에서의 표현 : 투영된 데이터는 이제 저차원 공간에 있으며, 이 공간에서 데이터 포인트들은 원래 고차원 데이터의 중요한 특징을 반영하면서도 차원이 줄어든 형태로 표현됩니다.

• Fisher's criterion

  • 각 class 평균의 분산은 최대화 하고, 클래스 내의 분산은 최소화해야한다!!

Training

• Maximize $\frac{between-class \space separability}{within-class \space variability}$ (binary classification의 가정하)

  $Maximize \space J(w) = \frac{||\hat{m_0} - \hat{m_1}||^2}{\hat{s_0^2} + \hat{s_1^2}}, where \space \hat{m_c} \space and \space \hat{s_c^2}$ 각각 sample mean과 sample variance after projection with w.
  $\hat{m_0} = \mathbf{w^T}m_0$
  $\hat{s_0^2} = w^TS_0^2w$
  $Maximize \space J(w) = \frac{||\hat{m_0} - \hat{m_1}||^2}{\hat{s_0^2} + \hat{s_1^2}}$ $=\frac{w^TS_Bw}{w^TS_Ww}$

  • $||\hat{m_0} - \hat{m_1}|| = (\hat{m_0} - \hat{m_1})(\hat{m_0} - \hat{m_1})^T$

    $= (w^Tm_0 - w^Tm_1)(w^Tm_0 - w^Tm_1)^T$
    $= w^T(m_0 - m_1)(m_0 - m_1)^Tw$
    $=w^TS_Bw$

  • $\hat{s_0} + \hat{s_1} = w^Ts_0^2w + w^Ts_1^2w = w^T(s_0^2 + s_1^2)w = w^TS_Ww$

  • LDA에서는 벡터 w를 사용하여 데이터를 저차원 공간으로 투영합니다. 이 문제는 generalized eigenvalue problem으로 표현됩니다.

  • $w^TS_Bw$를 최대화하고, $w^TS_Ww = 1$인 조건을 만족시키는 w를 찾는 것으로 재정의됩니다.

  • $L(w,\lambda) = w^TS_Bw + \lambda(w^TS_ww -1)$

  • $w^TS_Ww = 1$로 설정하는 이유는 최적화 문제에서 크기 제한을 두기 위함입니다.

    • 크기의 무한성 제한 : 벡터 w의 크기에 제한을 두지 않으면, w의 길이를 무한히 크게 만들어 $w^TS_Bw$ 값을 인위적으로 증가시킬 수 있습니다. 즉, w의 스케일이 최적화 문제의 해결에 영향을 줄 수 있으므로, 이를 표준화하기 위해서 제약 조건을 추가합니다.
    • 일관된 해의 표준화 : w의 길이가 1이 되도록 하는 것은 w를 단위 길이로 표준화하는 것과 동일합니다. 이를 통해 모든 가능한 해들이 동일한 스케일에 있게 되어, 최적화 과정에서 공정한 비교가 가능해집니다.

  • $-\frac{1}{2}w^TS_Bw$를 최소화하고, $\frac{1}{2}w^TS_Ww = \frac{1}{2}$ 여기서 $\frac{1}{2}$을 곱해준 이유는, w가 제곱이 되기 때문에 미분하면 cancel out되게 하기 위해서 곱해주는 것이다. 또한, 최적화 문제에서 상수 배수는 최적화의 해에 영향을 주지 않으므로, 상관없습니다.

  • 어떤 함수의 최대값을 찾는 것은 그 함수의 음수를 취한 후 최소값을 찾는 것과 수학적으로 동일합니다.

  • $L(w,\lambda) = -\frac{1}{2}w^TS_Bw + \frac{1}{2}\lambda(w^TS_Ww -1)$ w에 관해서 미분을 하면 결과는 $-S_Bw + \lambda S_Ww = 0, S_Bw = \lambda S_Ww$

  • $S_W$의 역행렬인 $S_W^{-1}$가 존재해야 합니다. 이 가정은 클래스 내 분산이 모든 방향에 대해 0이 아니라는 것을 의미합니다.

  • 최적화 문제는 $S_w^{-1}S_Bw^* = \lambda w^*$, $w^*$는 행렬 $S = S_W^{-1}S_B$의 고유벡터, $\lambda$는 해당 고유값을 나타냅니다.

  • $w^*$는 S의 고유벡터이며, $\lambda$는 그에 해당하는 고유값입니다. 고유벡터는 데이터를 최적으로 분리하는 새로운 축을 나타내고, 고유값은 그 축의 중요도를 나타냅니다. 즉, $m_0, m_1$ 사이의 차이를 가장 잘 나타내는 방향으로 데이터를 투영하는 벡터입니다.

  • 방향만이 중요하므로, 스케일링을 무시하고 $w^*$를 $S_w^{-1}(m_0 -m_1)$으로 설정할 수 있습니다. 이는 두 클래스 평균 사이의 차이를 클래스 내 분산으로 조정한 것을 의미합니다.

• LDA에서 최적의 discriminant vector $w^*$를 찾은 후, 모든 데이터 인스턴스는 이 새로운 축으로 변화됩니다.

• 판별함수 : $f(x) = w^Tx$로, 주어진 임계값 $\theta_m$에 기반하여 임계값보다 크면 1로 분류하고, 임계값보다 작으면 0으로 분류합니다.

출처

Img_1