[ML] Non-linear Model

Modeling Non-linearity

Feature(basis) Functions

식

• Linear Regression with feature function
  • $f(x) = w_o + \sum_{j=1}^m w_j\phi_j(x)$
• Logistic regression with feature function
  • $f(x) = \sigma(w_0 + \sum_{j=1}^m w_j\phi_j(x))$

장점 : 동일한 학습 알고리즘(Optimization for weight paramteters)을 사용할 수 있습니다. Feature Functions를 통해 데이터를 변환시킨 후에는, 변환된 데이터에 대해 linear model을 적용하여 학습할 수 있습니다.

문제 :

• 문제에 적합한 feature function을 선택하는 것은 쉽지 않습니다.
• 더 많은 feature function을 사용하면 모델의 표현력은 많아지지만, Overfitting의 위험도 증가합니다.
• 더 많은 weight parameters를 학습해야 하기 때문에 계산이 더 많아집니다.

종류

1. 다항식 기저 함수(Polynomial Basis Functions):
   이는 가장 흔히 사용되는 기저 함수 중 하나로, 입력 특성의 다항식을 포함합니다. 여러분이 언급한 것처럼, 이러한 함수들은 ( x^2, x^3, \ldots ) 또는 ( x_1x_2, x_1^2x_2, \ldots )와 같은 항을 포함할 수 있습니다.

2. 가우시안 기저 함수(Gaussian Basis Functions):
   각 기저 함수가 가우시안 함수(정규 분포)의 형태를 갖습니다. 이는 데이터 포인트를 중심으로 '언덕' 모양의 기저를 생성하며, 주로 래디얼 기저 함수 네트워크(RBF 네트워크)에서 사용됩니다.

3. 시그모이드 기저 함수(Sigmoid Basis Functions):
   시그모이드 함수 형태의 기저 함수로, 로지스틱 회귀 분석에서 흔히 볼 수 있습니다.

4. 푸리에 기저 함수(Fourier Basis Functions):
   사인과 코사인 함수의 조합을 사용하여 주기적인 패턴을 모델링합니다.

5. 스플라인 기저 함수(Spline Basis Functions):
   데이터의 구간별로 다항식을 정의하고, 이를 매끄럽게 연결하여 복잡한 패턴을 유연하게 모델링합니다.

6. 웨이블릿 기저 함수(Wavelet Basis Functions):
   웨이블릿 변환을 사용하여 시간-주파수 공간에서 데이터를 분석하고 특징을 추출합니다.

7. 지표 함수(Indicator Functions) 또는 더미 변수(Dummy Variables):
   범주형 데이터를 다룰 때 사용되며, 특정 범주에 속하는지 여부를 나타내는 이진 지표 변수를 생성합니다.

Support Vector Machines

장점 :

• SVM의 learning problem은 linear model의 weight를 배우는 문제와 매우 유사합니다. 이는 커널 함수를 사용하여 데이터를 높은 차원의 공간으로 매핑함으로써 가능해집니다.
• 커널 함수를 사용하면 계산 복잡성을 줄일 수 있습니다. 실제로 고차원으로 데이터를 매핑하지 않고도, 매핑된 고차원에서의 내적을 계산할 수 있습니다.

예시 :

• 주어진 수식은 입력 벡터 $\mathbf{x}$ 를 다항식 커널을 사용하여 변환하는 것을 보여줍니다. 여기서 $\phi(\mathbf{x})$는 입력 벡터를 고차원 공간으로 매핑하는 함수입니다.
• 예를 들어, $\phi(\mathbf{x})$는 $[x_1^2, \sqrt{2}x_1x_2, x_2^2, \sqrt{2}x_1, \sqrt{2}x_2, 1]$와 같이 벡터를 변환합니다. 이 변환을 통해, 원래의 비선형 관계를 고차원에서 선형 관계로 바꿔 SVM이 분류 작업을 수행할 수 있게 됩니다.
• 커널 함수 $K(\mathbf{x}, \mathbf{x'}) = \phi(\mathbf{x})^T \phi(\mathbf{x'})$는 두 벡터의 매핑된 특징 공간에서의 내적을 계산합니다. 이 경우, 다항식 커널은 $(1 + \mathbf{x}^T \mathbf{x'})^2$로 표현될 수 있습니다.

커널 선택의 문제:

• 어떤 커널을 사용할지 결정하는 것은 중요한 문제입니다. 각기 다른 커널은 데이터의 다른 특성을 잡아내며, 모델의 성능과 일반화 능력에 영향을 미칩니다.

• 커널을 선택할 때는 데이터의 특성, 문제의 종류, 계산 효율성 등을 고려해야 합니다. 또한, 커널 선택은 종종 교차 검증과 같은 모델 선택 기법을 통해 이루어집니다.

• 다른 Solution은 Perceptron을 사용하지 말자 $\rarr$ Decision Tree, Naive Bayes, Bayesian Models이 있습니다.

Get Layered

아이디어 :

• 여러 간단한 linear layer를 쌓아올려(non-linear mapping functions)을 모델링합니다.
  • $w^Tx \rarr \sigma(w^Tx)$를 의미합니다.
• linearity로 Non-linearity를 해결할 수 있게 되었습니다.

Neural Network는 여러 층을 통해 신호를 더하고 이때 sigmoid와 같은 non-linear mapping을 사용합니다.

• Input layer $\rarr$ Hidden Layer $\rarr$ Output Layer
• Logistic Regression : Single Layer Perceptron 입니다.
• MLP를 형성합니다.
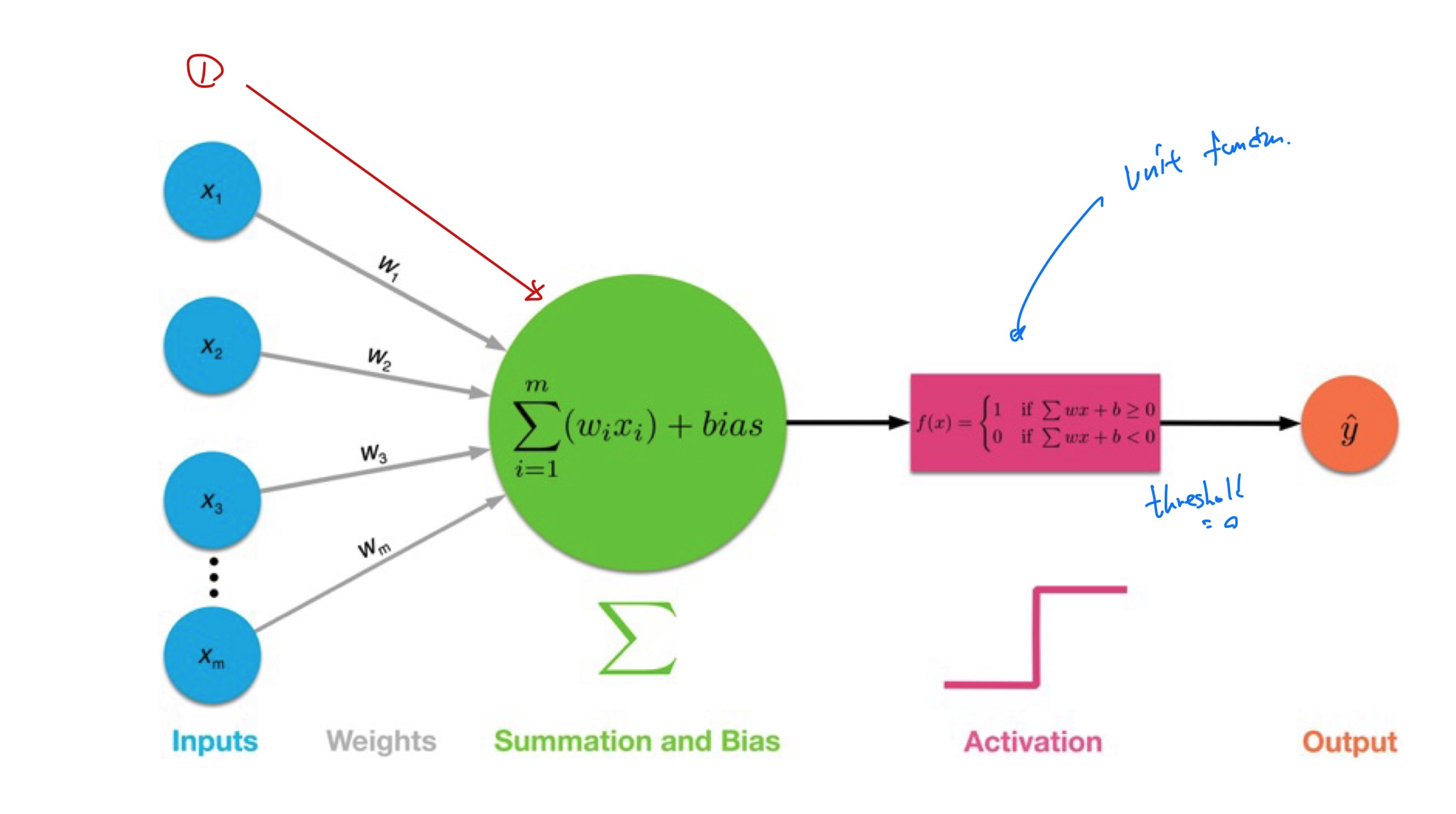
  • Single-Layer-Perceptron : Input Layer와 Output Layer만을 가지며, Hidden layer가 없는 가장 간단한 형태의 인공 신경망입니다. 이 구조에서는 입력이 바로 출력으로 연결되며, 각 입력 $x_i$는 해당하는 가중치 $w_i$와 곱해진 후, 모두 더해져서 출력 뉴런으로 전달됩니다. 이 출력 뉴런은 일반적으로 step function을 activation function으로 사용하며, 특정 임계값을 초과하는 지에 따라 0 또는 1의 값을 출력합니다.
  • Multi-Layer-Perceptron : Input Layer, 하나 이상의 Hidden Layer, Output Layer를 가집니다. Hidden Layer에 있는 각 뉴런은 Input Layer 또는 Hidden Layer의 뉴런으로부터 입력 신호를 받아 가중치와 함께 곱셈을 수행하고, 모두 더해져서 비선형 활성화 함수를 통과하여 다음 층으로 전달됩니다. Feed-forward Neural Network라고도 불립니다. Input은 observable하지만, hidden layer는 cannnot observable합니다.

LogReg	Perceptron
Sigmoid	Activation Function

Activation Functions

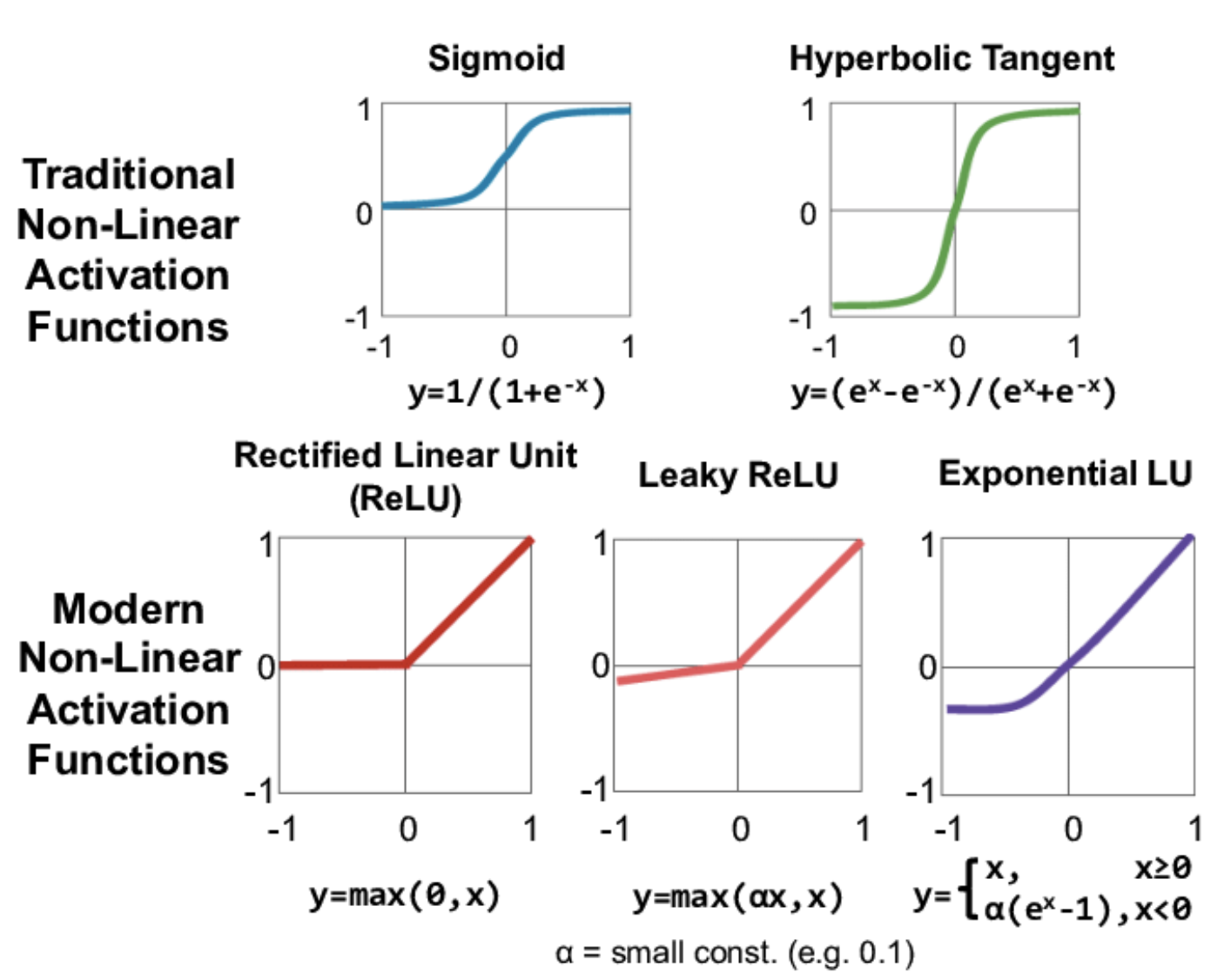
1. 전통적인 활성화 함수:

• 시그모이드(Sigmoid) 함수: $y = \frac{1}{1+e^{-x}}$ 로 표현되며, 출력을 (0, 1) 범위로 제한합니다. 이 함수는 초기 신경망에서 널리 사용되었지만, 기울기 소실 문제(gradient vanishing problem)로 인해 깊은 신경망에서는 덜 사용됩니다.
• 쌍곡선 탄젠트(Hyperbolic Tangent, tanh) 함수: $y = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$ 로 표현되며, 출력을 (-1, 1) 범위로 제한합니다. 이 함수도 시그모이드와 유사하게 기울기 소실 문제가 있을 수 있습니다.

2. 현대적인 활성화 함수:
   • ReLU(Rectified Linear Unit) 함수: $y = \max(0, x)$ 로 표현되며, 음수 입력에 대해 0을, 양수 입력에 대해 그대로 값을 반환합니다. 이 함수는 기울기 소실 문제를 일부 해결하고 계산 효율성이 높아 현대 신경망에서 널리 사용됩니다.
   • Leaky ReLU 함수: $y = \max(\alpha x, x)$로 표현되며, 여기서 $\alpha$ 는 작은 상수(예: 0.1)입니다. 이 함수는 ReLU가 가지는 죽은 뉴런(dead neuron) 문제를 해결하기 위해 음수 입력에 대해 아주 작은 기울기를 부여합니다.
   • ELU(Exponential Linear Unit) 함수: $y = \begin{cases} x & \text{if } x > 0 \\ a(e^{x} - 1) & \text{if } x \leq 0 \end{cases}$로 표현되며, 여기서 $a$는 양수 상수입니다. 이 함수는 음수 입력에 대해 부드러운 포화 상태로 가는 것을 도와 ReLU의 변형으로, 기울기 소실 문제를 더 개선하고 뉴런의 평균 활성화를 근사적으로 0으로 만들어줍니다.

3. 중요한 것은 unit function은 구분할 수 없습니다
   이미지에 설명된 'unit'은 신경망에서 하나의 뉴런을 의미합니다. 신경망에서 각 뉴런(또는 'unit')은 일반적으로 두 부분으로 구성됩니다:

   • 선형 집계(linear aggregation): 이는 여러 입력 $x_i$ 에 대한 가중치 $w_i$ 의 선형 결합과 바이어스 $b$ 를 포함합니다. 수학적으로는 다음과 같이 표현됩니다:
     $z = \sum_{i}(w_i \cdot x_i) + b$

   • 비선형 매핑(non-linear mapping function): 선형 집계를 받아 비선형 활성화 함수를 적용하여 최종 출력을 결정합니다. 이 비선형 활성화 함수는 신경망이 선형적으로 분리 불가능한 패턴을 학습할 수 있게 해줍니다.

   • 이것은 신경망의 구조적 일관성을 유지하기 위한 것으로, 모든 뉴런이 같은 종류의 비선형 변환을 수행합니다. 예를 들어, 신경망의 모든 뉴런이 ReLU 활성화 함수를 사용하면, 이 네트워크의 'unit function'은 ReLU가 됩니다. 다른 활성화 함수를 사용하려면 네트워크를 재설계하거나 다른 네트워크를 선택해야 합니다.

4. Activation Function이 없다면 Multi-layer에서는 어떤 문제가 있을까?

   • Activation Function 없이는 신경망이 XOR문제와 같이 선형적으로 분리할 수 없는 간단한 문제조차 해결할 수 없게 됩니다.
   • layer가 많이 쌓였을 때, 분류할 수 없게 됩니다.
   • non-linear activation function은 신경망이 더 복잡한 함수를 근사할 수 있고, 보다 깊은 이해를 가능하게 하는 feature space로 데이터를 매핑할 수 있게 합니다. activation function이 없으면 신경망은 입력 데이터의 더 깊은 특성을 학습하거나 표현할 수 없습니다.
   • Activation Function이 없는 경우, 신경망의 각 층은 단지 입력에 대한 선형 변환(가중치의 선형 결합과 바이어스의 추가)만을 수행하게 됩니다. 여기서 중요한 점은 선형 변환들의 연속은 결국 하나의 선형 변환으로 간소화될 수 있다는 것입니다.
   • 신경망의 깊이가 모델의 표현력을 증가시키는 주된 이유는 각 층의 비선형 활성화 함수를 통해 입력 데이터를 비선형 공간으로 매핑할 수 있기 때문입니다.

출처

IMG_1
IMG_2