이전 supervised learning에서 Linear Model에 대해 선형 모델로 오류를 최소화하는 모델을 찾는 방법으로 간단하게 넘어갔다. 이번에는 Linear Model에 대해 더 자세히 알아보겠다.
Linear Model(선형 모델)이란,
선형 모델이란 독립 변수(x)와 종속 변수(y) 간 관계가 일차식으로 표현되는 관계를 의미한다. 따라서 선형모델을 단순히 x에 대한 1차 다항식꼴만으로 제한되는 것이 아니라 x의 로그 함수나 exp 함수 등 모두 선형 모델로 표현이 가능하다.
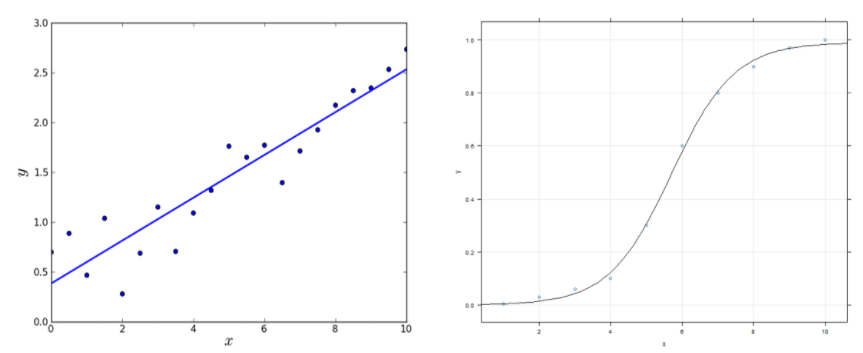
간단히 말해서 머신러닝 공식에서 계수들이 선형결합의 관계에 있는 모델이라 할 수 있다.
선형모델에 대해 기계 학습을 하기 위해, 독립 변수와 종속 변수의 관계를 H(x) = wx + b 꼴로 놓았을 때 이 때 주어진 데이터에 가장 잘 맞는 미지수 w, b의 값을 결정하는 것이 중요한 포인트가 된다.
예제) 학습 시간에 따른 점수의 자료들을 바탕으로 학습 시간에 따른 점수를 예측해보자(Linear Model을 통해)
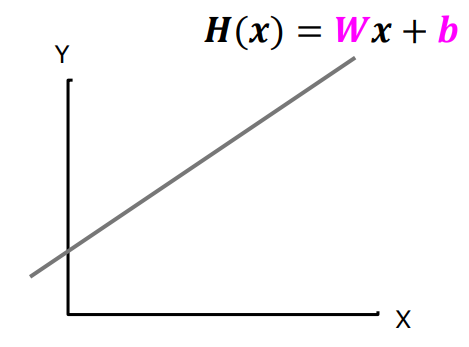
위의 학습 시간(x)에 따른 점수(y)의 식을 H(x) = wx + b 라고 하자. 이 때 목표는 주어진 데이터에 가장 잘 맞는 미지수 w와 b의 값을 찾는 것이다. H(x)값인 직선 식의 예상값과 원래 데이터 y값의 차이는 오류(cost/loss)라고 한다. 이를 전체 학습 데이터 m개에 대한 cost function식으로 나타내면
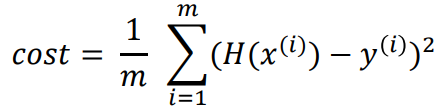
이 때 우리의 목표는 오류인 cost가 최소가 되는 미지수 w, b의 값을 결정하는 것이다. 다음은 w값에 따라 변화하는 cost function의 그래프를 나타낸 것이다.
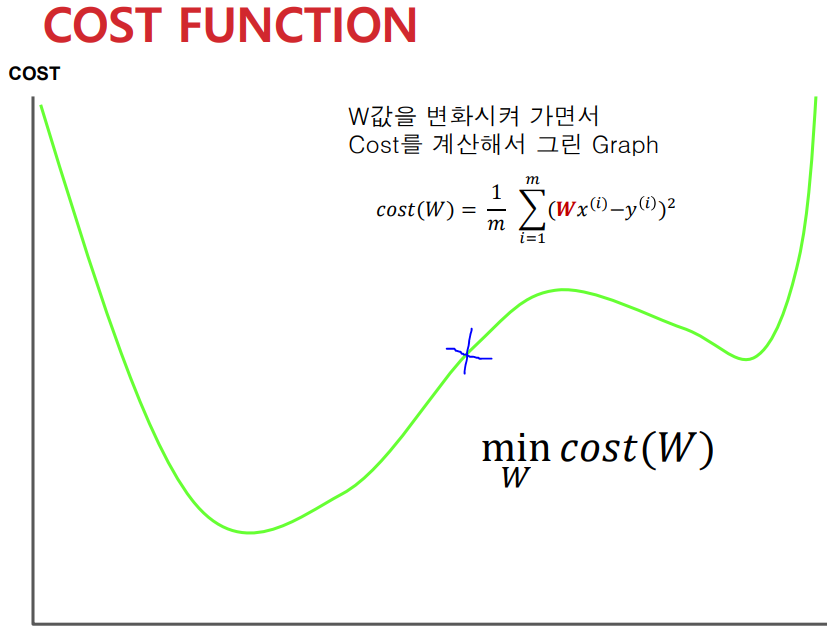
Gradient Descent(경사하강법)
Gradient descent는 함수 값이 낮아지는 쪽으로 x값을 바꾸며 최종적으로 최소의 함수값을 갖도록 하는 방법이다. 원래 함수의 최소를 구하려면 미분을 이용해 미분계수가 0인 지점을 기점으로 달라지는 것을 파악하면 되지만, 경사하강법을 통해 함수의 최솟값을 찾는 주된 이유는 데이터양이 매우 큰 경우 미분 계수를 계산하는 것보다 경사하강법을 사용하는 편이 더 효율적이고 쉽게 구현할 수 있기 때문이다.
임의의 점 p에서의 접선의 기울기가
- 양(그래프가 증가하는 중)이라면 p의 왼쪽으로 이동,
- 음(그래프가 감소하는 중)이라면 p의 오른쪽으로 이동하여 최소의 함수값을 갖는 쪽으로 유도한다.
이를 위의 cost function 그래프에 대입해 살펴보자. 그래프는 H(x)의 미지수 w에 따른 cost값이다. 그래프의 파란 점에서 시작한다고 했을 때 이 때 해당 w좌표에 대한 접선의 기울기는 양이므로 왼쪽으로 계속 이동하다 최소의 함수값을 발견하게 된다.
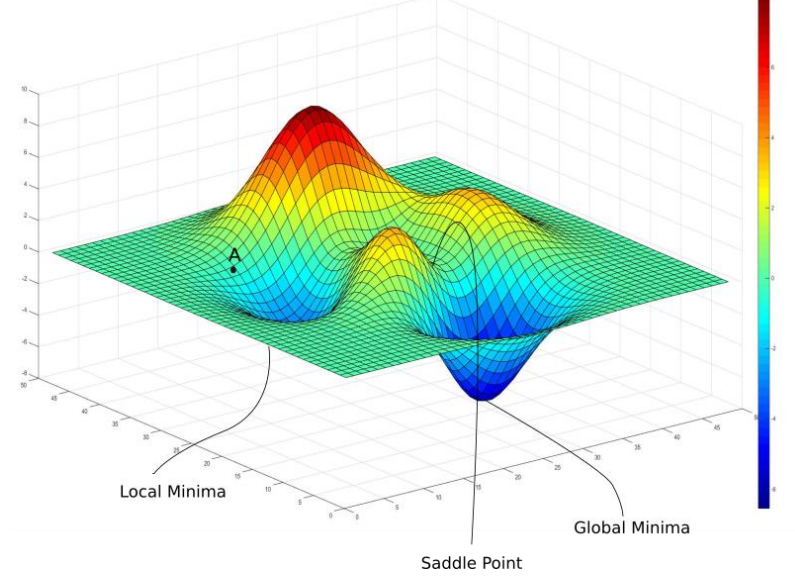
이런 식으로 임의의 점에 대한 경사하강법을 적용한 최솟값(local minimum)을 구하였다. 하지만 구하고자 하는 것은 함수 전체에 대한 최솟값(global minimum)이다. 이렇게 그래프의 다른 쪽에 처음에 임의로 선택한 점보다 더 최소의 값을 갖는 부분도 있을 수 있기에 언제나 함수의 최솟값을 구하는 알고리즘은 아니다.
이렇게 간단한 선형 모델에서의 cost와 이를 기반으로 경사 하강법을 적용해보았다. 다음에도 선형 모델에 대해 더 알아보겠다.