Deep_Learning의 요약
- 딥러닝의 개요부터 모델 구성과 학습 방법을 위한 기법까지 전체적으로 요약해봅니다
- 실습 전체 코드는 마지막에 접어 두겠습니다
<목 차>
- 딥러닝이란?
- 텐서(Tensor) 표현과 연산
- 딥러닝 구조와 모델
- 딥러닝 모델 학습
Next Chapter
- 모델 저장과 콜백(save & callback)
- 모델 학습 기술
- 모델 크기 조절과 규제
- 가중치 초기화와 배치 정규화(Batch Normalization)
<시작하기 전에 인공 지능/머신러닝/딥러닝의 차이를 시각화 해서 보자>
1. 딥러닝이란?
1) 인공 신경망(Artificail Neural Network)
인간의 신경 전달 물질인 신경세포(Neuron)간의 신호 전달 방법을 기반으로 구현 된 신경망(Network)
입력층인 input 층, 전달하는 은닉층 hidden 층, 출력층인 Output 층 으로 구성되어 있습니다
hidden 층은 목적에 맞게 여러 층으로 구성할 수 있습니다
2) 인공 신경망의 역사
'퍼셉트론' 이라는 입력층과 출력층으로 구성 되어 있는 기본 Network에서 출력 이전에 활성화 함수(Activation function) 을 통해 정보를 전달하는 구조부터 시작 하였습니다.
퍼셉트론이 여러 층으로 이루어진 '다층 퍼셉트론' 부터 신경망(Network)라 불립니다
(활성화 함수로 계단함수를 활용하다가 비선형성을 도입하면서 활성화 함수로 연속적인 함수들을 사용 시작)
사람의 신경세포 신호 전달 과정 중 시냅스의 흥분/억제 상태에 따라 임계치를 넘어야 신호가 넘어가지는 과정을 모방하였습니다. (활성화 함수)
3) 딥러닝 역사
위 인공 신경망으로 결과를 예측하는 것은 사람의 설정 부분이 들어가고 복잡하지 않은 Layer로 구성되어 있다

- 그림에서 특징 추출(Feature extraction)는 이미지 딥러닝 과정에서 나오는 기법
딥러닝 부터는 데이터가 주어지면 복잡한 인공 신경망으로 컴퓨터가 스스로 학습과 특징 추출을 함께 수행 합니다.

사람의 개입이 적어져서 편견과 오류가 줄어들고 효율적으로 학습 시킬 수 있으나 많은 데이터와 매개변수가 필요하기 때문에 많은 비용과 시간을 필요로 합니다. (Cost가 큽니다)
2. 텐서(Tensor) 표현과 연산
1) 텐서(Tensor)
텐서(Tensor) 는 데이터를 담기위한 컨테이너(container)로서 다차원 배열 또는 리스트 형태와 유사합니다. 일반적으로 수치형 데이터를 저장하고, 동적 크기를 가집니다. 텐서플로우(TensorFlow)는 데이터 표현과 다양한 수학식을 계산하기 위한 기본 구조로 텐서를 사용해서 표현합니다.
텐서는 형상이 존재하며 데이터의 표현에 따라서 사용합니다. 사용되는 용어는 다음과 같습니다.
- Rank : 축(차원)의 개수
- Shape : 형상(각 축의 요소와 개수)
- Type : 데이터 타입(int, float, bool 등)
<0차원 ~ 6차원까지 Tensor의 시각화>
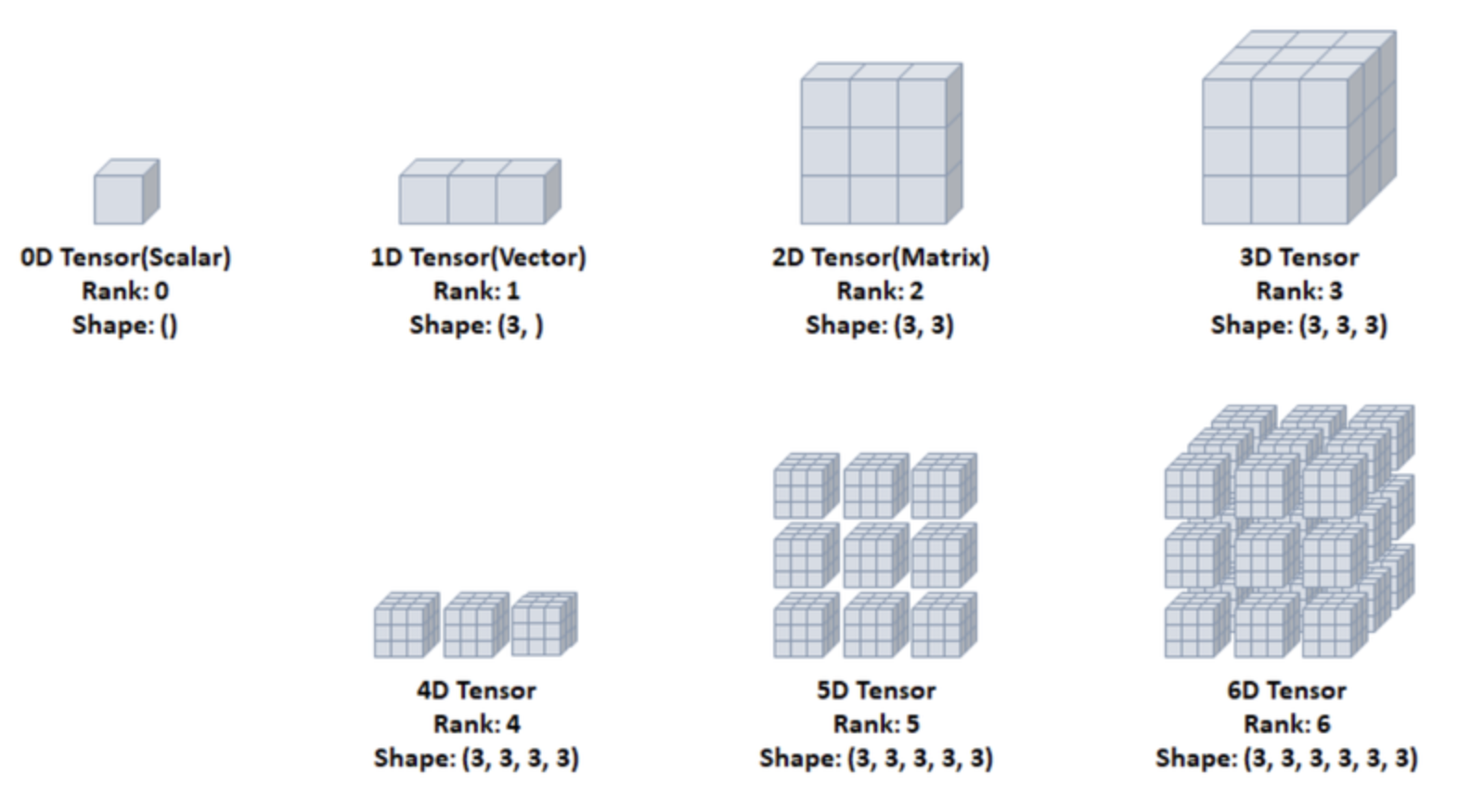
- 그림에서 축(Rank)이 늘어나면서 차원이 늘어나는 것을 시각화 했습니다
예제) (3,3,3)의 3D Tensor를 만들고 위 그림처럼 차원을 반환해보세요
코드 답# 3차원 텐서 생성 t3 = tf.constant([ [[1,2,3],[4,5,6],[7,8,9]],[[10,11,12],[13,14,15],[16,17,18]], [[19,20,21],[22,23,24],[25,26,27]] ]) # 출력 print(t3) # 차원 반환 print(tf.rank(t3))
2) 텐서 타입 및 변환
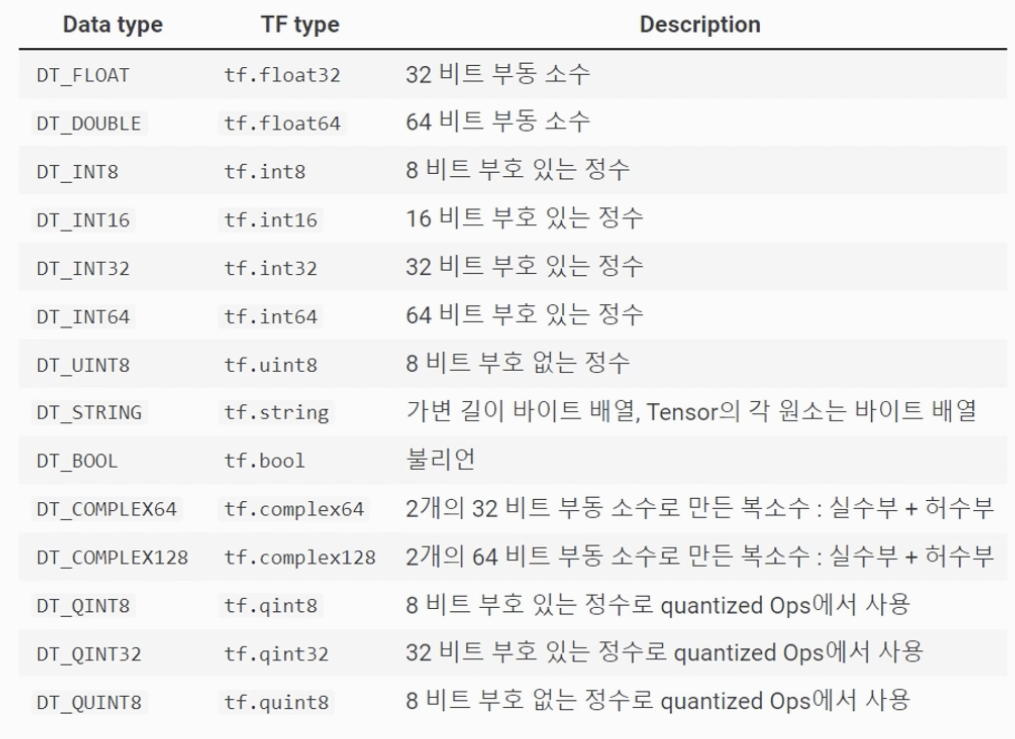
텐서의 기본 데이터 타입(dtype)은 정수형(int32), 실수형(float32), 문자열(string) 등이 있고, 그 외에도 여러 데이터 타입 등이 존재합니다.
<Type 사진>
<텐서 타입을 지정해서 저장 코드>
f16 변수에 2.0이라는 float16 타입의 실수를 저장해보는 코드
# Tensor type 지정
f16 = tf.constant(2. , dtype=tf.float16)2-1) 텐서 변환
텐서의 타입을 변환하고자 할 때는 tf.cast를 사용합니다. 여기서는 16비트 실수형 tf.float16을 32비트 실수형 tf.float32로 변환하였습니다.
f32 = tf.cast(f16, tf.float32)
print(f32)2-1-1) 텐서 변환 정리
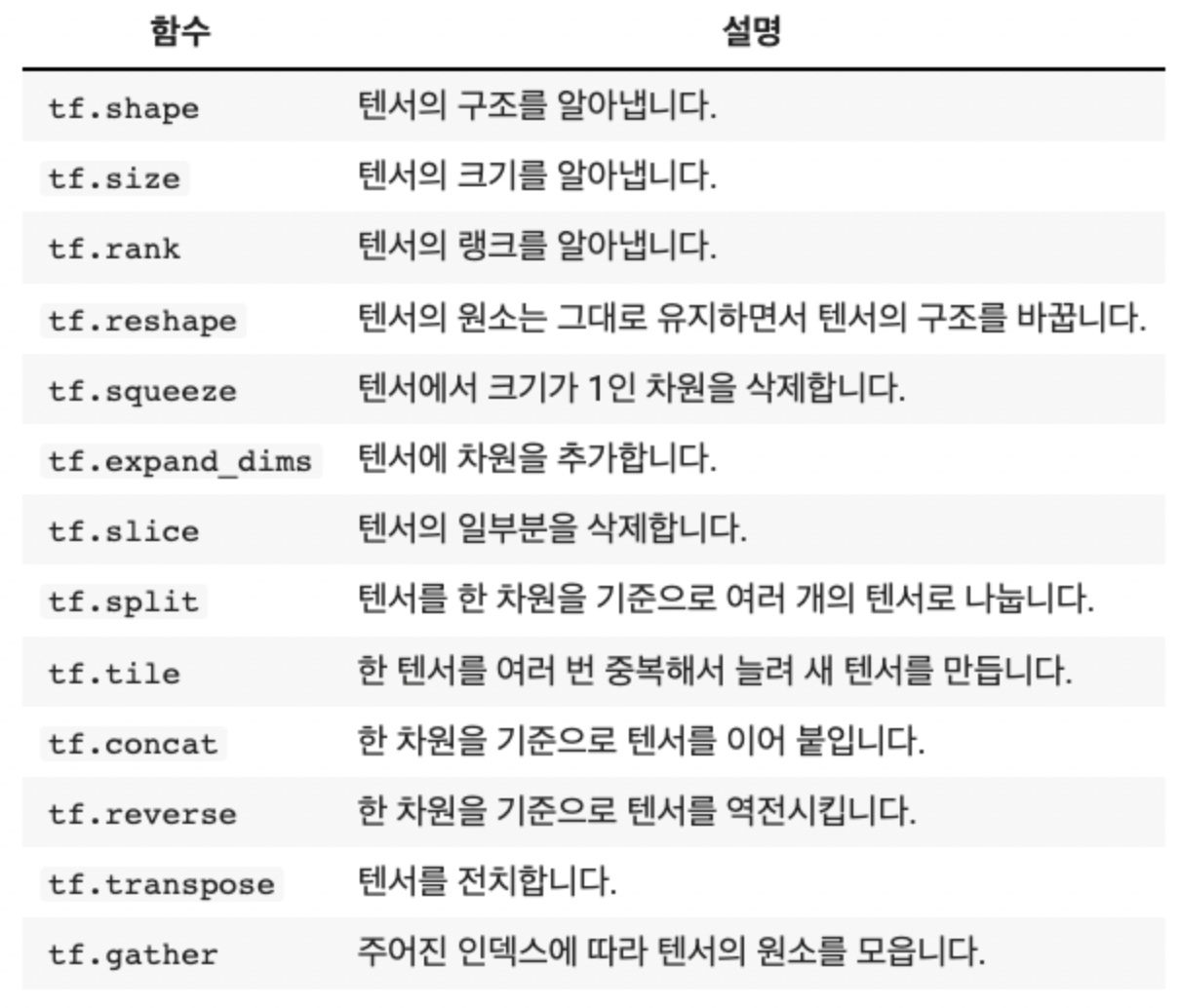
3) 텐서 연산
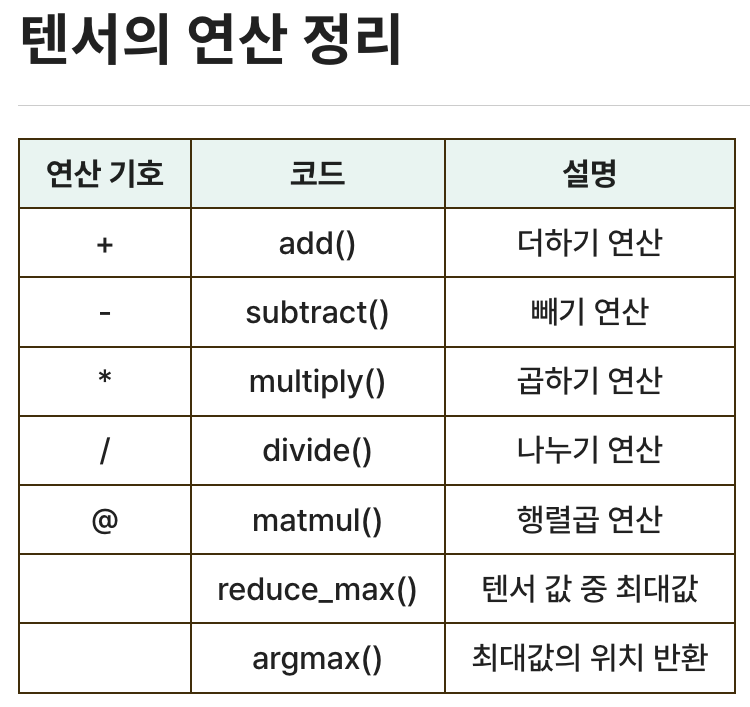
텐서끼리의 연산은 사칙연산과 연산자들로 할 수 있습니다. 단, Type이 같은 텐서끼리 연산이 가능합니다
2차원 이상부터는 대응하는 요소끼리 연산을 할 수 있습니다(예시. 행렬의 연산)
3. 딥러닝 구조와 모델
1) 모델의 구조와 레이어
-
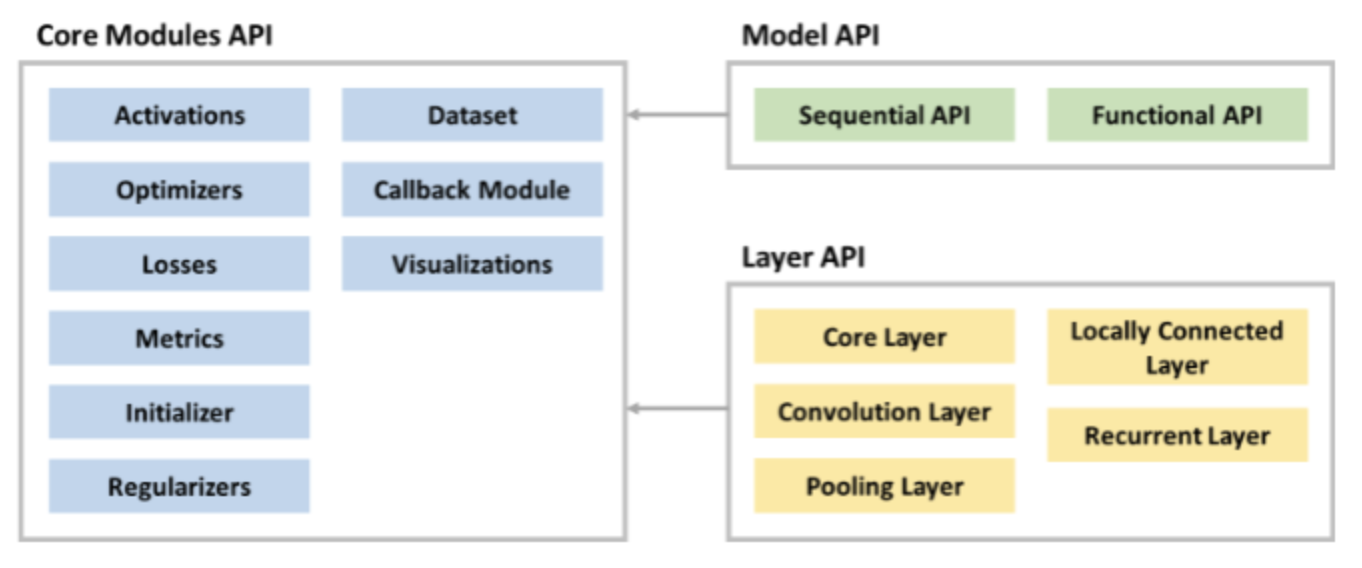
모델의 구조
Model API & Layer API가 있고 필요한 모듈들을 Modules API를 호출하여 사용합니다
-
레이어
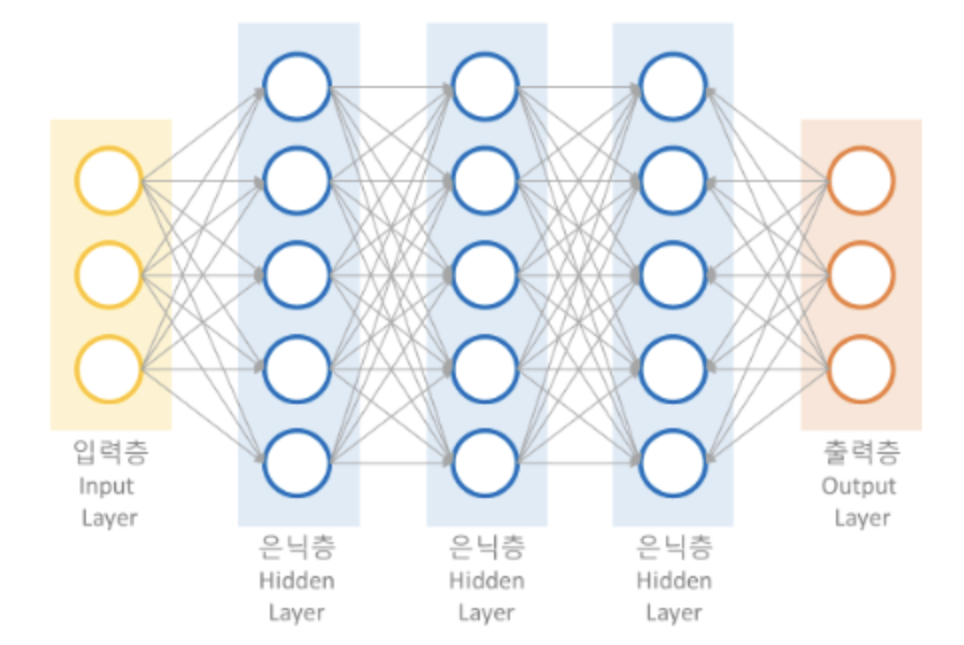
딥러닝은 여러 개의 레이어(Layer)로 구성되어 있으며, 기본적으로 입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer) 으로 구분됩니다. 레이어는 딥러닝 모델을 구성하는 핵심 데이터 구조로서 하나 이상의 텐서를 입력받아 하나 이상의 텐서를 출력하는 데이터 처리 모듈입니다.
<Input 레이어>
입력 사이즈(shape)을 지정하고, type과 batch_size, Layer name을 지정할 수 있다
keras.Input(shape=(28, 28), dtype=tf.float32, batch_size=16, name='input')<Dense 레이어>-완전 연결 계층
히든 레이어 겹겹이 쌓을 수 있는 층이고, 유닛(뉴런)수와 활성화 함수, 이름까지 지정할 수 있다
layers.Dense(10, activation='relu', name='Dense Layer')<Flatten 레이어>
입력 데이터의 크기를 배치 크기(데이터 크기)를 제외하고 데이터를 1차원 벡터로 평평하게 변환합니다
# 코드는 28 x 28 x 1 의 크기를 일렬 벡터로 변환
layers.Flatten(input_shape=(28, 28, 1))(inputs)2) 딥러닝 모델
모델 구현 방법
- Sequential() 함수 활용한 Sequential API
- Functional API
- Subclassing API
a. Sequential API
Sequential API를 이용하는 방법은 모델이 순차적인 구조로 진행할 때 사용하는 간단한 방법입니다. 다만 이 방법은 다중 입력 및 출력이 존재하는 등의 복잡한 모델을 구성할 수 없습니다.
Sequential API를 이용한 방법 중 첫번째는 Sequential 객체 생성 후,add()를 이용하여 사용할 레이어들을 추가하는 방법입니다.
코드 예시 펼쳐주세요.. model = models.Sequential()
model.add(layers.Input(shape=(28, 28)))
model.add(layers.Dense(300, activation='relu'))
model.add(layers.Dense(100, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.summary()b. Functional API
모델 생성에 Functional API를 이용하는 방법은 가장 권장되는 방법입니다. Functional API는 딥러닝 모델을 복잡하고, 유연하게 구성하는 것이 가능하며, 다중 입출력을 다룰 수 있습니다.
이전 층에서 변수를 선언해서 각 층마다 전달받는 방식(함수처럼)
inputs = layers.Input(shape=(28, 28, 1))
x = layers.Flatten(input_shape=(28, 28, 1))(inputs)
x = layers.Dense(300, activation='relu')(x)
x = layers.Dense(100, activation='relu')(x)
x = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=inputs, outputs=x)
model.summary()c. Subclassing API
서브클래싱(Subclassing) 방법은 커스터마이징에 최적화된 방법으로, Model 클래스를 상속받아서 사용하고 모델에 포함되는 다음과 같은 기능을 사용할 수 있습니다.
- fit() : 모델 학습
- evaluate() : 모델 평가
- predict() : 모델 예측
- save() : 모델 저장 (파일은 나중에 형식마다 다른 명령어 배울거에요)
- load() : 모델 불러오기 (위와 마찬가지)
- call() : 메소드 안에서 원하는 계산 가능
Subclassing API를 사용하면 Functional API로도 구현할 수 없는 모델들도 구현이 가능하지만, 객체지향 프로그래밍(Object-oriented Programming)에 익숙해야 합니다.
코드 예시 펼쳐주세요..class MyModel(models.Model):
def __init__(self, units=30, activation='relu', **kwargs):
super(MyModel, self).__init__(**kwargs)
self.dense_layer1 = layers.Dense(300, activation=activation)
self.dense_layer2 = layers.Dense(100, activation=activation)
self.dense_layer3 = layers.Dense(units, activation=activation)
self.output_layer = layers.Dense(10, activation='softmax')
def call(self, inputs):
x = self.dense_layer1(inputs)
x = self.dense_layer2(x)
x = self.dense_layer3(x)
x = self.output_layer(x)
return x<문제 풀어보기 1.>, Seqential API 모델 만들어 보기
(100,100,3) 형태의 데이터를 받는 Input layer
Flatten layer
hidden layer (뉴런 400, 200, 100, 활성화 함수는 각각 relu,relu,softmax 사용)
model = models.Sequential()
# (100, 100, 3) 형태의 데이터를 받는 Input 레이어를 쌓으세요.
# [[YOUR CODE]]
model.add(layers.Input(shape=(100, 100, 3)))
# Flatten 레이어를 쌓으세요.
# [[YOUR CODE]]
model.add(layers.Flatten())
# Unit의 수는 400, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
# [[YOUR CODE]]
model.add(layers.Dense(400, activation='relu'))
# Unit의 수는 200, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
# [[YOUR CODE]]
model.add(layers.Dense(200, activation='relu'))
# Unit의 수는 100, 활성화함수는 Softmax를 사용하는 Dense 레이어를 쌓으세요.
# [[YOUR CODE]]
model.add(layers.Dense(100, activation='softmax'))
model.summary()<문제 풀어보기 2.>, functional API 모델 만들어 보기
(100,100,3) 형태의 데이터를 받는 Input layer
Flatten layer
hidden layer (뉴런 400, 200, 100, 활성화 함수는 각각 relu,relu,softmax 사용)
# (100, 100, 3) 형태의 데이터를 받는 Input 레이어를 쌓으세요
inputs = layers.Input(shape=(100,100,3))
# Flatten 레이어를 쌓으세요.
x = layers.Flatten()(inputs)
# Unit의 수는 400, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
x = layers.Dense(400, activation='relu')(x)
# Unit의 수는 200, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
x = layers.Dense(200, activation='relu')(x) # 이 부분에 x를 연결해주어야 합니다.
# Unit의 수는 100, 활성화함수는 Softmax를 사용하는 Dense 레이어를 쌓으세요.
x = layers.Dense(100, activation='softmax')(x)
model = models.Model(inputs = inputs, outputs = x)
model.summary()
model.summary()<문제 풀어보기 3.>, Subclassing API 모델 만들어 보기
(100,100,3) 형태의 데이터를 받는 Input layer
Flatten layer
hidden layer (뉴런 400, 200, 100, 활성화 함수는 각각 relu,relu,softmax 사용)
class YourModel(models.Model):
def __init__(self, **kwargs):
super(YourModel, self).__init__(**kwargs)
# Flatten 레이어를 쌓으세요.
self.flat_layer = layers.Flatten()# [[YOUR CODE]]
# Unit의 수는 400, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
self.dense_layer1 = layers.Dense(400, activation='relu') # [[YOUR CODE]]
# Unit의 수는 200, 활성화함수는 ReLU를 사용하는 Dense 레이어를 쌓으세요.
self.dense_layer2 = layers.Dense(200, activation='relu') # [[YOUR CODE]]
# Unit의 수는 100, 활성화함수는 Softmax를 사용하는 Dense 레이어를 쌓으세요.
self.output_layer = layers.Dense(100, activation='softmax')# [[YOUR CODE]]
def call(self, inputs):
# Flatten 레이어를 통과한 뒤 Dense 레이어를 400 -> 200 -> 100 순으로 통과하도록 쌓으세요.
x = self.flat_layer(inputs)# [[YOUR CODE]]
x = self.dense_layer1(x) # [[YOUR CODE]]
x = self.dense_layer2(x) # [[YOUR CODE]]
x = self.output_layer(x) # [[YOUR CODE]]
return x
# (100, 100, 3) 형태를 가진 임의의 텐서를 생성해줍니다.
data = tf.random.normal([100, 100, 3])
# 데이터는 일반적으로 batch 단위로 들어가기 때문에 batch 차원을 추가해주겠습니다.
data = tf.reshape((-1, 100, 100, 3))
model = YourModel()
model(data)
model.summary()4. 딥러닝 모델 학습
1) 손실 함수(Loss Function)
학습 : 최적화 된 매개변수를 찾아가는 것
손실함수란 위 학습을 얼마나 잘 되고 있는지에 대한 지표! (값을 줄여가는 방향으로 가야 합니다)
<손실함수의 종류>
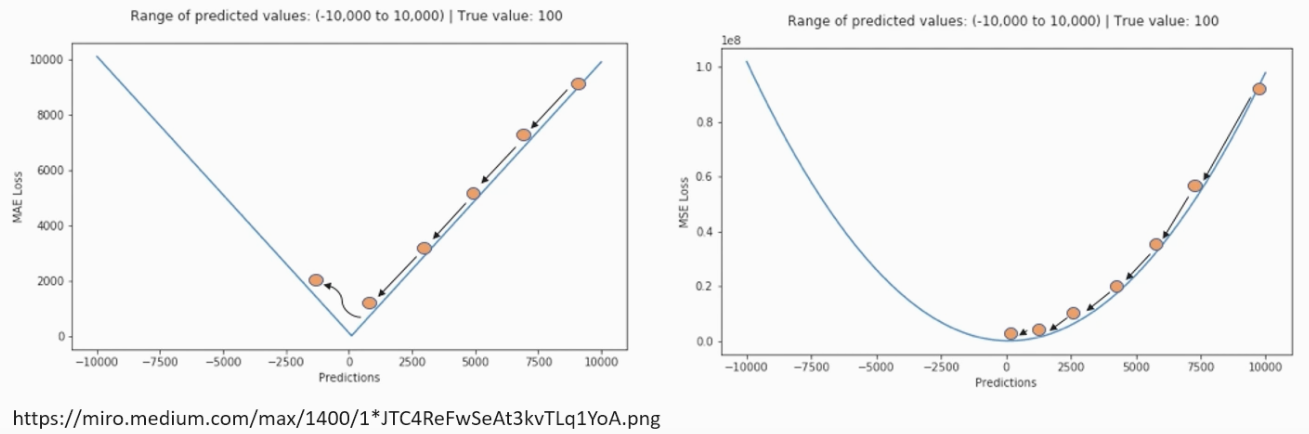
1) MAE (Mean Absolute Error) : 오차 간의 절대값의 평균을 이용한 손실 함수, 오차가 커져도 일정하게 증가, 이상치에 강건한 특성, 일반적으로 회귀 문제에 사용됩니다
2) MSE (Mean Squared Error) : 오차 간 차이의 제곱값의 평균을 이용한 손실 함수, 제곱값을 사용하기 때문에 오차가 커질수록 손실함수가 크게 증가하고 오차가 클수록 큰 페널티를 부여합니다. 많이 쓰이고 일반적으로 회귀 문제에 사용합니다!
- 좌측 MAE, 우측 MSE
3) CEE (Cross Entropy Error) : 크로스 엔트로피(Cross-Entropy)는 주로 분류 문제에서 사용되는 손실 함수 중 하나로, 예측값과 실제 타깃 값 사이의 유사성을 측정합니다(log와 e자연상수 사용). 분류 문제에서 모델이 얼마나 잘 예측하고 있는지를 평가하는 데 사용됩니다. 정답에 가까울수록 0에 가까워지고 오답에 가까울수록 음의 방향으로 발산 합니다 아래 세가지 손실함수로 문제에 맞게 사용합니다
크로스 엔트로피 손실 함수는 모델을 훈련할 때 예측값과 실제 타깃 값 사이의 차이를 줄이는 데 사용됩니다. 모델이 정확한 예측을 하면 크로스 엔트로피 값은 작아지며, 모델의 성능이 좋아집니다. 반대로, 모델이 부정확한 예측을 하면 크로스 엔트로피 값은 커지며, 모델의 성능이 나빠집니다. 이를 최소화하는 것이 분류 모델의 학습 목표 중 하나입니다.
4) categorical_cross_entropy : 다중 분류, 범주형 손실함수 (클래스가 0,1 이루어진)
5) sparse_categorical_entropy : 다중 분류, (배타적 방식으로 (0,1,2,3~)으로 이루어진)
6) binary_crossentropy : 이진분류로 이루어진 클래스
1-1) One_hot_Encoding
정답인 레이블만 1로 표현하고 나머지는 0으로 채우는 인코딩 방식입니다. 예를 들어 한 피처에 사과, 수박, 참외가 있으면 사과는 (1,0,0) 수박은 (0,1,0) 참외는 (0,0,1)로 인코딩 합니다
2) 옵티마이저(Optimizer)와 지표
손실 함수를 기반으로 모델이 어떻게 업데이트 되어야 하는지 결정 해줍니다. 가장 적절한 최적화 된 매개변수를 찾는 것이 옵티마이저 입니다. (손실함수의 값이 최소값이 되는 매개변수)
-
경사하강법
손실함수를 미분한 값(기울기)을 통해 방향에 따라 감소시키면서 스텝(학습률)마다 최소값을 찾아가는 기법
학습률(learning_rate, lr) : 에타로 표현하고 미분값의 곱으로써 계산하고 학습을 얼마나 시킬지 결정하는 하이퍼 파라미터 (보폭) -
학습률 (Learning Rate)
모델을 학습하기 위해서 적절한 학습률을 지정해줘야 한다
Lr이 너무 크면 발산하고, 너무 작으면 최소값에 도달할 수가 없다. lr이 너무 작으면 epoch을 크게 해야한다.
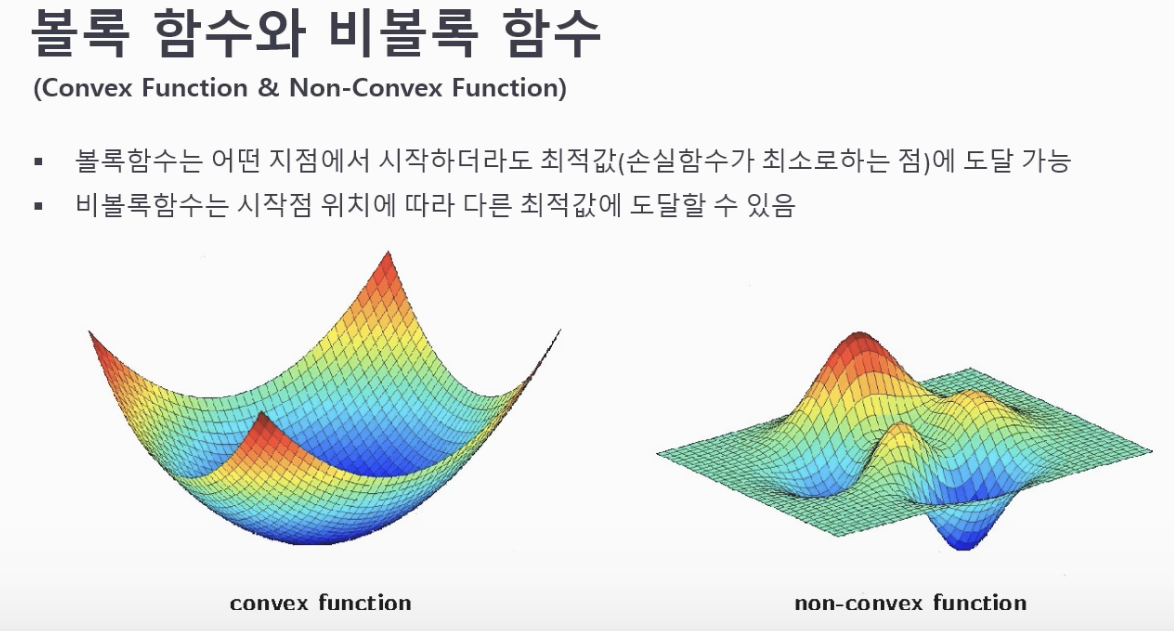
<Convex Function & Non-Couvex Function> 볼록함수와 비볼록 함수
시작점 위치에 따라 다른 최적값에 도달을 볼 수 있는 그림(초기값과 연관 지어 생각할 수 있다)
2-1) 옵티마이저의 종류
- SGD (확률적 경사 하강법) : 단순하고 계산이 빠르나, 미분값의 진동폭이 크고 연속적 표현이 불가능하여 개선해서 기법들을 만듬
- 모멘텀 : v 속도의 개념을 추가하여 모멘텀 상수(평균,분산)을 통해 이전 기억을 가져가며 최소값 도달
- AdaGrad : 학습률을 감소시키면서 최소값의 도달, 입력된 순서에 비중을 주느 개선 된 RMSprop 방식 있음
- Adam : 모멘텀과 AdaGrad의 장점을 모아 많이 사용하는 방식
3) 딥러닝 모델 학습
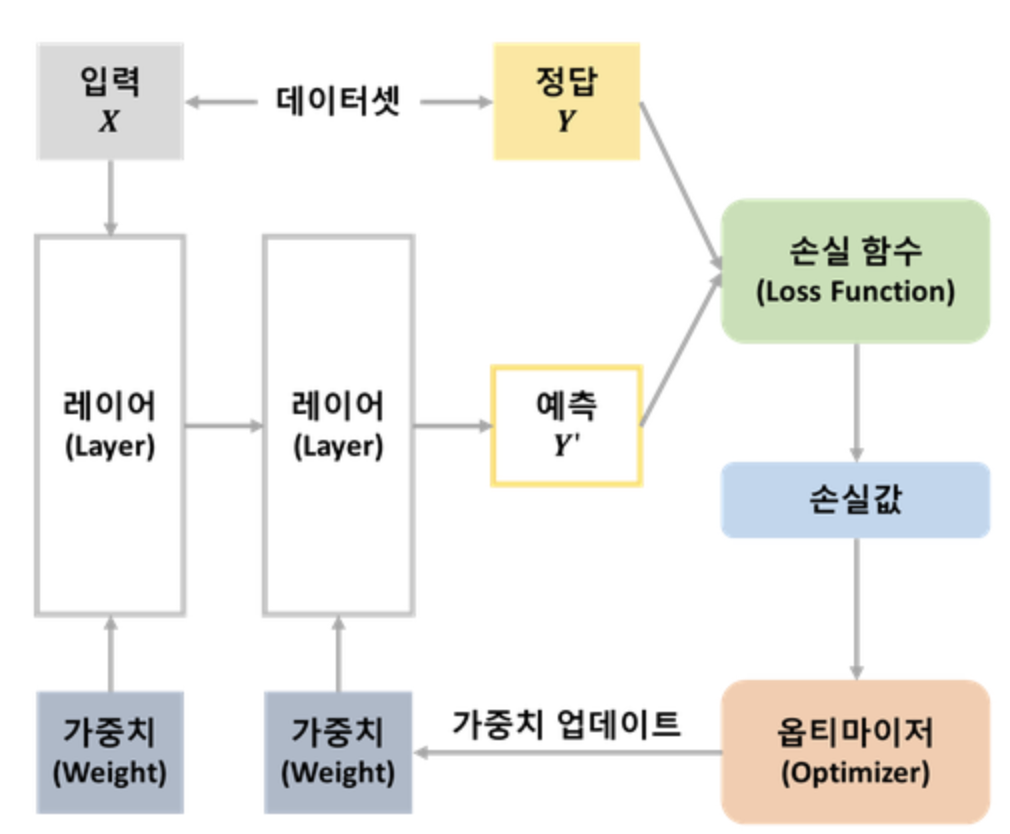
<딥러닝의 전체 과정 그림>
데이터 생성
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=200, n_features=1,
bias=5.0, noise=5.0, random_state=123)
y = np.expand_dims(y, axis=1)
plt.scatter(X, y)
plt.show()데이터 분리
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y,
test_size=0.2,
shuffle=True,
random_state=123)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)모델 생성
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import models, layers, optimizers, utils
model = keras.Sequential()
model.add(layers.Dense(1, activation='linear', input_shape=(1,)))
model.summary() 모델 학습
# 모델 컴파일
optimizer = optimizers.SGD()
model.compile(loss='mse', optimizer=optimizer, metrics=['mae', 'mse'])
history = model.fit(x_train, y_train, epochs=40) 모델 평가
model.evaluate(x_test, y_test)모델 예측
result = model.predict(X)