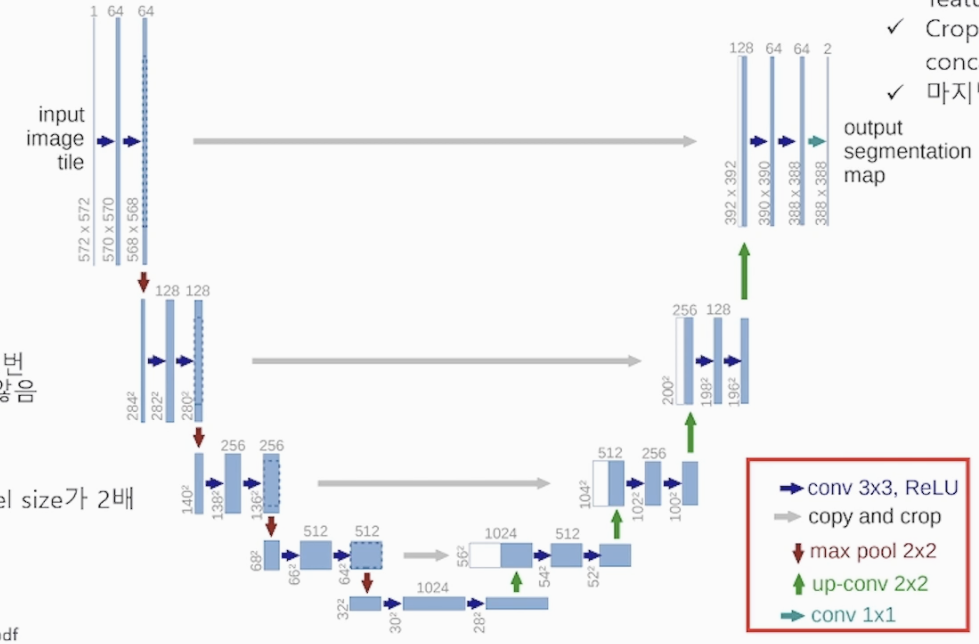
Deep.Learngin from Scratch 밑시딥 1권
(1권은 이미지 분류/CV 분야 위주로 구성 되어 있습니다)
(코드적 구현은 따로 작성할 예정 입니다)
(책 내용 그대로 옮기기 보단 저자가 공부하면서 중요한 부분 요약 위주로 작성 했습니다)
- 목 차
- 헬로 파이썬 (생략)
- 퍼셉트론
- 신경망
다음 chapter
4. 신경망 학습
5. 오차역전파법
- 학습 관련 기법들
last chapter
7. 합성공 신경망(CNN : Convolution Neural Network)
8. 딥러닝
1. 헬로 파이썬(생략)
2. 퍼셉트론
개념을 완벽하게 이해하고 넘어가는게 좋습니다!
2-1) 단층 퍼셉트론 (1층으로 이루어진 퍼셉트론, input > output)
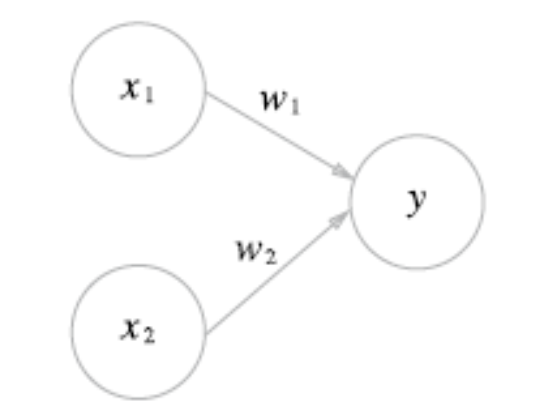
- 퍼셉트론(인공 뉴런) : 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 알고리즘, 신호=흐름
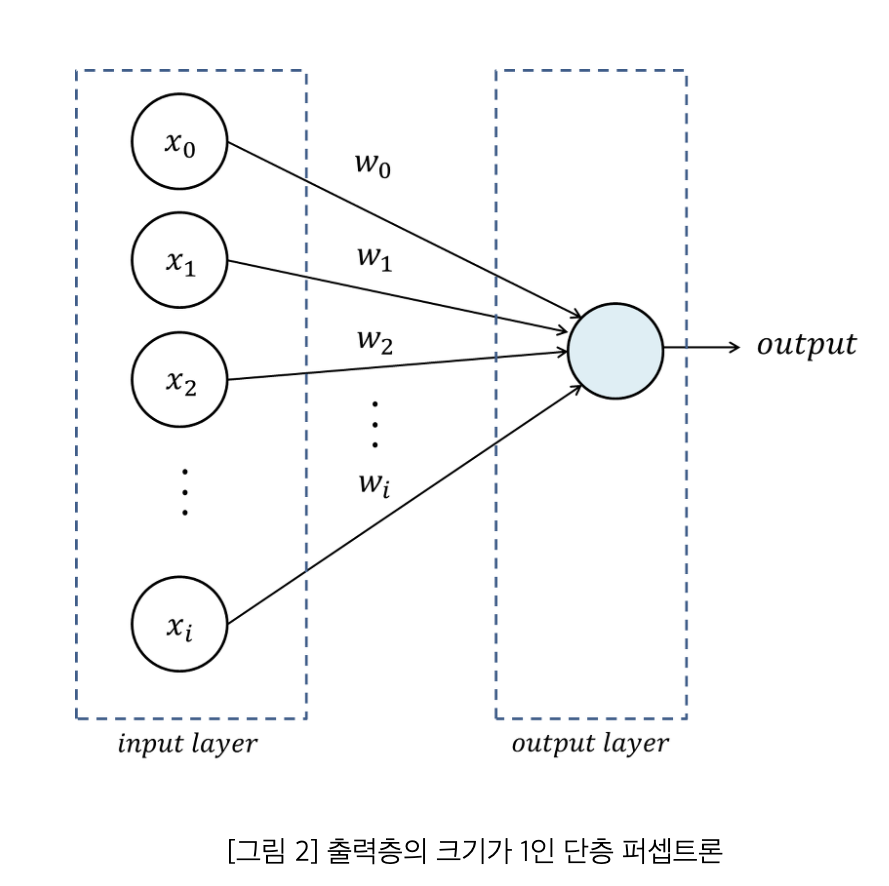
-
뉴런 or 노드 : 각각 위 그림의 원
-
가중치 : 입력신호 x 데이터가 출력 노드로 보내질 때, 각각의 고유한 곱해지는 매개변수 W(weight), 각 뉴런의 영향력을 제어합니다
-
임계값(세타) : 입력신호의 총합이 한계(임계값)을 넘어야 1을 출력
(임계값을 넘어가서 출력되는 것을 '뉴런이 활성화' 라고 표현한다) -
편향(bias) : 임계값을 좌변으로 옮겨서 0으로 만들고 추후 활성화를 조절해 주는 변수(-세타 = b로 치환), 뉴런(노드)의 활성화의 정도를 제어합니다
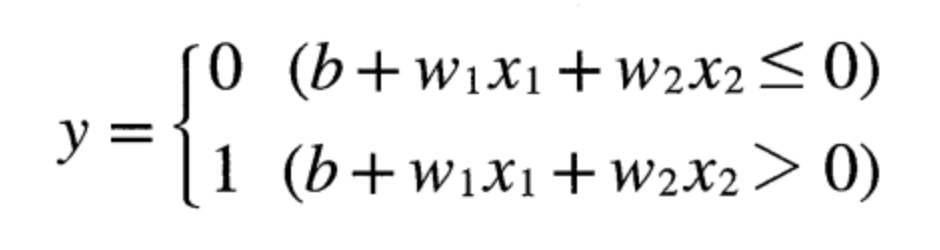
(그림에서 w1,w2는 가중치, b는 편향 각 매개변수는 출력에 영향력과 활성화 정도를 조절)
2-2) 단순 논리 회로 (2개의 입력 신호 기준)
(0,1로 입력 신호와 출력 신호의 대응표인 '진리표'로 표현한다)
- AND 게이트 : 입력이 둘다 '1'일 때 출력이 '1' 그 외에 경우는 전부 '0'을 출력한다
- NAND 게이트 : Not AND 위 AND 게이트 출력의 대우
- OR 게이트 : 두 입력 신호 중 1개라도 '1'일 경우 '1'출력, 둘다 '0'일 경우 0 출력
여기까지로 w,세타(임계점) 사람이 직접 세팅 해보는 것 연습
2-3) 선형과 비선형
-
선형 : 직선으로 표현할 수 있는 영역
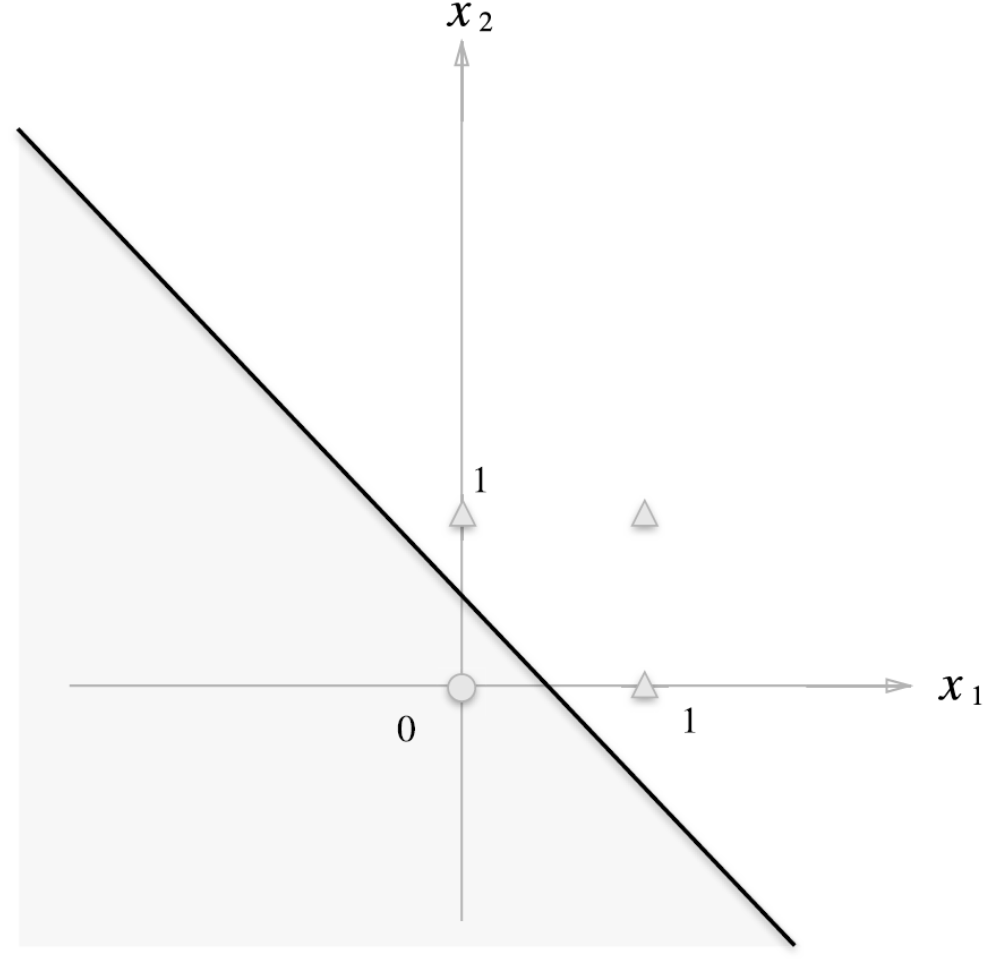
-
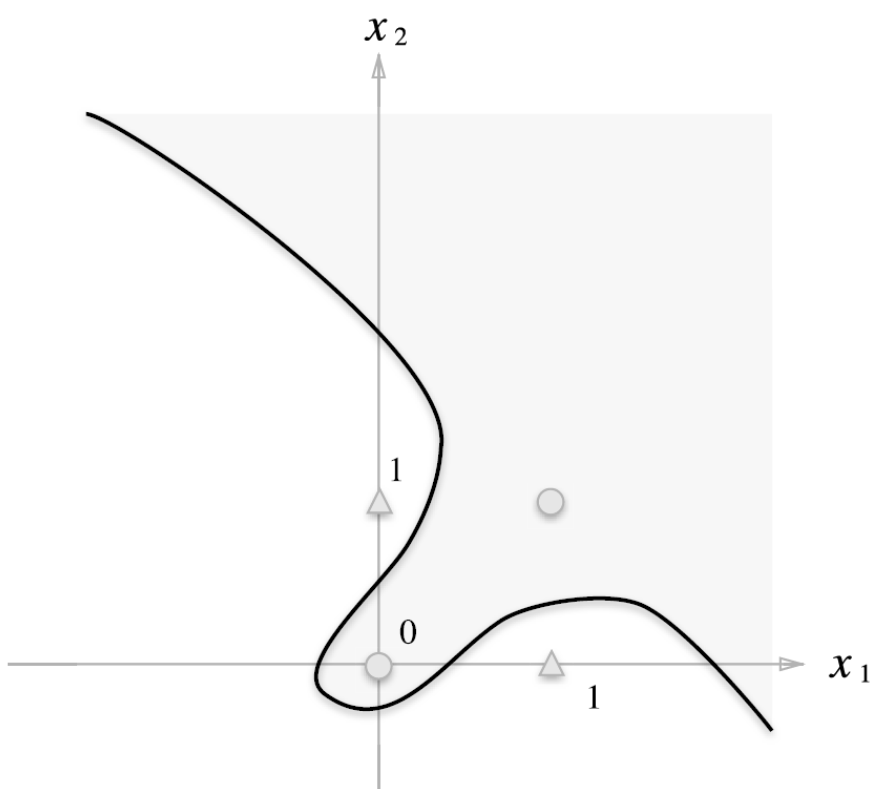
비선형 : XOR 같이 곡선으로 표현할 수 있는 영역
3개의 단순 논리 회로로 XOR (배타적 논리합) 구현 -
XOR 을 구현하고 시각화하면 직선만으로 표현이 안되기 때문에 다층 퍼셉트론(신경망)을 배워보자!
2-4) 다층 퍼셉트론(신경망) : 위 단층 퍼셉트론을 층층이 쌓아 올린 퍼셉트론
-
XOR의 진리표
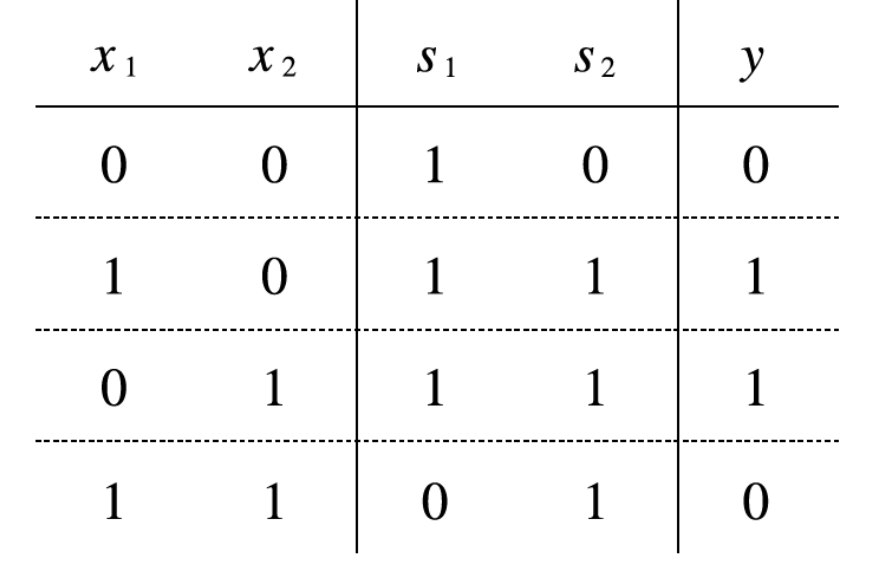
-
XOR의 퍼셉트론
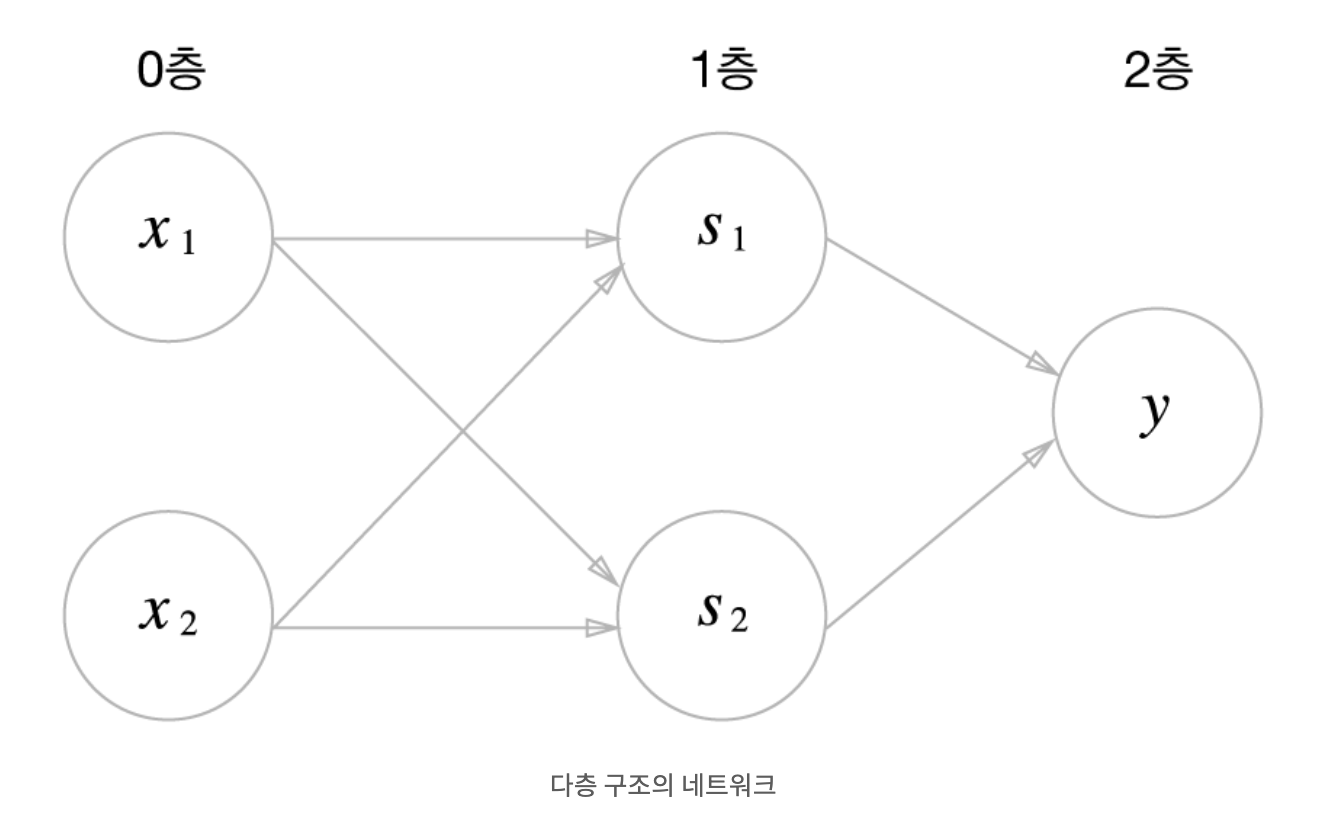
-
1층 S1은 NAND 게이트, S2은 OR 게이트 노드들을 통해 출력된 2개의 값이 2층 AND 게이트를 통하여 XOR 게이트를 구성한다
3. 신경망
- 퍼셉트론 에서 신경망(다층 퍼셉트론) 으로
3-1) 신경망에서 층(Layer)의 구조
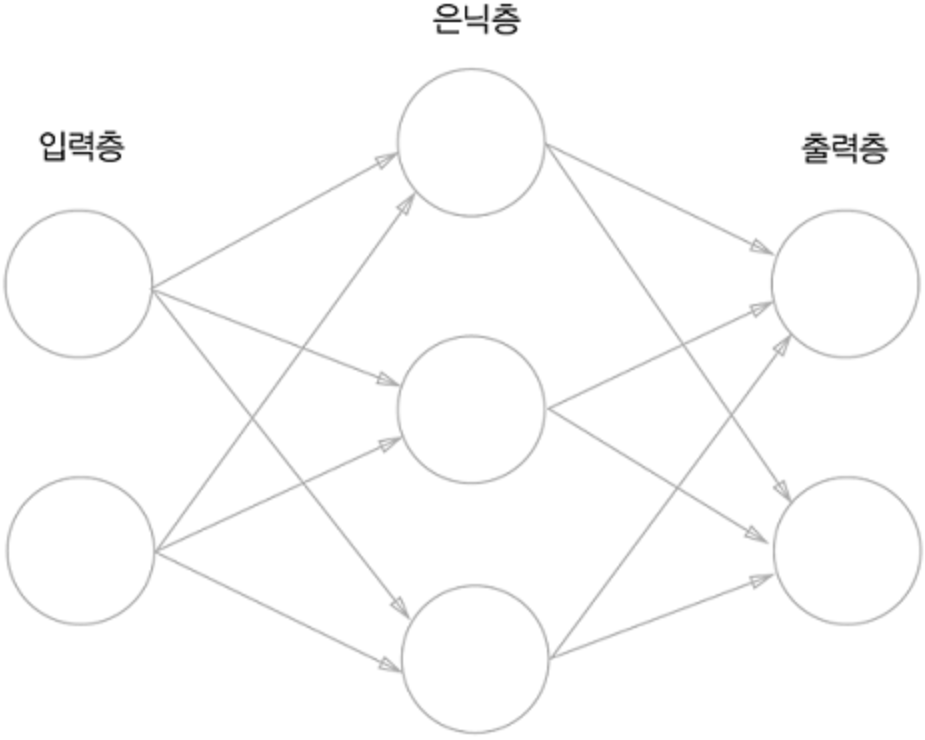
- 입력층 > 은닉층 > 출력층 으로 구성되어 있다
(은닉층을 여러 층 겹겹 쌓으면서 복잡한 신경망을 구성한다)
3-2) 활성화 함수(Activation function)
- 활성화 함수 : 입력 신호의 총합을 출력 신호로 변환하는 함수
1) 활성화를 일으키는지 정하는 역할을 합니다
2) 목적에 맞게 어떤 형태로 출력할 것인지 정하는 역할을 합니다
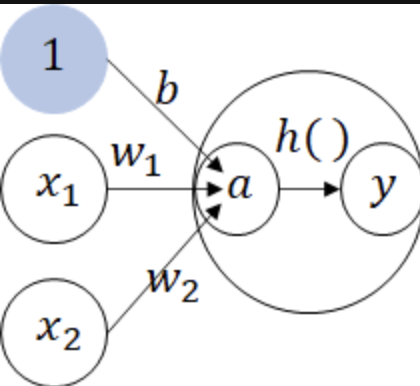
( h( ) 는 활성화 함수이다, 출력노드를 미시적으로 확대해서 표현한 노드 )
3-3) 활성화 함수의 종류
(단층 퍼셉트론에서는 선형 활성화 함수인 계단 함수를 사용했으나 비선형성 도입으로 출력의 표현력을 높게 하기 위해 사용하는 비선형 활성화 함수들의 종류를 설명할 예정 입니다)
0) 계단 함수
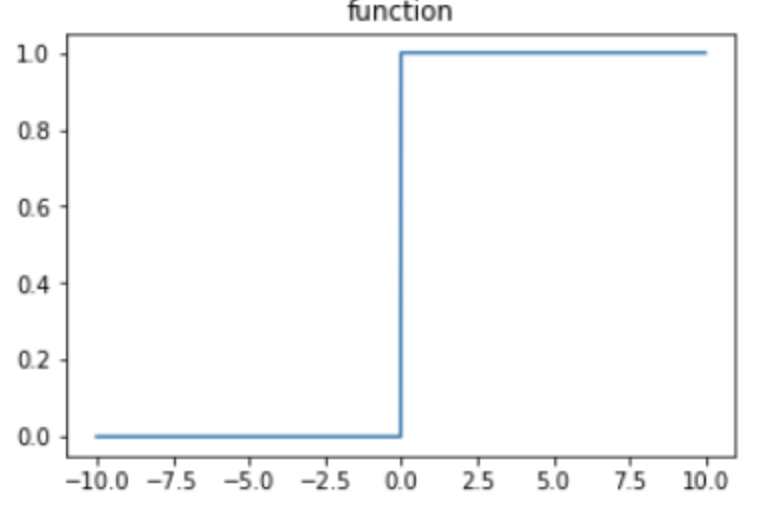
- 특 징
1) 입력 신호를 구간 동안 0,1 값으로 출력
2) x = 0 부분에서 급격한 변화를 갖는다
1) 시그모이드 함수(Sigmoid fucntion)
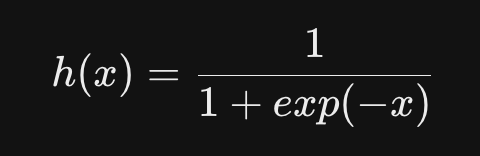
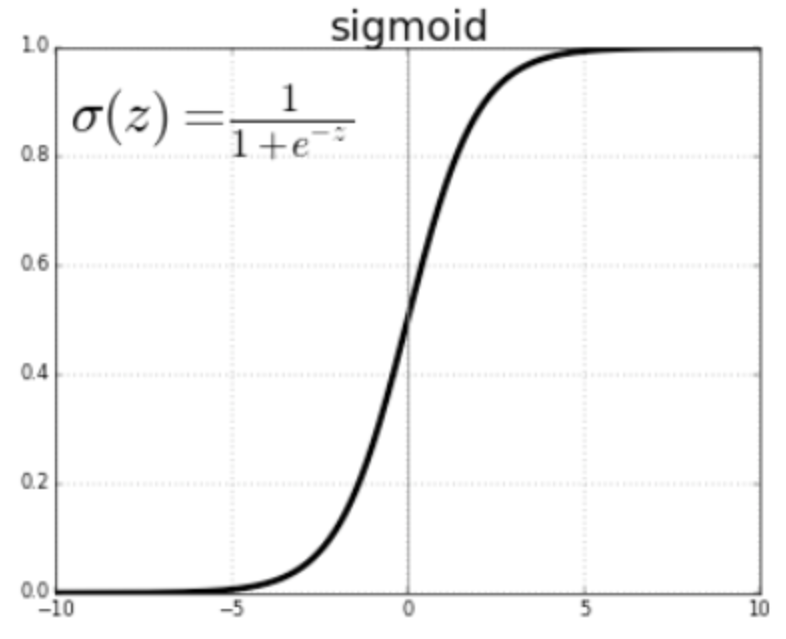
- 특 징
1) 입력신호를 0~1 사이의 연속적인 실수값으로 출력
2) 연속적(매끄러운 곡선)값으로 출력함은 딥러닝에서 중요한 역할을 한다
(출력의 표현력 증가)
2) Relu 함수 (항등함수: 입력값을 출력값으로 그대로 출력하는 함수)
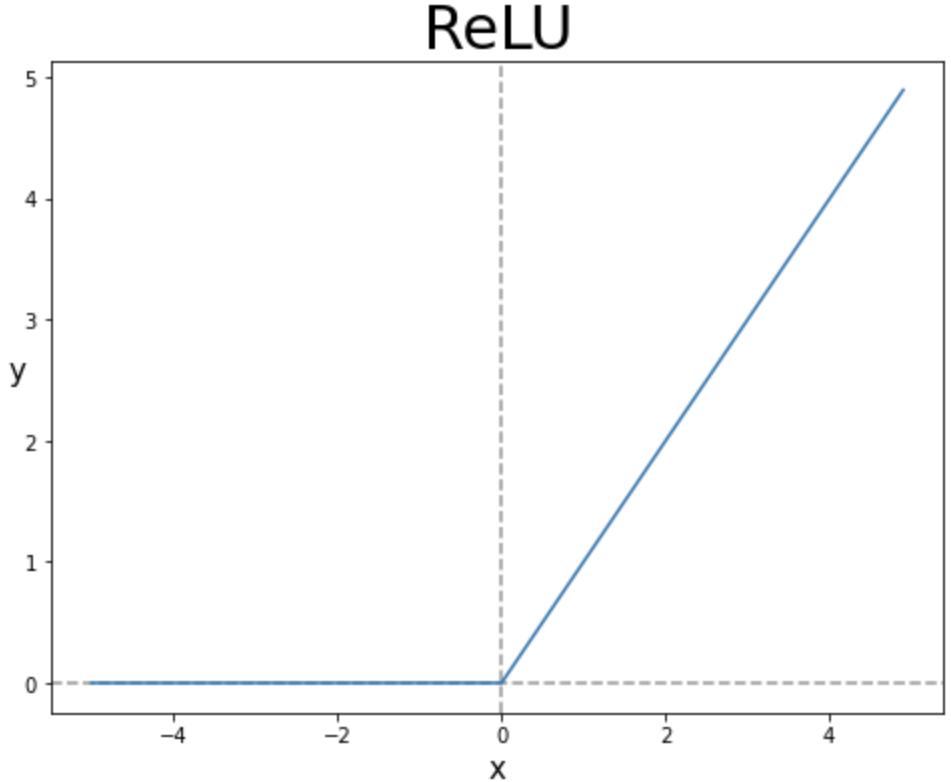
- 특 징
1) 현재는 활성화 함수로 ReLU(Rectified Linear Unit) 함수를 주로 이용합니다
2) ReLU는 입력이 0보다 크면 입력 그대로 출력하고, 0 이하면 0을 출력하는 함수
3) 분류/회귀 문제 중 회귀 문제에 많이 사용 합니다
3-5) 다차원 배열의 계산
1) 다차원 배열
- 다차원 배열은 '숫자들의 집합'으로 구성되어 있다
- 아래 그림은 행렬(matrix)이고 2차원 배열을 행렬이라고 한다. 가로 행(row), 세로 열(colunm)으로 구성되어 있다.
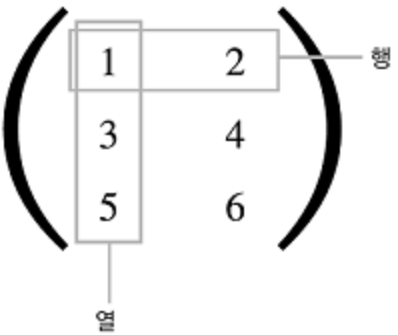
2) 행렬의 내적(행렬의 곱)
- MxN 다차원 행렬곱을 진행할 때 선행 행렬의 N열과 후행 행렬의 M행의 수를 맞춰야 곱이 가능하다 (N1 = M2, 대응하는 차원의 요소 수를 일치시킨다는 의미)
(A = M1 x N1, B = M2 x N2)
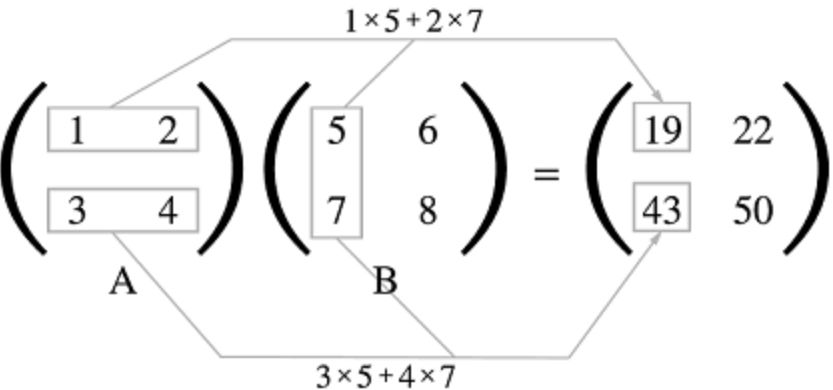
3) 신경망의 내적 (신경망에서 데이터와 가중치들의 수를 다차원 배열로 표현 했을 때의 곱)
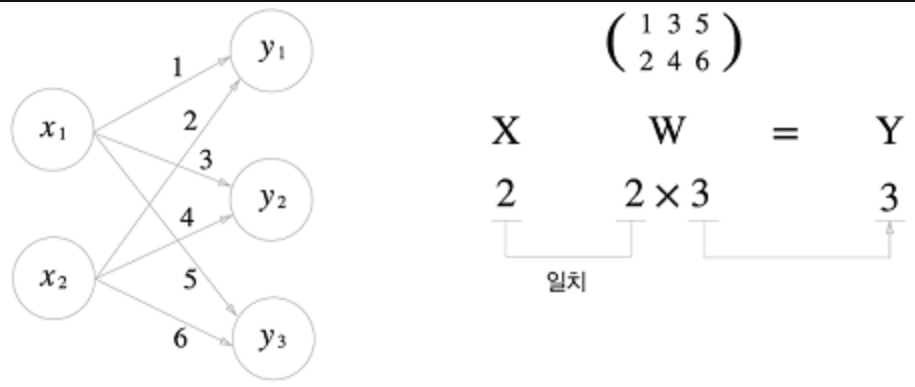
3-6) 3층 신경망 구현하기
1) 각 층의 신호 전달 시각화
-
1층
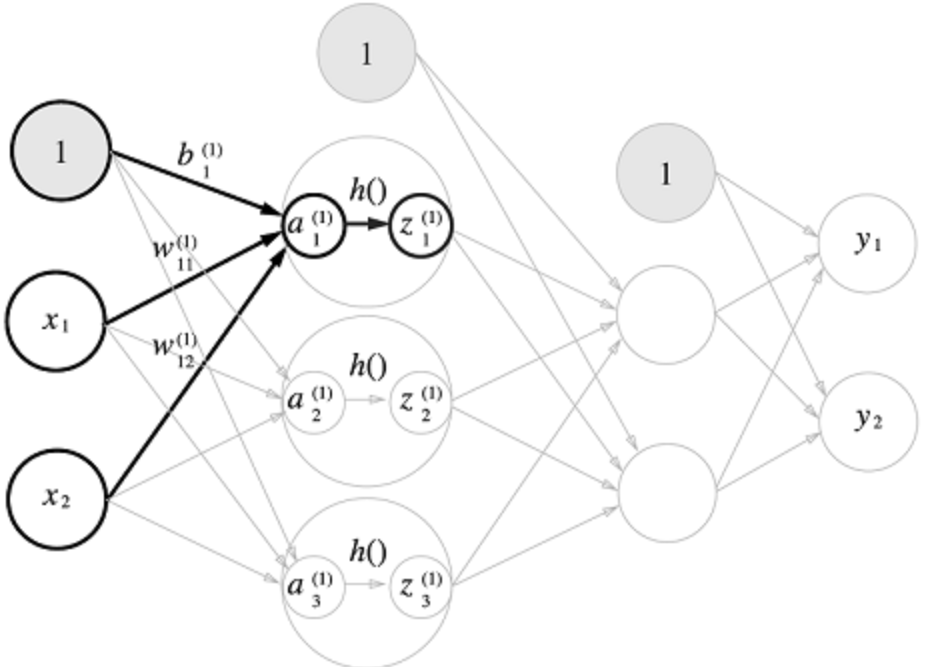
-
2층
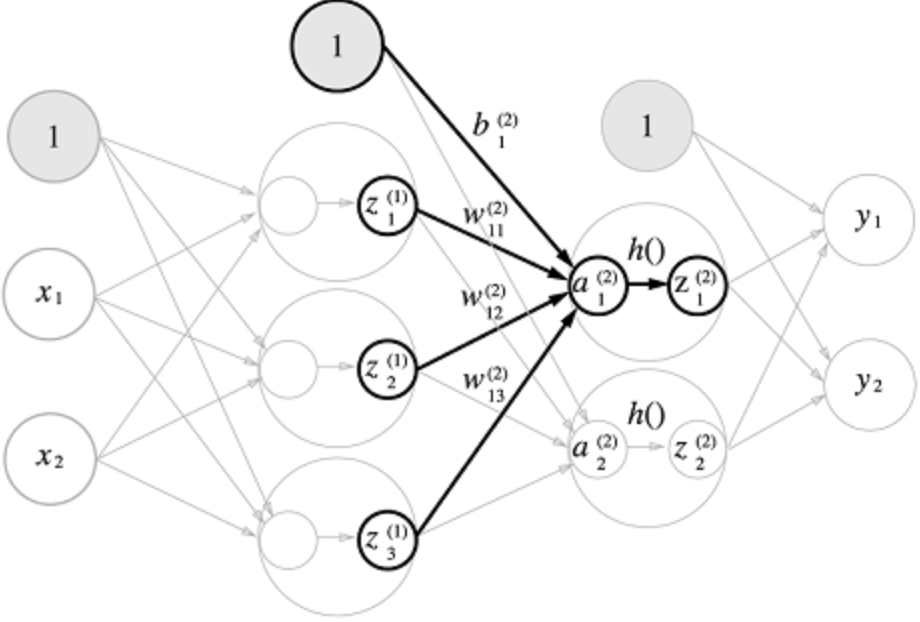
-
3층
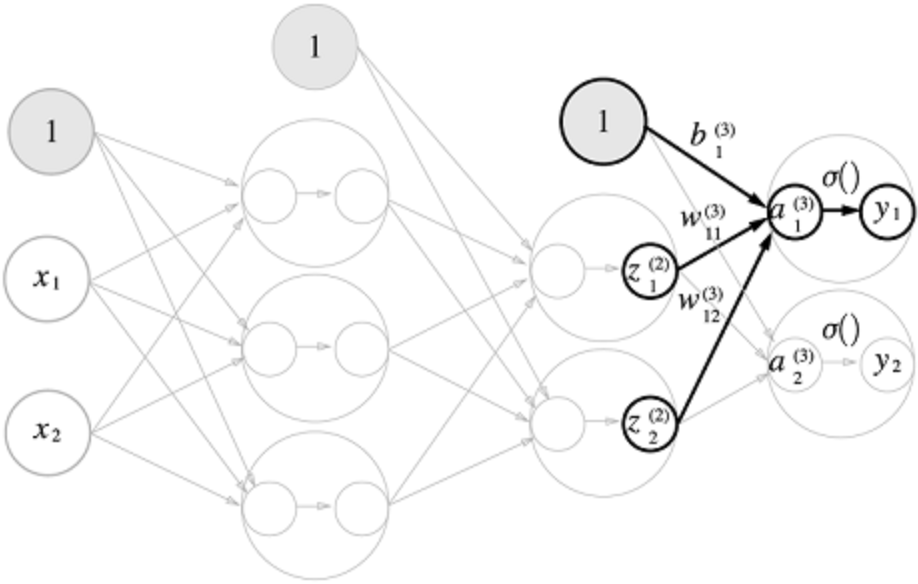
3-7) 출력층 설계하기
- 머신러닝 문제인 분류 & 회귀 두 문제에 모두 이용할 수 있습니다
- 각 문제와 목적에 맞게 활성화 함수를 적용합니다
- 회귀는 항등함수(Relu), 분류는 확률(Softmax) 함수를 사용합니다
1) 회귀에서 항등함수는 입력값 그대로 출력 합니다
2) 분류 문제에서 Softmax 함수 활용
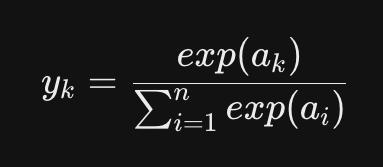
- n은 출력층의 뉴런 수, yk는 뉴런 중 k번째 출력값
- 분자는 ak의 지수 함수(자연상수), 분모는 모든 입력 신호의 지수 함수의 합들로 구성
(출력은 모든 입력 신호로부터 화살표를 받는다. 즉 완전 연결 신경망 이라고 한다. 나중에 설명 나옴!)
2-1) Softmax 함수 구현 시 주의점
-
지수 함수를 사용하는데, 지수 함수는 x축이 커질 수록 y값이 급격하게 증가하기 때문에 오버플로 문제가 발생하여 출력값이 불안정하게 되는 문제가 있습니다.
-
오버플로 문제를 해결하기 위해 원소들 중 최대값을 각 원소에서 빼준다
(아래 지수 함수 특성 상 상수를 연산처리 해도 괜찬다는 증명식)
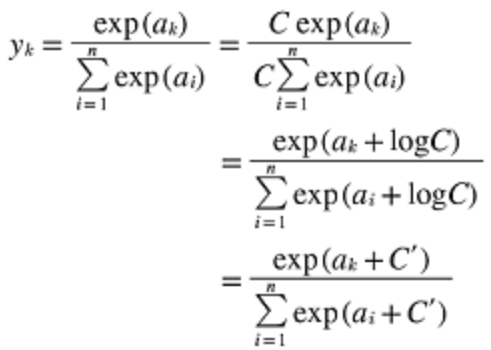
2-2) 소프트맥스 함수의 특징
- 출력의 범위가 0 ~ 1.0 사이의 실수
- 모든 원소들의 합이 1로 확률로 해석이 가능하다
- 추론 과정에서 출력층에서는 소프트맥수 함수를 생략하고 스코어만 출력해도 된다 (비용 절감)
- 지수 함수는 단조 증가 함수이기에, 원소들의 대소 관계는 변하지 않고 출력되기 때문에 출력층에서 생략 가능합니다
- 분류 문제에서의 출력층 뉴런 갯수는 Class에 맞게 설정해야 한다 (뒤에서 Mnist 예제 출력층에서 확인하자!)