Deep.Learngin from Scratch 밑시딥 1권
(1권은 이미지 분류/CV 분야 위주로 구성 되어 있습니다)
(코드적 구현은 따로 작성할 예정 입니다)
(책 내용 그대로 옮기기 보단 저자가 공부하면서 중요한 부분 요약 위주로 작성 했습니다)
목 차
이전 chapter
1. 헬로 파이썬 (생략)
2. 퍼셉트론
- 신경망
현재 chapter
4. 신경망 학습
5. 오차역전파법
6. 학습 관련 기법들
다음 chapter
7. 합성공 신경망(CNN : Convolution Neural Network)
8. 딥러닝
4. 신경망 학습
4-1) 개념
1) 학습 : 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득
2) 손실함수 (Loss function) : 신경망이 학습할 수 있도록 해주는 지표
(감소 시키는 방향)
3) 이미지 분류 학습 방법 : 이미지(데이터)에서 특징(feature) 를 추출하고 특징에서 패턴을 머신러닝이 학습 시킵니다
4) 딥러닝(신경망, end2end) : 단층 퍼셉트론 처럼 사람의 개입 없이 결과를 얻는다
5) 오버피팅(overfitting) : 학습 데이터를 너무 익숙하게 학습한 나머지 새로운 데이터가 input 됐을 때 받아들이지 못하는 상태. (범용 능력을 높여야 한다)
6) 훈련 데이터(train data) : 학습할 때 사용하는 데이터
(최적화 된 매개변수를 찾아가는 것)
7) 시험 데이터(test data) : 범용 능력을 평가하기 위한 데이터 (새로 입력 들어오는 데이터)
8) 원핫 인코딩(one-hot Encoding) : 데이터 피처(colunm)에서 종류마다 0,1로 변환하는 인코딩 방식
4-2) 손실함수의 종류
(출력값을 받아서 Lossfunction에 넣어서 값을 출력 받아 지표로 삼는다)
1) 오차 제곱합 (Sum of Squares for Error, SSE)
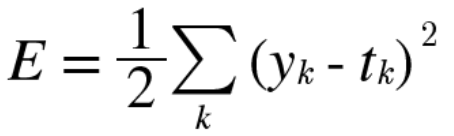
- yk는 예측값(신경망에서 출력값), tk는 정답 레이블, k는 차원 수
- 원-핫 인코딩(Mnist 손글씨 예제에서 0~9 모양의 사진을 분류할 때 10개의 클래스를 0,1로 변환합니다)
(ex. '0'이미지는 배열 [1,0,0,0,0,0,0,0,0,0], '1' 이미지는 배열 [0,1,0,0,0,0,0,0,0,0])
2) 교차 엔트로피 오차 (Cross Entropy Error, CEE)
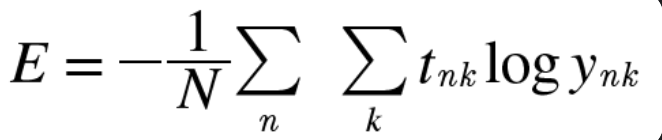
- yk, tk 변수는 위와 동일하고 SSE와 다르게 로그 함수를 활용한다
- x값이 0에 가까울수록 y값은 음의 방향으로 발산하고, 1에 가까울수록 y값은 '0'(오차) 값에 수렴한다
4-3) 미니 배치(batch) 학습
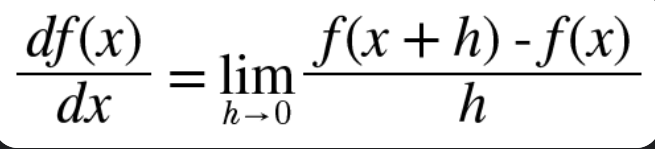
- 데이터 총 개수(N개)로 나눠서 정규화로 '평균 손실 함수'를 구하는 식입니다
미니 배치 학습
총 데이터 개수중 임의의 개수 N개를 묶어서(배치, batch) 학습을 진행하는 방법
4-4) 지표로서 손실 함수를 설정하는 이유
- 정확도(Accuracy)로 지표를 삼아도 되지만 정확도는 연속적인 실수로 매끄럽게 표현할 수가 없기 때문에 손실함수를 설정하며 추후 손실함수의 미분을 통해서 기울기(gradient) 로 최적화 된 매개변수를 찾아가는 방향을 제공 합니다.
(정확도는 지표로 사용하면 미분 시 대부분의 장소에서 미분값이 0이 됩니다)
4-5) 수치 미분
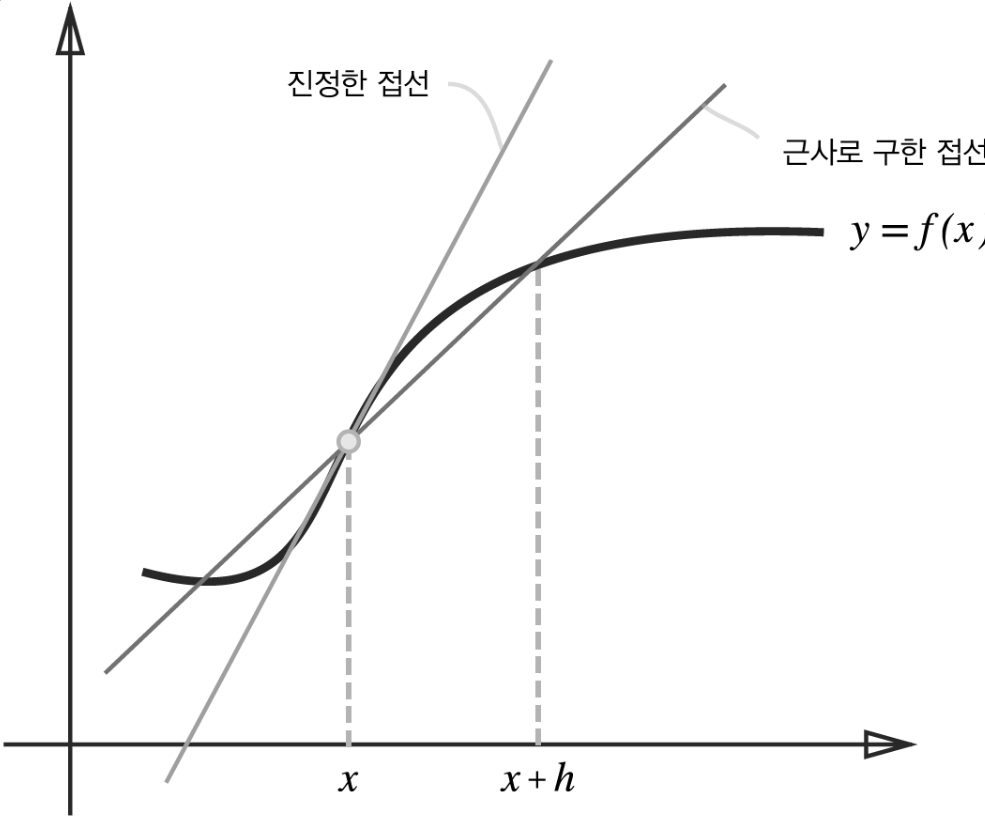
-
차분을 통해 기울기를 구하고 기울기로 최적화 방향을 찾아갑니다
-
차분 : f(x+h)-f(x)의 식으로 x에서 h만큼 떨어진 지점까지의 차이 값
-
미분을 하는 이유는 어느 지점에서의 변화량을 알고자 합니다 (독립변수, 종속변수 개념 구분 중요!)
-
lim를 이용한 극한으로 구하면 좋으나 컴퓨터에선 반올림 오차(rounding error) 로 너무 작은 값은 문제를 일으킵니다. 코드로 구현할 때는 h값을 0에 최대한 가까운 수로 지정해야 합니다
4-6) 편미분
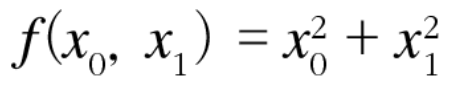
- f(x0, x1) = x0^2 + x1^2 의 식
-
편미분 : 위 식과 같이 독립변수(x, inputdata)가 여러개 일 때 각 독립변수에 대한 종속변수의 미분하는 기법
-
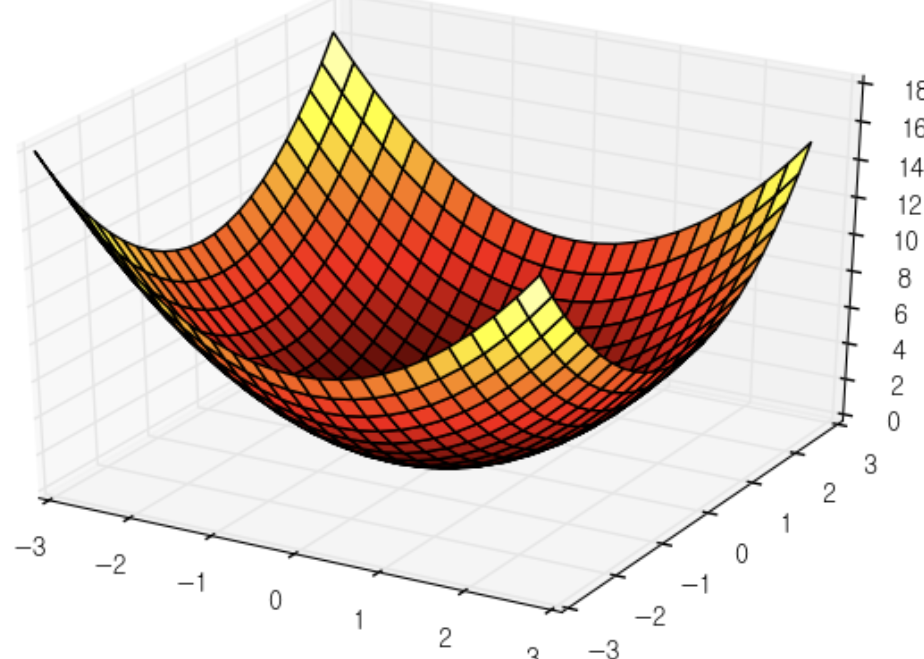
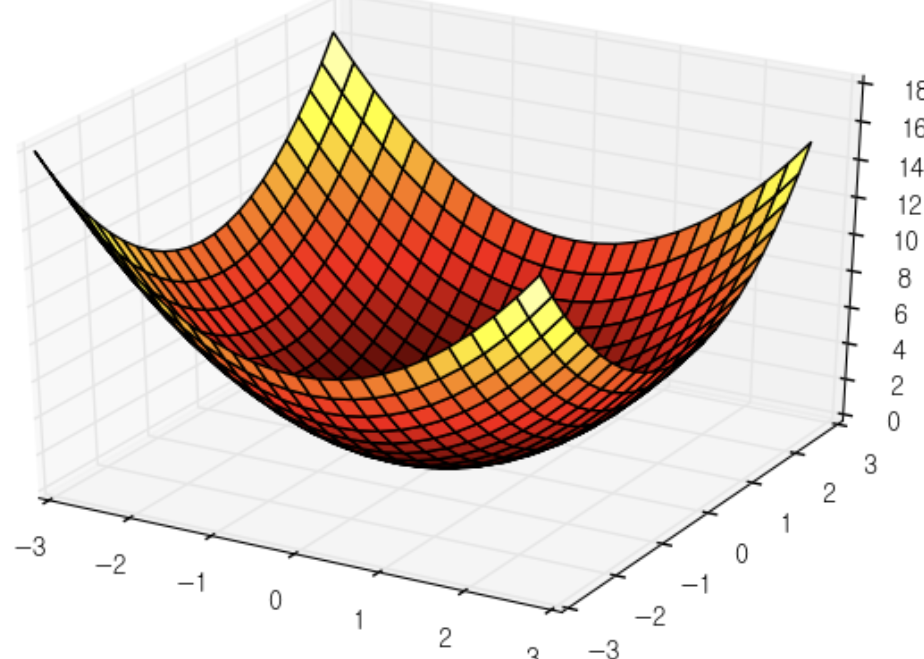
기울기(Gradient) : 모든 독립변수의 편미분을 벡터로 정리한 것을 기울기(gradient, 그레디언트) 라고 한다 (Loss함수의 미분값 즉, 기울기(그레디언트)는 Loss값이 가장 작아지는 방향을 가치켜준다)
<아래 그림에서 추가 설명>
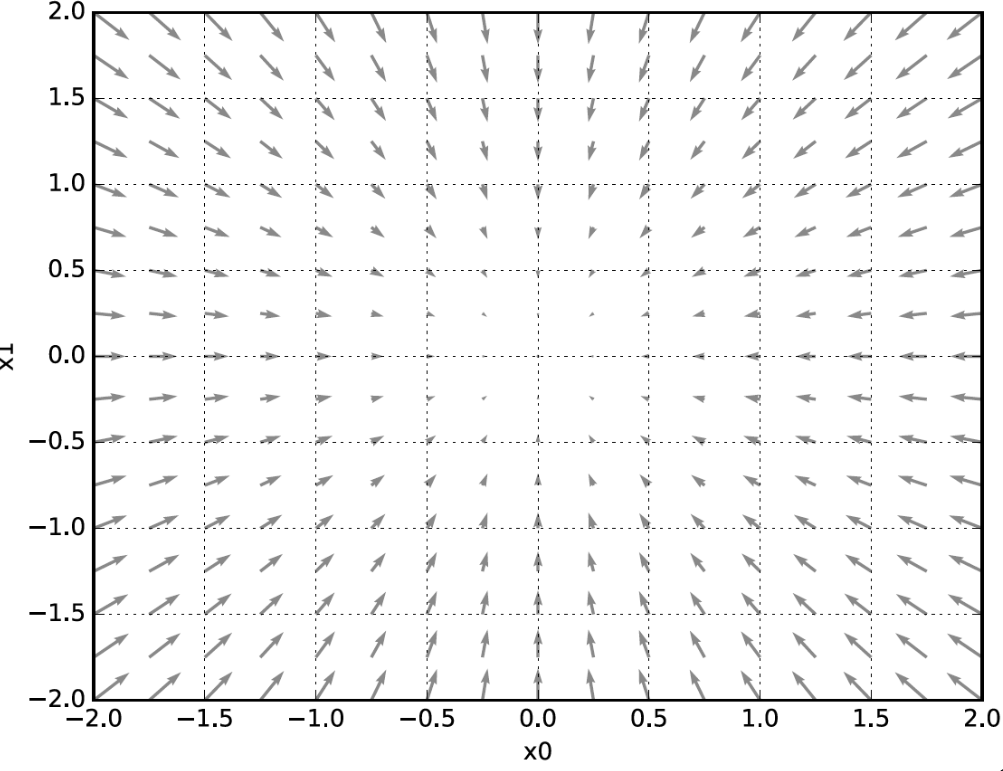
가장 낮은 곳(0,0) 그림의 중심 부분으로 화살표들이 가르키고 있다. 최소값(가장 낮은 곳)에서 먼 곳일 수록 화살표 크기가 크다. 최소값으로 크게 줄인다는 의미이고, 방향은 최소값으로 향해 있다.
4-7) 경사법(경사하강법)
머신러닝 학습에서는 최적의 매개변수(가중치, 편향)를 찾습니다. 딥러닝(신경망)에서도 학습 단계에서 찾아야 합니다. 여기서 최적은 손실함수(Loss function)가 최소값이 될 때의 매개변수 값입니다
-
경사법 : 위 설명의 상황에서 기울기(Gradient)를 활용해서 최솟값을 찾는 방법
(각 지점(x좌표)에서 손실함수의 값을 낮추는 방안을 제시하는 지표가 기울기)
(기울기가 0인 곳이 무조건 최솟값이라고 할 수는 없습니다. 수학적 개념인 안장점, 고원, 극솟값 개념을 확인 해보시면 알 수 있습니다) -
경사하강법 : 경사법 중 최소값을 찾는 방법
(최댓값을 찾는 방법은 경사상승법, 손실 함수의 부호를 반전 시키면 서로 같다)
경사법 수식
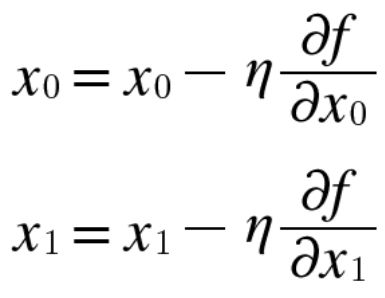
- 위 식 설명
x0 데이터를 이전 x0데이터에서 η(에타, 학습률)과 x0의 미분값(기울기)의 곱을 빼준다
η(에타) : 한 번의 학습(1epoch)로 얼마만큼 학습해야 할지, 즉 매개변수(w,b) 값을 얼마나 갱신하느냐를 정하는 하이퍼파라미터
(w(가중치), b(편향) 같은 매개변수는 학습 시 자동 획득되지만, η(에타,학습률) 같은 하이퍼 파라미터는 사람이 직접 설정해야 합니다)
4-8) 딥러닝(신경망)에서의 기울기
-
행렬을 이용하여 위와 같이 편미분을 통해 기울기(그레디언트)로 행렬에 대응하는 원소(매개변수)들을 갱신합니다. (행x열의 연산 시 특성에 따라 요소의 대응하는 차원을 맞춰줘야 합니다)
-
손실함수를 줄인다는 관점에서 각 행렬 요소들의 미분 값의 양수, 음수 기준으로 반대 방향으로 갱신해 나갑니다. (ex. 미분값 = -0.5h는 양의 방향으로, 0.5h는 음의 방향으로 갱신)
확률적 경사 하강법 (SGD)
간단하고 대표적인 경사 하강법, 미니 배치를 활용하여 무작위로 데이터를 선정해서 갱신하는 방법
(미니 배치(mini batch) : 훈련 데이터 중 일부를 무작위로 가져오는 데이터 묶음, 선별하여 묶은 데이터)
Chapter 4 정리
머신러닝에서 사용하는 데이터 셋은 훈련 데이터(train), 시험 데이터(test) 로 나눠 사용한다
훈련 데이터(train)로 학습하며 모델의 범용 능력(일반성)을 시험 데이터로 사용한다
신경망 학습은 손실 함수를 지표로, 손실 함수의 값이 작아지는 방향으로 가중치 매개변수를 갱신한다
가중치 매개변수를 갱신(updata)할 때는 가중치 매개변수의 기울기를 이용하고 기울어진 방향으로 가중치의 값을 갱신하는 작업을 반복한다
5. 오차역전파(backpropagation)
순전파의 반대 방향으로 연산 하면서 가중치 매개변수의 기울기를 효율적(고속)으로 연산하는 방법
(순전파 과정에서 수치 미분을 사용했지만 단순하고 구허ㅕㄴ은 쉽지만 연산이 오래 걸립니다)
오차역전파는 수식 or 계산 그래프로 표현할 수 있습니다. 여기서는 계산 그래프를 활용 합니다
(수식은 수학적으로 정확하고 간결, 계산 그래프는 시각화로 직관적이게 표현)
- 스탠포드 대학의 CS231n을 참고 하시면 더욱 좋습니다
5-1) 순전파 계산 그래프
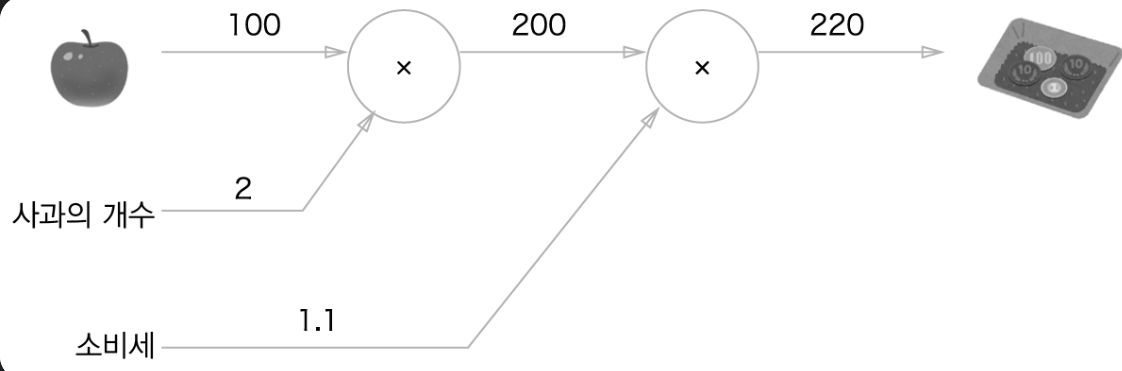
100원 짜리 사과의 10% 소비세의 대한 순전파 그래프 입니다. 사과의 개수와 소비세 2개의 변수로 취급해서
노드 밖에 표기 합니다. 계산 진행 방향은 왼쪽에서 오른쪽으로 진행 합니다
위 과정의 반대로 진행하는 것이 오차역전파(backpropagation) 이라 합니다. 역전파 라고 부릅니다
국소적 계산
국소적 계산 : 자신과 직접 관계된 작은 범위, 각 노드에서의 자신과 관련한 계산
(이 개념은 뒤에 역전파에서 각 노드에서 그 노드만의 미분값을 국소적으로 계산해서 전달하기 때문에 설명)
(각 독립변수에 대한 y의 미분값 전달)
5-2) 연쇄 법칙 (Chain Rule)
위에 설명한 국소적 계산을 순전파(왼>오른)의 방향에 반대로 역전파(오른>왼)를 진행 할때 전달하는 원리를 연쇄 법칙 이라고 합니다
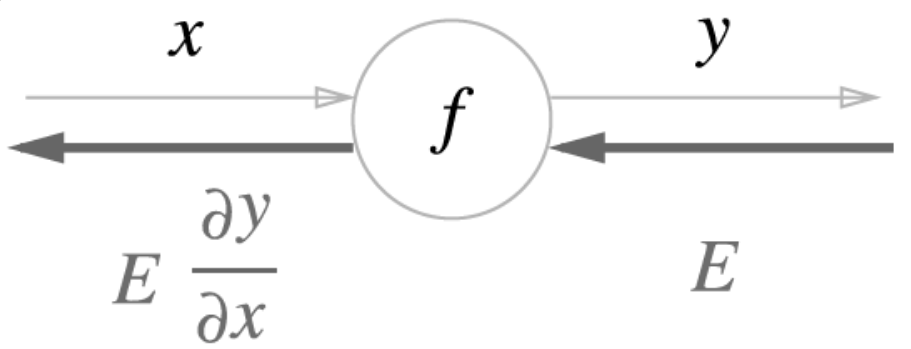
연쇄 법칙이란? (함수적 수식으로 표현)
합성함수 : 여러 함수들이 구성되어 있는 함수
연쇄법칙의 원리 : 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다
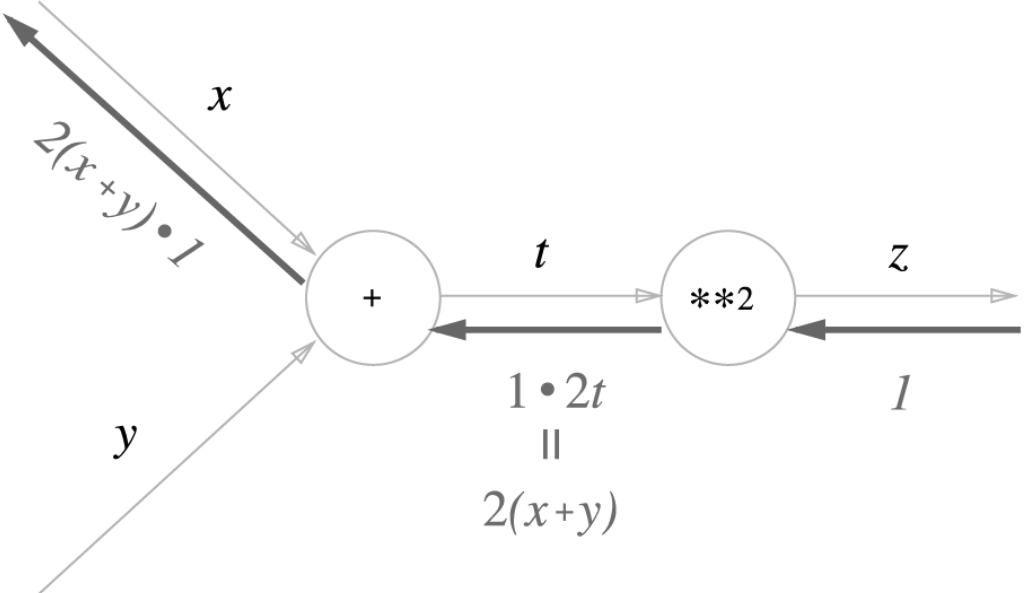
<연쇄 법칙을 사용한 예제>
1) 2개의 함수로 구성된 합성 함수
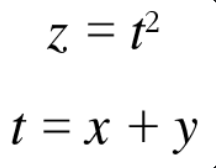
2) x에 대한 z의 미분 = (t에 대한 z의 미분) x (x에 대한 t의 미분)
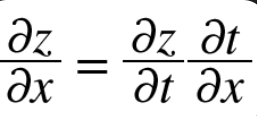
3) 각각 미분 했을 때의 식
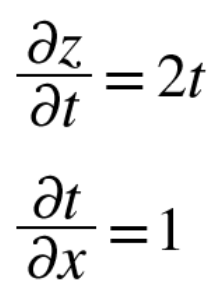
4) 2번 식에 3번 식을 대입 했을 때 최종 연쇄 법칙을 통한 식
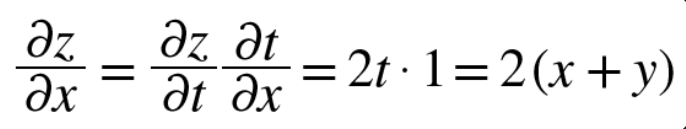
5-3) 연쇄법칙과 계산 그래프
<위 예제 식 참조>
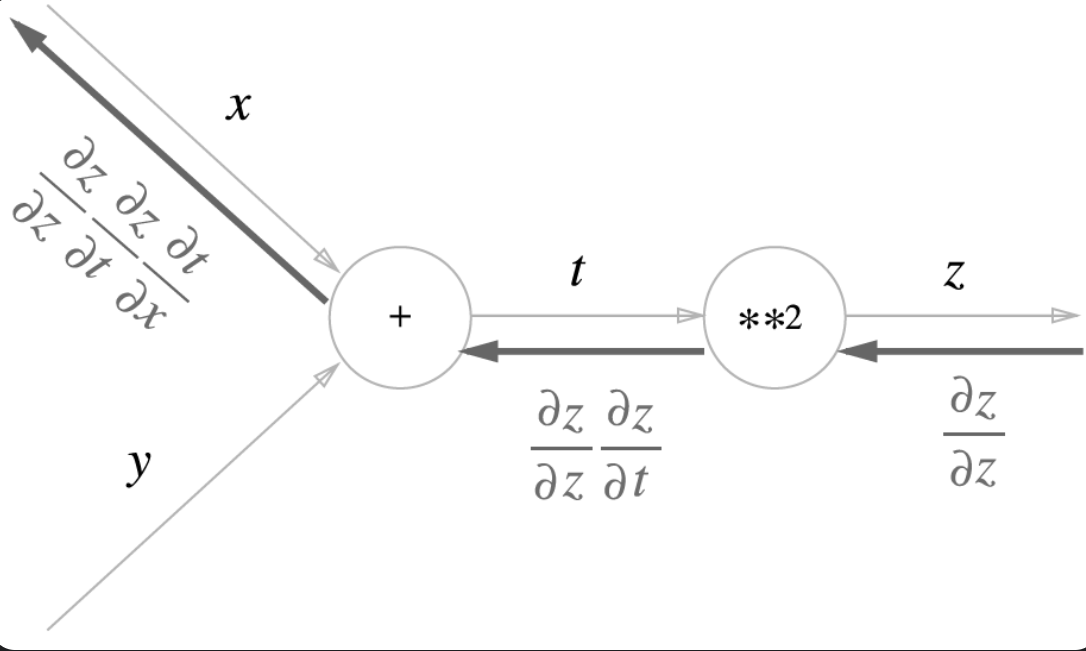
역전파의 계산 방향에서는 노드로 들어온 입력 신호에 해당 노드의 국소적으로 미분(편미분)을 곱하고 다음 노드로 전달된다. 역전파가 전달되늰 원리는 연쇄 법칙 이다
아래는 계산 그래프에 예제 식을 대입
5-4) 역전파의 구조
구분에 맞게 어떻게 input, output 되는 값과 방향만 정리 했습니다
자세한 수식과 과정은 책 참조 해주세요 (더 자세하게는 부록 294p 참조!)
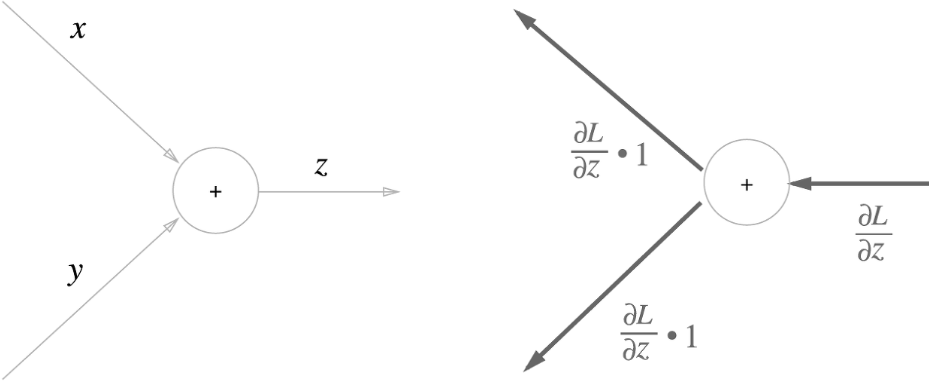
- 덧셈 노드의 역전파 ( ' + ' )
노드 기준으로 입력된 미분값에 '1'이 곱해져서 입력 미분값 그대로 다음 노드로 출력한다
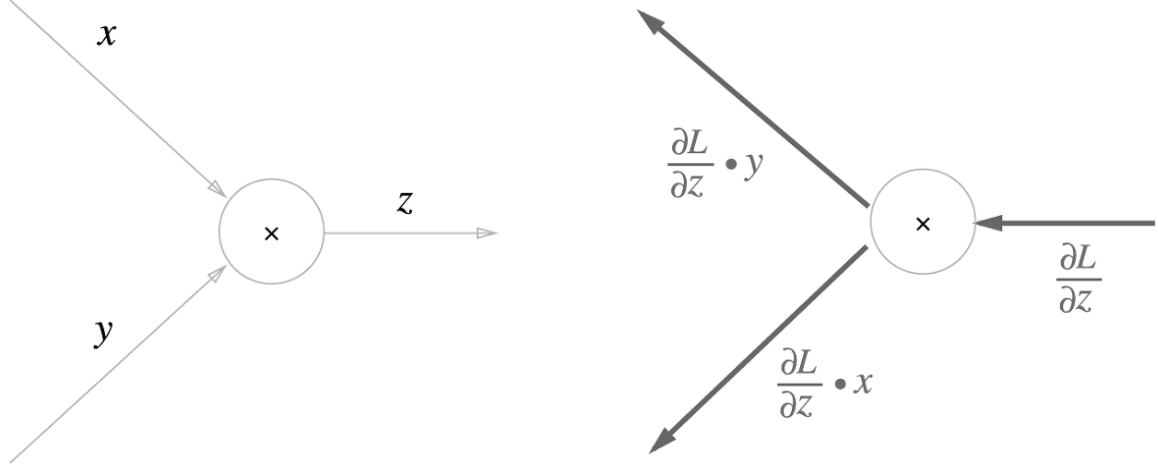
- 곱셈 노드의 역전파 ( ' x ' )
곱셈 노드 역전파는 상류의 값에 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해서 하류로 보냅니다
풀이) 방향은 노드 기준, y의 역전파(출력방향) = z의 역전파(입력방향) x input x 순전파(입력방향)
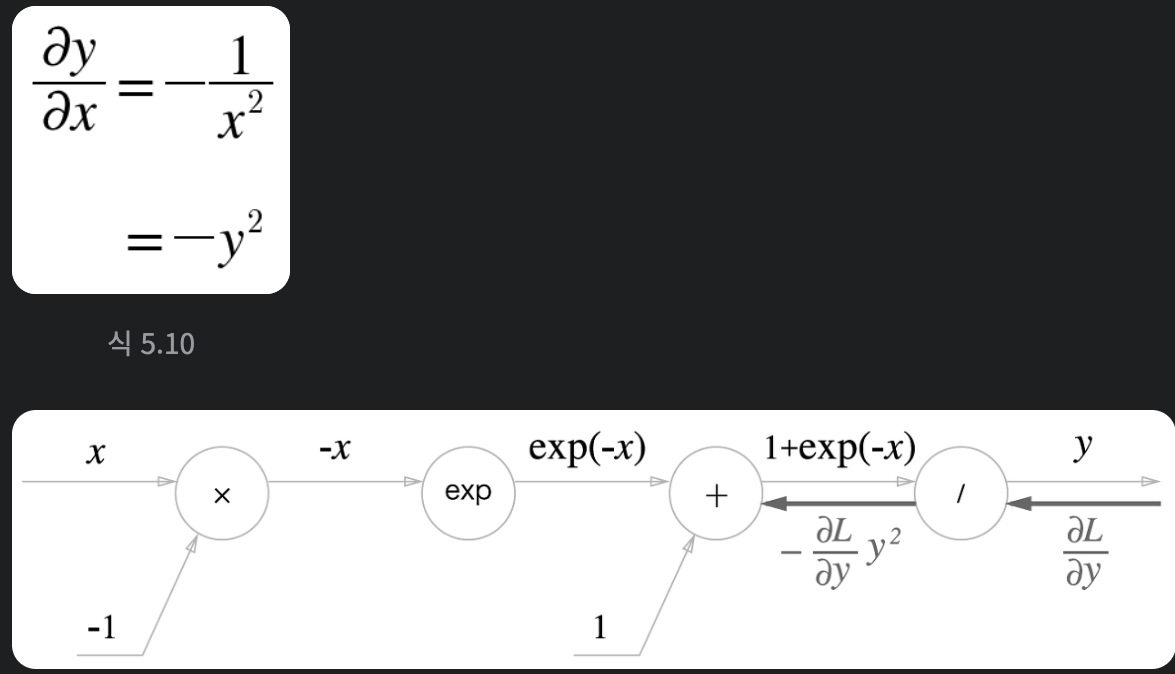
- 활성화 함수(Sigmoid) 계층에서 연산 노드의 역전파( ' / ' & ' exp ' )
- ' / ' 나누기 노드
역전파 때 상류에서 흘러온 값에 -y^2(순전파의 출력을 제곱한 후 마이너스를 붙인 값)을 곱해서 하류로 전달합니다
풀이) 방향은 노드 기준, '/'노드 출력 역전파 = (상류에서 흘러온 역전파) x -(나누기 노드에서 순전파 때 출력값)^2
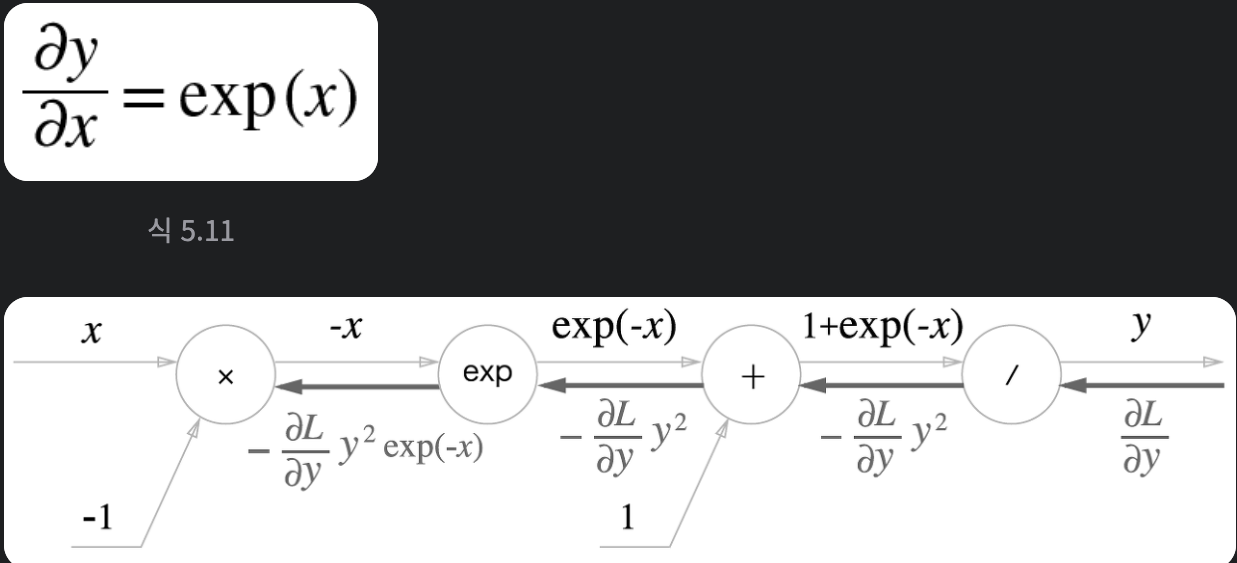
' / ' 노드와 ' exp ' 노드는 꼭 부록 참고!
- ' exp ' e(자연상수)의 지수 노드
상류의 값에 순전파 때의 출력(예시에서는 exp(-x))을 곱해 하류로 전달 합니다
풀이) 방향은 노드 기준, 'exp'노드 출력 역전파 = (입력 역전파들의 합) x exp(x) (부록)
5-5) Affine 계층
순전파 때 수행하는 행렬의 곱은 기하학에서는 어파인 변환(Affine transformation) 이라 한다.
Affine 계층은 선형 변환이다!(중요) 활성화 함수를 통해 비선형성이 도입 되는 점 기억해두자!
Chapter 5 정리
계산 그래프를 이용하면 계산 과정을 시각적으로 파악할 수 있다
계산 그래프의 노드는 국소적 계산으로 구성되며 국소적 계산을 조합해 전체 계산으로 구성한다
계산 그래프의 순전파는 통상의 계산을 수행한다. 계산 그래프의 역전파로는 각 노드의 미분을 구할 수 있다
신경망의 구성 요소를 계층으로 구현하여 기울기를 효율적으로 계산할 수 있다(오차역전파법)
수치 미분과 오차역전파법의 결과를 비교하면 오차역전파법의 구현에 잘못이 없는지 확인할 수 있다
(역전파로 빠르게 최적 매개변수를 갱신하고, 순전파(수치 미분)와 비교하여 역전파 구현에 문제점 확인 가능하다(기울기))