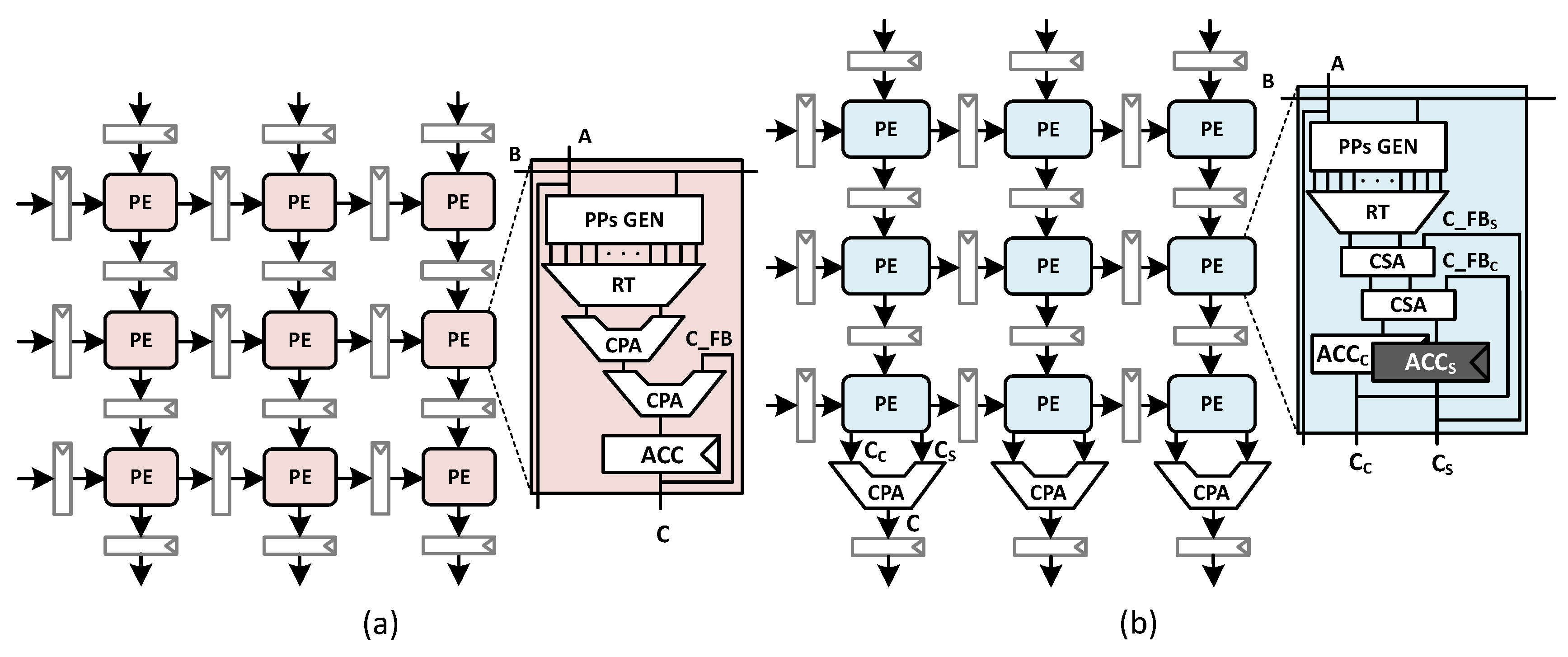
일단 기존의 CNN 가속기 아키텍처 2가지를 알아보자
각각 systolic array 방식과 adder tree 방식인데 먼저 systolic array 방식부터 알아보자
Inayat K, Chung J. Carry-Propagation-Adder-Factored Gemmini Systolic Array for Machine Learning Acceleration. Electronics. 2021; 10(6):652. https://doi.org/10.3390/electronics10060652
위 그림에서 (a) 그림이 systolic array 방식이다. (b)는 이를 조금 변형한건데 오늘 다룰 내용과는 상관없으니 무시해도 좋고 내부 PE 구조는 어떻게 설계하느냐에 따라 다르니 그에 대한 내용도 무시해도 좋다.
systolic array는 곱셈과 덧셈을 수행하는 PE와 D-Flip Flop(이하 FF)이 의도에 맞게 배치되어 있는 형태다. 그림의 경우 2D로 배치되어 있다.
왼쪽에서는 input, 즉 이미지에서 각 픽셀의 데이터등이 입력되고 해당 데이터들은 PE에 할당되며 동시에 오른쪽의 FF로도 전달된다.
즉 입력된 데이터는 사이클마다 오른쪽의 PE로 이동해 입력된다는 뜻이다.
예를 들어서 3개의 PE와 그에 맞게 FF가 배치되었을 때 1,2,3의 데이터를 차례로 입력한다면
(1,x,x) -> (2,1,x) -> (3,2,1) 식으로 input이 PE에 입력되는 것이다.
FF은 수평으로만이 아니라 수직으로도 배치되어 있는데 이는 PE에서의 계산결과를 밑으로 보내기 위함이다.
즉 각 PE의 계산결과는 매 사이클마다 밑의 PE로 보내져 밑의 PE는 input과 weight의 곱셈값에 이를 더하고 결과로 출력한다.
같은 systolic array 방식이라도 어떻게 값을 배치하느냐에 따라 데이터의 흐름에 약간의 차이가 있는데 결국 근본적인 방식은 변하지 않는다. 한가지 예를 들어 설명해보자.
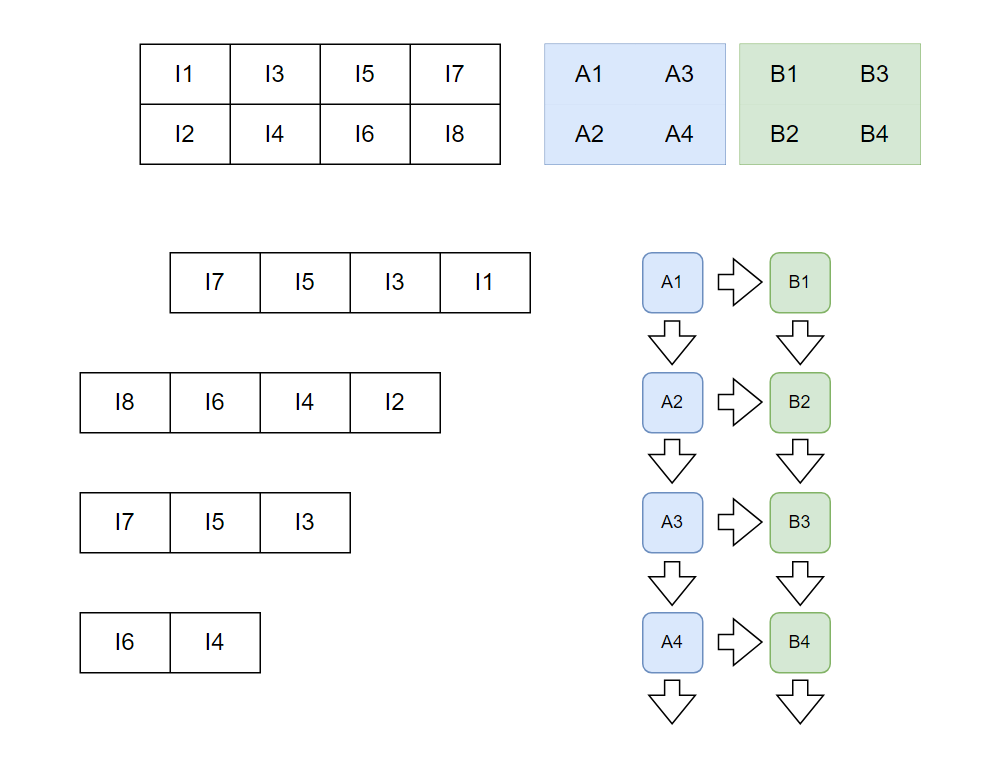
2개의 필터에 대해 컨볼루션 연산을 하는 과정인데 파란색과 초록색인 2개의 필터가 같은 input에 대해 컨볼루션을 한다.
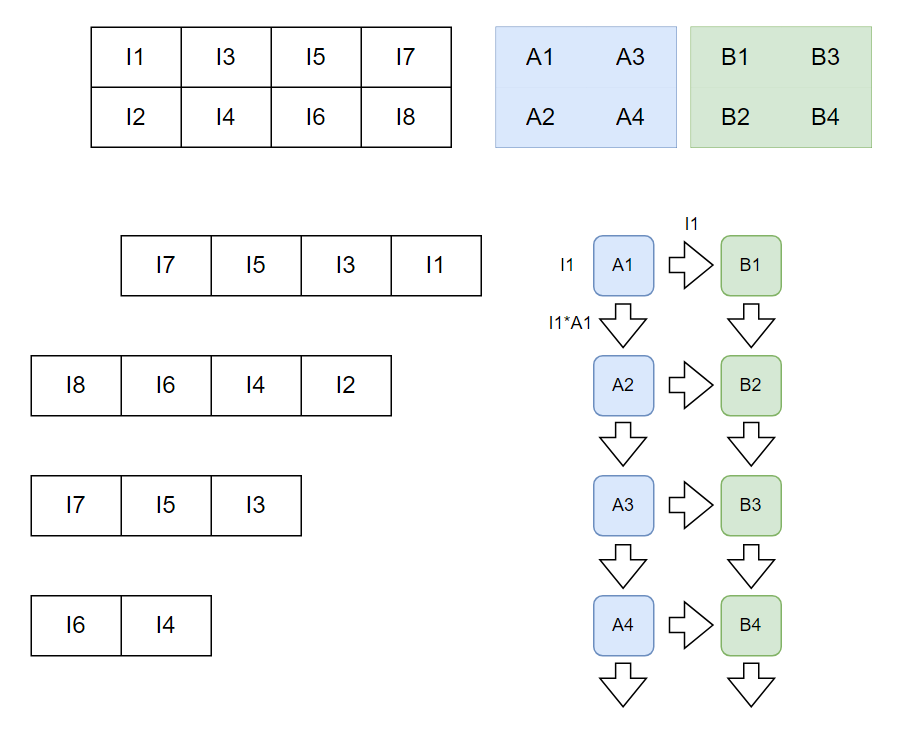
첫 사이클에서 weight A1이 입력된 PE에 input I1이 입력되면 I1을 오른쪽 FF에, I1*A1을 아래쪽 레지스터에 저장한다.
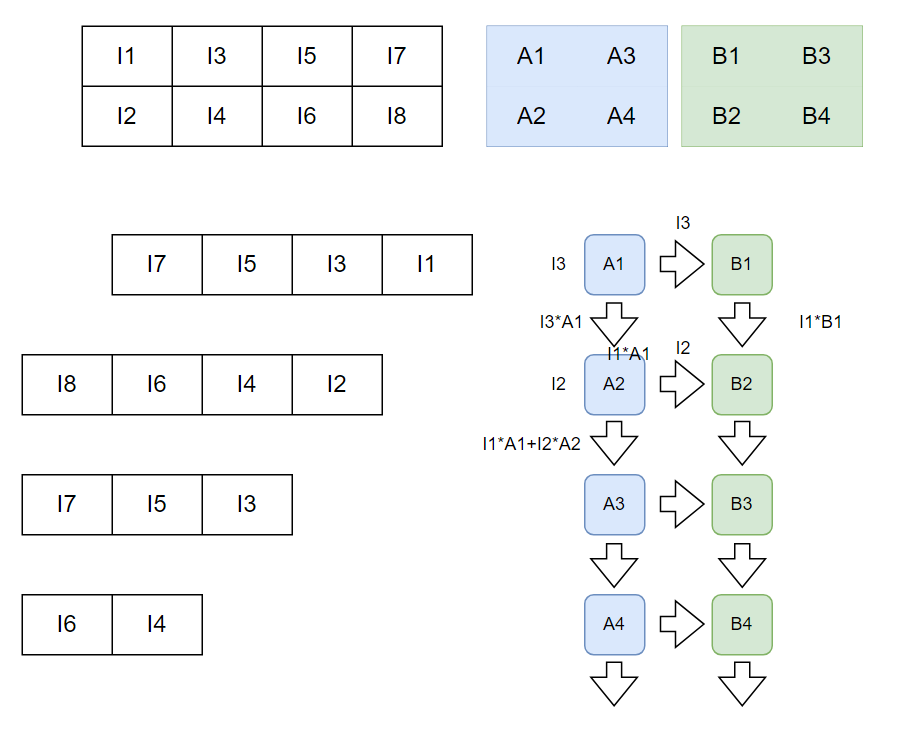
두번째 사이클에서 A2 weight가 입력된 PE는 입력된 input에 대해 I2*A2를 계산한 후 위의 PE에서 전 사이클에 계산되어 전달된 I1*A1을 더해 I1*A1 + I2*A2를 아래 레지스터에 전달한다.
이러한 과정을 거치다보면 파란색 필터는 5사이클부터 초록색은 6사이클부터 매 사이클마다 유효한 값이 출력된다.
더 많은 필터를 계산하고 싶으면 행을 늘리면 되고 더 많은 weight를 가진 필터를 계산하고 싶으면 열을 늘리면 된다.
또다른 방식인 adder tree 방식은 매우 간단하다.
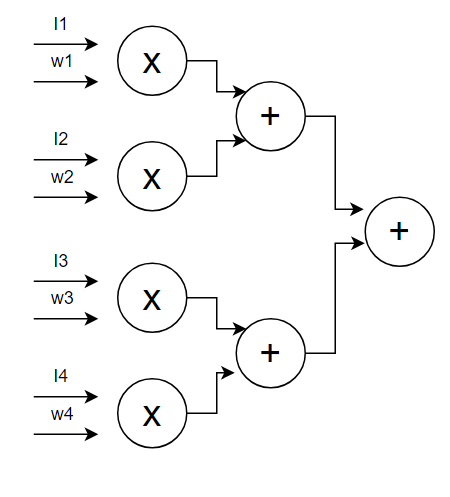
각 곱셈기에 알맞게 input과 weight을 입력한 후 계산값을 덧셈해서 출력하면 된다.
더 많은 weight 개수를 가진 필터를 계산하려면 곱셈기를 더 많이 배치하고 더 많은 필터를 계산하고 싶으면 adder tree를 여러개 배치하면 된다.
두가지 방법을 소개했는데 장단점은 굳이 설명하지 않았다. 사실 내부 구조에 따라 천차만별이기 때문이다.
다만 어느 쪽이건 범용성이 부족한데 필터의 weight 개수에 크게 영향을 받는다는 것이 치명적이다.
만약 systolic array가 9개의 행을 갖는다면 해당 systolic array는 4*4 필터를 계산할 수 없다.
마찬가지로 adder tree도 9개의 곱셈기를 가진다면 16개의 weight를 갖는 4*4 필터를 계산할 수 없다.
그렇다고 16개행, 16개 곱셈기를 배치한다면 반대로 3*3 필터를 계산할 때 많은 부분이 낭비된다.
이러한 단점을 계산하기 위해 나는 input의 크기, weight의 개수 등 여러가지 convolution에 대해서 어느 정도 효율적인 계산이 가능한 아키텍처를 구상했다.