데이터를 학습용과 테스트용으로 나누기
# Train/Test Split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)
# x => 입력 데이터
# Y => 출력 데이터
# test_size => 테스트 데이터 비율
# shuffle => 데이터를 섞을지 여부(기본은 True)
trainsets = TensorData(X_train, Y_train)
trainloader = DataLoader(trainsets, batch_size=32, shuffle=True)
testsets = TensorData(X_test, Y_test)
testloader = DataLoader(testsets, batch_size=32, shuffle=False)
- train_test_split 함수는 데이터를 무작위로 섞어 학습용과 테스트용으로 나눈다.
- test_size는 전체 데이터의 50%를 테스트 데이터로 사용한다는 의미.
- 학습용 데이터는 모델을 학습 시키는 데에 사용되고, 테스트용 데이터는 학습한 모델이 얼마나 잘 동작하는지 평가하는 데 사용한다.
- TensorData를 이용해서 PyTorch가 처리할 수 있는 텐서 형태로 변환한다.
- DataLoader를 사용해 데이터를 배치 단위로 나누고, 학습 시에는 데이터를 무작위로 섞는다.
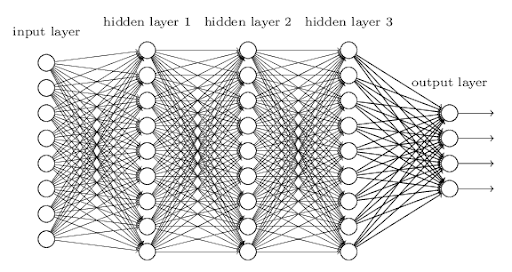
MLP 모델의 정의
class Regressor(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(13, 50) # 입력층(13개 특징값) -> 첫 번째 은닉층(50개 노드)
self.fc2 = nn.Linear(50, 30) # 첫 번째 은닉층 -> 두 번째 은닉층(30개 노드)
self.fc3 = nn.Linear(30, 1) # 두 번째 은닉층 -> 출력층(1개 값: 집값)
self.dropout = nn.Dropout(0.2) # 과적합 방지를 위한 드롭아웃(20%)
def forward(self, x): # 모델의 연산 순서 정의
x = F.relu(self.fc1(x)) # 첫 번째 레이어 + 활성화 함수(ReLU)
x = self.dropout(F.relu(self.fc2(x))) # 두 번째 레이어 + 드롭아웃 + ReLU
x = F.relu(self.fc3(x)) # 마지막 레이어 + ReLU
return x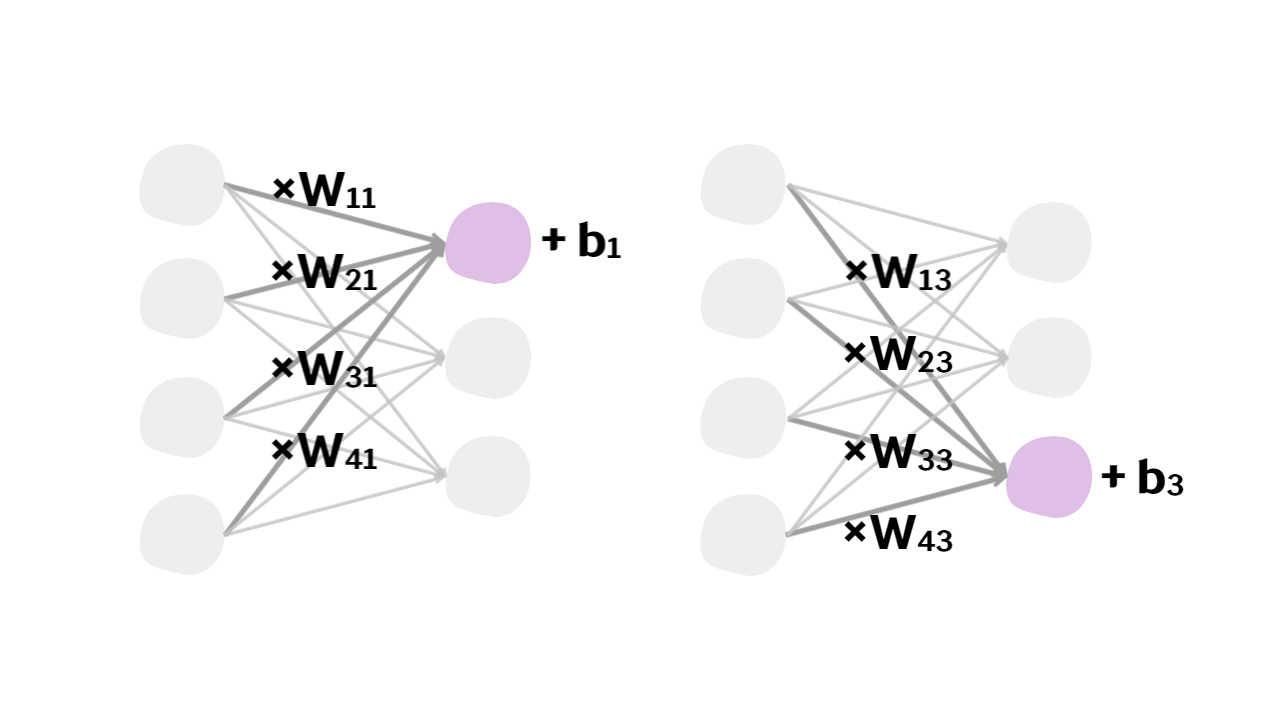
모델 구조
입력층: 13개 입력.
첫 번째 은닉층: fc1 (13→50) → ReLU.
두 번째 은닉층: fc2 (50→30) → ReLU → Dropout(0.2).
출력층: fc3 (30→1) → ReLU.
+Dropout: 과적합 방지를 위해 학습 중 노드의 20%를 랜덤으로 제외.
학습의 흐름:
입력 데이터를 선형 변환 및 활성화 함수 적용.
은닉층에서 특징 학습.
드롭아웃으로 과적합 방지.
최종 예측값 출력.
Z = XW + b
X: 입력 데이터(배치 크기N x 입력 노드 개수)
W: 가중치 행렬(입력 노드 개수 x 출력 노드 개수)
b: 바이어스 벡터(1 x 출력 노드 개수)
Z: 선형 변환의 결과(배치 크기 N x 출력 노드 개수)
ex)
x = F.relu(self.fc1(x)) # fc1: nn.Linear(13, 50)
입력값 크기:
x는 (N×13) 크기의 행렬입니다.
여기서 N은 배치 크기(한 번에 처리할 샘플 수)를 의미합니다.가중치 행렬:
W1 은 (13×50) 크기의 행렬입니다.
입력 노드 13개와 출력 노드 50개를 연결하는 가중치를 포함합니다.행렬 곱 연산:
- Z = XW + b
여기서 Z는 (N×50) 크기를 갖습니다.
이는 입력 데이터를 가중치와 곱하고 바이어스를 더한 결과입니다.ReLU 적용:
- A = ReLU(z)
ReLU 함수는 z 의 음수 값을 0으로 변환하고, 양수 값은 그대로 유지합니다.
손실 함수와 최적화 함수 정의
model = Regressor() # 모델 초기화
criterion = nn.MSELoss() # 손실 함수: 평균 제곱 오차 (MSE)
optimizer = optim.Adam(model.parameters(), lr=1e-2, weight_decay=1e-7)#(weight/bias반환 파라미터, 학습률(0.01), 정규화)
model = Regressor()
손실 함수는 모델이 얼마나 잘 예측했는지, 또는 얼마나 틀렸는지를 측정하는 기준이다.
여기서 사용하는 nn.MSELoss는 평균 제곱 오차(MSE)를 계산한다
- MSE는 예측값과 실제값의 차이를 제곱한 값의 평균으로 구한다.
- 제곱을 사용하기 때문에 차이가 클수록 손실 값이 크게 증가하여, 큰 오차를 더 강조한다.
최적화 함수는 손실 값을 줄이기 위해 모델의 가중치(weight)와 바이어스(bias)를 업데이트하는 역할을 한다.
Adam
- Adam 최적화 알고리즘의 특징
Adam은 SGD(확률적 경사 하강법)을 개선한 방법으로, 학습 속도와 안정성이 뛰어나다.
각 파라미터마다 적응형 학습률을 계산하여 업데이트를 수행한다.요약
- 모델이 데이터를 학습하며 예측을 수행한다.
- 손실 함수가 예측값과 실제값의 차이를 계산하여 손실 값을 반환한다.
- 최적화 함수가 손실 값에 따라 가중치와 바이어스를 조정한다.
- 이 과정이 반복되면서 모델이 점점 더 정확한 예측을 하도록 학습한다.
모델 학습
ep = 0 # 가장 낮은 손실을 기록한 에포크를 저장할 변수
ls = 1 # 초기 손실 값, 비교 기준이 될 매우 높은 값으로 설정
loss_ = [] # 손실 값을 저장할 리스트
n = len(trainloader) # 배치 개수
for epoch in range(200): # 200번 학습
running_loss = 0.0
for data in trainloader: # 데이터 배치 단위로 가져오기
inputs, values = data # 입력값과 출력값 분리
optimizer.zero_grad() # 이전 기울기 초기화
outputs = model(inputs) # 모델에 데이터 입력 -> 예측값 산출
loss = criterion(outputs, values) # 예측값과 실제값 비교 -> 손실 계산
loss.backward() # 손실을 기준으로 역전파 수행
optimizer.step() # 가중치 업데이트
running_loss += loss.item() # 배치 손실 합산
l = running_loss / n # 에포크당 평균 손실 계산
loss_.append(l) # 손실 기록
- 데이터 준비: 배치 단위로 데이터를 가져온다.
- 순전파: 입력 데이터를 통해 예측값을 생성한다.
- 손실 계산: 예측값과 실제값 간의 차이를 계산한다.
- 역전파 및 업데이트: 손실을 줄이는 방향으로 모델의 가중치를 조정한다.
- 손실 추적: 한 에포크의 평균 손실 값을 기록한다.
학습 중 모델 저장
if l < ls: # 현재 에포크의 손실(l)이 이전까지의 최소 손실(ls)보다 작다면
ls = l # 최소 손실 값을 현재 손실로 업데이트
ep = epoch # 최소 손실이 기록된 에포크를 저장
torch.save({'epoch': ep, # 에포크 정보 저장
'loss': loss_, # 손실 기록 리스트 저장
'model': model.state_dict(), # 모델의 학습된 가중치 저장
'optimizer': optimizer.state_dict() # 옵티마이저 상태 저장
}, './models/reg4-1.pt') # 모델을 reg4-1.pt 파일로 저장최적의 모델만 저장:
모든 에포크의 모델을 저장하면 불필요한 저장 공간 낭비와 관리의 어려움이 발생한다.
손실 값이 줄어들 때만 저장하여 최적의 상태를 기록한다.학습 중단/재개 가능:
저장된 모델을 불러와 이전 학습 상태에서 이어갈 수 있다. 예를 들어, 서버가 중단되거나 장시간 학습을 할 때 유용하다.평가/배포 시 유용:
학습이 완료된 모델을 다시 학습할 필요 없이, 저장된 상태를 불러와 곧바로 평가나 예측에 사용할 수 있다.+model.state_dict()와 torch.save()의 차이:
model.state_dict()는 모델의 학습된 파라미터(가중치와 바이어스)만 저장한다.
torch.save()는 다양한 정보를 저장할 수 있어 재학습 시 편리하다.
학습 결과 저장 및 시각화
plt.plot(loss_)
plt.title("Training Loss")
plt.xlabel("epoch")
plt.savefig("loss.png")저장된 모델 불러오기
checkpoint = torch.load ('./models/reg4-1.pt', weights_only=True)# 저장된 모델 상태를 불러온다
model.load_state_dict(checkpoint['model'])# 저장된 모델의 가중치를 모델에 로드한다
optimizer.load_state_dict(checkpoint['optimizer'])# 저장된 옵티마이저 상태를 옵티마이저에 로드한다
loss_ = checkpoint['loss']# 저장된 손실 기록 리스트를 불러온다
ep = checkpoint['epoch']# 저장된 에포크를 불러온다
ls = loss_[-1]# 저장된 손실 기록 중 마지막 값을 불러온다
print(f"epoch={ep}, loss={ls}")모델 평가
def rmse(dataloader):
with torch.no_grad():
square_sum = 0
num_instances = 0
model.eval() # 평가 모드
for data in dataloader:
inputs, targets = data
outputs = model(inputs)
square_sum += torch.sum((outputs - targets) ** 2).item()
num_instances += len(targets)
model.train()
return np.sqrt(square_sum / num_instances)
train_rmse = rmse(trainloader) # 학습 데이터 RMSE
test_rmse = rmse(testloader) # 테스트 데이터 RMSE
print("Train RMSE: %.5f" % train_rmse)
print("Test RMSE: %.5f" % test_rmse)
- with torch.no_grad():
평가 시에 사용한다. 역전파 계산을 비활성화해 메모리 사용량과 계산 시간을 줄인다.
학습이 아닌 단순 평가를 목적으로 하므로 필요 없는 기울기 계산을 방지한다.
model.eval()
모델을 평가 모드로 전환한다.
학습 중에 사용된 드롭아웃(Dropout)과 배치 정규화(Batch Normalization)를 비활성화한다.
예측 시에는 이러한 기법이 적용되지 않아야 정확한 평가가 가능하다.루프를 통한 데이터 처리
for data in dataloader:는 데이터 로더에서 배치를 하나씩 가져온다.
inputs는 입력 데이터이고, targets는 실제 정답 값이다.
outputs = model(inputs)는 모델에 데이터를 넣어 예측값을 얻는다.
- 오차 제곱 합 계산
(outputs - targets) ** 2는 예측값과 실제값의 차이를 제곱한다.
torch.sum으로 모든 샘플의 오차 제곱을 합산한다.
square_sum은 누적된 오차 제곱 합을 저장한다.
- 총 샘플 수 계산
len(targets)는 현재 배치에 포함된 샘플의 개수를 반환한다.
num_instances는 전체 데이터의 총 샘플 개수를 누적한다.
- model.train()
함수가 끝나기 전에 모델을 다시 학습 모드로 전환한다.
이후 학습을 진행할 때 모델의 동작이 정상적으로 돌아가도록 한다.
- np.sqrt
오차 제곱 합을 샘플 개수로 나누어 평균 제곱 오차(MSE)를 계산한다.
이 값을 제곱근으로 변환해 RMSE를 반환한다.
학습 데이터와 테스트 데이터 평가
train_rmse = rmse(trainloader) # 학습 데이터 RMSE
test_rmse = rmse(testloader) # 테스트 데이터 RMSE결과 출력
print("Train RMSE: %.5f" % train_rmse)
print("Test RMSE: %.5f" % test_rmse)