선형 회귀의 사례

몸무게와 키의 상관관계 찾아내기

방정식을 배운 머신이는 몸무게와 키의 데이터를 획득했다. 일정하게 증가하는 패턴이 있어서 미리 몸무게를 알면 키를 알 수 있을 것이라고 생각했다.

• 키와 몸무게 간의 데이터

weights = [87,81,82,92,90,61,86,66,69,69]
heights = [187,174,179,192,188,160,179,168,168,174]

• 키와 몸무게 간의 산점도
  

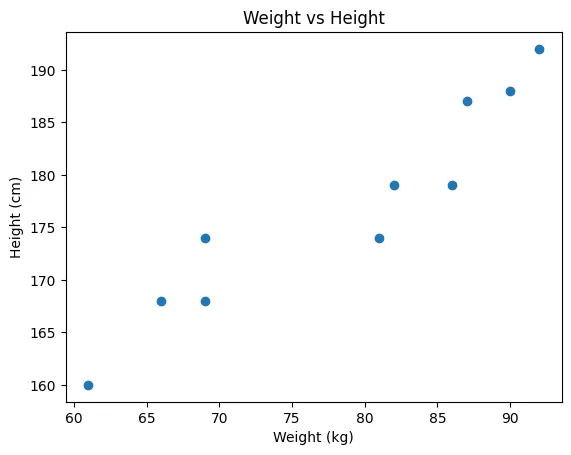
• 어떤 직선이 현재 데이터를 잘 '설명'한다고 할 수 있을까?
  
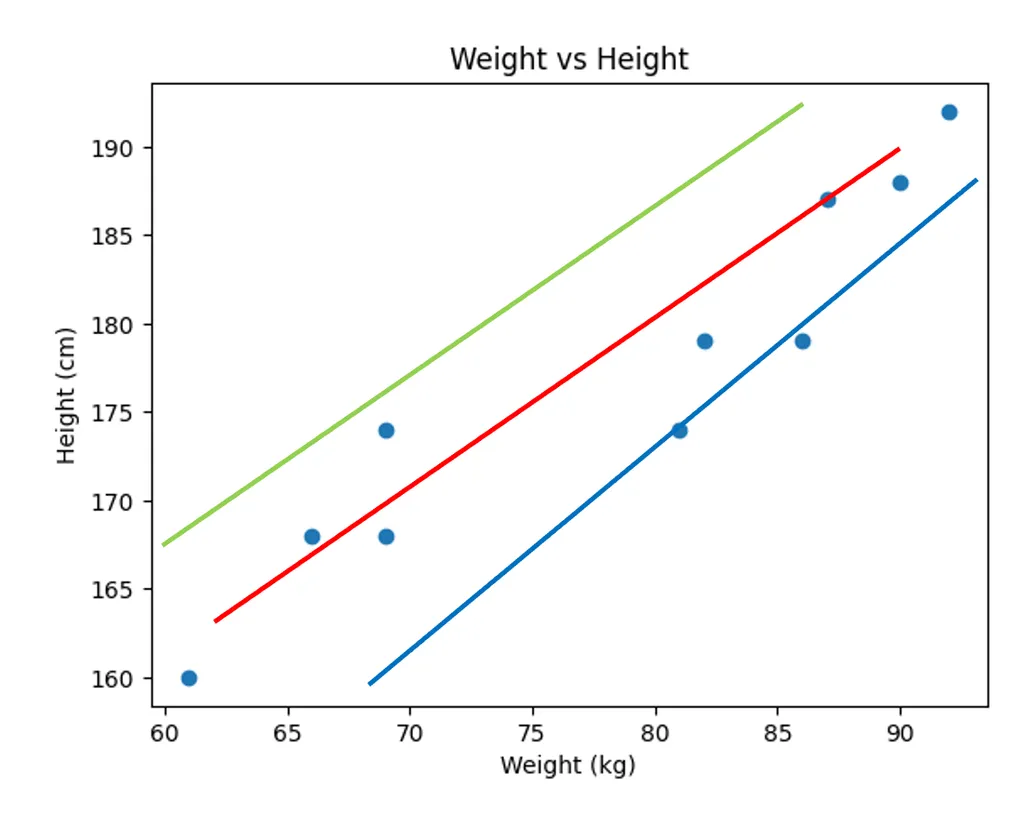
  아무래도 빨간 그래프가 적절한 것 같다. 하지만 이렇게 대강 직선을 그리다보면 적절한 그래프를 찾기 어려울 것 같아 고민에 빠졌다.

Data Scientific한 발상

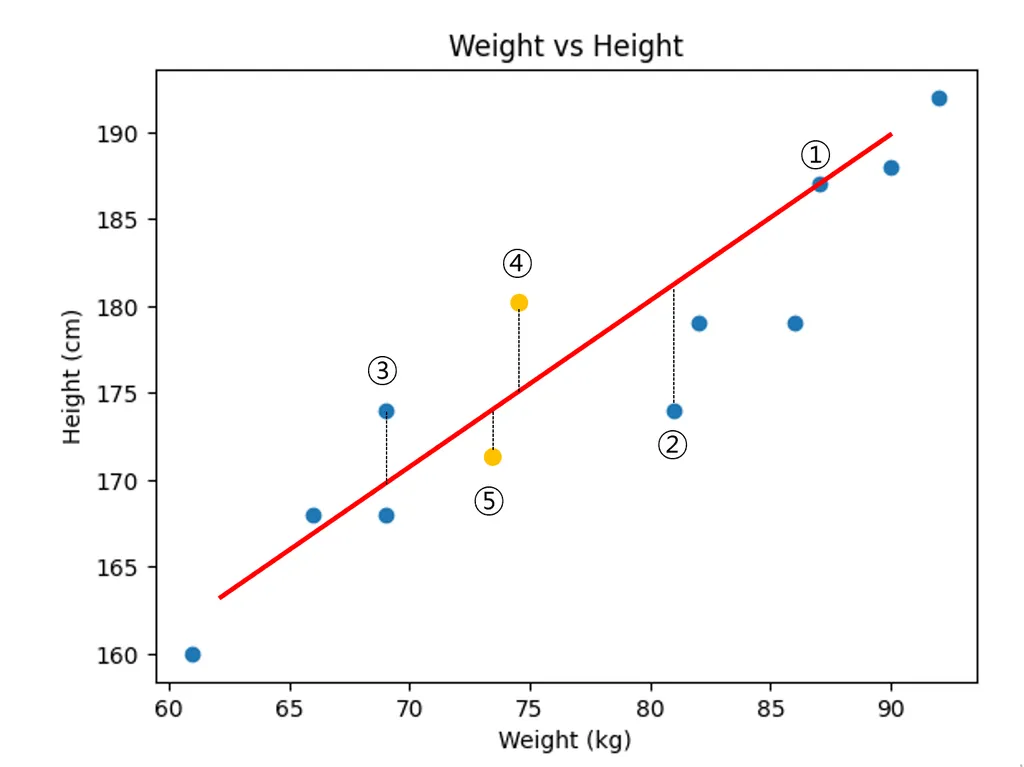
머신이는 하나의 생각을 떠 올렸다. 바로 직선과 점의 간의 거리를 계산하는 것이다. 이를 Error 라고 정의하고 최소의 Error인 직선을 그리면 된다고 생각했다.

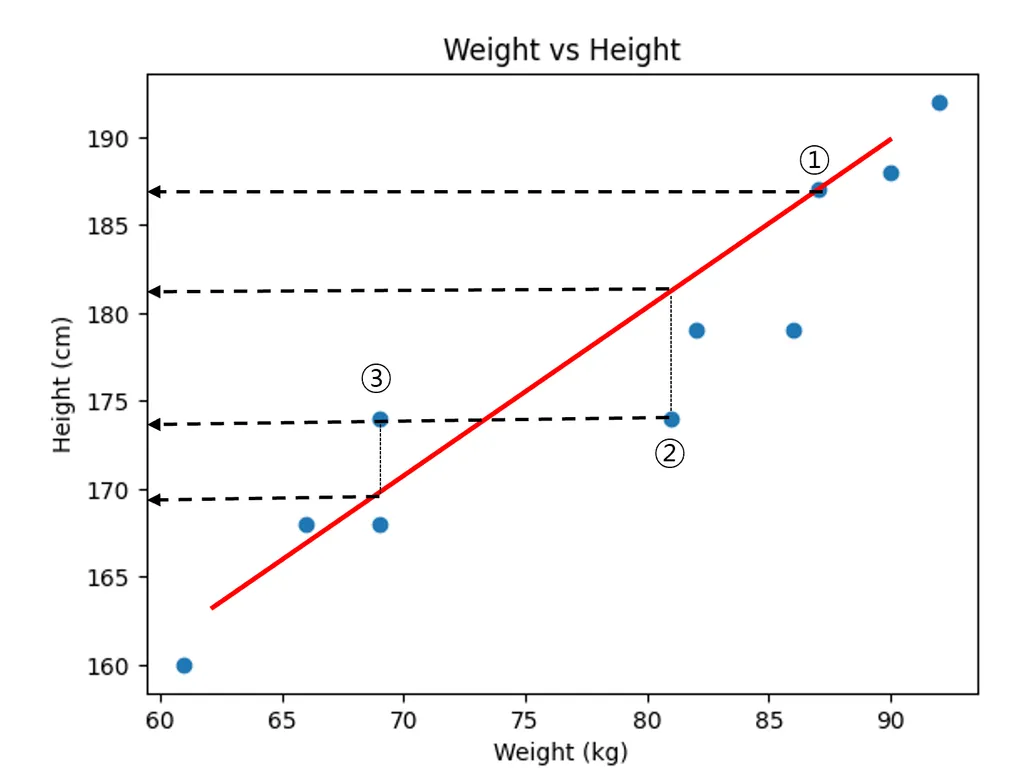
• 실제 데이터 값 - 직선의 예측 값 오차 구하기
• 음수와 양수가 상쇄되는 것을 막기 위해 제곱하여 오차 더하기
• 데이터의 수가 많아질수록 오차가 커지는 것을 막기 위해 데이터의 개수로 오차의 합 나누기
• 제곱이 된 것을 줄이기 위해 루트를 씌우

선형 회귀 이론

용어

공통

• $Y$: 종속 변수, 결과 변수
• $X$: 독립 변수, 원인 변수, 설명 변수

통계학

• 선형회귀식

  $Y = \beta_0 + \beta_1X + \varepsilon$

• $\beta_0$: 편향 Bias
• $\beta_1$: 회귀 계수
• $\varepsilon$: 오차, 에러. 모델이 설명하지 못하는 $Y$의 변동성

머신러닝/딥러닝

• 선형회귀식

  $Y = wX+b$

• $w$: 가중치

• $b$: 편향 bias

두 수식의 의미는 같음. 회귀계수 혹은 가중치의 값을 알면 X가 주어졌을 때 Y를 알 수 있다.

회귀 분석 평가 지표

Mean Square Error, MSE

1. 에러 = 실제 데이터 - 예측 데이터 로 정의하기

$\varepsilon = y_i - \hat{y_i}$

2. 에러를 제곱하여 모두 양수로 만든 후 합치기

$\sum_{i=1}^n(y_i - \hat{y_i})^2$

3. 데이터 수로 나누기

$\frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{n}$

RMSE

• MSE에 루트를 씌워 제곱된 단위를 다시 맞춘 지표

$RMSE = \sqrt{\frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{n}}$

MAE

• Mean Absolute Error, 제곱 대신 절대값을 이용하여 오차 계산

$MAE = \frac{1}{n}\sum_{i=1}^n\vert y_i - \hat{y_i}\vert$

R-square 결정계수

전체 모형에서 회귀선으로 설명할 수 있는 정도.
독립변수가 종속변수를 얼마나 잘 설명하는지 나타냄.

• $y_i$: 특정 데이터의 실제 값
• $\bar y$: 평균값
• $\hat y$: 예측값, 추정값

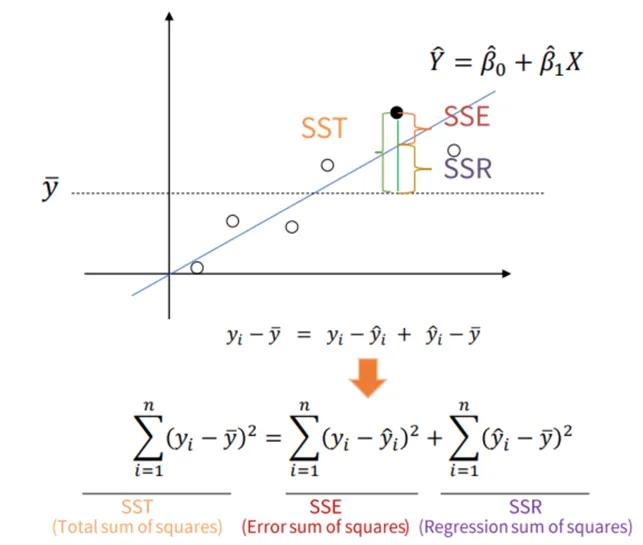
• SST = Total Sum of Squares, 평균과 실제 값의 차이. 종속변수의 총 변동.
• SSE = Error of Squares, 회귀선과 실제 값의 차이.
• SSR = Regression Sum of Squares, 평균과 회귀선의 차이. 회귀모델에 의해 설명되지 않는 변동.

$R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}= \frac{SSR}{SSR + SSE}$

• 전체에서 회귀선이 설명하지 못하는 부분을 뺀 값. 즉, 회귀선이 설명할 수 있는 부분.
• 회귀선이 얼마나 설명할 수 있는지.
• 0과 1 사이의 값을 가지며 1에 가까울수록 설명력이 높은 것.

실습

자주 쓰는 함수

• sklearn.linear_mode.LinearRegression
  • coef_: 회귀 계수
  • intercept_: 편향 (bias)
  • fit: 데이터 학습
  • predict: 데이터 예측

키-몸무게 데이터 실습

라이브러리 불러오기 및 데이터 생성

import sklearn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

weights = [87, 81, 82, 92, 90, 61, 86, 66, 69, 69]
heights = [187, 174, 179, 192, 188, 160, 179, 168, 168, 174]
print(len(weights))
print(len(heights))

# 10
# 10

# dictionary 형태로 데이터 생성
body_df = pd.DataFrame({'height' : heights, 'weight' : weights})
body_df.head(3)

weight와 height 간의 산점도 확인하기

# weight와 height간의 산점도(scatter plot)
sns.scatterplot( data = body_df, x = 'weight', y = 'height')
plt.title('Weight vs Height')
plt.xlabel('weight(kg)')
plt.ylabel('Height (cm)')
plt.show()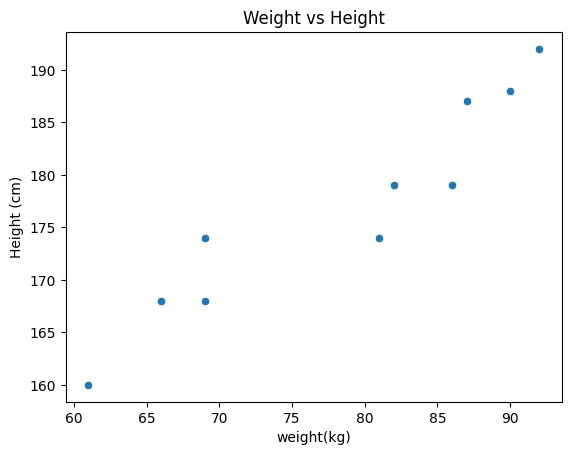

선형 회귀 훈련

from sklearn.linear_model import LinearRegression
model_lr = LinearRegression()

# 입력값 미리 정의
X = body_df[['weight']]
y = body_df[['height']]
# DataFrame[]: Series(데이터 프레임의 컬럼)
# DataFrame[[]]: DataFrame

# 데이터 훈련
model_lr.fit(X = X, y = y)

확인

# 가중치(w1)
print(model_lr.coef_)

# 편향(bias, w0)
print(model_lr.intercept_)

# [[0.86251245]]
# [109.36527488]

w1 = model_lr.coef_[0][0]
w0 = model_lr.intercept_[0]

print('y = {}x + {}'.format(w1.round(2),w0.round(2)))

# y = 0.86x + 109.37

y(height)는 x(몸무게)에 0.86을 곱한뒤 109.37을 더하면 된다.

예측값 구하기

body_df['pred'] = body_df['weight'] * w1 + w0
body_df.head(3)

에러 구하기

body_df['error'] = body_df['height'] - body_df['pred']
body_df['error^2'] = body_df['error']*body_df['error']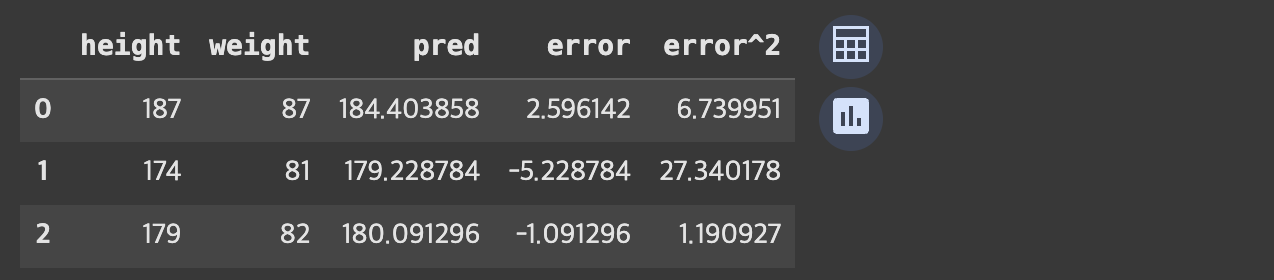

MSE 계산

body_df['error^2'].sum()/len(body_df)
# 10.152939045376309

그래프로 확인하기

sns.scatterplot(data = body_df, x = 'weight', y = 'height')
sns.lineplot(data = body_df, x = 'weight', y = 'pred', color = 'red')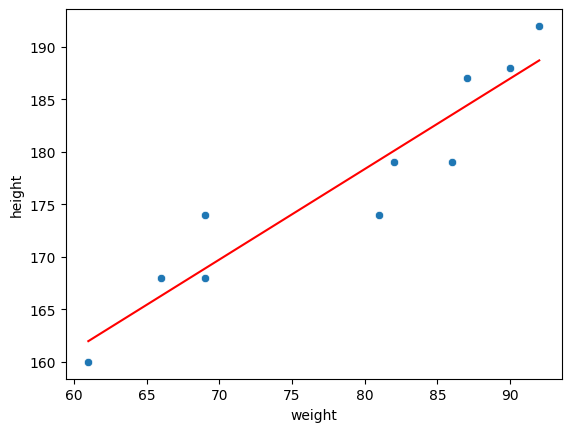

모델 평가하기

from sklearn.metrics import mean_squared_error, r2_score

# 평가함수는 공통적으로 정답(실제 true), 예측값(pred) 입력
y_true = body_df['height']
y_pred = body_df['pred']

# MSE
mean_squared_error(y_true, y_pred)
# 10.152939045376309

# R square
r2_score(y_true, y_pred)
# 0.8899887415172141

예측값을 구하는 다른 방법

y_pred2 = model_lr.predict(body_df[['weight']])
y_pred2

# 결과
array([[184.40385835],
       [179.22878362],
       [180.09129608],
       [188.71642061],
       [186.99139571],
       [161.97853455],
       [183.54134589],
       [166.29109682],
       [168.87863418],
       [168.87863418]])
       
# 확인
mean_squared_error(y_true,y_pred2)
# 10.152939045376318

tips 데이터 실습

데이터 불러오기 및 확인

tips_df = sns.load_dataset('tips')
tips_df.head(3)

• 이 중 'total bill'(X)과 'tip'(Y)을 각각 독립변수와 종속변수로 설정하기로 함.

산점도로 데이터 분포 확인

sns.scatterplot(data = tips_df, x = 'total_bill', y=  'tip')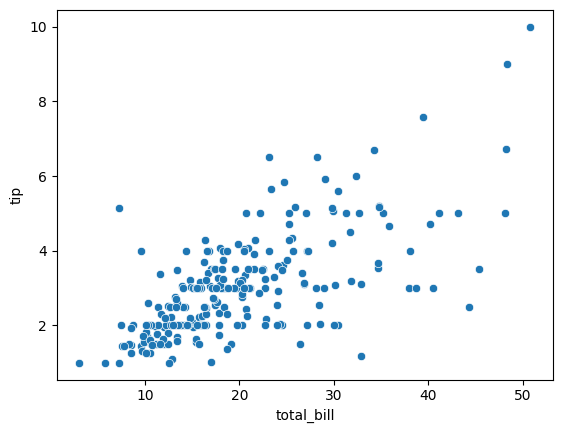

모델 학습 및 결과 확인

# 학습
model_lr2 = LinearRegression()
X = tips_df[['total_bill']]
y = tips_df[['tip']]
model_lr2.fit(X,y)

# 확인
# y(tip) = w1*x(total_bill) + w0
w1_tip = model_lr2.coef_[0][0]
w0_tip = model_lr2.intercept_[0]

print('y = {}x + {}'.format(w1_tip.round(2), w0_tip.round(2)))
# y = 0.11x + 0.92

• 전체 결제금액이 1달러 오를때, 팁은 0.11달러 추가된다.
• 전체 결제금액이 100달러 오를때, 팁은 11달러 추가된다.

예측값 생성

y_true_tip = tips_df['tip']
y_pred_tip = model_lr2.predict(tips_df[['total_bill']])

평가하기

# MSE
mean_squared_error(y_true_tip, y_pred_tip)
# 1.036019442011377

# R square
r2_score(y_true_tip, y_pred_tip)
# 0.45661658635167657

그래프로 나타내기

# 데이터프레임에 예측값 추가
tips_df['pred'] = y_pred_tip

sns.scatterplot(data = tips_df, x = 'total_bill', y=  'tip')
sns.lineplot(data = tips_df, x = 'total_bill', y = 'pred', color = 'red')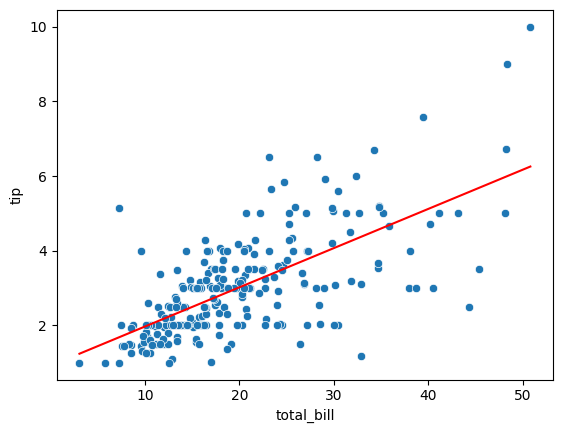

선형 회귀 심화

다중선형회귀

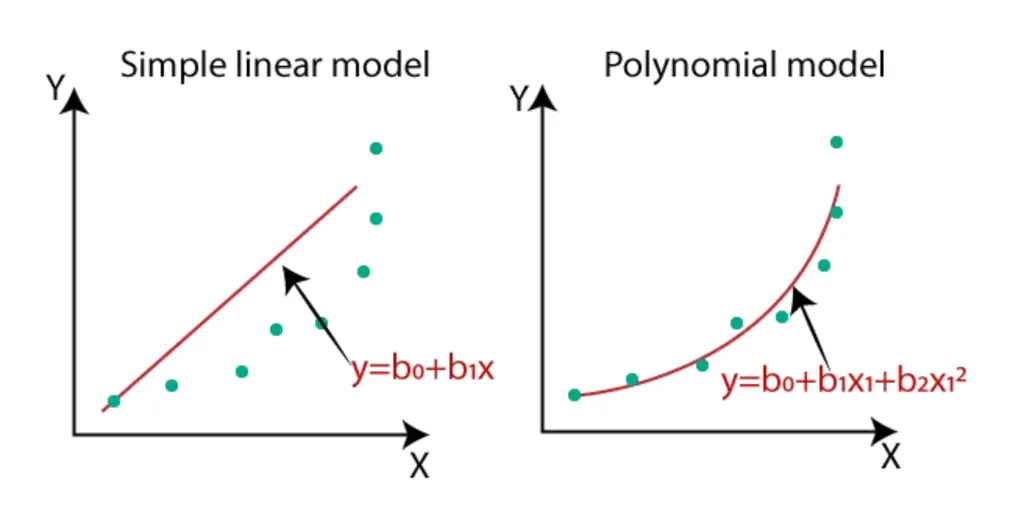
지금까지는 X와 Y간의 데이터에 아주 간단한 단순회귀분석에 대해서만 배웠지만 실제의 데이터들은 비선형적 관계를 가지는 경우가 많습니다. 이를 위해서 X변수를 추가 할 수도, 변형할 수 도 있습니다.

• 단순선형회귀 vs 다항회귀

범주형 데이터 사용하기

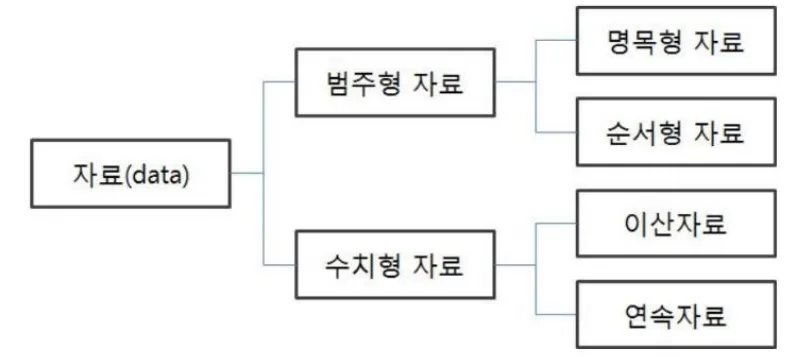
• 수치형 데이터
  • 연속형 데이터: 값이 무한한 개수로 나누어진 데이터. ex) 키, 몸무게 등
  • 이산형 데이터: 유한한 개수로 나누어진 데이터. ex) 주사위 눈 개수, 나이 등
• 범주형 데이터
  • 순서형 데이터: 데이터에 순서가 있음. ex) 학점, 등급 등
  • 명목형 자료: 데이터에 순서 의미가 없음. ex) 혈액형, 성별 등

범주형 데이터 실습

머신이는 데이터 선형회귀를 훈련 시켰지만 성능이 별로 좋지 않다는 것을 알게 되었습니다. 그래서 성별과 같은 다른 데이터를 사용하고 싶어졌습니다. 그런데 문제는 성별데이터는 문자형이여서 숫자로 표현할 방법이 필요해졌습니다.

• 범주형 데이터를 훈련시키기 위해서는 해당 데이터를 숫자로 바꾸어야 함
• 범주형 데이터를 임의로 0, 1 등의 숫자로 바꿀 수 있음. (Encoding)

데이터 확인

tips_df.head(3)

범주형 데이터 전처리

# Female 0, Male 1 
def get_sex(x):
    if x == 'Female':
        return 0
    else:
        return 1
        
#apply method는 매 행을 특정한 함수를 적용한다.
tips_df['sex_en'] = tips_df['sex'].apply(get_sex)
tips_df.head(3)

모델 학습시키기

model_lr3 = LinearRegression()

X = tips_df[['total_bill','sex_en']]
y = tips_df[['tip']]

model_lr3.fit(X,y)

예측하기

y_pred_tip2 = model_lr3.predict(X)
y_pred_tip2[:5]

# 결과
array([[2.72117624],
       [1.99477235],
       [3.1176016 ],
       [3.39857199],
       [3.52094215]])

평가

# 단순선형회귀 mse: X변수가 전체 금액
# 다중선형회귀 mse: X변수가 전체 금액, 성별

# MSE
print('단순선형회귀', mean_squared_error(y_true_tip, y_pred_tip))
print('다중선형회귀', mean_squared_error(y_true_tip, y_pred_tip2))
# 단순선형회귀 1.036019442011377
# 다중선형회귀 1.0358604137213614

# R square
print('단순선형회귀', r2_score(y_true_tip, y_pred_tip))
print('다중선형회귀', r2_score(y_true_tip, y_pred_tip2))
# 단순선형회귀 0.45661658635167657
# 다중선형회귀 0.45669999534149974

• 평가지표에서 큰 차이는 없다.
• 'sex'를 독립변수로 설정하기 전, 실제로 해당 컬럼과 종속변수인 'tip' 사이의 유의미한 관계가 있는지 확인했어야.

ex)

회귀분석에서의 t-검정

• 회귀분석 진행 시 모든 $\beta$에 대해서 검정 진행

• 귀무가설 : $\beta$는 0이다. 즉, Y에 영향이 없다.
• 대립가설: $\beta$는 0이 아니다.

• 어떤 변수에 대한 t검정의 p-value 값이 유의수준보다 작다면 그 변수는 영향이 있다고 할 수 있고, coef 값을 믿고 사용할 수 있다.

선형 회귀의 가정

선형성 Linearity

• 종속 변수 Y와 독립 변수 X 간에 선형 관계가 존재해야 함

등분산성 Homoscedasticity

• 오차의 분산이 모든 수준의 독립 변수에 대해 일정해야 함
• 즉, 오차가 특정 패턴을 보여서는 안되며, 독립변수의 값에 상관 없이 일정해야
  
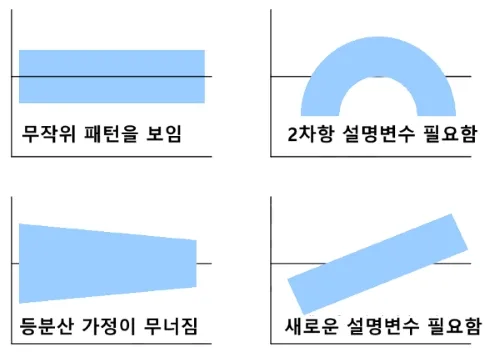
  X축: 독립변수 Y축: 에러

정규성 Normality

• 오차항은 정규 분포를 따라야 한다

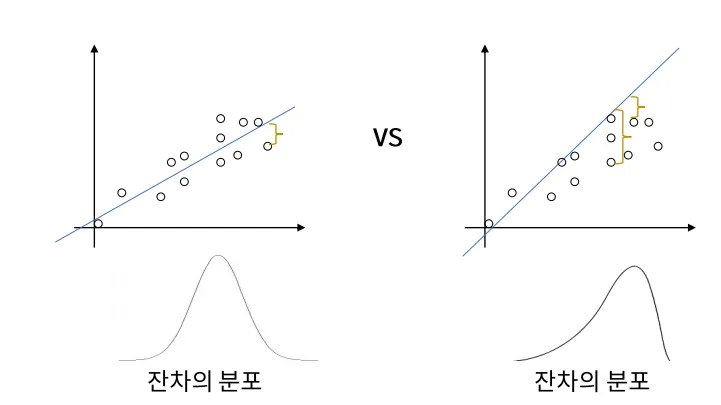
독립성 Independence

• X 변수는 서로 독립적이어야 한다

다중공선성 Multicolinearity

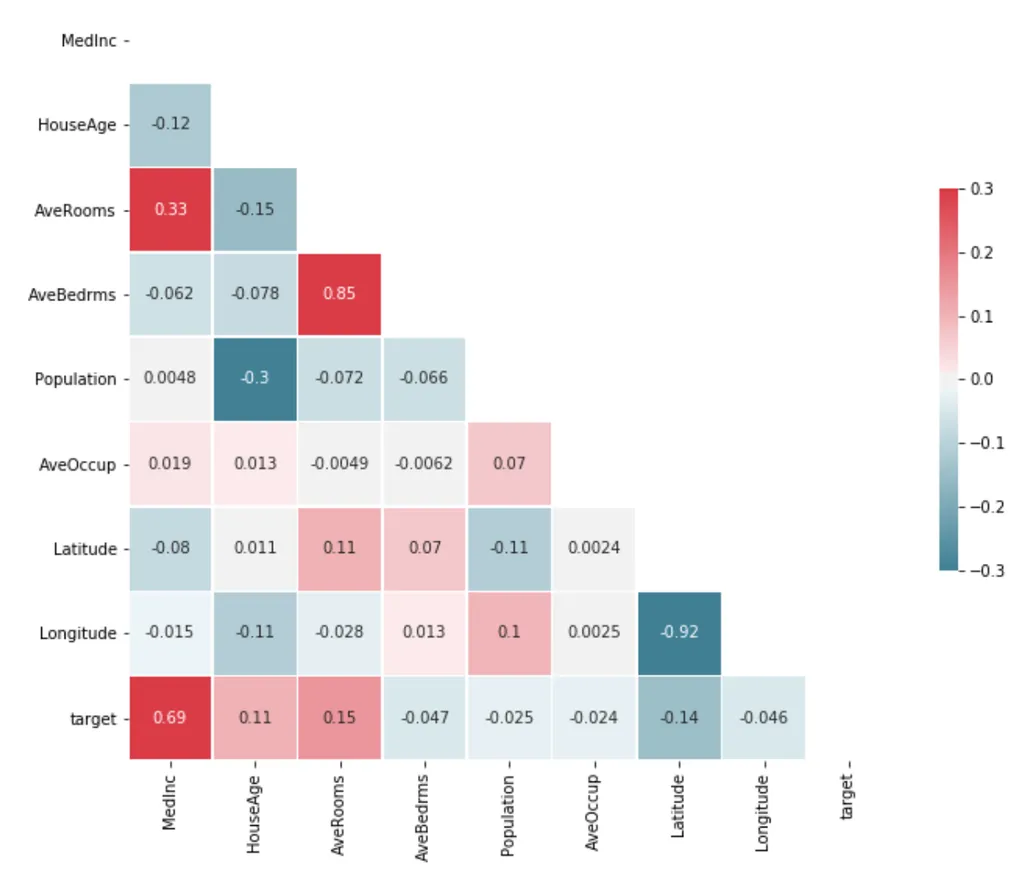
변수가 많아지면 서로 연관이 있는 경우가 많다. 이처럼 회귀분석에서 독립변수(X)간의 강한 상관관계가 나타나는 것을 다중공선성(Multicolinearity)문제라고 한다.

• 만약 위 Weight-Height 외에 다른 변수를 가지고 Y(발 사이즈 등)를 예측한다고 하면, Weight와 Height가 서로 연관이 있는 변수이기 때문에 다중공선성 문제가 발생.

해결 방법

• 산점도 혹은 상관관계 행렬을 확인하여 서로 상관관계가 높은 변수 중 하나만 채택
  
  

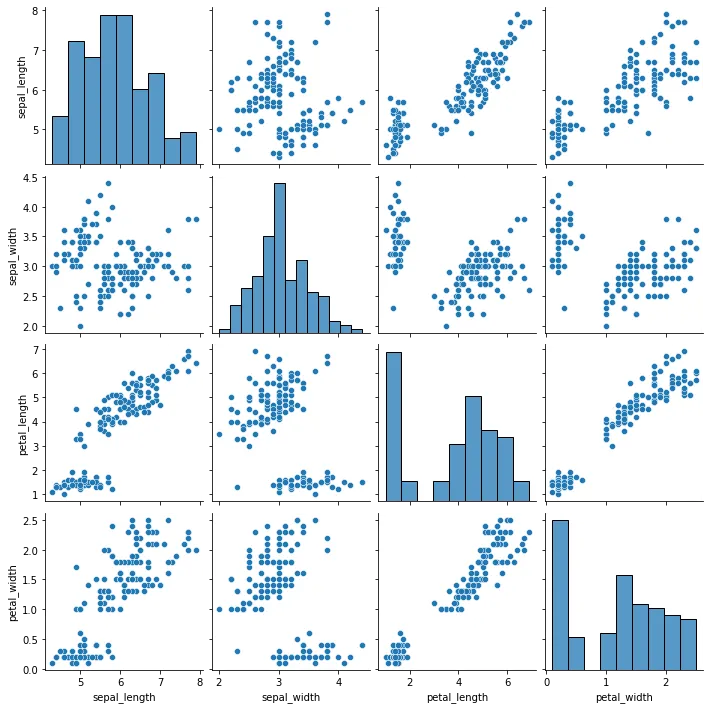
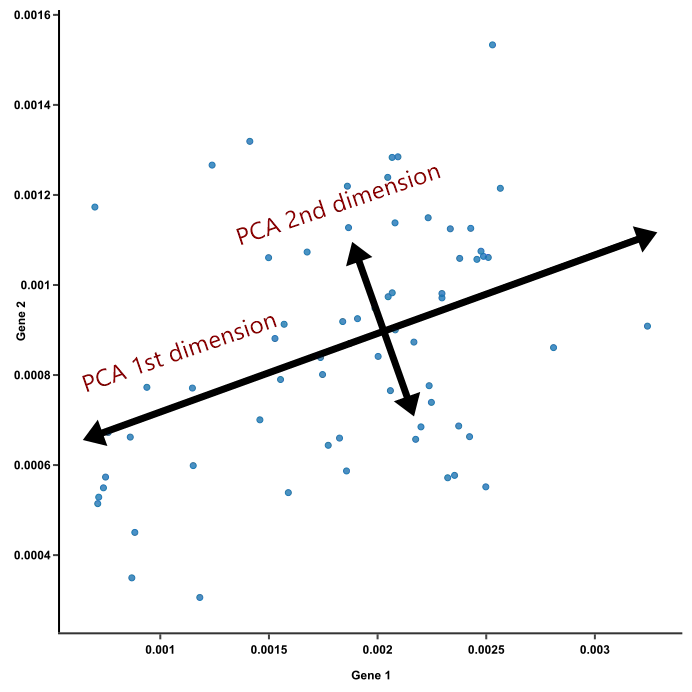
• 두 변수를 동시에 설명하는 차원축소 (Principle Component Analysis, PCA)를 실행
  

정리

선형회귀의 장점

• 직관적이며 이해하기 쉽다.
• X-Y 관계를 정량화할 수 있다.
• 모델이 빠르게 학습된다.

선형회귀의 단점

• X-Y간의 선형성 가정이 필요하다.
• 평가지표가 평균을 포함하기에 이상치에 민감하다.
• 범주형 변수를 인코딩하면 정보 손실이 일어난다. (0, 1, 2이 각각 부산인지 대구인지 광주인지 모름)