의사결정 나무 Decision Tree

의사결정 규칙을 트리 구조로 나타내여 전체 자료를 몇 개의 소집단으로 분류하여 예측을 수행하는 분석 방법

개념 및 용어

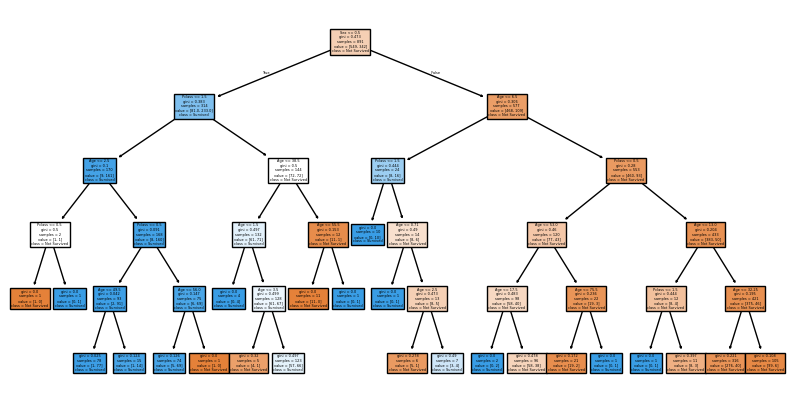
• 루트 노드(Root Node): 의사결정나무의 시작점. 최초의 분할조건
• 리프 노드(Leaf Node): 루트 노드로부터 파생된 중간 혹은 최종 노드
• 분류기준(criteria): 여성인 경우 0, 남성인 경우 1로 인코딩. 여성인 경우 좌측 노드로, 남성인 경우 우측 노드로 분류
• 불순도(impurity)
  • 지니 계수: 0과 1사이 값으로, 0이 완벽한 순도(모든 샘플이 하나의 클래스), 1은 완전한 불순도(노드의 샘플의 균등하게 분포) 를 나타냄
  • 리프 노드로 갈수록 불순도가 작아지는(한쪽으로 클래스가 분류가 잘되는)방향으로 나무가 자람
• 샘플(samples): 해당 노드의 샘플 개수(891개의 관측치)
• 값(value): Y변수에 대한 배열. 549명이 죽었고(Y = 0), 342명이 살았음(Y = 1)
• 클래스(class)
  • 가장 많은 샘플을 차지하는 클래스를 표현
  • 위에서는 주황색(Y = 0 다수), 파란색(Y=1 다수)를 표현

장점

• 해석이 쉽고 용이
• 다중 분류와 회귀에 모두 적용 가능 (회귀의 경우 평균 이용)
• 이상치에 쉽게 영향을 받지 않으며 데이터 스케일링 불필요

단점

• 트리가 성장을 과도하게 하는 경우 오버피팅에 취약
• 훈련 데이터에 민감하게 반응하여 작은 변화나 노이즈에도 트리 구조가 크게 달라짐 (불안정성)

실습

• sklearn.tree.DecisionTreeClassifier
• sklearn.tree.DecisionTreeRegressor

X_features = ['Pclass','Sex','Age']
# Pclass: LabelEncoder
# Sex: LabelEncoder
# Age: 결측치-> 평균으로 대치하고 

le = LabelEncoder()
titaninc_df['Sex'] = le.fit_transform(titaninc_df['Sex'])

le2 = LabelEncoder()
titaninc_df['Pclass'] = le2.fit_transform(titaninc_df['Pclass'])

age_mean = titaninc_df['Age'].mean()
titaninc_df['Age'] = titaninc_df['Age'].fillna(age_mean)


X = titaninc_df[X_features]
y = titaninc_df['Survived']

model_dt = DecisionTreeClassifier()
model_dt.fit(X,y)

plt.figure(figsize = (10,5))
plot_tree(model_dt, feature_names=X_features, class_names=['Not Survived','Survived'], filled= True)
plt.show()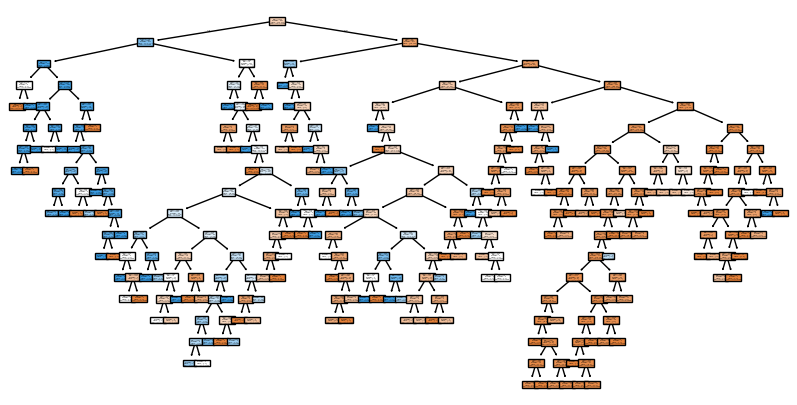

과적합을 방지하기 위한 max_depth 설정

• 과적합을 방지하기 위해 의사결정나무 분류기에 최대 깊이를 설정해줄 수 있다.
• max_depth = 5로 설정한 후의 결과를 시각화 하면 아래와 같다.

model_dt = DecisionTreeClassifier(max_depth = 5)
model_dt.fit(X,y)

plt.figure(figsize = (10,5))
plot_tree(model_dt, feature_names=X_features, class_names=['Not Survived','Survived'], filled= True)
plt.show()