미리보기

t-test (2~3개 집단 비교)

두 모집단의 표준편차가 알려지지 않았을 때, 정규분포 모집단에서 모은 샘플의 평균값에 대한 가설 검정입니다.
즉, 표본 두 집단이 통계적으로 같은지 다른지 비교하는 테스트입니다.

t-test는 다소 간단하면서 가장 많이 이루어지며, 엑셀로도 진행할 수 있습니다.

[상황]
A반과 B반의 학생들 평균 몸무게는 60kg, 62kg 이라고 할 때, 통계적 관점으로 본다면
두 반의 몸무게 평균 차이 2kg은 우연히 발생한 것인지(같은것인지) 아닌지(다른것인지) 비교하는 테스트로 진행할 수 있습니다.

표준 편차 : 데이터가 의미없이 퍼져 있는 정도
평균이 동일(비슷)해도, 표준편차가 다르다면 두 집단의 데이터 분포 형태는 다릅니다.

1. 대응표본 t-test

표본 집단 1개를 특정값과 비교하는 경우
(A반 학생들의 몸무게 평균은 50kg이상인가?)

2. 대응표본(쌍체) t-test

1개 집단을 실험 전과 후로 비교하는 경우
(A반 학생들의 평균몸무게는 추석 이전과 이후가 같은가? )

3. 독립표본 t-test

두 표본 집단을 비교하는 경우
(A반과 B반 학생들의 평균 몸무게는 같은가 다른가? )

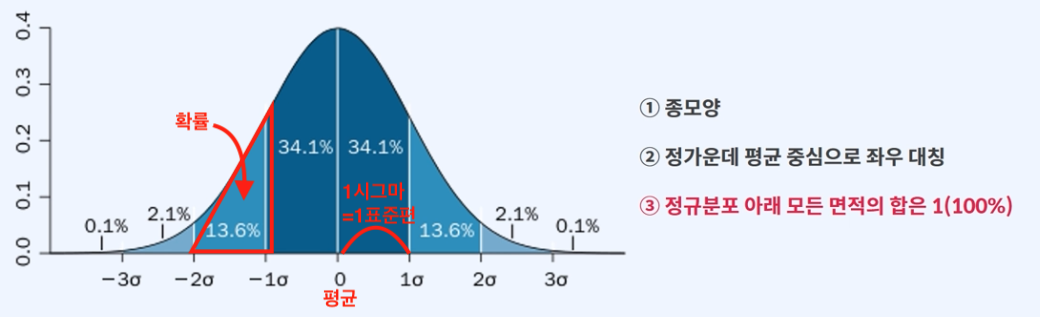
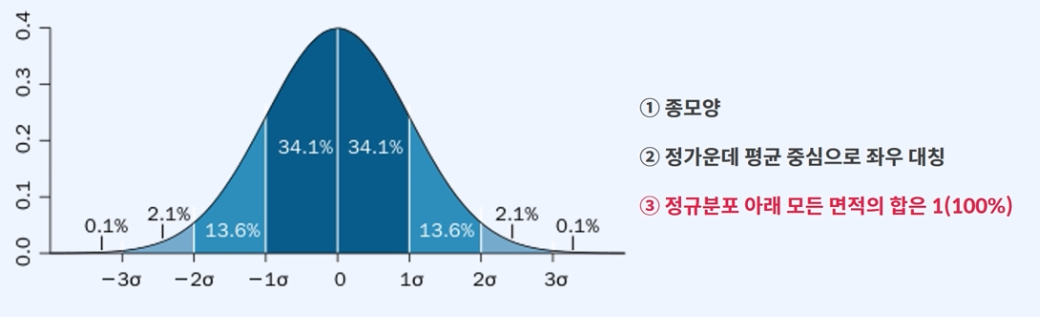
정규분포

[상황]
A반 학생 100명의 몸무게 평균은 60kg이고 표준편차가 5일때,
몸무게가 60~65kg인 학생은 몇 명 일까요?

몸무게 60~65kg 사이의 면적 34.1% 로 확인됩니다.
따라서 확률상 100명 중 약 34명 입니다.

t-test의 T-table

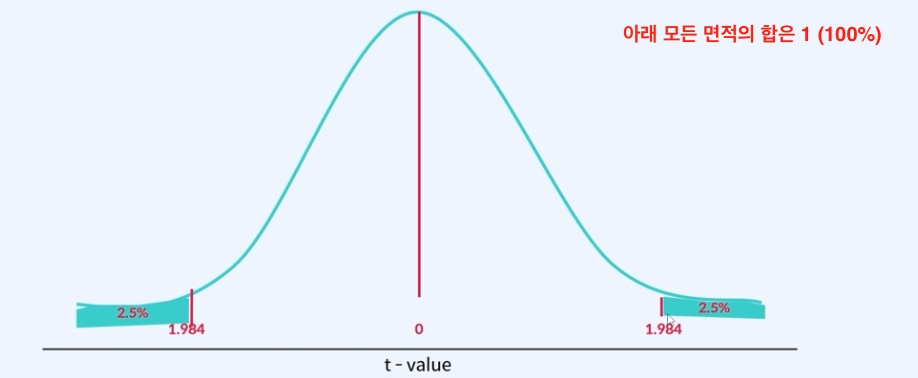
[상황]
어떠한 값이 1.984보다 커서 (예를 들면 2.1) 2.5% 안에 들어가게 된다면,
비교하고자 하는 두 집단 혹은 한 집단의 표본의 평균은 다르다 라고 결과에 대해 말할 수 있습니다.

t-value값 (예를 들면 2.1) 기준으로
두 집단이 다를 확률이 5% 또는 1% 보다 작으면, 우연이 발생한 것이 아니다 라고 말 할 수 있습니다.

양측검정, 단측검정

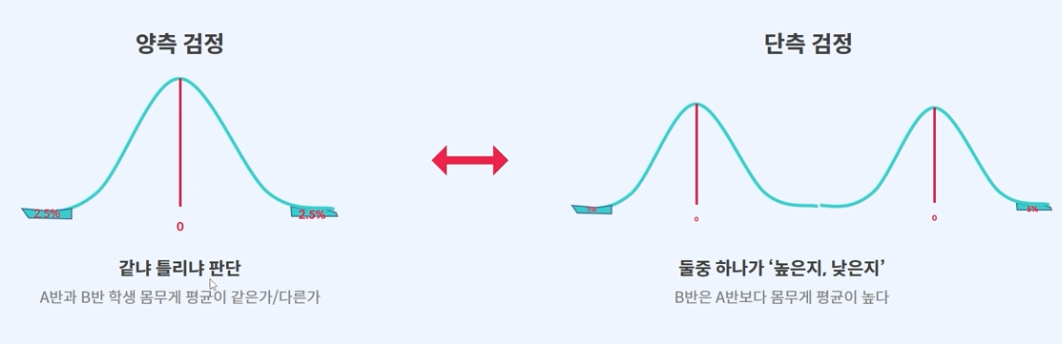
같냐 틀리냐 판단하고 싶을 땐, 양측검정
둘 중 하나가 높은지 낮은지 판단하고 싶을 땐, 단측검정

둘 다 모두 value값이 5% (0.05) 이내 여야 우연히 일어난게 아니다 = 두 집단은 서로 다르다 라는 결론이 나옵니다.

t-test적용 공식