미리보기

---

데이터

회원들의 매출만을 가지고, 매출의 차이를 통계적으로 유의미한지 (통계적으로 차이가 있는지) 알아보겠습니다.

• 가상의 백화점에서 2023년 5월에 실시한 행사의 매출에 대해서, 작년 2022년 5월 매출 평균과 비교해보며 통계적으로 유의미한 행사 결과를 얻어냈는지 데이터 검정을 실시
• 2022년 5월에 비해, 2023년 5월에는 광고 및 행사 비용을 더 지원하였음
• 방문 고객당 평균 매출을 기준으로 비교
• 두 데이터를 비교 할 때, 공통피쳐(유저)를 기준으로 비교

countif함수

=countif(범위, 기준값)
범위 내에 기준값이 몇 개가 있는지 확인됩니다.

피벗테이블

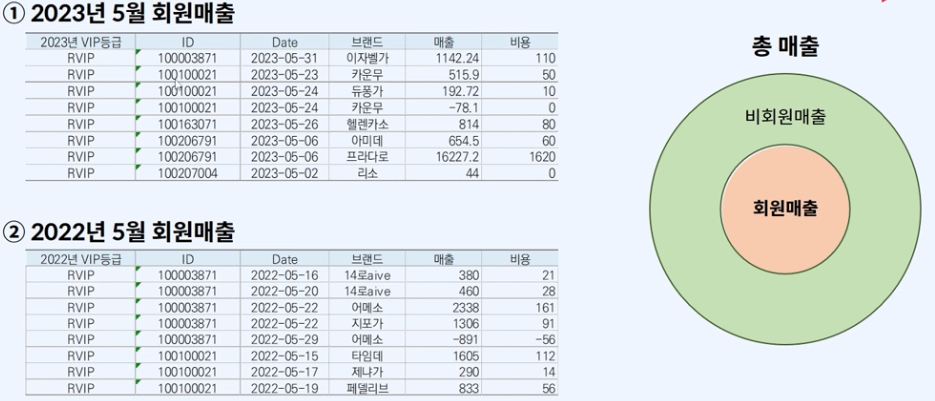
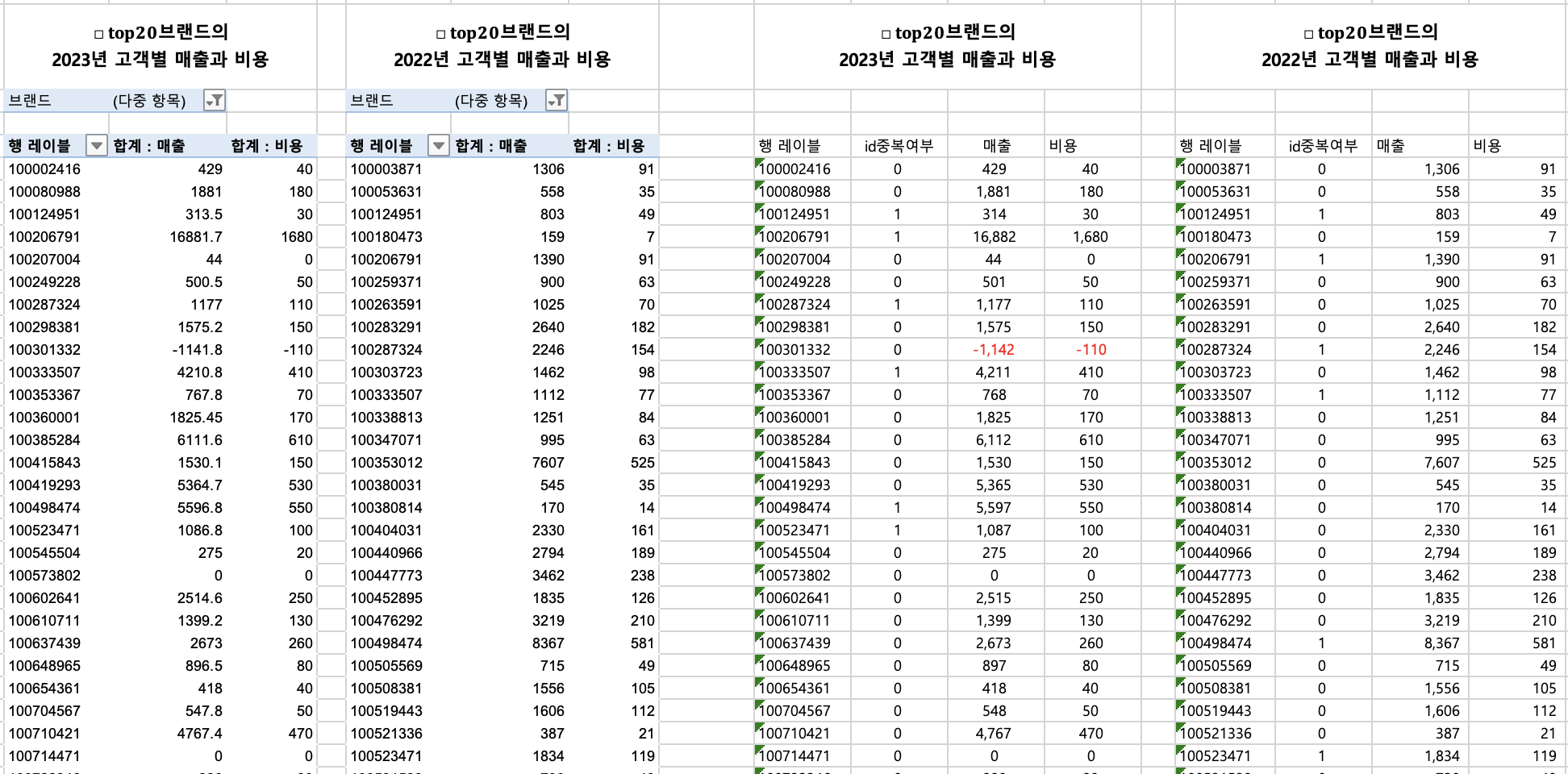
작년도 매출 top20에 대한 2023년 고객별 매출과 비용

2022년 5월 매출에 대한 raw데이터를 피벗테이블로 만들어줍니다. (물론 매출액 관련 숫자화 등 전처리 필요)

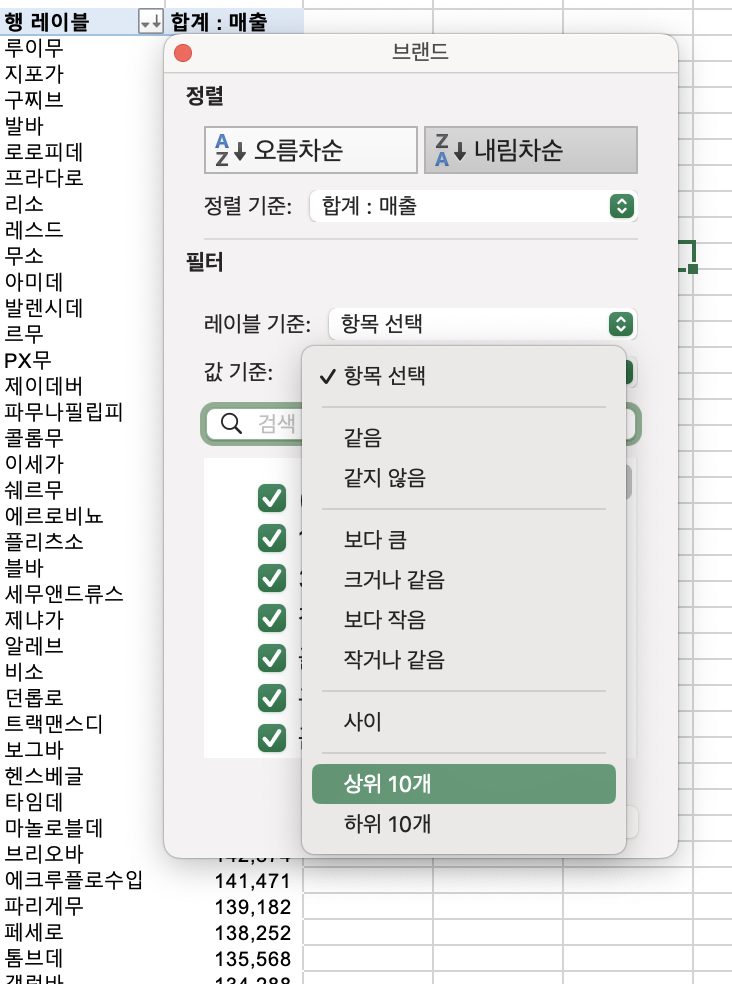
2022년 기준 매출 top20 브랜드 선정

2022년도 매출 raw 데이터

• 행 (브랜드)
• 값 (합계: 매출)
• 셀 서식 : 숫자 -> 1000단위 구분 기호 사용 -> -1,234 로 음수까지
• 행 레이블 오른쪽 클릭 -> 값기준(값필터) -> 상위10개 클릭 -> 20개로 수정

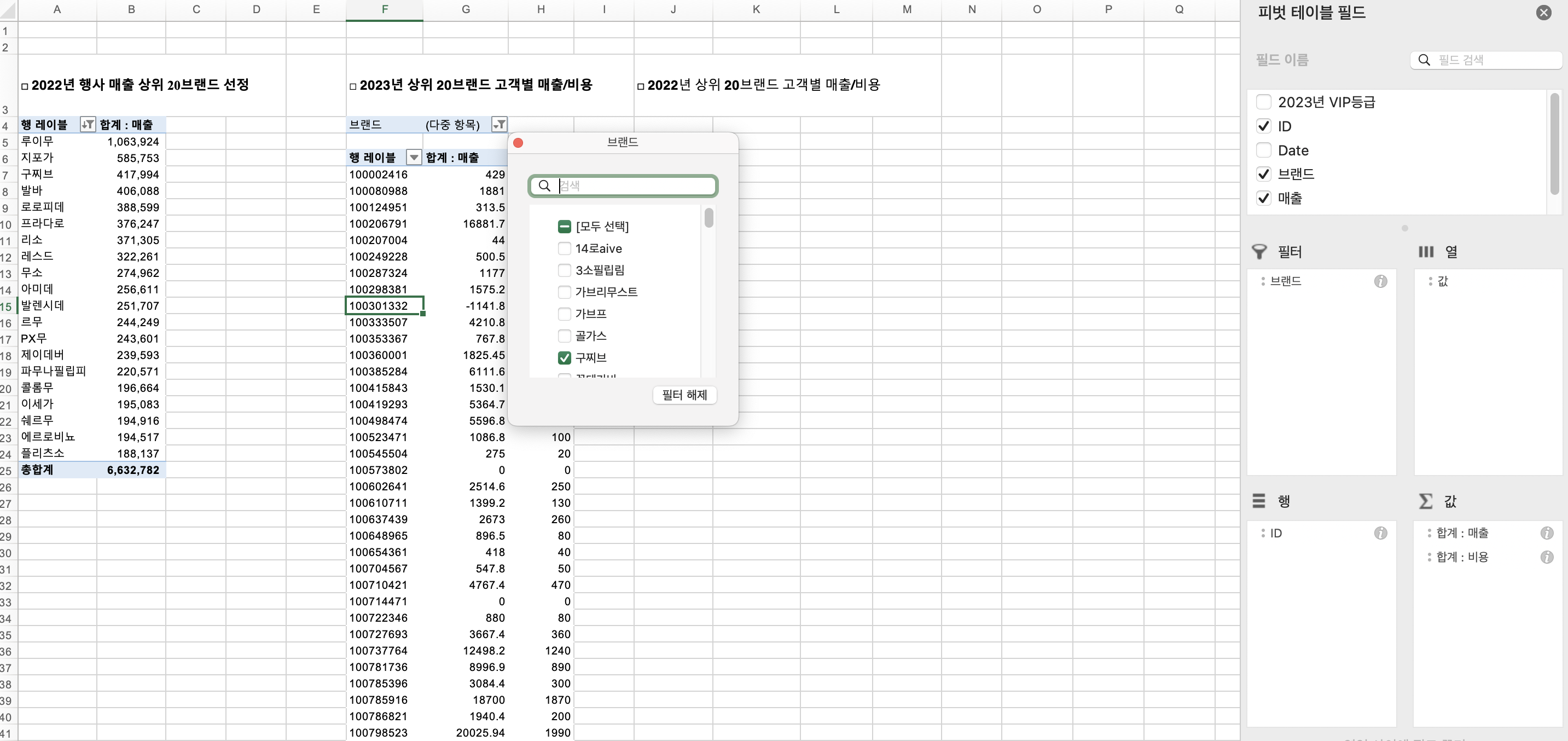
top20 브랜드 올해 고객별 매출과 비용

2023년도 매출 raw 데이터

• 행 (고객 ID)
• 값 (합계 : 매출, 합계: 비용)
• 열 : 값
• 필터 (브랜드) -> 2022년 매출 top20 브랜드를 일일이 지정해줍니다.
  • 안타깝지만 필터에 대해서는 일일이 지정해줘야 합니다.

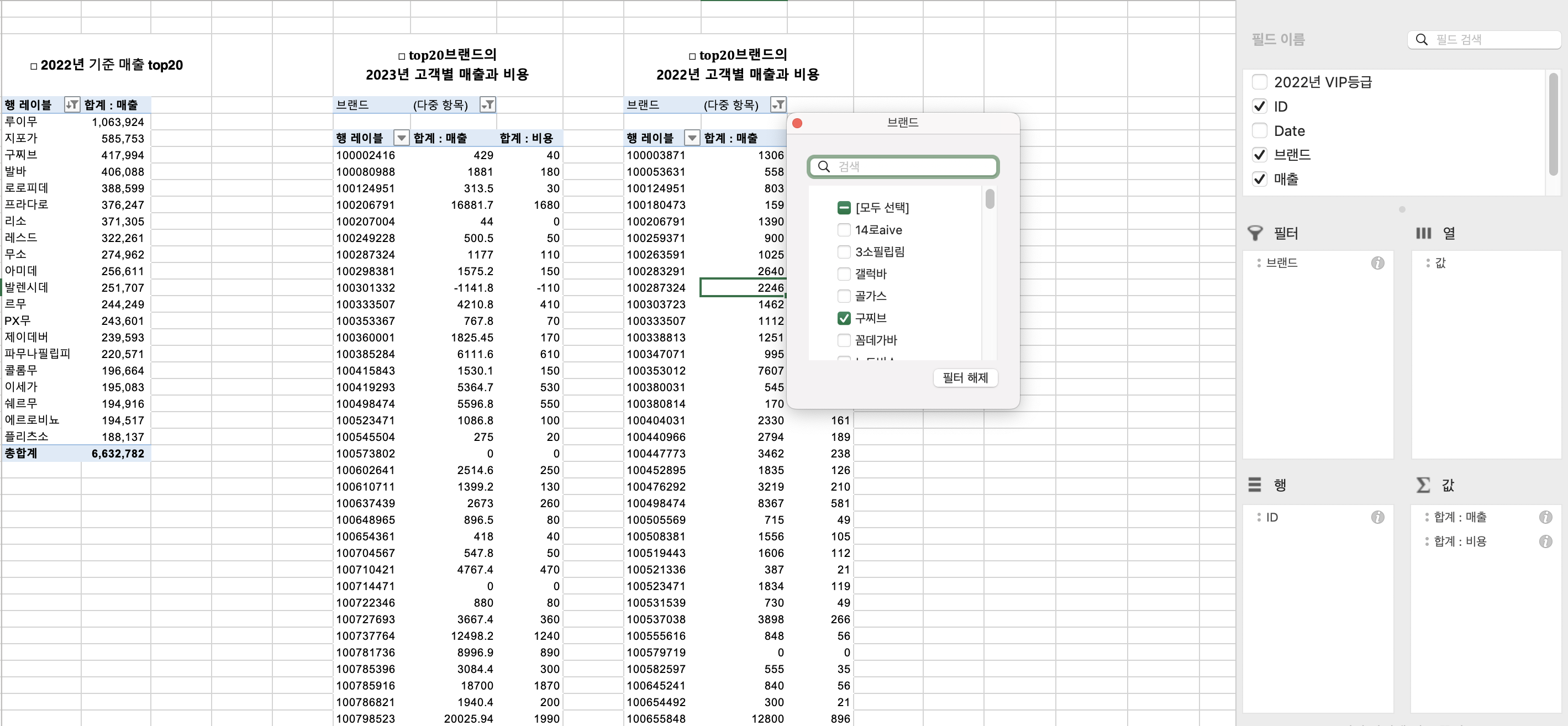
top20 브랜드 작년 고객별 매출과 비용

2022년도 매출 raw 데이터

• 행 (고객 ID)
• 값 (합계 : 매출, 합계: 비용)
• 열 : 값
• 필터 (브랜드) -> 2022년 매출 top20 브랜드를 일일이 지정해줍니다.

작년과 올해 top20브랜드 비교

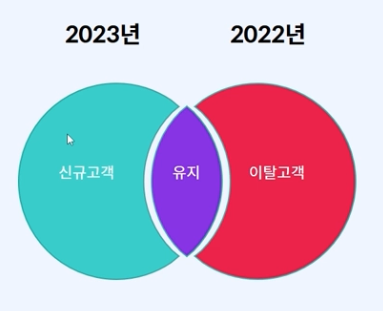
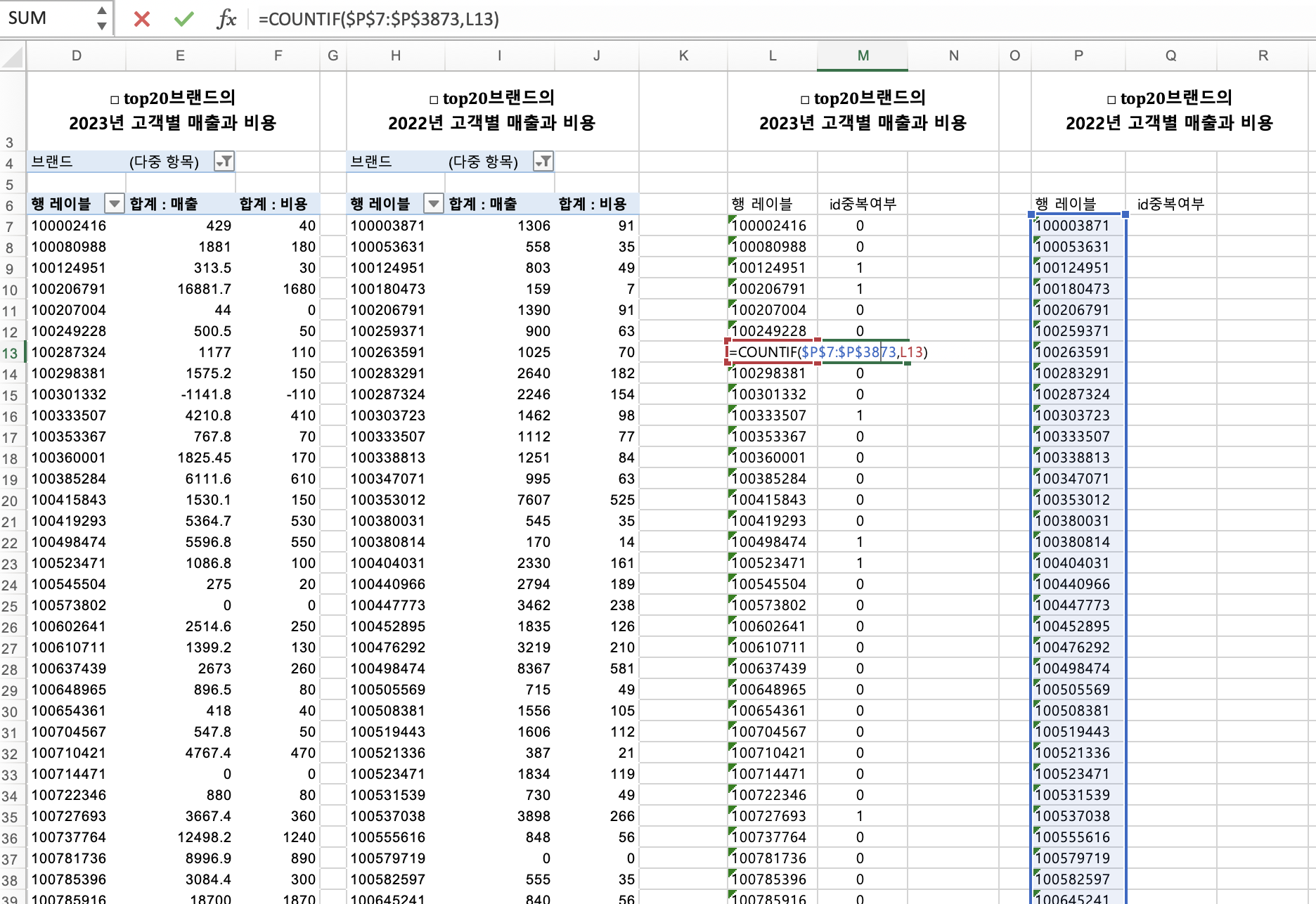
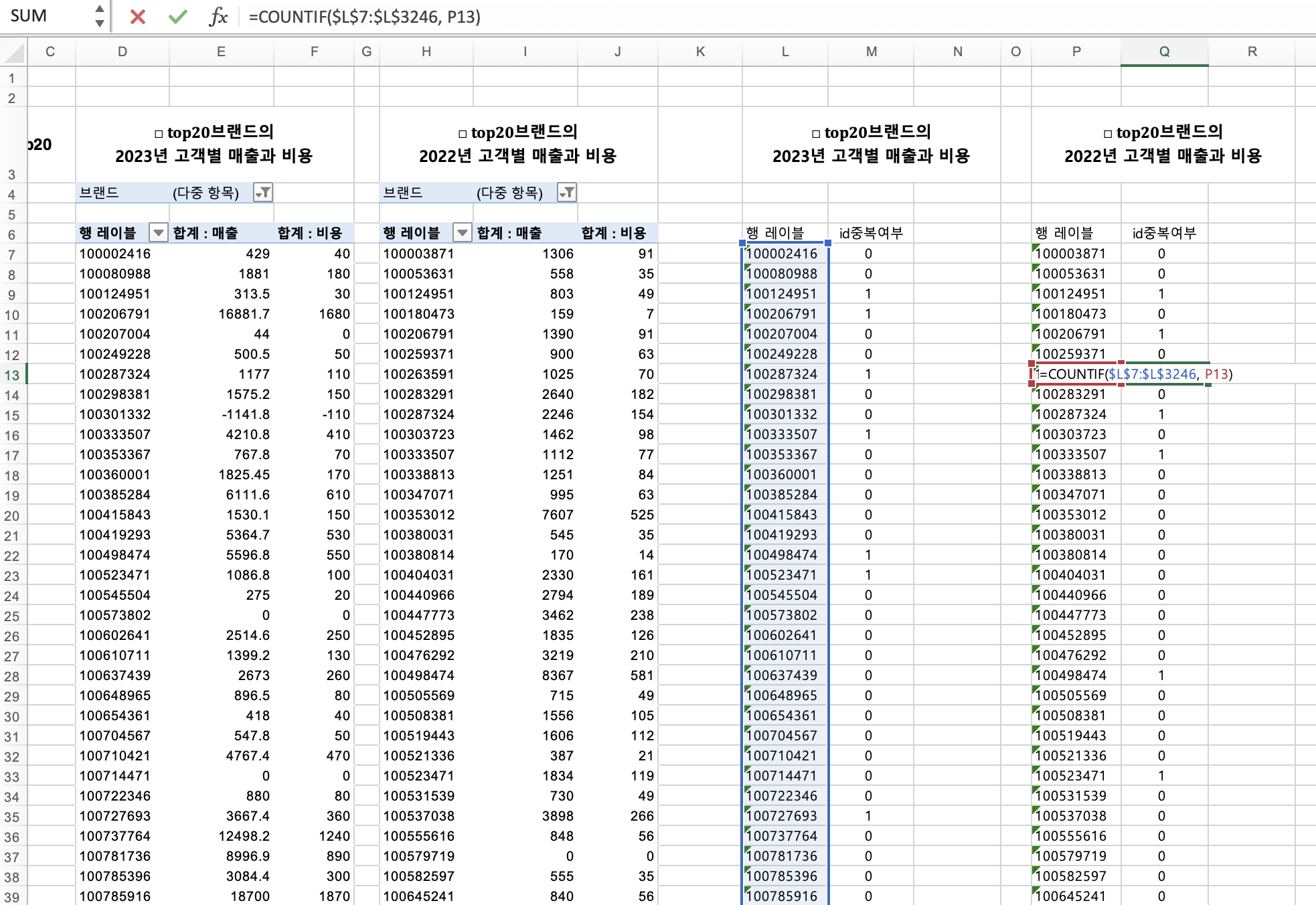
• 동일한 컬럼인 고객 id로 비교할 겁니다.

  • 중복여부 확인
    • 작년에만 있는 고객 : 이탈 고객
    • 올해에만 있는 고객 : 신규 고객
    • 작년과 올해 다 있음 : 유지 고객

• 2023년, 2022년의 고객Id 값 복사 붙혀넣기

• 중복여부 확인하기 위해 =countif(범위, 기준값)
  다만, =countif( $범위$고정 , 값 )
  2023년과 2022년 둘 다 모두 해줍니다.

• 2023년 2022년 각 매출과 비용도 vlookup으로 불러와줍니다.
  =vlookup(찾는값, 범위, 몇번째열에서, False또는0)
  다만, =vlookup($찾는값 , $범위$고정 , 열번호, False또는0

t-test 표본

2023년과 2022년 매출이 얼마나 차이가 나는지 t-test로 검증해줍니다.

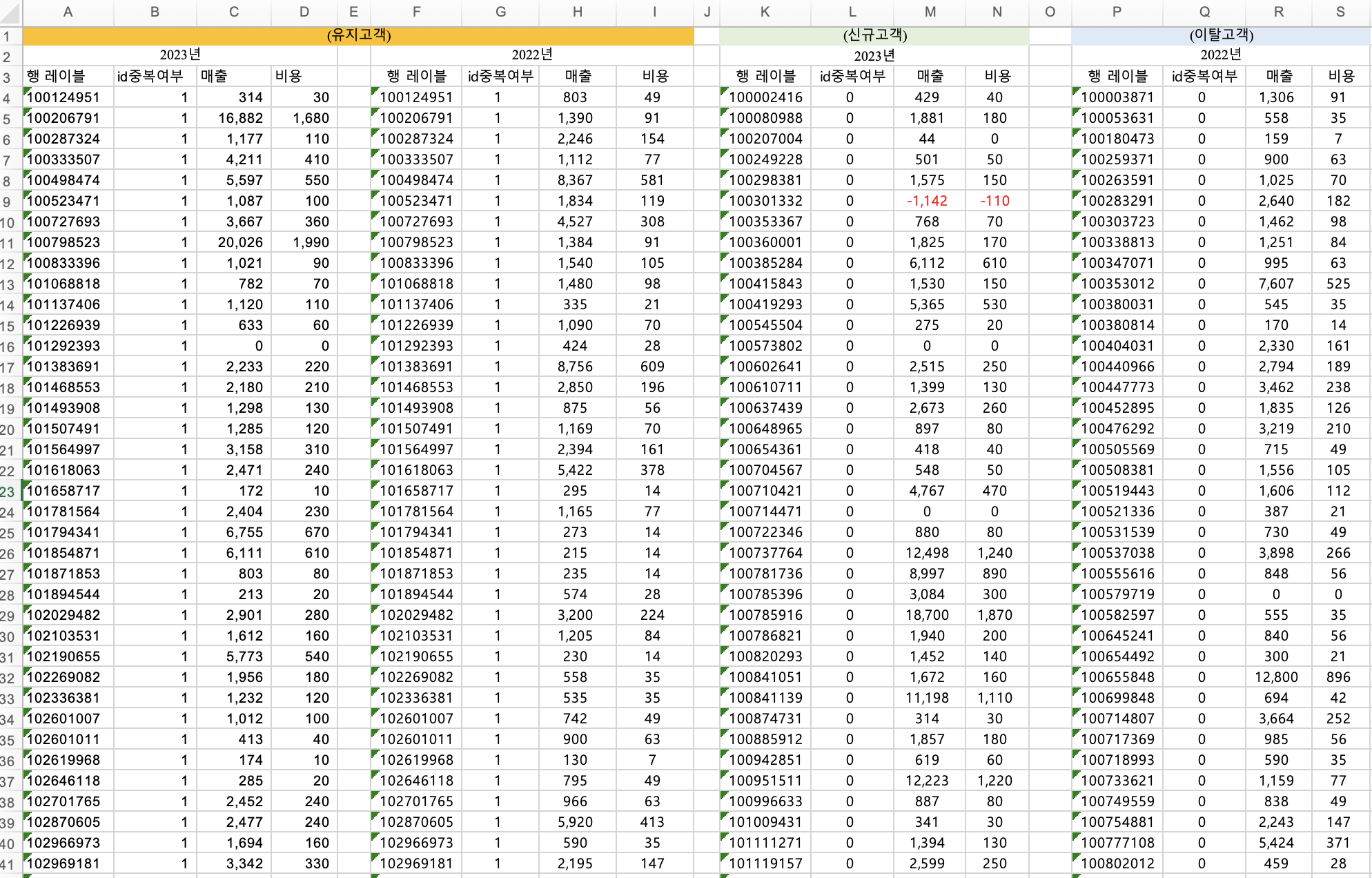
유지고객 (중복고객)

• 각 컬럼명을 필터로 걸어줍니다.
  • 중복여부 :
    • 0은 중복아닌고객
      2023년에는 신규고객, 2022년에는 이탈고객
    • 1은 중복고객
      2023년,2022년 모두 유지 고객
• 2023년, 2022년 모두 각각 중복고객(1)인 데이터만 값 복사 붙혀넣기를 해서 별도 시트에 옮겨줍니다.

tip !
두 데이터의 길이(크기)가 동일하지 않기 때문에
하나의 시트에서 바로 동시에 필터를 걸면 안먹힙니다.
귀찮더라도, 하나하나씩 값복사붙혀넣기로 새 시트에 예쁘게 넣어서 옮겨주면서 작업해줍니다.

• 2022년과 2023년 각각 유지고객(중복여부가 1) 수가 동일합니다.
  즉, 표본의 갯수가 동일합니다.

신규고객 (2023년에만)

• 2023년에만 있고, 2022년에는 없는 신규 고객만 추출
  2023년 데이터에서 중복여부가 없는 신규고객 (중복여부가 0) 에 한하여 값 복사 붙혀넣기 해줍니다.

이탈고객 (2022년에만)

• 2022년에만 있고, 2023년에는 없는 이탈 고객만 추출
  2022년 데이터에서 중복여부가 없는 이탈고객
  (중복여부가 0) 에 한하여 값 복사 붙혀넣기 해줍니다.

t-검정 종류

데이터 > 데이터분석 클릭

• t-검정 : 쌍체비교 : 동일한 개체 또는 단위에 대한 두 관측치 집단 간의 차이를 비교 = 두 집단의 전/후 비교 (두 집단의 평균 차이를 검정)
  t-Test: Paired Two Sample for Means

• t-검정 : 등분산 가정 두집단 : 두 집단의 분산이 서로 동일하다고 가정 (두 집단의 평균 차이를 검정)
  t-Test: Two-Sample Assuming Equal Variances

• t-검정 : 이분산 가정 두집단 : 두 집단의 분산이 서로 다르다고 가정 (두 집단의 평균 차이를 검정)
  t-Test: Two-Sample Assuming Unequal Variances

  Variable 1 Range : 변수 1 범위
  Variable 2 Range : 변수 2 범위
  Alph : 유의수준

통계량 해석

• Mean 평균
• Variance 분산
• Observations 관측수 : 표본의 수
• Pearson Correlation 피어슨 상관 계수 : A가 늘 때, B가 얼만큼 느는가 하는 공변성을 나타내는 값이며,
  1 = 양의 상관계수 (A와 B가 동시에 증가한다)
  -1 = 음의 상관계수 (A가 증가하면, B는 반대로 감소한다)
• Hypothesized Mean Difference 가설 평균 차
• df 자유도 : 관측수 -1
• t Stat t통계량
• P(T<=t) one-tail P(T<=t) 단측 검정
• t Critical one-tailt 기각치 단측 검정
• P(T<=t) two-tail P(T<=t) 양측 검정
• t Critical two-tail t 기각치 양측 검정

통계량에 대해 셀서식으로 보기 편하게 설정하겠습니다. (1000단위 , 표시 등)

유지고객 t-test(쌍체비교)

유지고객에 대해 쌍체비교를 진행하겠습니다.

매출에 대해서

• 변수1입력범위는 2023년의 '매출' 컬럼전체
• 변수2입력범위는 2022년의 '매출' 컬럼전체

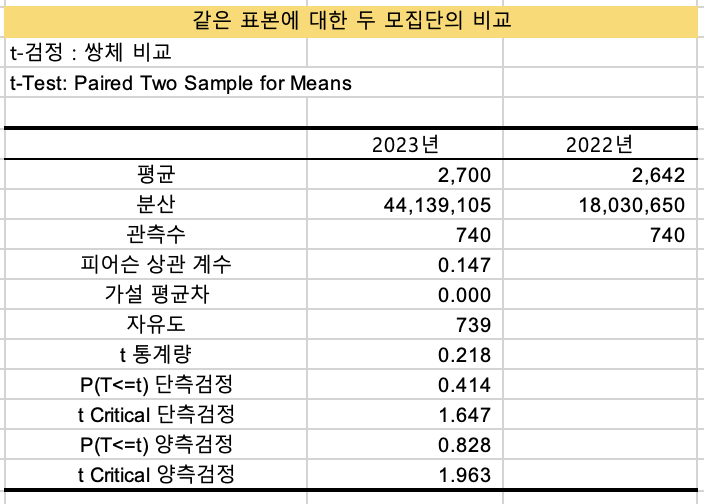
t-검정:쌍체비교 결과에 대해 확인해보겠습니다.

• 평균 : 2023년의 고객1인당 평균 매출액이 +60 올랐습니다.
• 분산 : 2023년이 훨씬 큽니다.
• 관측수 : 같은 대상(표본)을 비교했기 때문에 동일합니다.

t통계량인 t-value값보단 p-value값을 보아서, 우연히 2023년 매출이 더 높은것인지 아닌지 확인해야 합니다.

단측검정? 양측검정?

• 단측검정 : 높은지 낮은지 비교
  2023년 고객 평균 매출이 2022년보다 크다
• 양측검정 : 같은지 다른지 비교
  2023년과 2022년 유지고객의 평균은 같은가 다른가

참고로 가설은 2023년과 2022년 유지고객의 평균은 같은가 다른가 이기 때문에 양측검정 값을 보겠습니다.

물론 둘 다 볼 수 있습니다.

P 단측검정과 P 양측검정 모두 0.05 보다 훨씬 큰 값을 가지고 있습니다.

따라서, 2023년 매출이 더 높은 것에 대해 2022년과 달리 홍보 등에 더 신경을 쓴 것과는 상관없다는 (무의미한 = 우연히 나온) 결과가 나왔습니다.

비용에 대해서

• 변수1입력범위는 2023년의 '비용' 컬럼전체
• 변수2입력범위는 2022년의 '비용' 컬럼전체

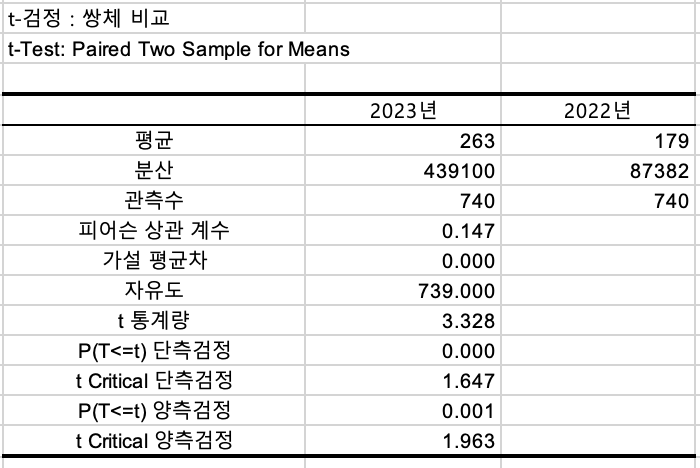
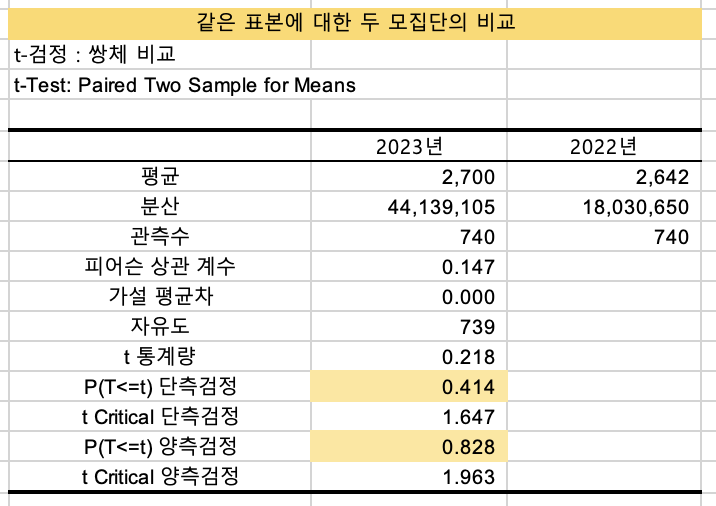
평균도 2023년이 많이 증가했습니다.
중요한건 t통계량과 p값입니다.

매출에 대해 t검정을 했을 때보다 t값과 p값이 다릅니다.

특히, 두 개의 p값이 0.05보다 훨씬 적습니다 = 유의미한 결과 = 두 모집단 차이가 나는데 있어서, 우연이 아니다

따라서, 비용에 대해서는 2023년이 2022년과 다르다
= 2023년이 훨씬 크다
= 2022년에 비해, 2023년 비용에 대한 고객 평균금액이 증가했다!

신규와 이탈고객에 대한 F-Test(등분산성)

t-test와 방식(표본을 가지고 평균 비교)와 비슷합니다.

데이터 > 데이터분석 클릭
F-Test Tow-Sample for Variances F-검정 : 분산에 대한 두 집단 을 클릭해서
두 집단이 등분산인가 아닌가 확인해주겠습니다.

등분산?

등분산이란, 두 개 이상의 집단이나 변수의 분산이 서로 비슷하다는 의미입니다.
즉, 각 집단 또는 변수의 데이터들이 흩어진 정도가 유사한지 아닌지 확인해보겠습니다.

매출에 대해서

• 변수1입력범위는 2023년의 '매출' 컬럼전체
• 변수2입력범위는 2022년의 '매출' 컬럼전체

F-검정 (F-Test Two-Sample for Variances)를 진행해줍니다.

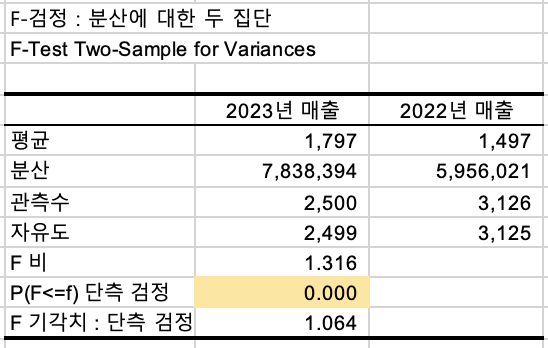
p-value값이 0.05보다 작은 0.000 으로 나와,
두 집단의 분산이 다르다 라고 결론이 나왔기 떄문에
T-Test 검정을 진행해줍니다.

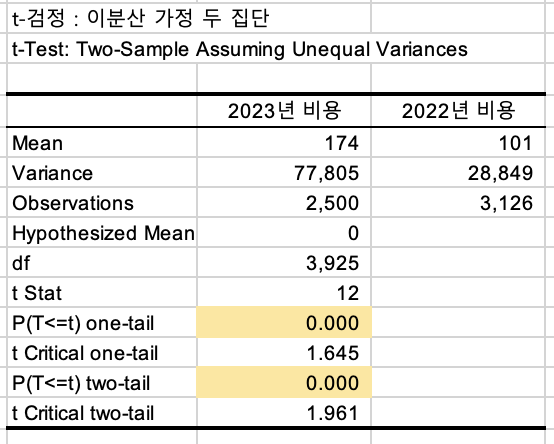
신규와 이탈고객에 대한 t-test(이분산 가정)

데이터 > 데이터분석 클릭
t-검정 : 이분산 가정 두집단 을 진행해주겠습니다.

: 두 집단의 분산이 서로 다르다고 가정 (두 집단의 평균 차이를 검정)
t-Test: Two-Sample Assuming Unequal Variances

매출에 대해서

2023년 신규고객과 2022년 이탈고객의 '매출'을 비교해보겠습니다.

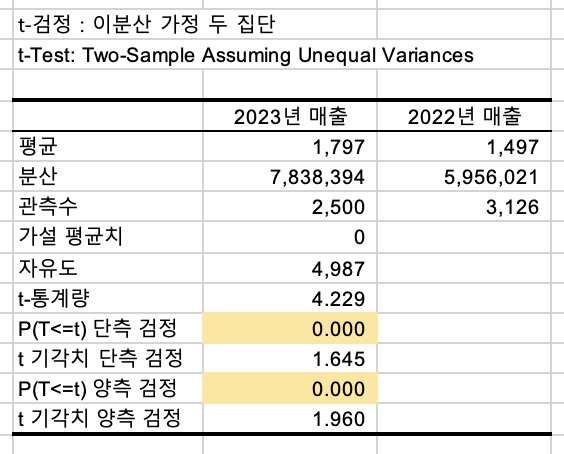
매출은 많이 늘었습니다.
t 통계량도 많이 늘었습니다.
p-value값에 대해서도 단측검정, 양측검정 모두 0.05보다 더 작습니다.

즉, 독립표본(신규, 이탈) 모집단의 고객당 매출평균은 다르다.
또한 신규 고객의 고객당 매출평균은 커졌습니다!

비용에 대해서

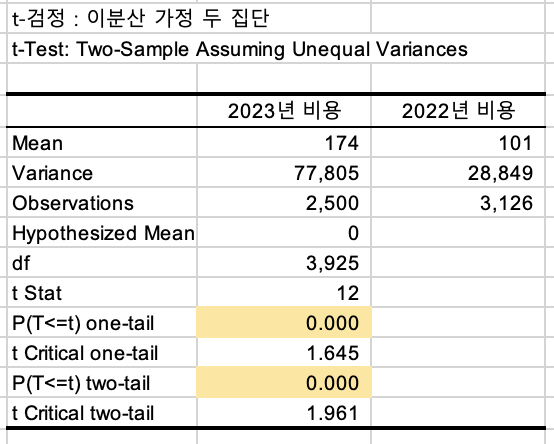
t통계량도 매우 높습니다.
비용에 대한 평균도 2023년이 매우 증가했습니다.
p-value값에 대해서도 단측검정, 양측검정 모두 0.05보다 더 작습니다.

즉, 독립표본(신규,이탈) 모집단의 고객당 비용 평균은 다르다.
또한 신규 고객의 고객당 비용 평균은 커졌습니다!

최종 결과

2022년 작년과 2023년 올해 기준, 백화점 고객들 대상으로
2023년 추가된 행사가 비용은 많이 썼지만, 매출은 모집단 통계를 추정했을 때 의미가 없음 확인됩니다.

2023년 신규 고객과 이탈고객 대상으로
독립표본 T테스트를 진행했을 때는, 매출 증가가 확인됩니다.
하지만 비용에 대한 증가가 더 커졌습니다.

통계적 차이로 보았을 때, 매출 증가 및 비용 증가에 대해서는 우연히 일어난 것이 아닙니다.

쉽게 정리하자면
작년보다 행사 비용이 더 많이 증가된 만큼이나 백화점 매출 증가는 미미합니다.