데이터 탐색

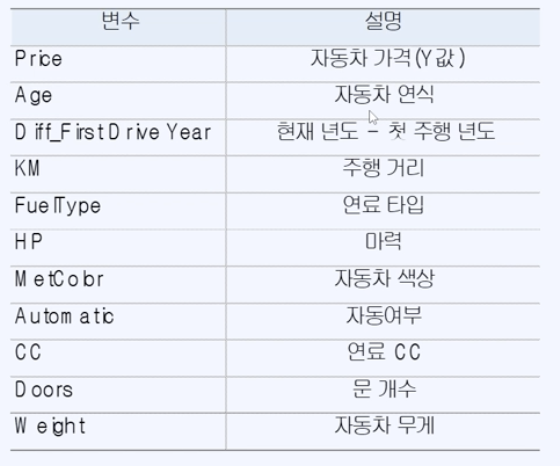
구해야하는 y = Price 가격
price 자동차 가격 데이터 분포를 먼저 확인해두겠습니다.

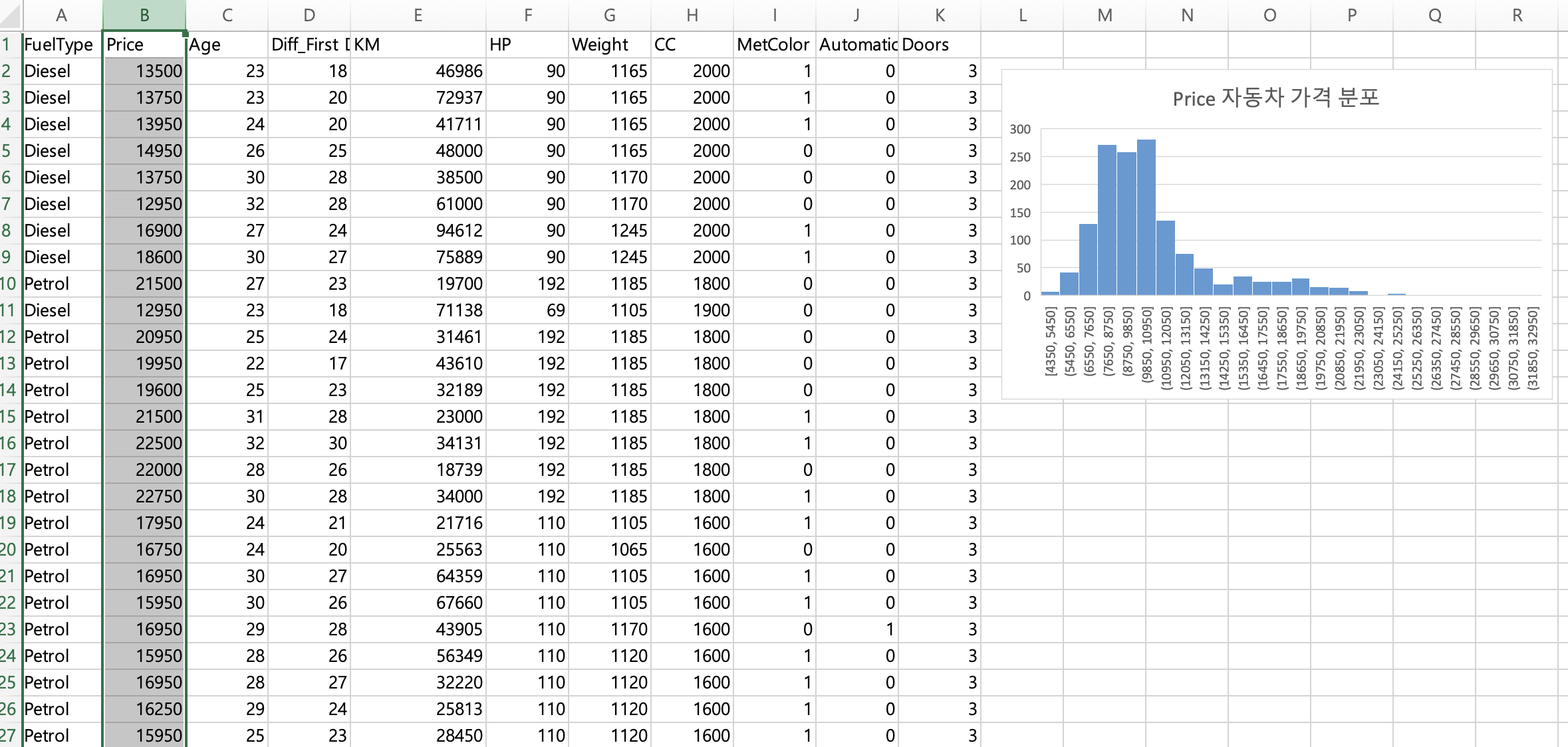
Age (자동차 연식)과 Diff_FirstDriceYear (첫주행으로부터 년도)은 다소 비슷할 것 같은데, 얼만큼 차이가 나는지 비교도 하겠습니다.

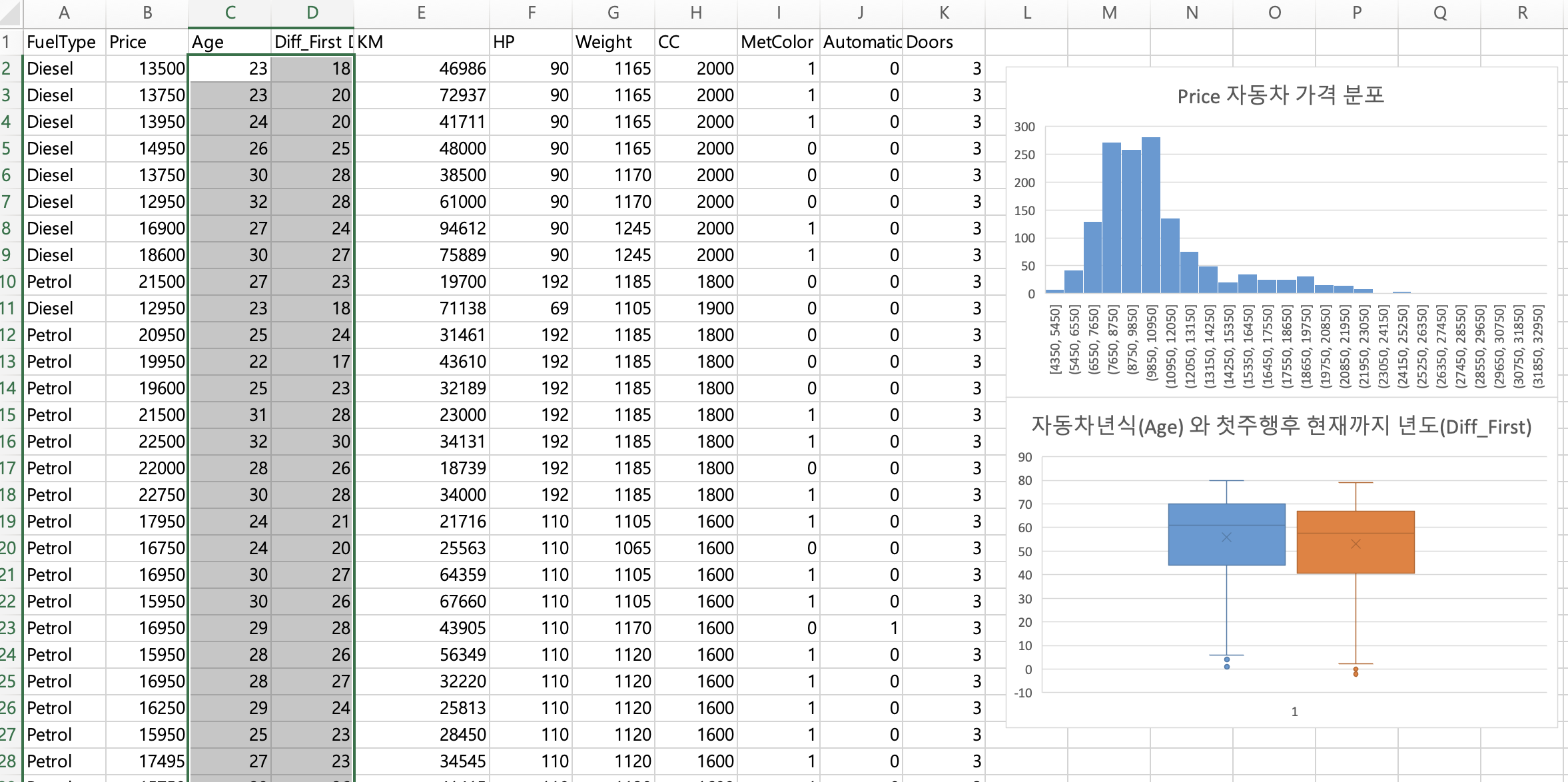
역시나 비슷한 것 같습니다.

상관분석(다중공선성 확인)

데이터 > 데이터분석 > Correlation 상관분석 >

홈 > 조건부서식 > 새규칙 > 색상 설정

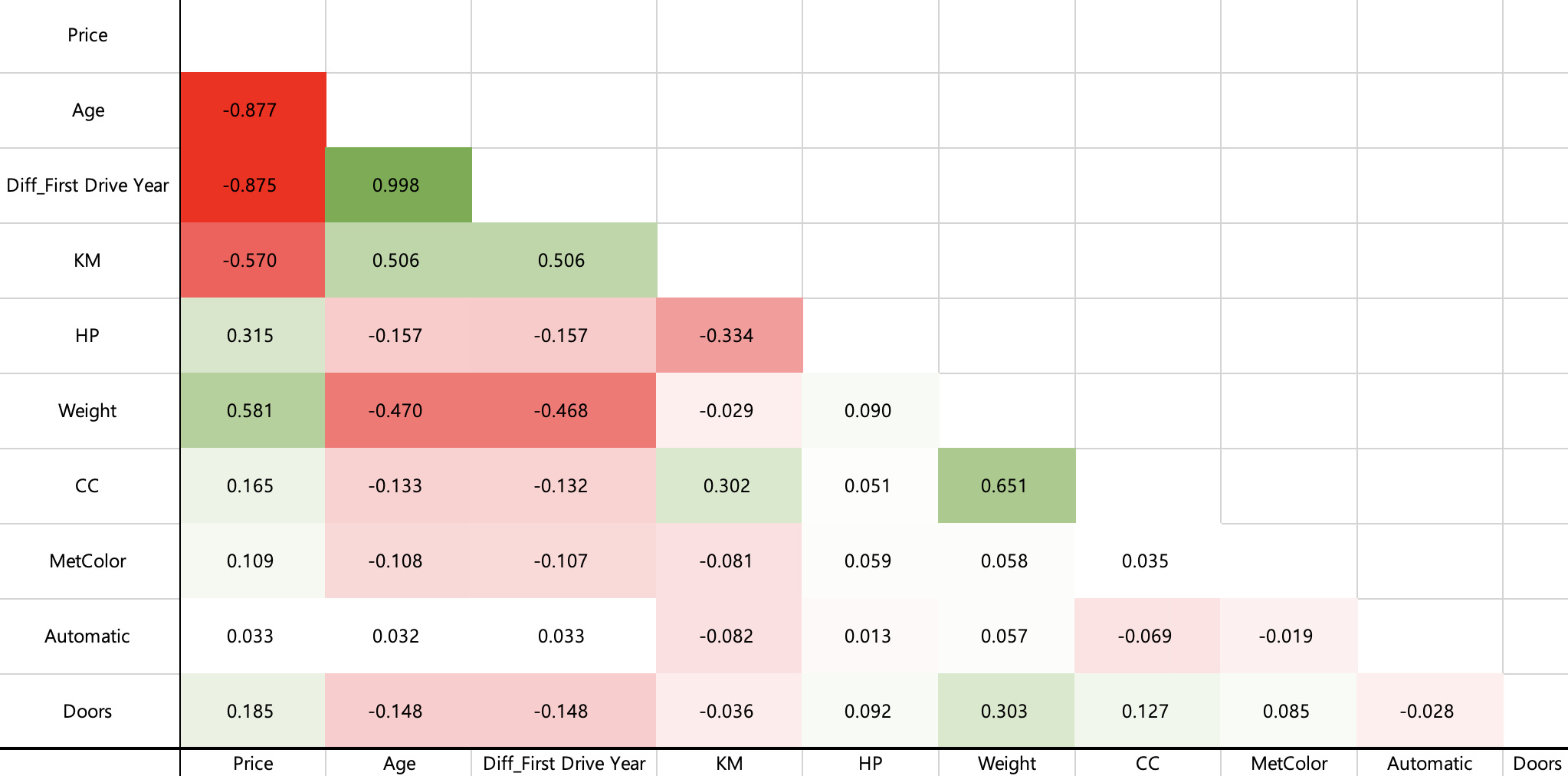
Price(y)와 큰 상관관계를 가진 x피쳐들을 확인해보겠습니다.

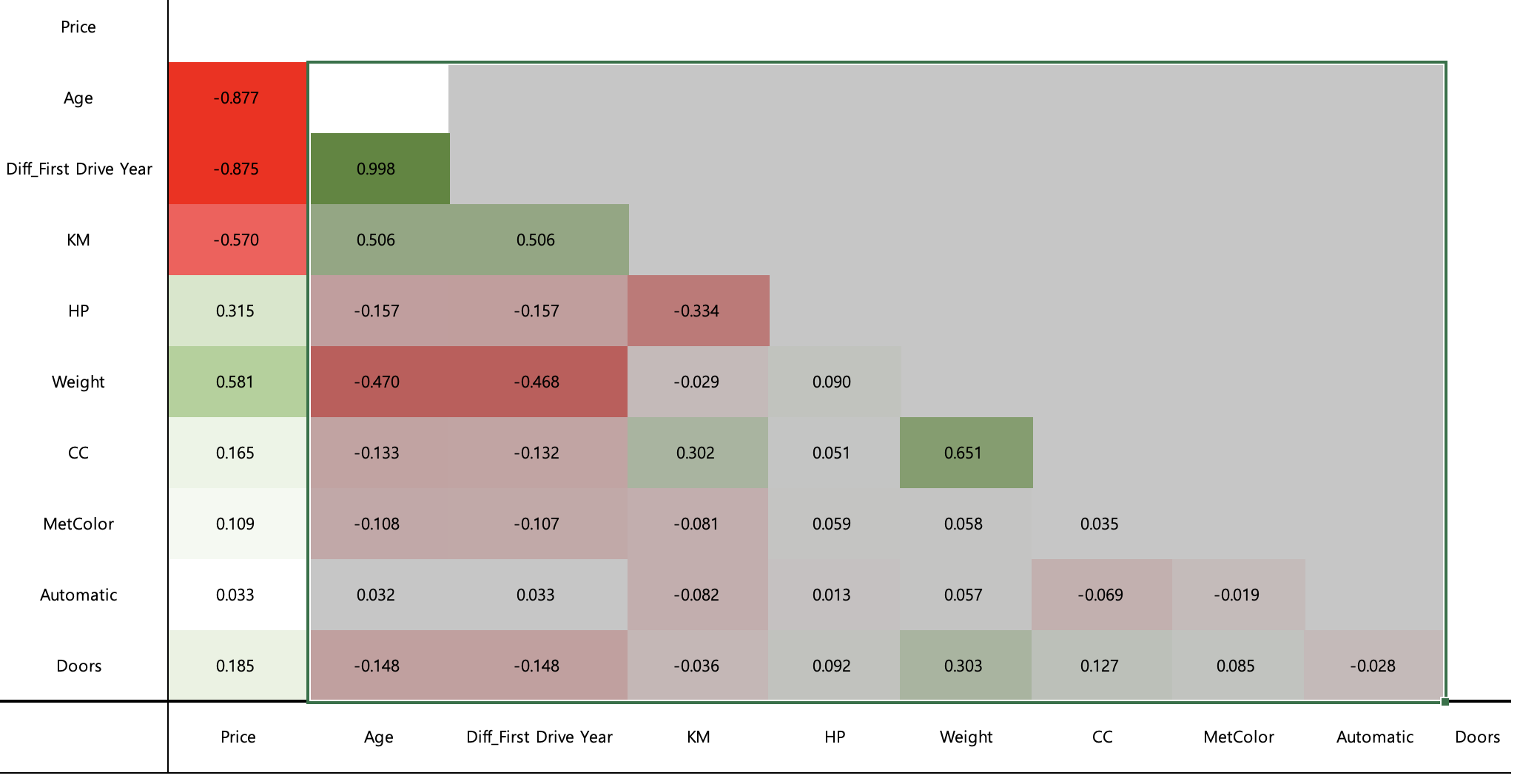
• 양의 상관관계 중에선 Weight
• 음의 상관관계 중에선 Age, Diff_First Drive Year, KM 으로 보여집니다.

x들끼리의 큰 상관관계를 가졌는지도 집중해서 보겠습니다.
Price(y)를 제외하고 서로 상관관계여부를 본다면, Age와 Diff_First Drive Year 간의 양의 상관관계가 0.998로서 매우 1에 높게 나왔습니다.
두 x의 상관성이 매우 높기 때문에, 이대로 회귀분석을 진행하게 될 경우 음/양이 반대로 잘못 나올 가능성이 큽니다.

둘 중 하나를 제거하겠습니다. (Diff_First Drive Year 피쳐 제거)

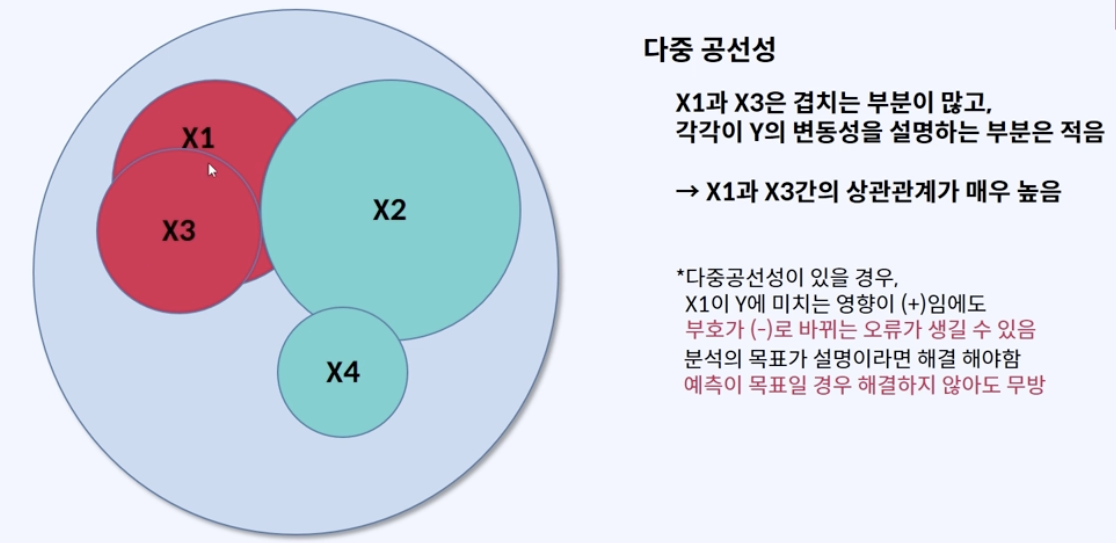
다중공선성 (Multicollinearity)

Features(x) 간의 상관관계가 높으면, y의 미치는 영향이 달라질 수 있습니다.
그래서 미리 Features(x)간의 상관관계가 있는지 확인해줘야 합니다.

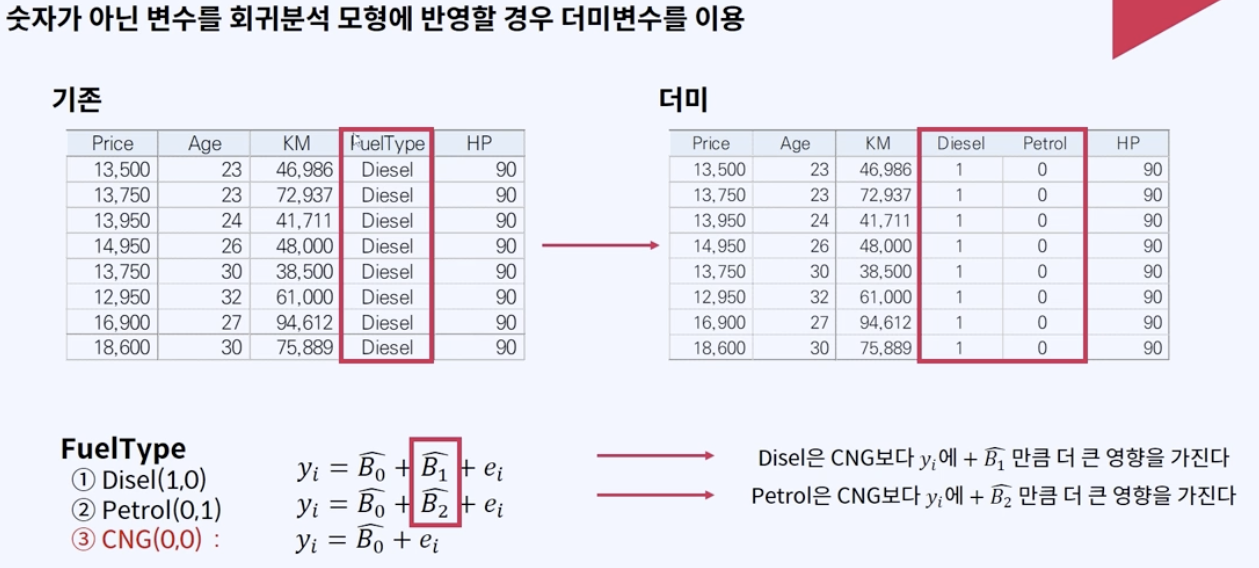
문자형->수치형 변경(가변수)

회귀분석에 앞서, 문자형 피쳐를 수치형으로 변경해주겠습니다.
FuelType 피쳐에는 데이터 종류가 총 2가지 있습니다.
Diesel는 1로,
Petrol는 0로 변경해주겠습니다.

=if(해당 셀이 Diesel이라면, 1 , 아니라면 0) 
=IF($A2=$B$1,1,0)

가변수 (Dummy Variable)

수치가 아닌 문자형(카테고리형) 변수를 더미변수로 수치화 합니다.

회귀분석

데이터 > 데이터분석 > Regression 회귀 분석
y축 : price 자동차 금액
x축 : price 제외한 나머지

95% 신뢰구간
label 컬럼명 포함

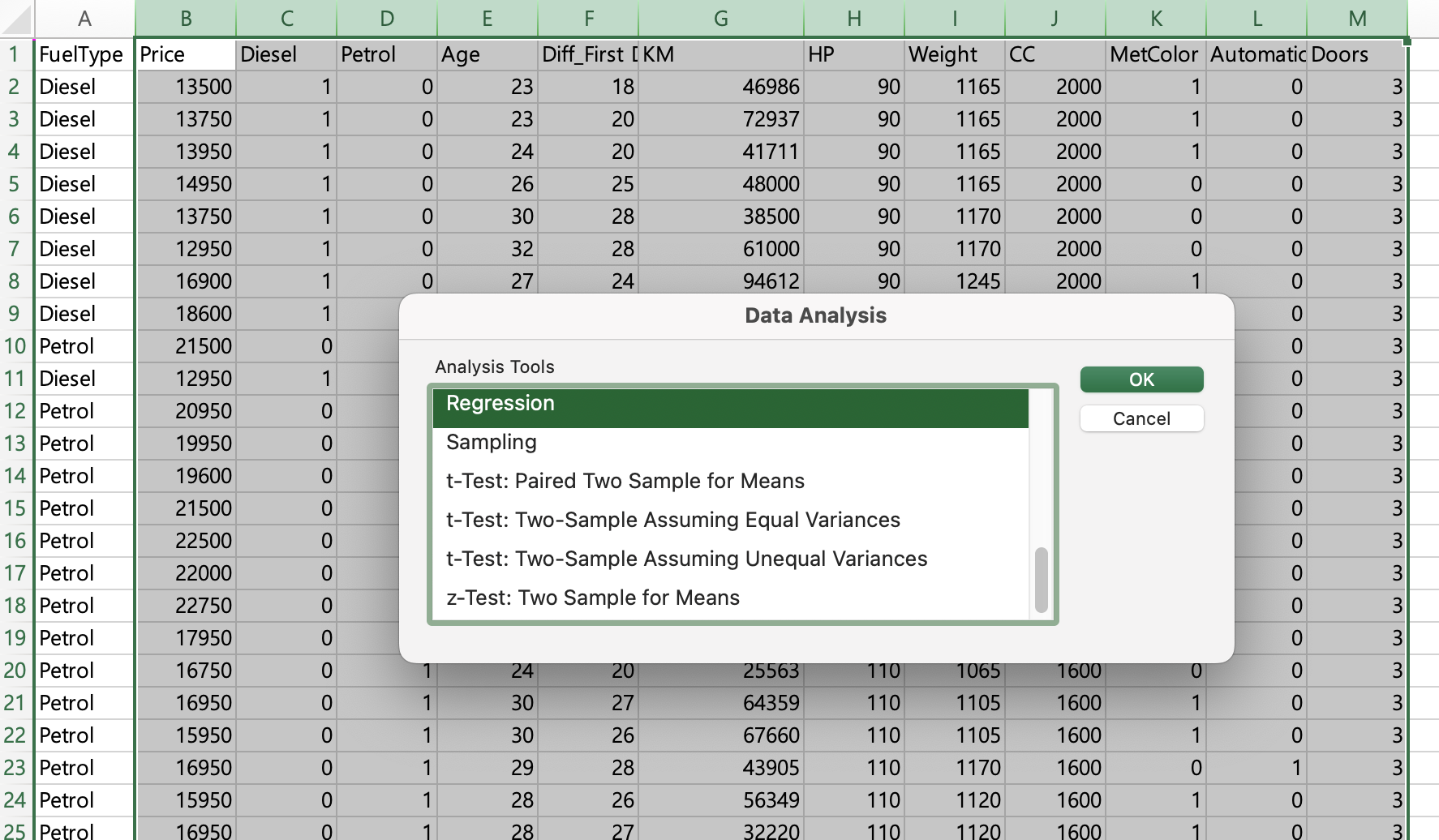
회귀분석 결과를 보기 좋게 변경합니다.

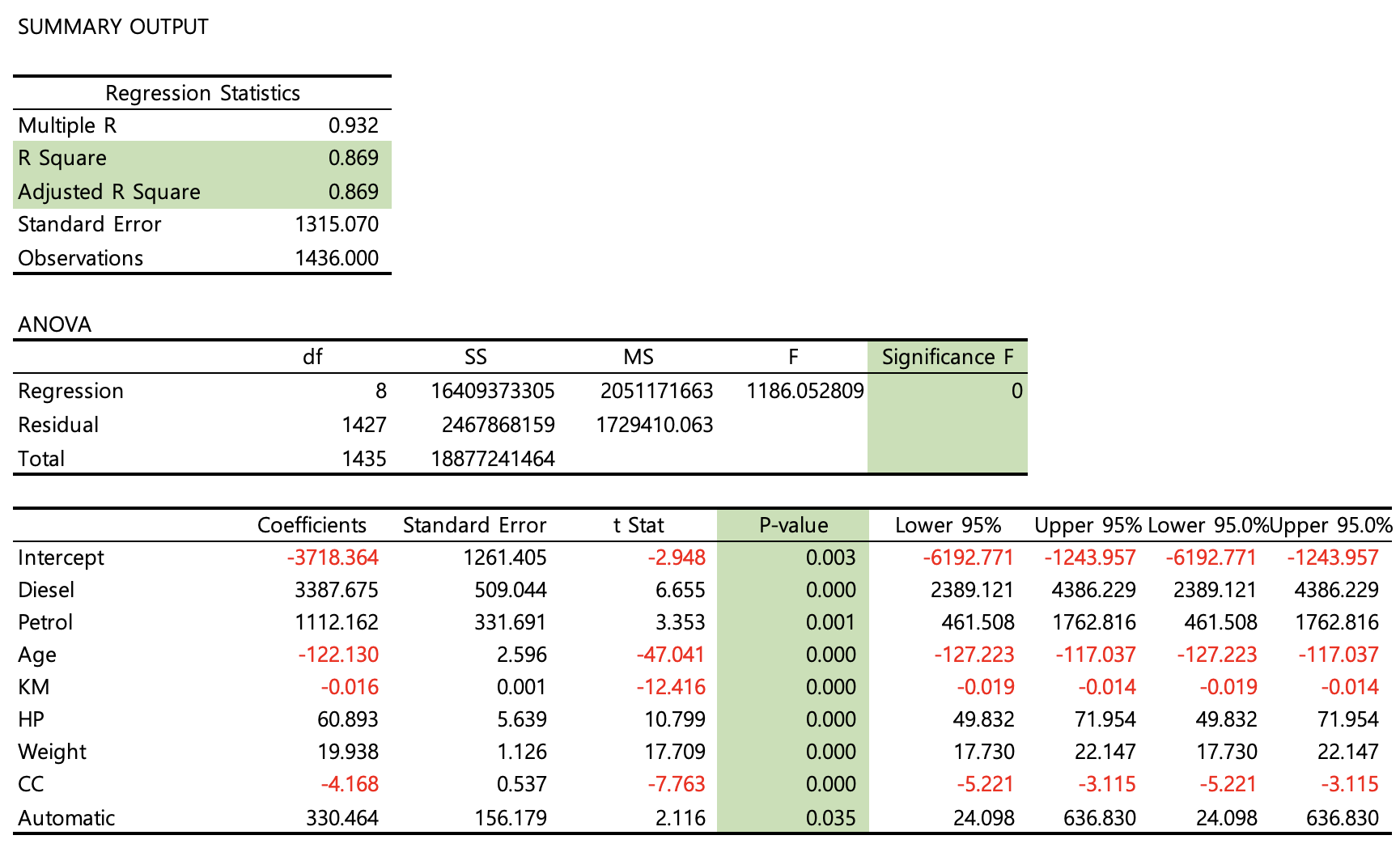
회귀분석 결과

Multiple R 다중 상관계수
R Square 결정계수
Adjusted R Square 조작된 결정계수 (백분율 %의 설명력을 가짐)
Standard Error 표준 오차
Observations 견측수
Regression 회귀
Residual 잔차
Intercept y절편
Coefficients 계수
Standard Error 표준오차
t Stat t통계량
P-value p값
Lower 95% 하위95%
Upper 95% 상위95%
Lower 95.0%
Upper 95.0%

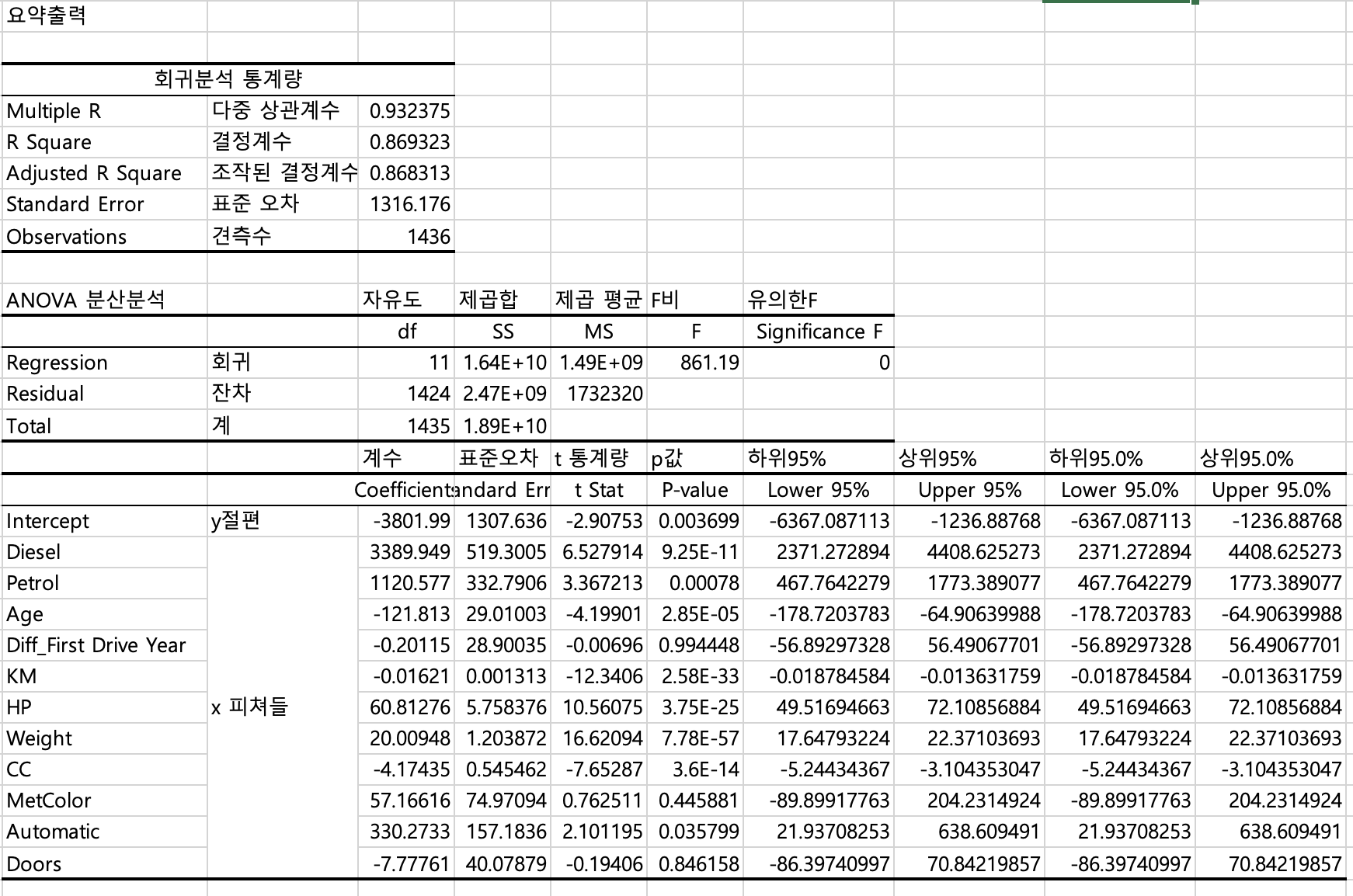
조작된 결정계수는 설명력을 뜻합니다. 즉 약 86%의 설명력을 가지는 회귀분석 결과가 나왔습니다.
보통 80% 이상인 경우 좋은 수치로 여겨집니다.

유의한F가 0.05보다 작아야, 해당 분석은 의미가 있는 분석입니다.
(0.05보다 크면 우연히 발생한 것으로 별 의미 없는 분석이란 뜻)

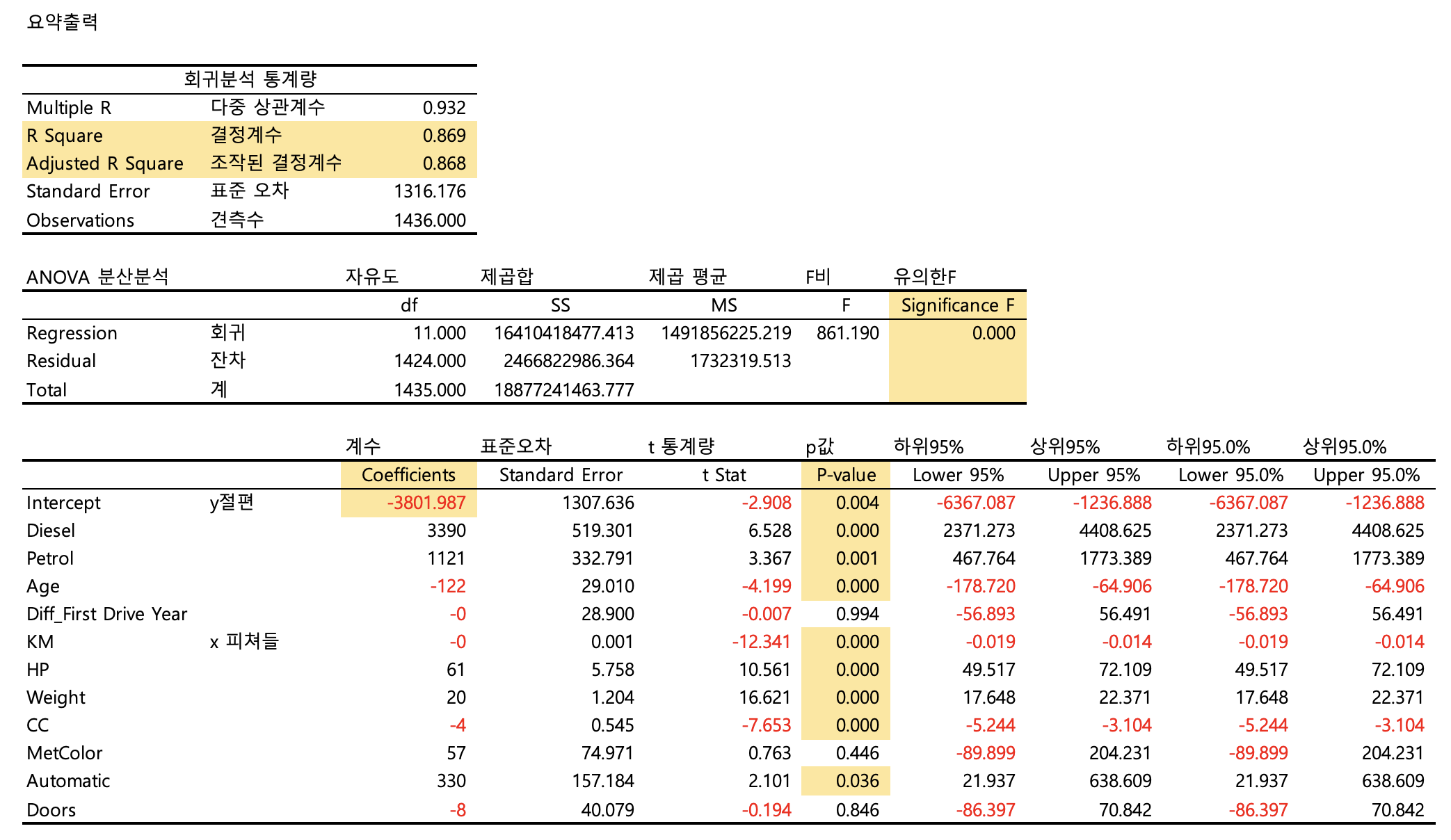
y절편에 따른 x변수들의 계수를 보면
Diesel이 가장 높은 영향력을 미치는 변수이며, Age 자동차의 연식(x)인 경우 감소할 수록, Price 자동차의 가격(y)가 증가합니다.

각 x변수들의 p벨류값을 보시면, 0.05보다 큰 값들은 우연히 발생한 것으로 의미가 없는 변수이기에, 제거 하는게 좋겠습니다.

회귀분석 개선

• p벨류값이 0.05보다 큰 x변수( Diff_first Dive Year와 MetColor, Doors) 제거

다시 실행해보았는데, 사실 이전보다 크게 개선되지는 않았습니다.

예측값 구하기

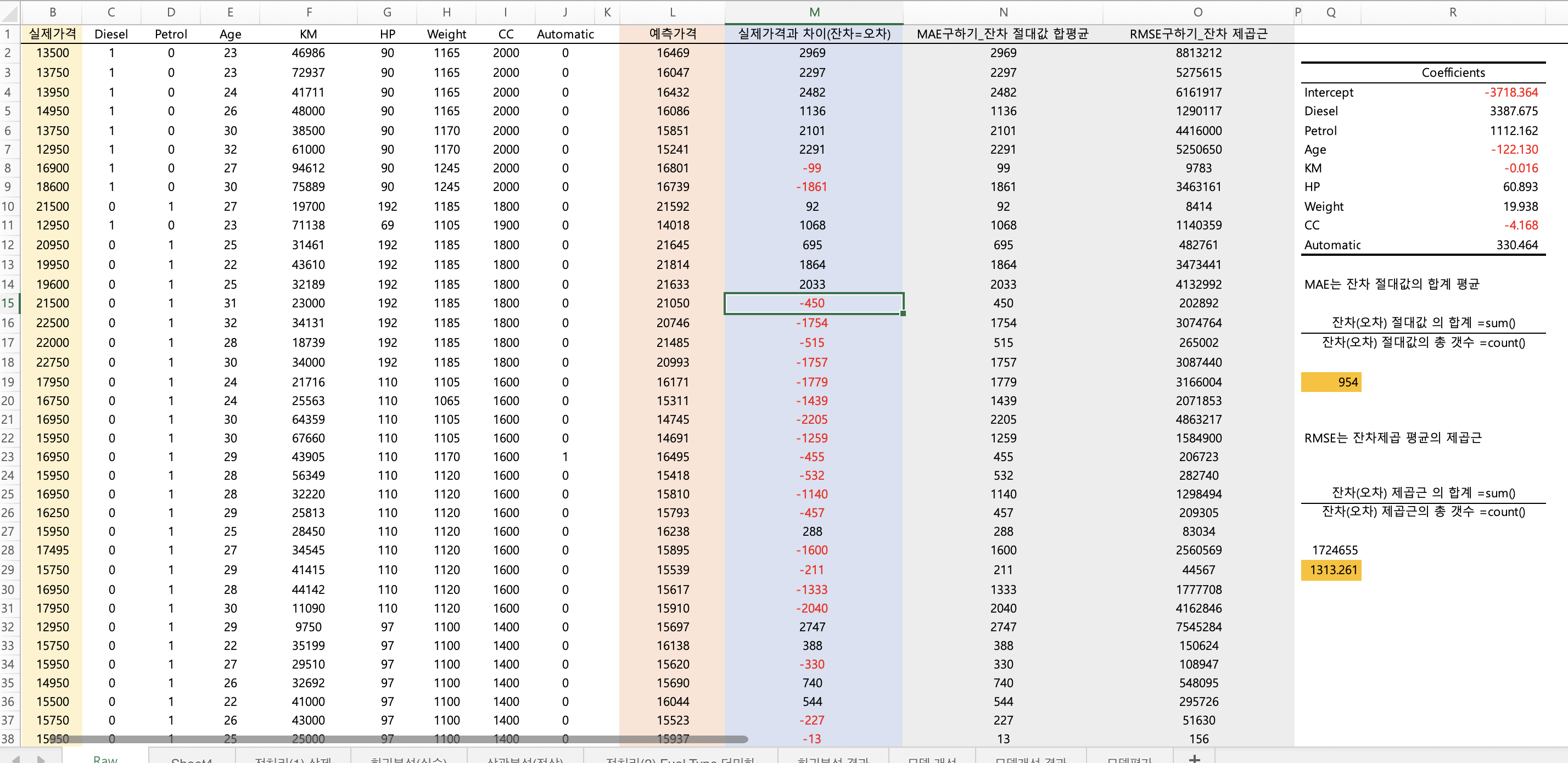
구한 회귀계수로 예측값 (중고차 예측금액)을 구합니다.

y 절편값 
+ (1번 변수의 회귀계수 coef * 1번 변수의 실제값 )
+ (2번 변수의 회귀계수 coef * 2번 변수의 실제값 )
+ (3번 변수의 회귀계수 coef * 3번 변수의 실제값 )
.... 

• 회귀계수 coef 값은 모두 절대참조 $ 를 두 번 해줍니다.

• 이렇게 구한 예측가격과 실제가격의 차이 (잔차) 또한 구해줍니다.

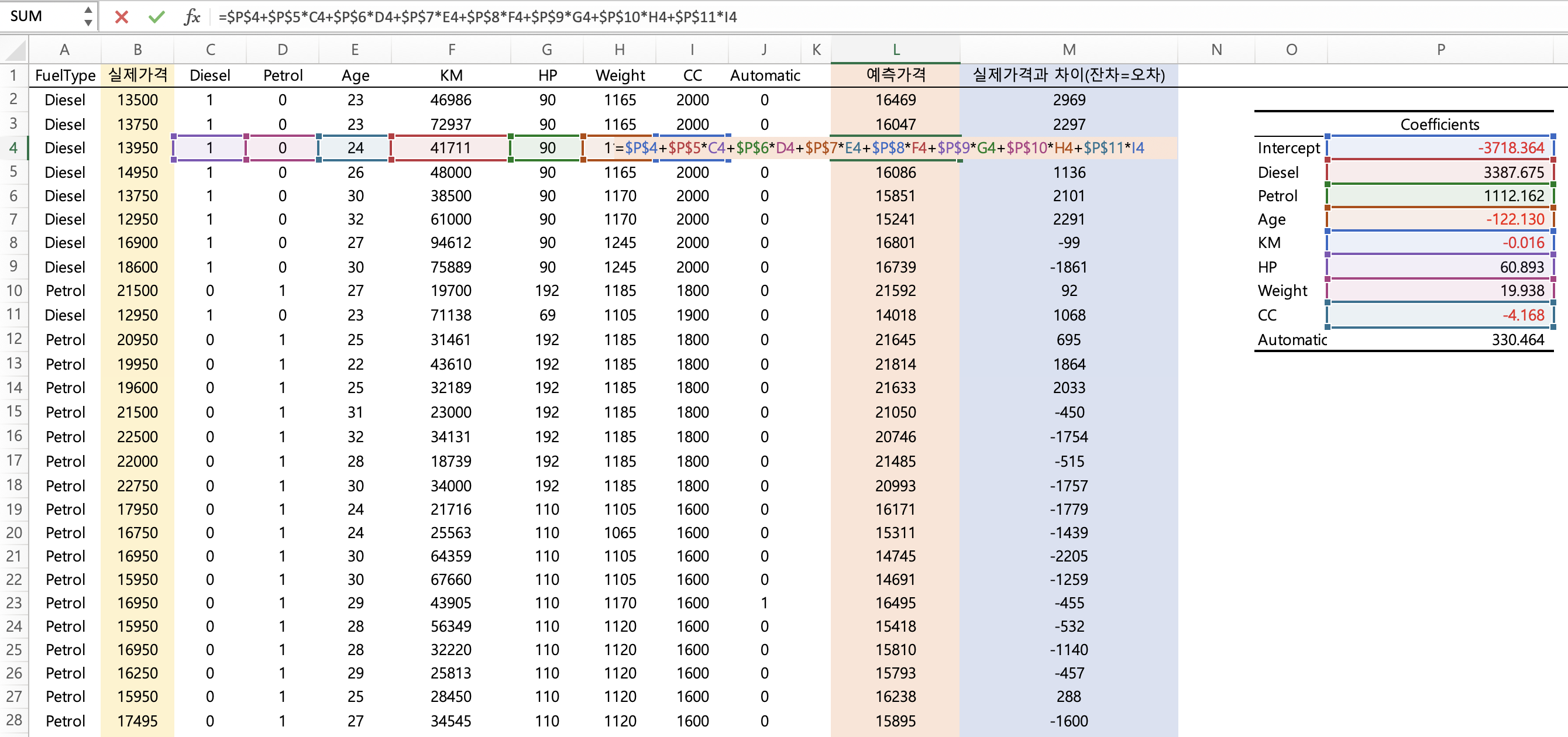
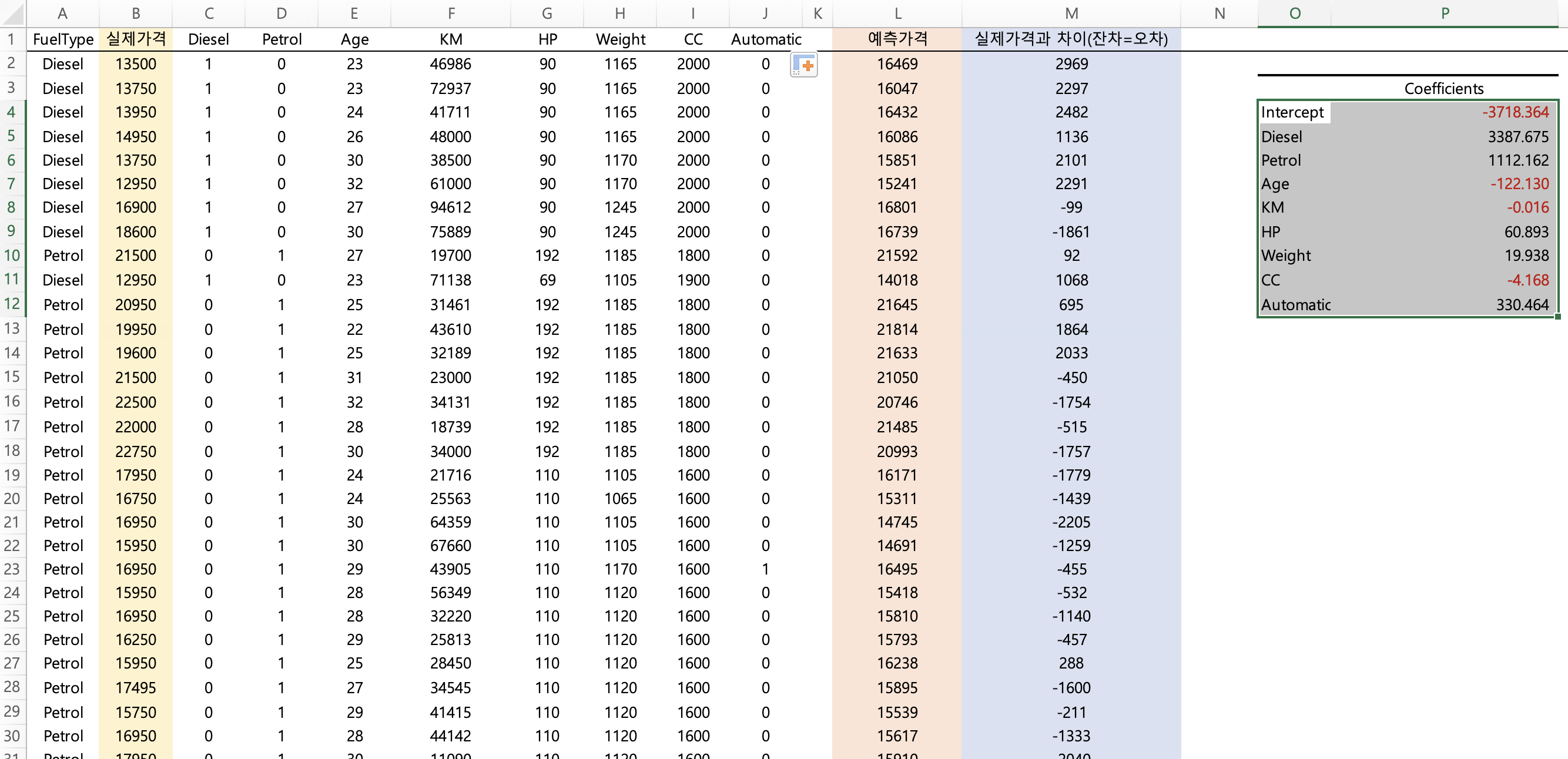
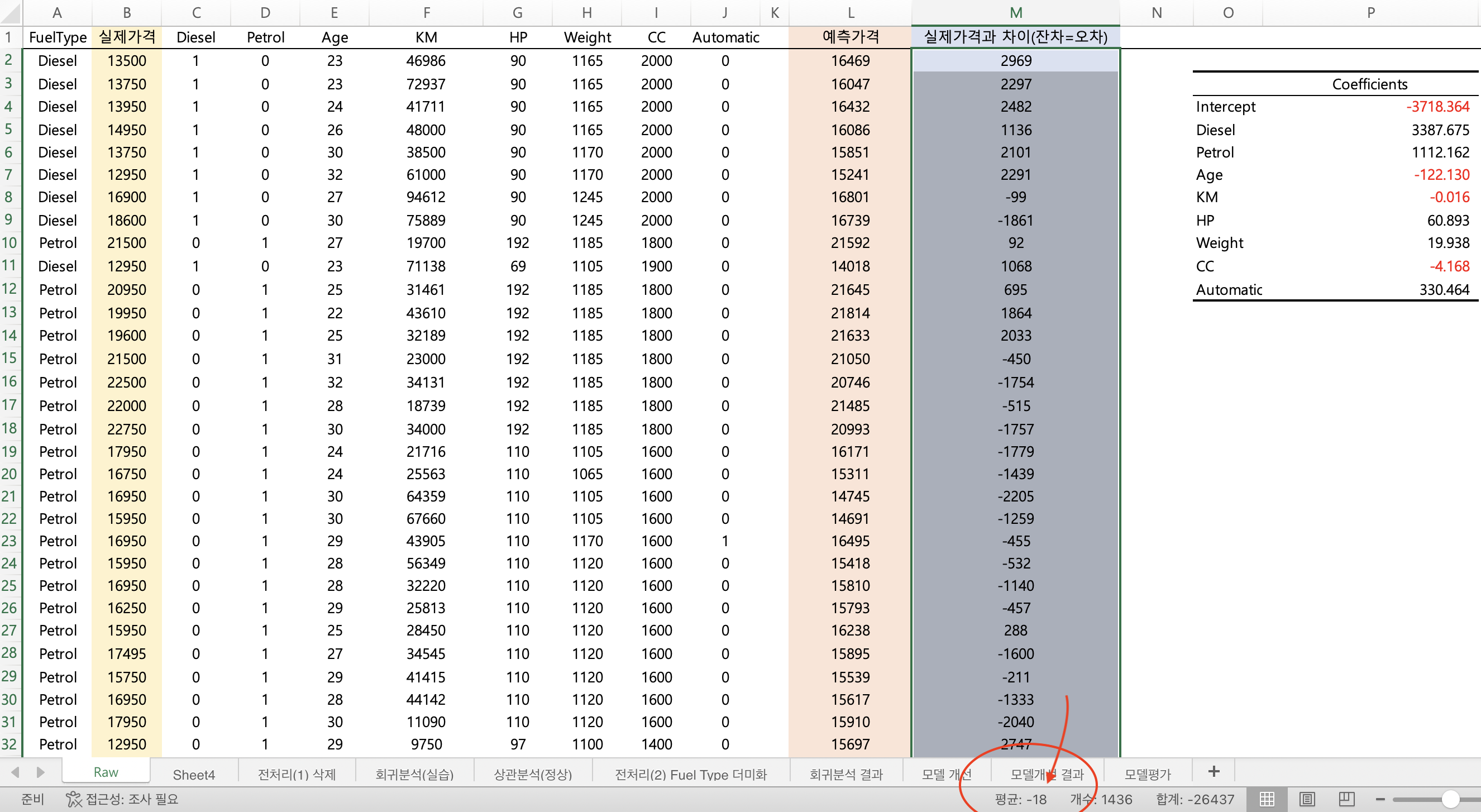
잔차의 평균은 -18입니다.

회귀분석 평가(MAE, RMSE)

MAE 구하기

• 잔차 구하기 : 예측가격 - 실제가격
• 잔차 절대값 : =abs(잔차값)
  참고로 abs는 양수든 음수든 절대값을 구하는 함수입니다.
• 잔차 절대값 총 합 =sum() / 잔차 절대값 총 갯수=count()가 MAE 입니다.

RMSE 구하기

• 잔차 구하기 : 예측가격 - 실제가격

• 잔차 제곱근 : =power(잔차값, 2) 라면 잔차값의 2제곱근

• 잔차 제곱근 총 합 =sum() / 잔차 절대값 총 갯수=count() 로 평균을 구해줍니다.

• 다시 루트 씌워서 원래 값(제곱근) 구하기 : =sqrt()

MAE는 954, RMSE 1313 이 나왔습니다.

변수들을 제거/추가 등을 해주면서 최선의 MAE, RMSE 값을 찾아 나가면 됩니다.

회귀분석은 이렇게 계속해서 오차의 값을 줄여나가서 최선의 값을 구하는 겁니다.