방통대 출석과제 30점만점 받은 기념으로 작성합니다.

변수Murder, Assault, Rape는 인구 100,000명당 사고건수이고
UrbanPop은 도시인구 비율을 나타낸다.

R

방식1

파일 불러오기

문자열 변수 제외

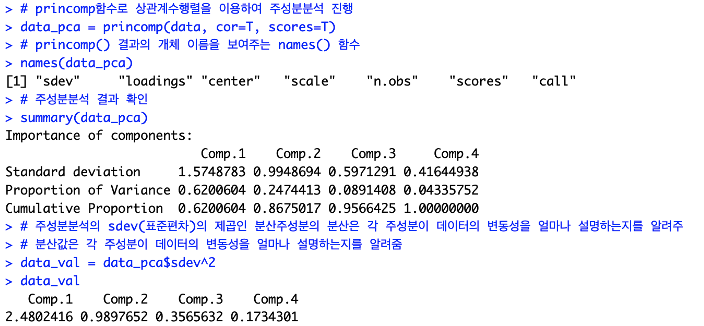
주성분분석

스크리그림

> # 스크리그림 Scree Plot = 주성분의 고윳값 크기 순으로 그림
> screeplot(data_pca, type = "lines" , pch = 19, main = "Scree Plot") 

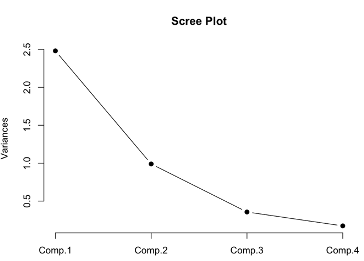
누적분산그림

> # 누적분산 그림 그리기 = 주성분의 표준편차를 제곱하여 분산을 구한 후 plot gkatn dldyd
> data_var = data_pca$sdev^2
> data_var 

> data_var_ratio = data_var / sum (data_var) 
> round(data_var_ratio, 3) 

> plot(cumsum(data_var_ratio), type = 'b', pch=19, xlab = 'Component', ylab = 'Cumulative Proportion') 

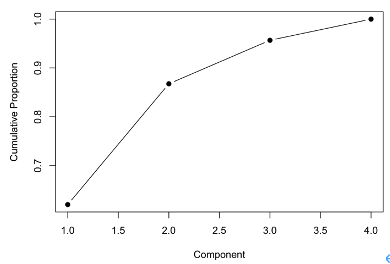
주성분계수

2열만 진행합니다.

행렬도

각 개체에 대한 1~2번째, 그리고 1~3번째 주성분점수 및 행렬도를 확인합니다.

1~2번째

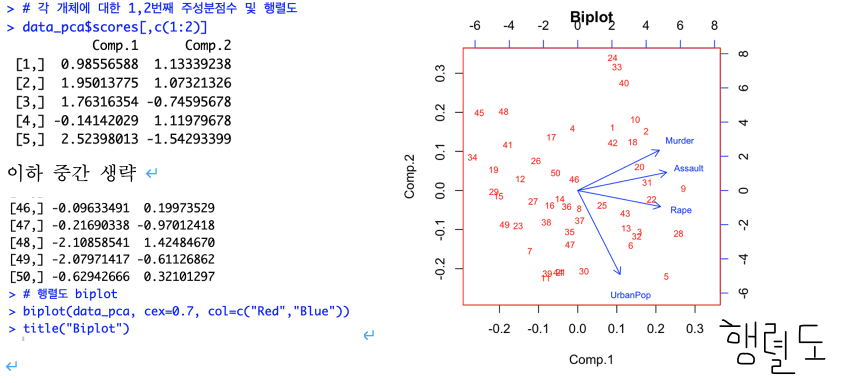
행렬도(Biplot)을 보면 가까운 거리와 비슷한 방향일수록 변수들의 상관성은 높아집니다.
Murder, Assault, Rape은 서로 가까운 곳에 위치하고, UrbanPop은 다른 변수들과 다소 다른 방향에 위치하고 있습니다. 그러므로 UrbanPop은 다른 세 변수들과의 상관성은 낮은 것으로 보여집니다.

1~3번째

스크리그림과 누적분산그림을 보면 Comp.2값이 아닌 Comp.3 값까지 유효한 것으로 보여집니다. 각 개체에 대한 1~3번째 주성분점수 및 행렬도를 다시 해보겠습니다.

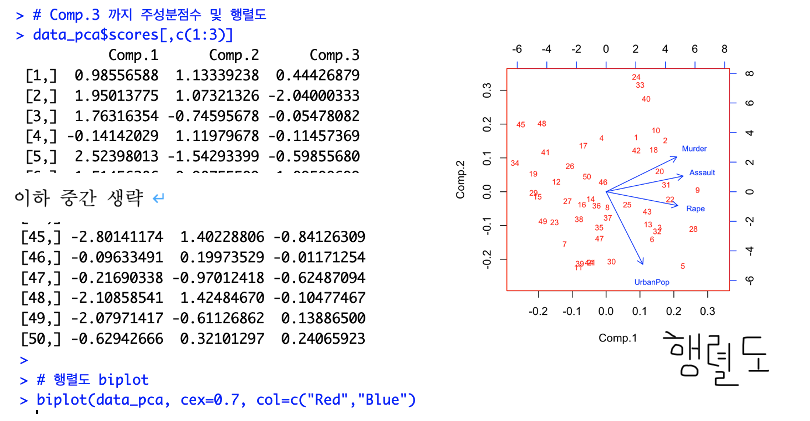
주성분분석 개체가 2개여도 3개여도 행렬도에는 크게 상관 없는 것으로 보여집니다.

방식2

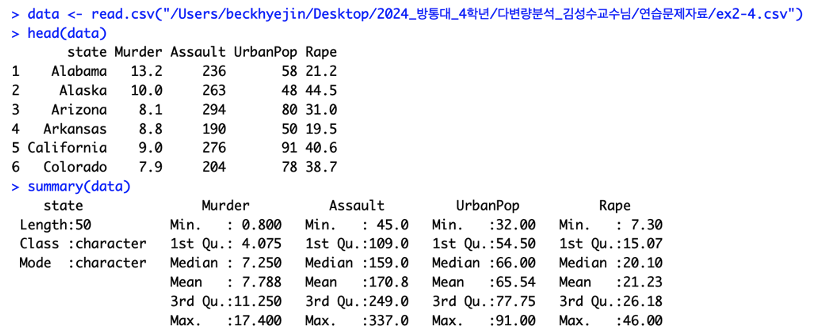
파일 불러오기

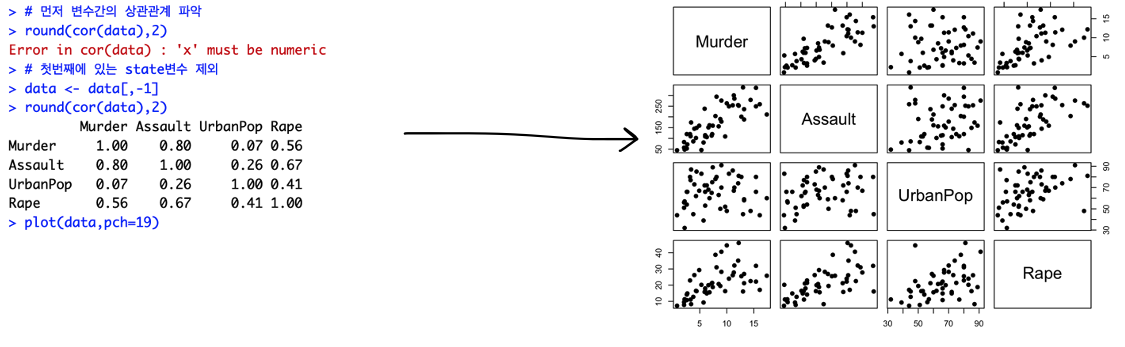
상관관계(산점도행렬)

주성분분석

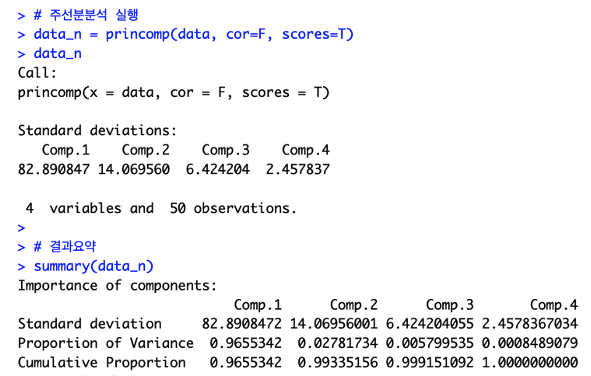
스크리그림

> # 스크리 그림
> screeplot(data_n, type='lines', pch = 19)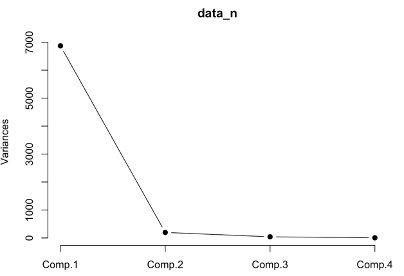 

행렬도 (2개)

스크리그림에서 유효한 주성분을 2개로 판단하여, 처음 2개의 주성분의 계수로 진행해보겠습니다.

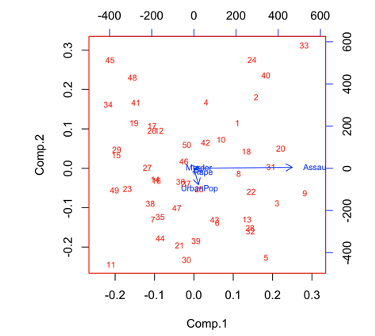
방식1과는 다른 결과(행렬도)가 나와서 놀랍습니다!
이번에는 Assaul가 다른 변수들과 연관성이 낮은 것으로 보여집니다.

참고로 아래가 방식1의 행렬도였습니다.

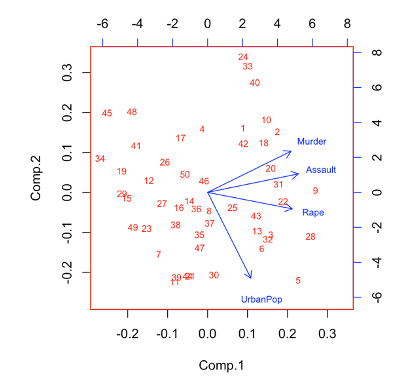
Python

파일 불러오기

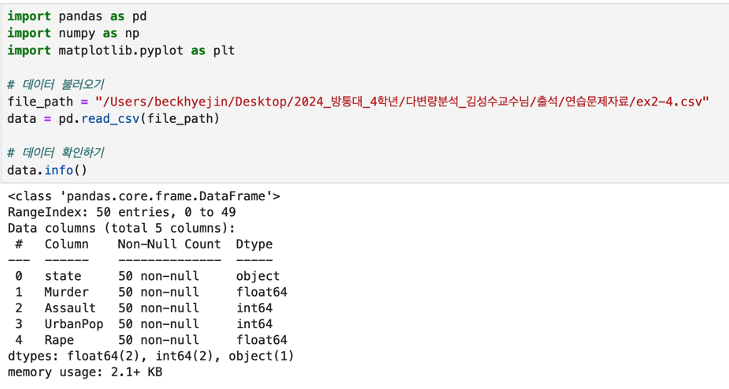
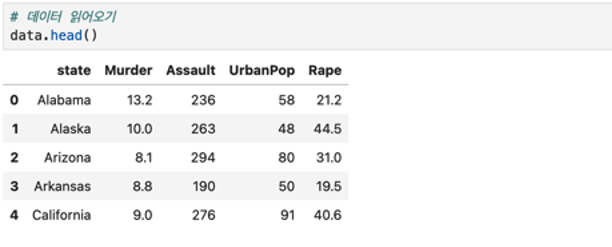
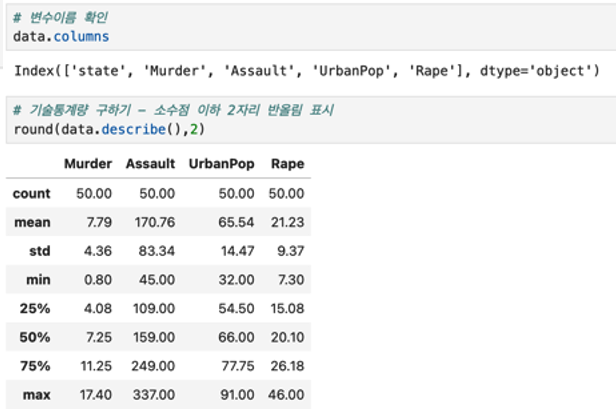
표준화

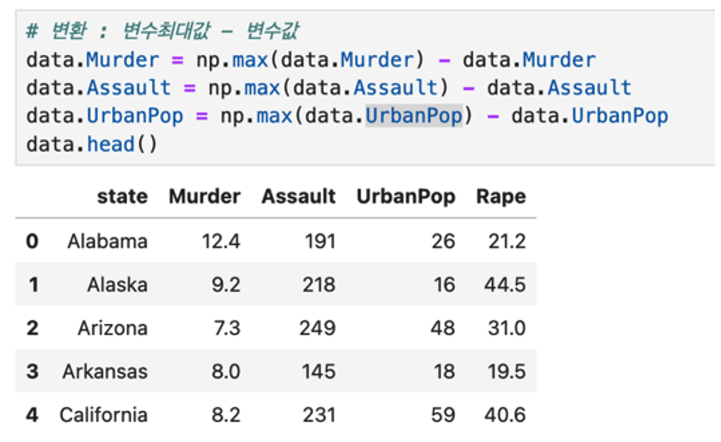
초기 주성분분석

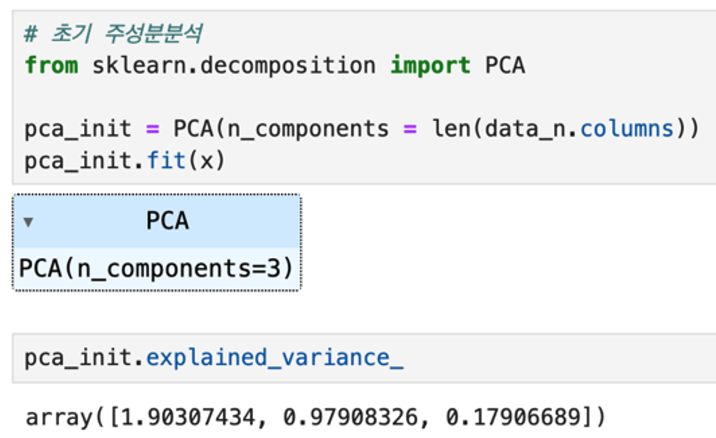
스크리그림

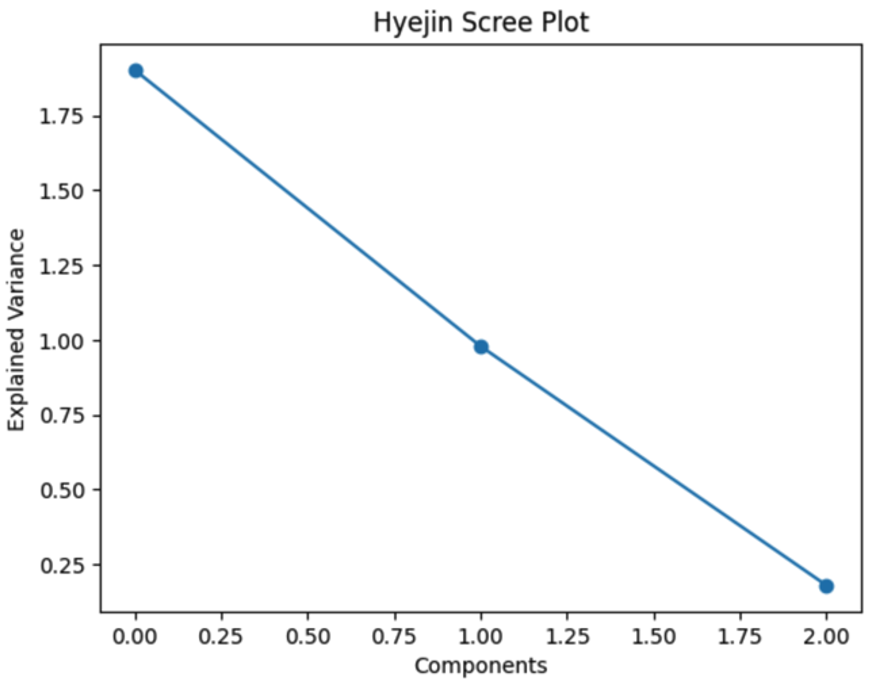
주성분분석 (2개)

주성분의 수를 2개로 하여 주성분을 재실행해보겠습니다.