방통대 과제 30점(만점) 맞은 기념으로 올리는 글입니다.

자동차의 무게가 무거우면 이를 움직이는 데 더 많은 연료가 소모된다는 것은 알려진 사실이다. 자동차의 무게와 자동차를 1km움직이는 데 필요한 에너지의 양과의 함수관계를 정확히 판단하기 위하여 A자동차회사는 다음의 자료를 실험을 통하여 얻었다. 실험비용이 많이 드는 관계로 9번만 실험하였다.

산점도와 회귀직선

설명변수x는 ‘자동차의 무게’ (단위 1,000kg) 이고, 반응변수y는 에너지 소모량 (1,000Btu) 입니다.

x에 대한 y의 산점도를 그리고, 회귀직선을 산점도 위에 그려 넣으시오.

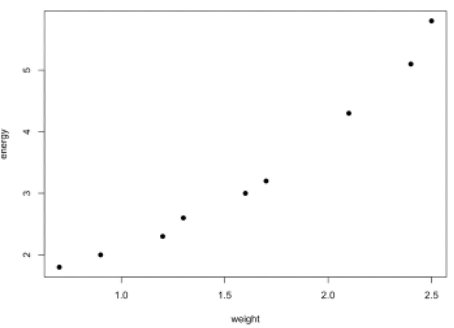
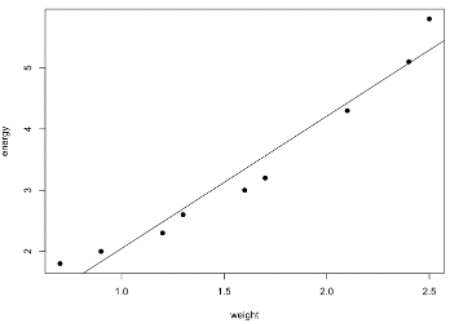
자동차 무게(x)와 에너지 소모량(y)의 산점도와 그 위에 그려놓은 회귀직선 입니다.
자동차 무게가 증가하면, 에너지 소모량도 증가한다는 사실을 알 수 있습니다.
그 관계는 대략 직선이라는 것도 알 수 있다.

ANOVA 분산분석표

회귀직선의 유의여부를 검정하기위해 분산분석표를 작성해보겠습니다.

유의수준a = 0.05 입니다.

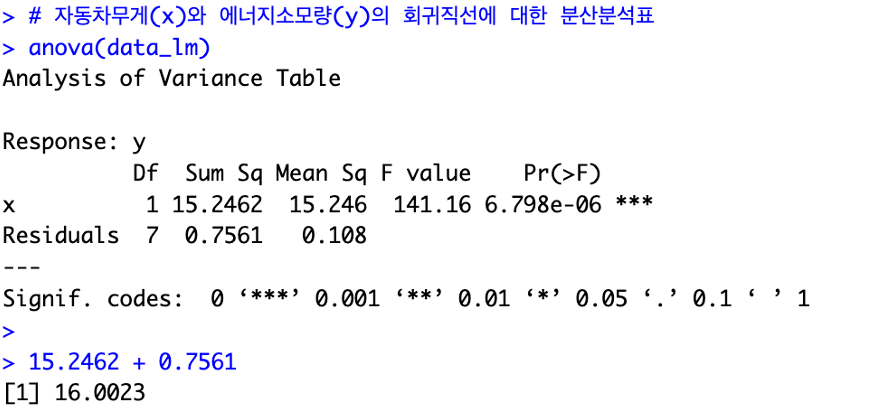
Anova결과를 이용하여 분산분석표 양식으로 정리하면 다음과 같습니다.

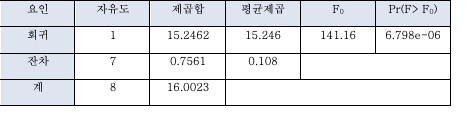
여기서 유의수준 a = 0.05수준에서 F – 기각역 F(1,7;0.05)의 값은

으로, “F0 = 141.16 > F(1,7;0.05) = 5.6” 이므로 귀무가설 H0 : B1 = 0 을 기각하여 구해진 회귀직선이 유의하다는 것을 알 수 있습니다.

여기서 유의확률 p값은 Pr(F> F0) = 1 – Pr(F<= F0) = 1 – Pr(F<=141.16) 이므로,

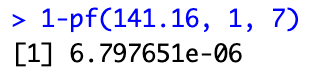
유의확률 값을 이용한 검정은 이 값이 주어진 유의수준 a보다 작으면 귀무가설을 기각합니다. 분산분석표 결과 유의확률 p값은 6.79 x 10-6 으로 아주 작은 값이므로 H0 : B1 = 0 을 기각하게 됩니다.

무게3000kg일때, 에너지소모량 추정

무게 3,000kg이 되는 차량의 에너지 소모량은 어느 정도일지 추정해보겠습니다.

여기에서 회귀방정식은 y = 절편 + 기울기x 로 구하며, y = B0 + B1 x 일 때, y – B0 = B1 x 와 같다. 또한 ( y – B0 ) / B1= x와도 같습니다.
따라서 x = ( y – B0 ) / B1 식을 이용하여 x를 구합니다.
이제 B0 에는 – 0.1157, B1에는 2.1626을, y에는 3000을 대입하여 x인 차량 에너지 소모량 추정치를 구하겠습니다.

무게 3,000kg이 되는 차량의 에너지 소모량의 추정치는 약 1387 (Btb) 입니다.