바이너리 인덱스 트리 (Binary Indexed Tree)

개념

• 2진법 인덱스 구조를 활용해 구간 합 문제를 효과적으로 해결해 줄 수 있는 자료구조
• 펜윅 트리(Fenwick tree)라고도 함

2진수 표기

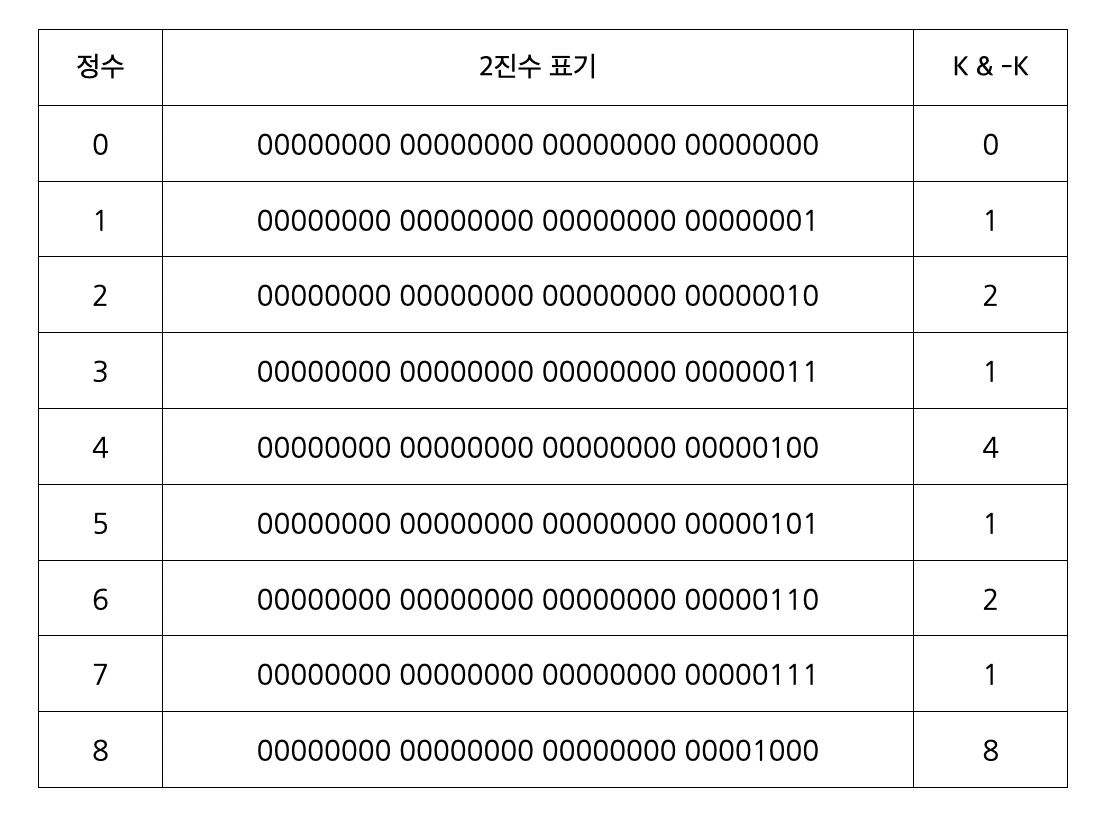
• 특정한 숫자 K의 0이 아닌 마지막 비트를 찾는 방법
  • K & -K 계산

K & -K 계산 결과

트리 구조

• 0이 아닌 마지막 비트 = 내가 저장하고 있는 값들의 개수
  • ex. 1 = 1개, 2 = 2개, 3 = 1개, 4 = 4개
    

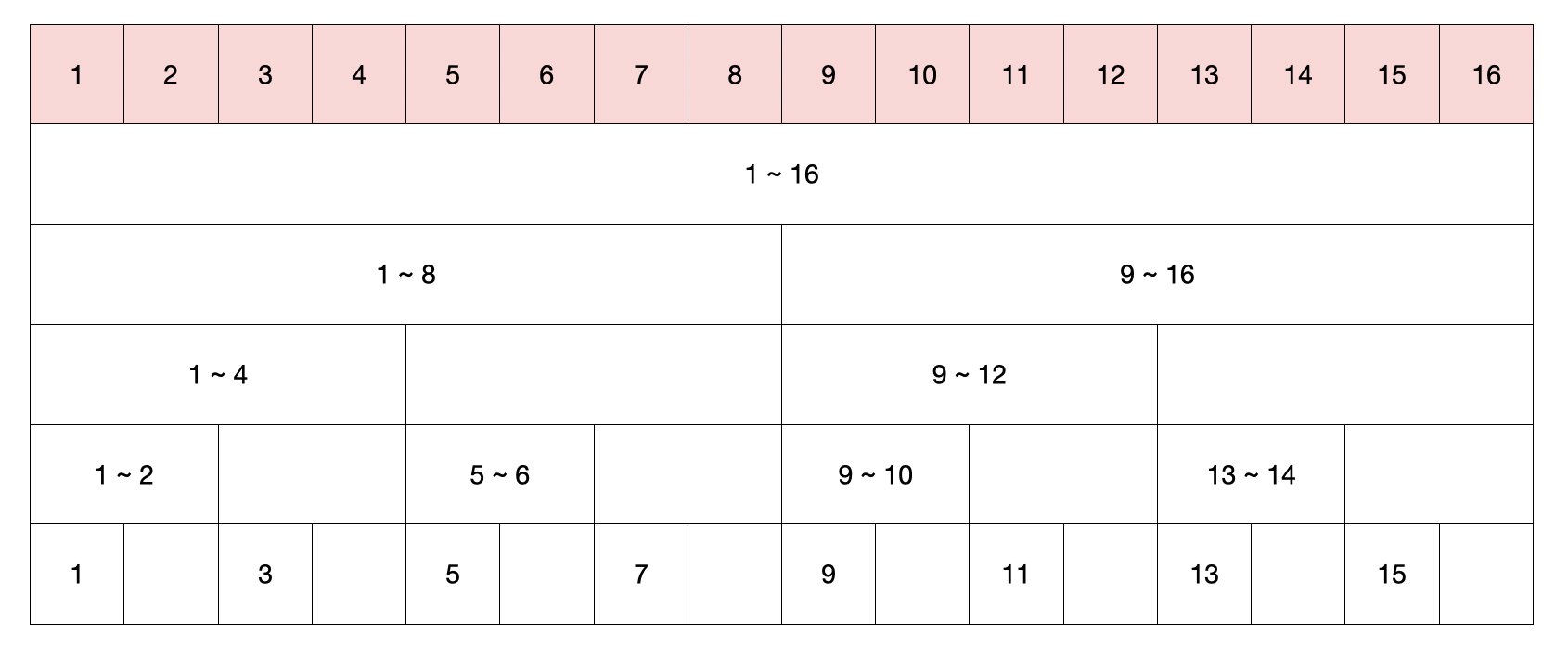
• 특정 값을 변경할 때
  • 0이 아닌 마지막 비트만큼 더하면서 구간 값 변경
• 1부터 N까지 합(누적 합) 구하기
  • 0이 아닌 마지막 비트만큼 빼면서 구간들의 합 계산

소스 코드 (Python)

import sys
input = sys.stdin.readline

# 데이터의 개수(n), 변경 횟수(m), 구간 합 계산 횟수(k)
n, m, k = map(int, input().split())

# 전체 데이터의 개수는 최대 1,000,000개
arr = [0] * (n + 1)
tree = [0] * (n + 1)

# i번째 수까지의 누적 합을 계산하는 함수
def prefix_sum(i):
    result = 0
    while i > 0:
        result += tree[i]
        # 0이 아닌 마지막 비트만큼 빼가면서 이동
        i -= (i & -i)
    return result

# i번째 수를 dif만큼 더하는 함수
def update(i, dif):
    while i <= n:
        tree[i] += dif
        i += (i & -i)

# start부터 end까지의 구간 합을 계산하는 함수
def interval_sum(start, end):
    return prefix_sum(end) - prefix_sum(start - 1)

for i in range(1, n + 1):
    x = int(input())
    arr[i] = x
    update(i, x)

for i in range(m + k):
    a, b, c = map(int, input().split())
    # 업데이트(update) 연산인 경우
    if a == 1:
        update(b, c - arr[b]) # 바뀐 크기(dif)만큼 적용
        arr[b] = c
    # 구간 합(interval sum) 연산인 경우
    else:
        print(interval_sum(b, c))

시간 복잡도

• $O(logN)$