Backpropagation

Backpropagation

• 모델을 학습시키려면 Gradient를 알아야 한다.

1. 수치 미분
   • 근사한 도함수를 이용하기 때문에 오차가 누적될 수 있다.
   • Weight와 Data 변수 개수만큼 계산해야 하기 때문에 비효율적이다.
2. 수식을 직접 미분한다.
   • 근사하지 않으므로 오차가 없다.
   • 함수 값 한 번만 계산하면 된다.
   • 하지만 수식에 따라 미분이 어렵다는 단점이 있다.
     • Computational graph를 이용해 Divide & Conquer를 수행하면 된다.

Computational Graph

• 계산 과정을 Node와 Edge로 구성된 그래프 자료구조로 나타낸 것
• 국소적 계산을 전파함으로써 최종 결과를 얻는다.
• 중간 계산 결과를 보관할 수 있다.
• 역전파, 연쇄법칙을 통해 효율적인 미분 계산이 가능하다.

Backpropagation 계산 절차

• Input 신호 $E$에 국소적 미분을 곱하여 전달한다.

1. 덧셈 노드의 역전파
   $z=x+y$
   • $\frac{\partial z}{\partial x}=1, \frac{\partial z}{\partial y}=1$
   • $\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}\times\frac{\partial z}{\partial x}=\frac{\partial L}{\partial z}=1$
   • $\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z}\times\frac{\partial z}{\partial y}=\frac{\partial L}{\partial y}=1$
   • Gradient Distributor: Gradient 분배
2. 곱셈 노드의 역전파
   $z=xy$
   • $\frac{\partial z}{\partial x}=y, \frac{\partial z}{\partial y}=x$
   • $\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}\times\frac{\partial z}{\partial x}=\frac{\partial L}{\partial z}\times y$
   • $\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z}\times\frac{\partial z}{\partial y}=\frac{\partial L}{\partial y}\times x$
   • Swap multiplier: 교차해서 곱한다.

Multi-layer Perceptron에서의 Backpropagation

One Node per Layer

• Notation
  • $w^{(l)}$: l번째 층의 weight scalar
  • $b^{(l)}$: l번째 층의 bias scalar
  • $a^{(l)}$: l번째 층의 activation scalar
• Assumption
  • 은닉층 및 출력층에 Sigmoid 활성함수 사용
  • 정답 $\mathbf{y}$는 0 또는 1인 Binary Classification
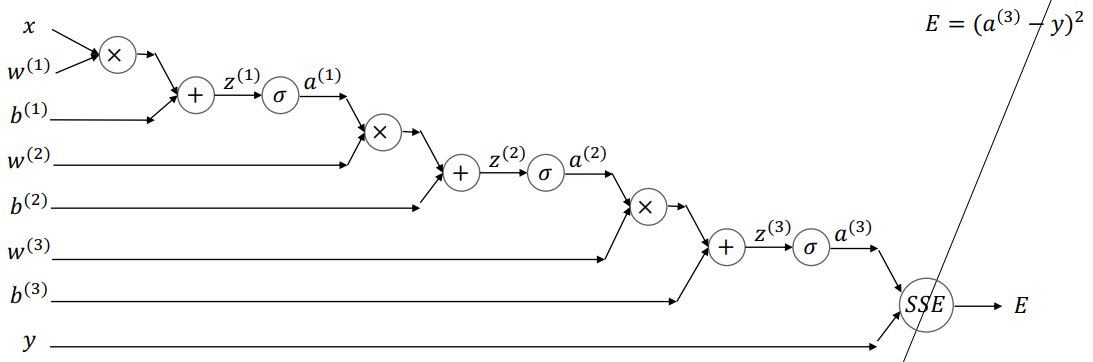
  • 오차함수: SSE

1. Forward

• $x \rightarrow a^{(1)}=S(w^{(1)}x^{(1)}+b^{(1)})\rightarrow a^{(2)}=S(w^{(2)}x^{(2)}+b^{(2)})\rightarrow a^{(3)}=(w^{(3)}x^{(3)}+b^{(3)})$
  

2. Backward

   • $y$는 label이므로 학습 대상이 아니다.

   • Chain Rule에 의해 오차 값이 모든 node에 전달되어 오차에 비례하여 모든 가중치가 갱신된다.

     • $w^{(1)}$의 변화가 $E$에 직접 영향 주는 것은 아니지만 일정 비율 영향을 미친다.
     • $\frac{\partial E}{\partial w^{(1)}}$: $w^{(1)}$이 바뀔 때 $E$가 변화하는 비율
     • $w^{(1)}$의 변화 $\rightarrow z^{(1)}$의 변화 $\rightarrow a^{(1)}$의 변화 $\rightarrow w^{(2)}$의 변화 $\rightarrow z^{(2)}$의 변화 $\rightarrow a^{(2)}$의 변화 $\rightarrow w^{(3)}$의 변화 $\rightarrow z^{(3)}$의 변화 $\rightarrow a^{(3)}$의 변화 $\rightarrow E$의 변화
       

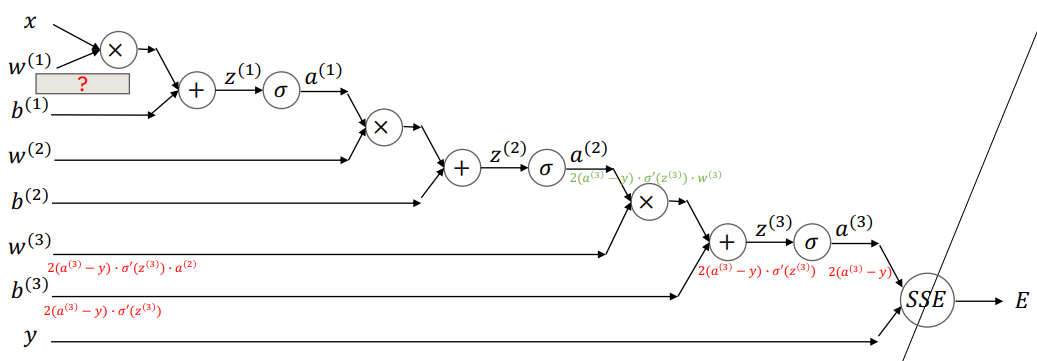
   • Cahin Rule을 적용하면 layer 개수가 아무리 많아도 모든 층에서 가중치에 대한 편미분 값을 구할 수 있다.

Few Nodes per Layer

• Notation
  • $w_{12}^{(l)}$: 이전층 1번 노드와 다음층 2번 노드를 이어주는 $l$번째 층의 weight scalar
  • $b_1^{(l)}$: $l$번째 층 1번 노드에 대한 편향 값
  • $a_1^{(l)}$: $l$번째 층 1번 노드에 대한 활성 값
• Assumption
  • 은닉층에는 ReLU 활성화함수, 출력층에는 Softmax 함수를 사용한다.
  • 오차함수: 교차 엔트로피

1. Forward

   $Z^{(1)}=XW^{(1)}+B^{(1)}$
   • $Z[1\times m] = X[1\times n]\times W[n \times m]+B[1\times m]$
     • 앞 층 노드 개수 $n$, 뒤 층 노드 개수 $m$
   • $A^{(1)}=\text{ReLU}(Z^{(1)})=\max(Z^{(1)}, 0)$
     

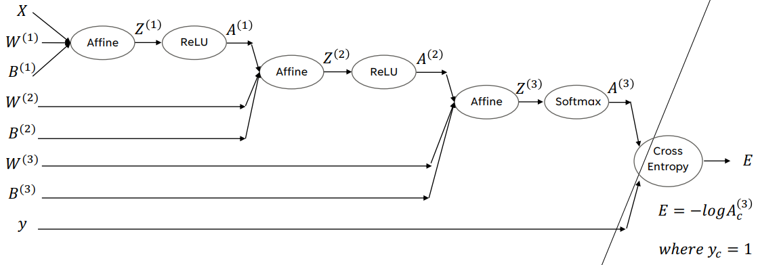
2. Backward

   • 매우 복잡한 과정이다.
     • Pytorch, tensorflow 등의 프레임워크에 backward pass 코드가 이미 구현되어 직접 계산하지 않아도 된다.

Generalized Multi-Layer Perceptron

• 입력층: $28\times28$ 이미지 (784개 노드)
• 2개의 은닉층 (각 층 노드 16개), ReLU
• 출력층: 10개의 노드 (digit), Softmax

1. Forward
   
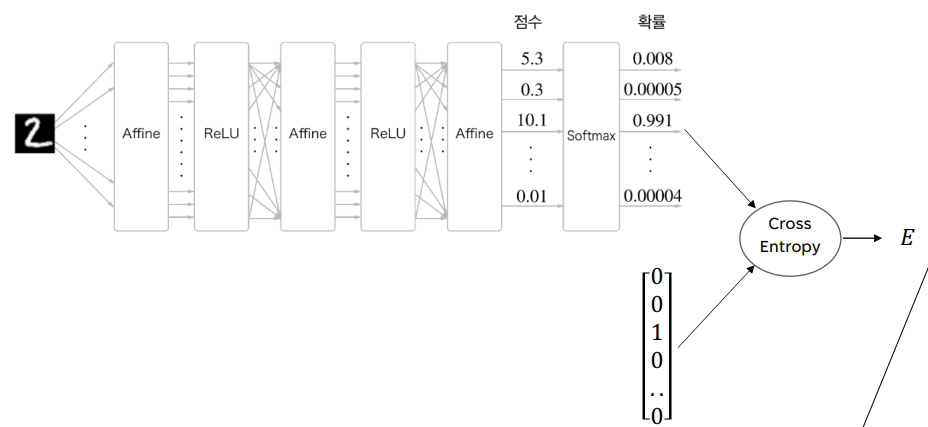
   • 총 가중치 (ReLU는 가중치 없음)
     • Affine 1: $784 \times 16 + 16$
     • Affine 2: $16 \times16 + 16$
     • Affine 3: $16 \times10 + 10$
     • Total: 13002
2. Backward
   • One Node per Layer와 동일한 원리로 진행된다.