Multi-Layer Perceptron Training

Generalized Multi-Layer Perceptron

• 여러 개의 데이터가 동시에 입력으로 들어오는 경우
  
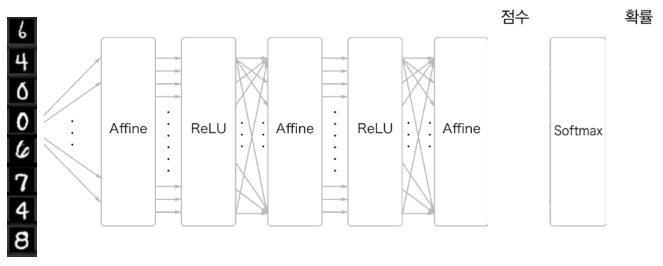
  • 위의 경우 $X$는 $[8\times784]$
  • Batch size가 $N$일 때 $[N\times784]$
  • 기존에 $Z[1×m]=X[1×n]×W[n×m]+B[1\times m]$인 것과 달리
    • $Z[N\times m]=X[N\times n]×W[n\times m]+B[1\times m]$
    • Bias의 경우 broadcasting으로 연산이 진행된다.
  • Mini-Batch 학습
  • Softmax는 각 데이터 별로 개별적으로 수행된다.
    • Corss Entropy의 경우에도 각 데이터 별로 개별적으로 수행된다.
    • 최종 손실함수 $E$는 개별 데이터의 손실함수의 평균으로 계산된다.

Mini-Batch Training

• 고차원 데이터는 전체 데이터셋을 한번에 다 처리하기 어렵기 때문에 Mini-Batch Training이 필요하다.
• Batch Size
  • 배치 크기를 1로 설정할 경우 Gradient가 너무 튀는 문제가 있다.
  • 배치 크기를 최대로 설정하면 Gradient가 뭉개지는 문제가 있다.
  • 적절한 배치 크기를 Hyperparameter로 설정할 필요가 있다.
    • 일반적으로 8, 16, 32, 64 등 2의 거듭제곱 수를 사용한다.
• Epoch: 전체 데이터셋을 한 번씩 학습하는 것
• Iteration: 가중치 업데이트를 한 번 수행하는 것
• Batch size: 한 iteration을 수행하는 데 사용하는 학습 데이터 개수

Training Data Split

• 주어진 데이터를 모두 학습에 사용하면 평가에 사용할 데이터가 없다. 따라서 정확도가 높게 나올 수밖에 없다.
• Training set (70%): 모델을 학습시키는 데 사용
• Validation set (15%): Hyperparameter를 결정하는 데 사용
• Test set (15%): 최종 모델의 성능을 평가하는 데 사용
• MNIST eample
  • 60,000개의 training set과 10,000개의 test set을 포함한다.
  • Batch size가 32일 때 epoch의 총 iteration 수는 60000 ÷ 32 = 1875
  • Batch size가 64일 때 epoch의 총 iteration 수는 60000 ÷ 64 = 937.5 (983)

Optimizer

Limitation of SGD

• 비등방성 함수에 대해 수렴이 느리다.
  • 각 위치에서의 기울기가 가리키는 지점이 하나가 아니라 여러개인 함수
  • 지그재그 방향으로 학습이 수행된다.
• Saddle Point에서 학습이 종료될 수 있다.
  • 어느 축에서 보면 극대값이지만 다른 축에서는 극소값이 되는 지점
  • 고차원 공간에 많이 존재한다.

SGD + Momentum

• 현재 step의 gradient가 아닌 속도 방향으로 가중치를 업데이트한다.

• 이후 속도 방향을 업데이트한다.

  SGD	SGD + Momentum
  $W=W-\rho\frac{\partial E}{\partial W}$	$W=W-\rho V, V=\alpha V+\frac{\partial E}{\partial W}$
  $W$: 가중치	$V$: 속도
  $\rho$: 학습률	$\alpha$: 마찰 계수

• SGD의 단점

  • 학습 경로가 smooth 해지는 효과
  • 관성으로 인해 saddle point 탈출 가능

Adaptive Learning Rate

• 기존 SGD는 모든 가중치에 대해 동일한 학습률을 사용한다.
  • 가중치 $x$의 학습률을 크게, 가중치 $y$의 학습률은 작게 설정하면 SGD의 단점을 극복할 수 있다.
• 현재 시점으로 최근에 update 폭이 컸던 가중치는 작은 학습률을 할당하고 update 폭이 작았던 가중치는 큰 학습률을 할당한다.
  • $W=W-\rho\frac{1}{\sqrt{H}}\odot\frac{\partial E}{\partial W}$
    • 최근 가중치 update 폭에 반비례하게 가중치를 업데이트한다.
  • 누적 Gradient $H=\beta H+(1-\beta)\frac{\partial E}{\partial W}\odot\frac{\partial E}{\partial W}$
    • 가중치별로 Gradient의 제곱(크기)를 업데이트한다.
    • $\beta$: 감쇄 계수
    • $\odot$: 행렬의 원소별 곱
• ADAM(Adaptive Moment Estimation)
  • Momentum + Adaptive Learning RAte
  • 일반적으로 모델을 학습할 때 Adam optimizer를 쓰면 된다.
  • Momentum, adaptive learning rate 적용하여 가중치 업데이트: $W=W-\rho\frac{1}{\sqrt{H}}\odot V$
  • Momentum 업데이트: $V=\beta_1V+\frac{\partial E}{\partial W}$
  • Adaptive learning rate 업데이트: $H=\beta_2H+(1-\beta_2)\partial{\partial E}{\partial W}\odot\frac{\partial E}{\partial W}$