다익스트라 알고리즘
다익스트라 알고리즘은 다이나믹 프로그래밍, 즉 DP를 활용한 대표적인 최단 경로 탐색 알고리즘이다. 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다. 이 알고리즘이 DP 문제인 이유는 '최단 거리는 여러 개의 최단 거리로 이루어져 있기 때문'이다. 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있다.
다익스트라 알고리즘 동작 로직
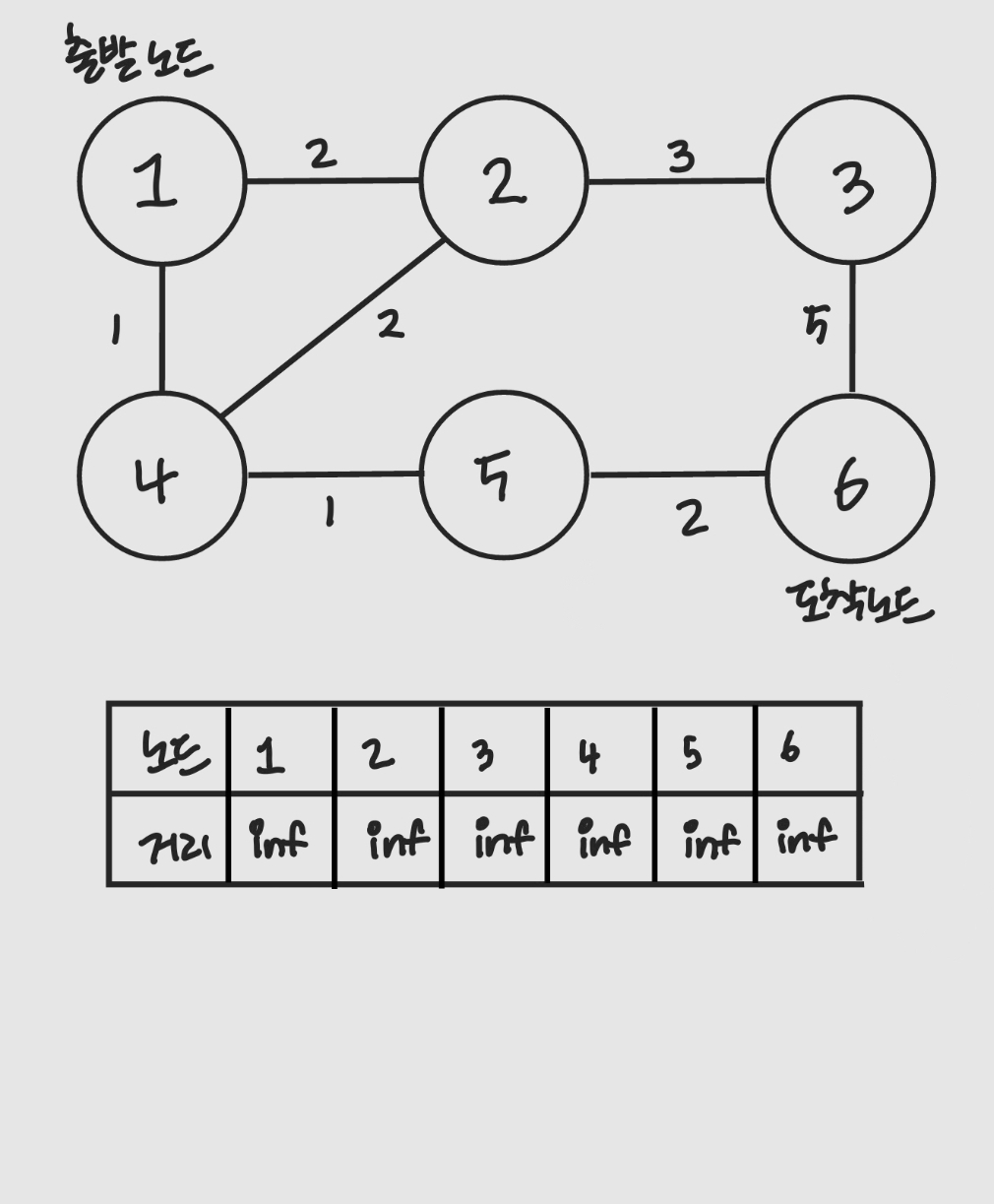
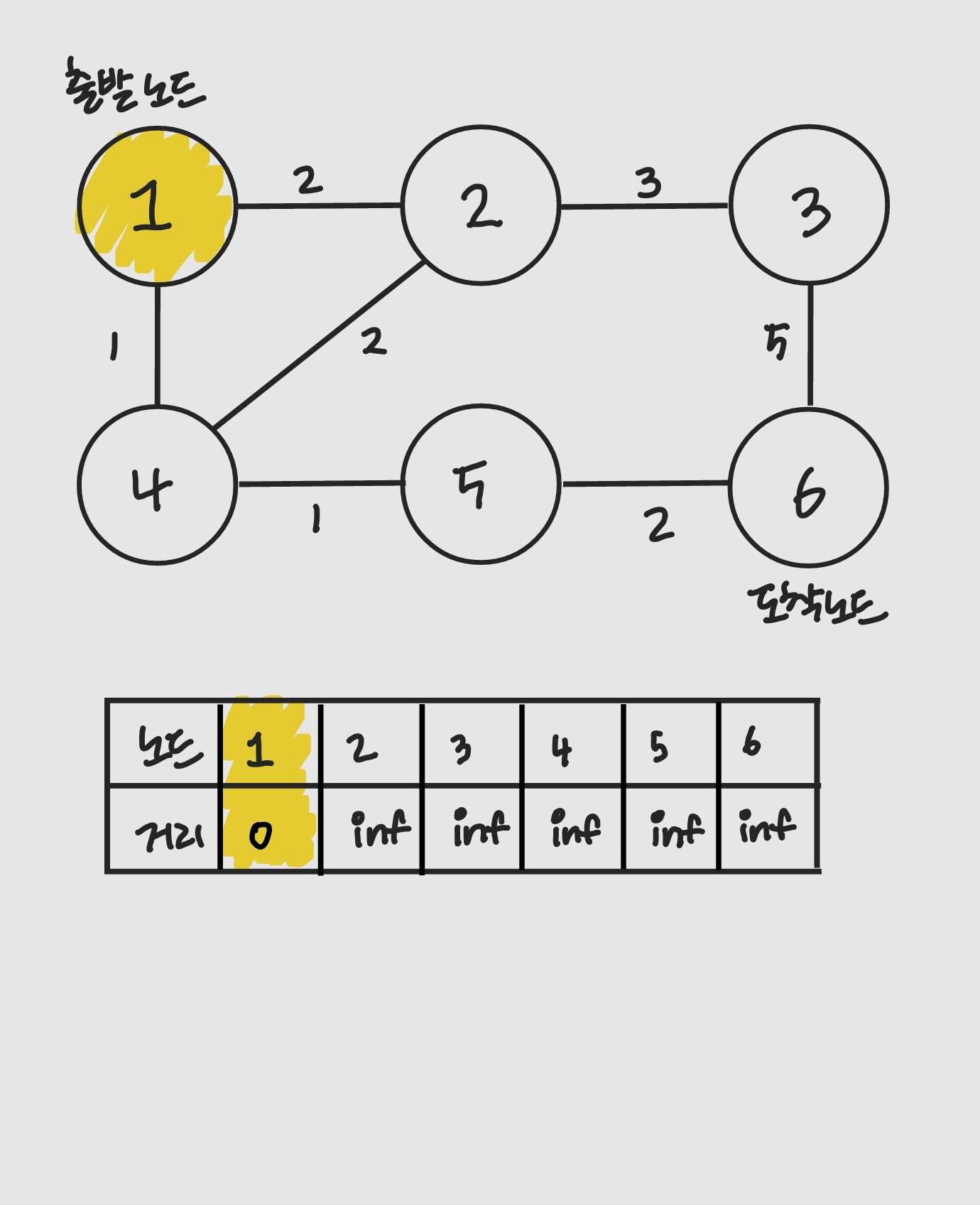
- 출발 노드와 도착 노드를 설정함
- 최단 거리 테이블을 초기화함
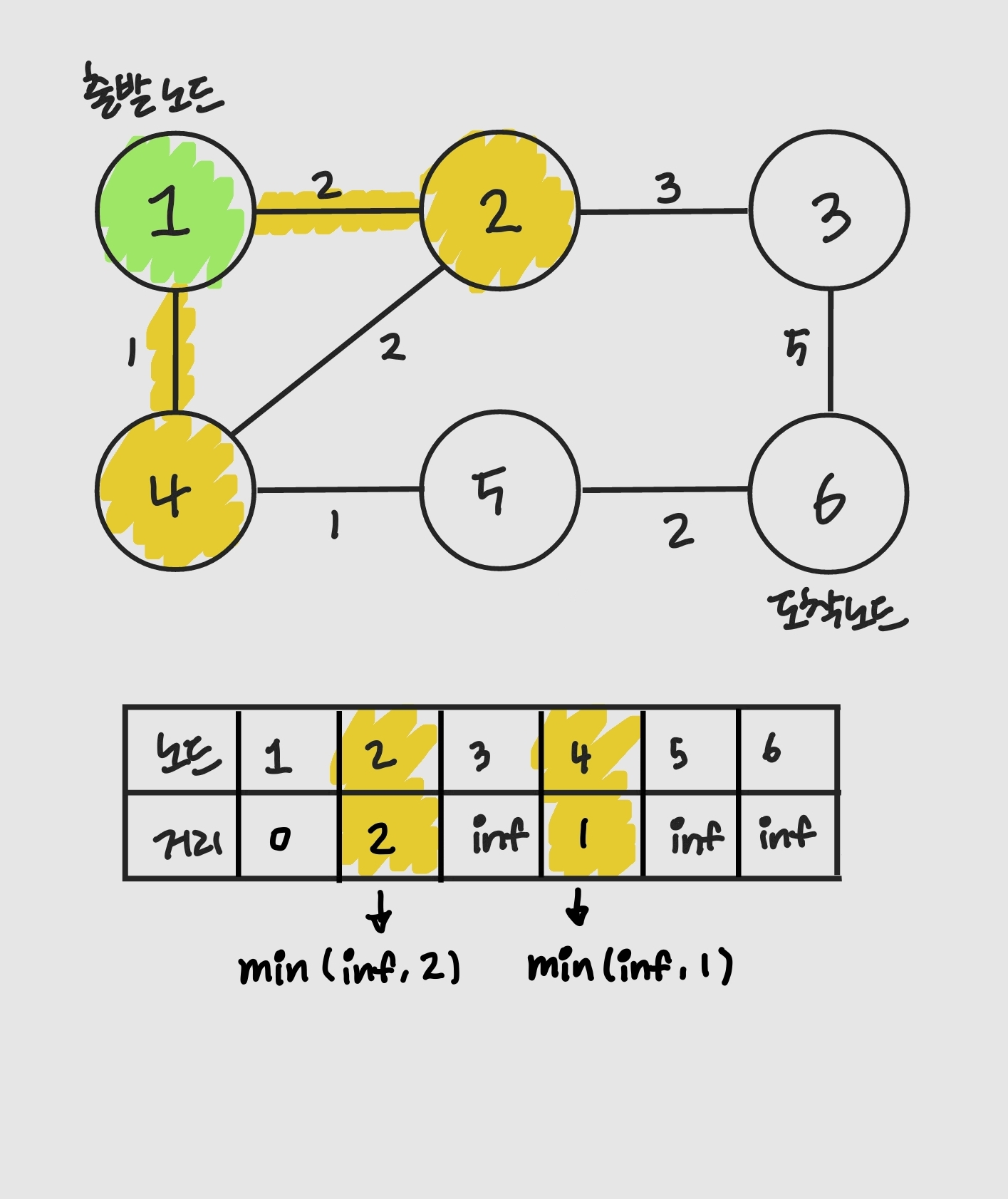
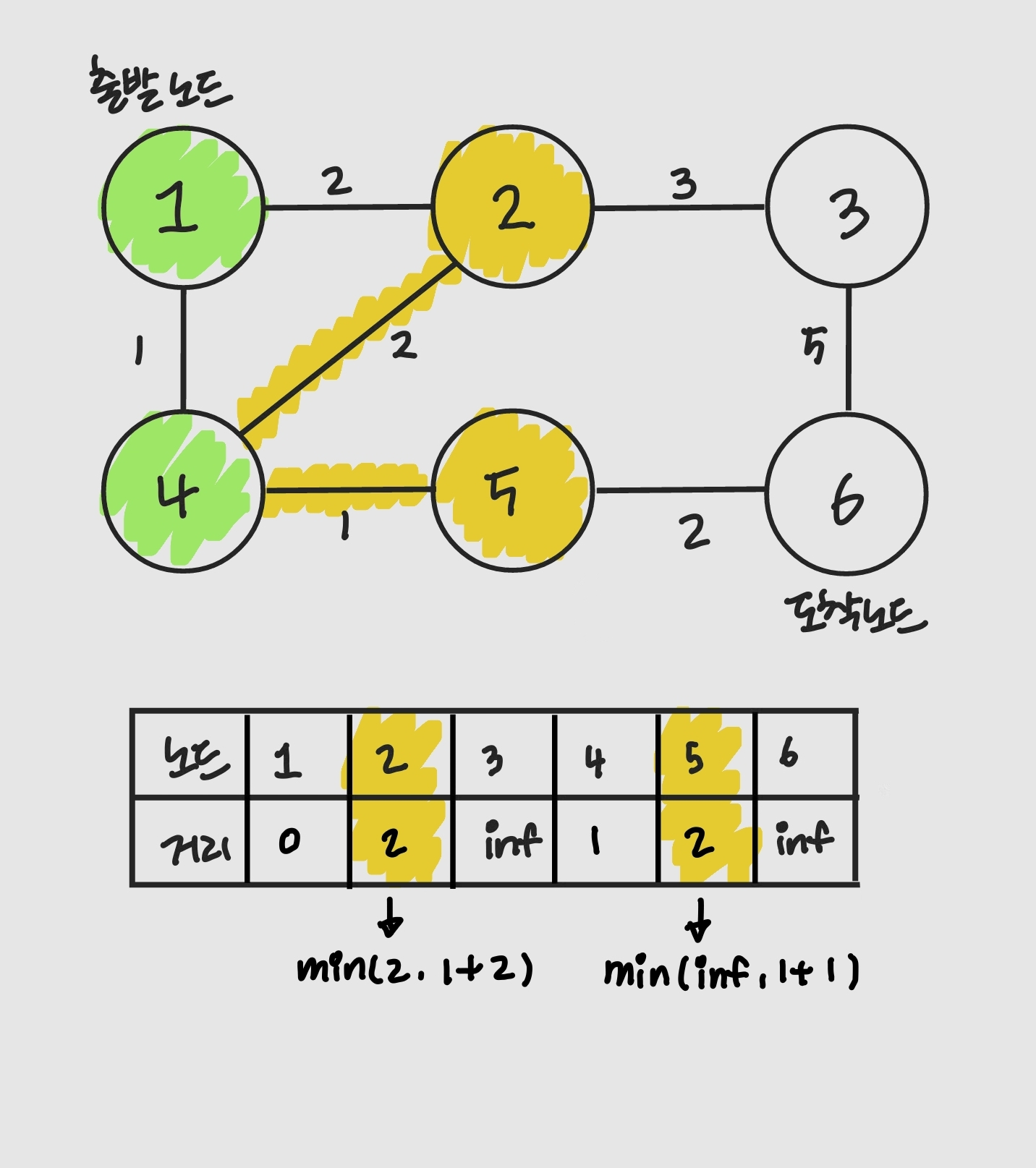
- 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하여 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택함. 그리고 그 노드를 방문 처리함
- 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산하여 최단 거리 테이블을 업데이트함
- 3-4 과정을 반복함
- 최단 거리 테이블에는 N개 노드까지 오는 데 필요한 최단 거리를 기록함
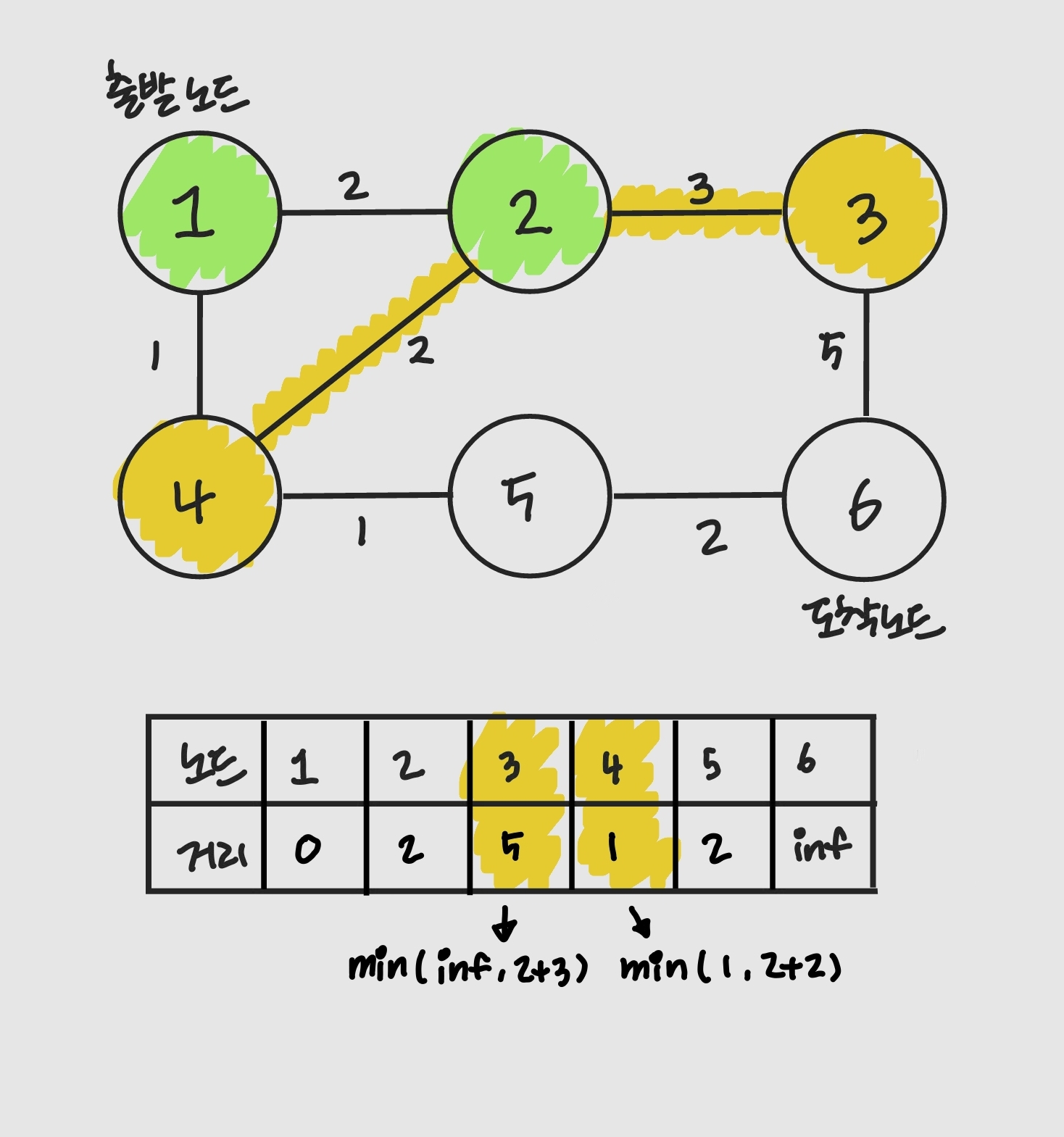
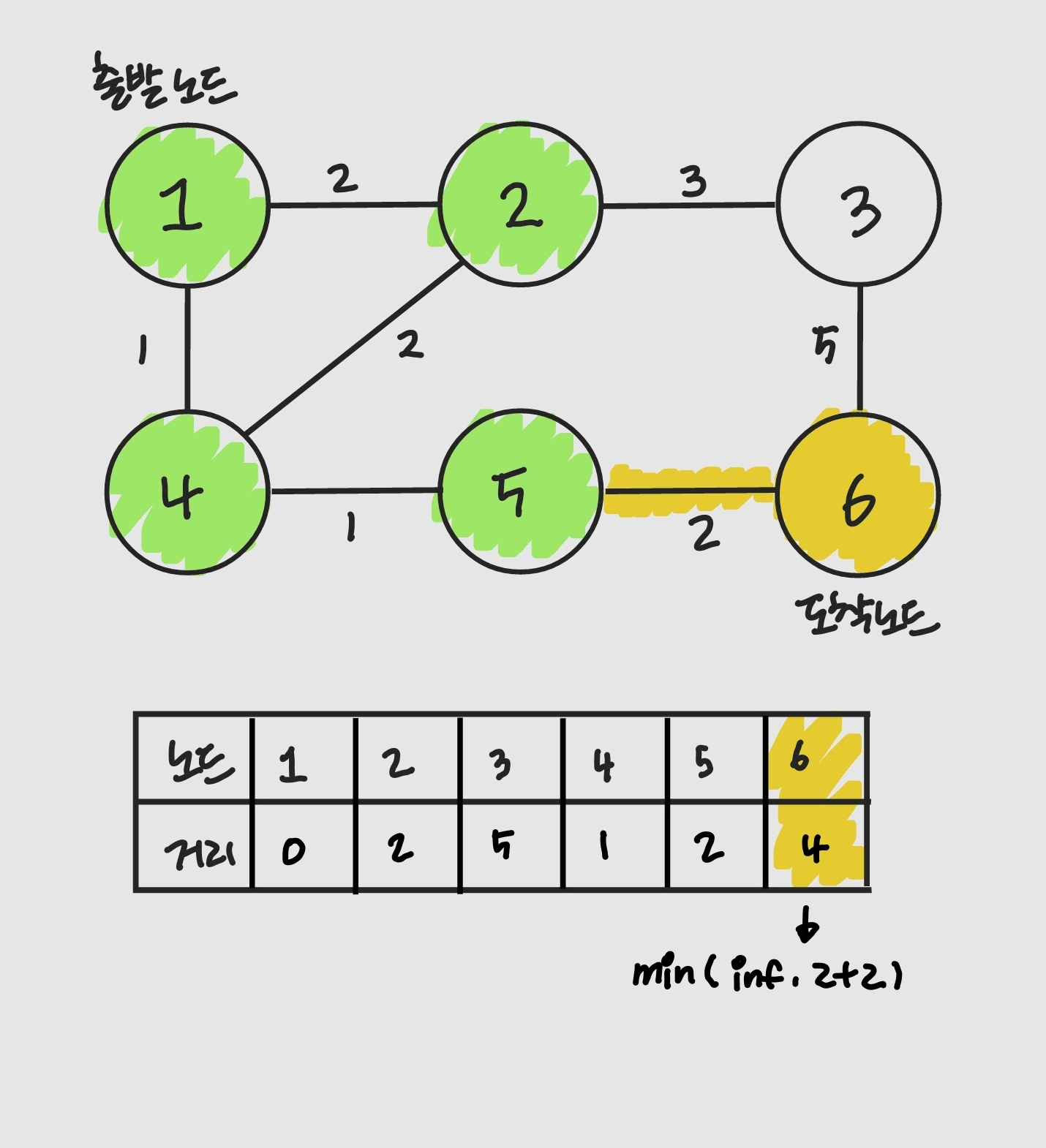
이 다익스트라는 구현시에 방문하지 않은 노드를 다루는 방식에서 순차 탐색을 할 것인지 우선순위 큐를 사용할 것인지로 나뉨.
순차 탐색을 사용한 코드 - 파이썬
이 경우 방문하지 않은 노드 중 거리값이 가장 작은 노드를 선택해 다음 탐색 노드로 삼음. 그 노드를 찾는 방식이 순차 탐색이 됨. 아래에서는 get_smallest_node 함수가 순차 탐색을 수행하는 것을 파악할 수 있다. 따라서 노드 개수가 N개라고 한다면 각 노드마다 최소 거리값을 갖는 노드를 선택해야 하는 순차 탐색이 수행되기에 (N - 1) * N으로 O(N^2)의 시간복잡도를 가진다.
n, m = map(int, input().split())
k = int(input()) # 시작할 노드
INF = 1e8
graph = [[] for _ in range(n+1)] # 1번 노드부터 시작하므로 하나더 추가
visited = [False] * (n+1)
distance = [INF] * (n+1)
for _ in range(m):
u, v, w = map(int, input().split()) # u: 출발노드, v: 도착노드, w: 연결된 간선의 가중치
graph[u].append((v, w)) # 거리 정보와 도착노드를 같이 입력합니다.
def get_smallest_node():
min_val = INF
index = 0
for i in range(1, n+1):
if distance[i] < min_val and not visited[i]:
min_val = distance[i]
index = i
return index
def dijkstra(start):
distance[start] = 0 # 시작 노드는 0으로 초기화
visited[start] = True
for i in graph[start]:
distance[i[0]] = i[1] # 시작 노드와 연결된 노도들의 거리 입력
for _ in range(n-1):
now = get_smallest_node() # 거리가 구해진 노드 중 가장 짧은 거리인 것을 선택
visited[now] = True # 방문 처리
for j in graph[now]:
if distance[now] + j[1] < distance[j[0]]: # 기존에 입력된 값보다 더 작은 거리가 나온다면,
distance[j[0]]= distance[now] + j[1] # 값을 갱신한다.
dijkstra(k)
print(distance)우선순위 큐를 사용한 코드 - 파이썬
순차 탐색을 사용할 경우 노드 개수가 늘어날수록 탐색 시간이 매우 오래 걸릴 수 있다. 따라서 이를 해결하기 위해 우선순위 큐를 도입한다.
거리 값을 담을 우선순위 큐는 힙으로 구현하고 이 우선순위의 기준은 시작 노드로부터 가장 가까운 노드가 된다. 따라서 큐의 정렬은 최단 거리인 노드를 기준으로 최단 거리를 가지는 노드를 앞에 배치한다.
순차 탐색때와는 다르게 이 경우에는 방문 여부를 기록하는 배열은 없어도 괜찮음. 우선순위 큐가 알아서 최단 거리의 노드를 앞으로 정렬하기 때문에 기존 최단 거리보다 크다면 무시하면 그만이기 때문이다. 만약 기존 최단거리보다 더 작은 값을 가지는 노드가 있다면 그 노드와 거리를 우선순위 큐에 넣는다. <거리, 노드>꼴로 넣으면 된다.
이 경우 간선의 수를 E(Edge), 노드의 누를 V(Vertex)라고 할 때 시간 복잡도는 O(ElogV)가 된다. 우선순위 큐에서 꺼낸 노드는 연결된 노드만 탐색하기 떄문에 최악의 경우에도 총 간선 수인 E만큼만 반복한다. 하나의 간선에 대해서는 O(logE)이고, E는 V^2보다 항상 작기 때문에 E개의 간선을 우선순위 큐에 넣었다 빼는 최악의 경우는 O(ElogV)이다.
n, m = map(int, input().split())
k = int(input()) # 시작할 노드
INF = 1e8
graph = [[] for _ in range(n+1)] # 1번 노드부터 시작하므로 하나더 추가
distance = [INF] * (n+1)
for _ in range(m):
u, v, w = map(int, input().split()) # u: 출발노드, v: 도착노드, w: 연결된 간선의 가중치
graph[u].append((v, w)) # 거리 정보와 도착노드를 같이 입력합니다.
import heapq
def dijkstra(start):
q = []
heapq.heappush(q, (0, start)) # 우선순위, 값 형태로 들어간다.
distance[start] = 0
while q:
dist, now = heapq.heappop(q) # 우선순위가 가장 낮은 값(가장 작은 거리)이 나온다.
if distance[now] < dist: # 이미 입력되어있는 값이 현재노드까지의 거리보다 작다면 이미 방문한 노드이다.
continue # 따라서 다음으로 넘어간다.
for i in graph[now]: # 연결된 모든 노드 탐색
if dist+i[1] < distance[i[0]]: # 기존에 입력되어있는 값보다 크다면
distance[i[0]] = dist+i[1] #
heapq.heappush(q, (dist+i[1], i[0]))
dijkstra(k)
print(distance)다익스트라 장단점
- 장점
- 그래프가 큰 경우에도 사용할 수 있음
- 무차별 접근 방식보다 효율적임
- 경로 추적을 위한 알고리즘으로도 쉽게 수정 가능
- 단점
- 음수인 가중치를 가진 간선이 있는 경우에는 사용할 수 없음
- 그래프와 거리를 저장하기 위해서는 많은 양의 메모리가 필요함
- 동일한 거리에 여러 경로가 있는 경우 최상의 경로를 보장하지 않음
참고
https://velog.io/@717lumos/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BCDijkstra-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://velog.io/@tks7205/%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-with-python
