병합 정렬 (Merge Sort)

병합 정렬이란?

분할 정복(Divide & Conquer) 기법을 사용한 알고리즘 중 하나로 재귀를 이용하기도 한다. 주어진 배열을 원소가 하나밖에 남지 않을때까지 계속 둘로 쪼갠 후에 크기순으로 재배열하면서 원래 크기의 배열로 합친다.

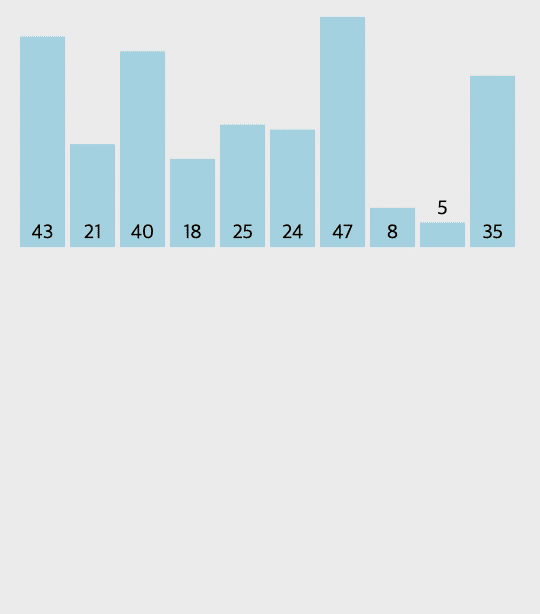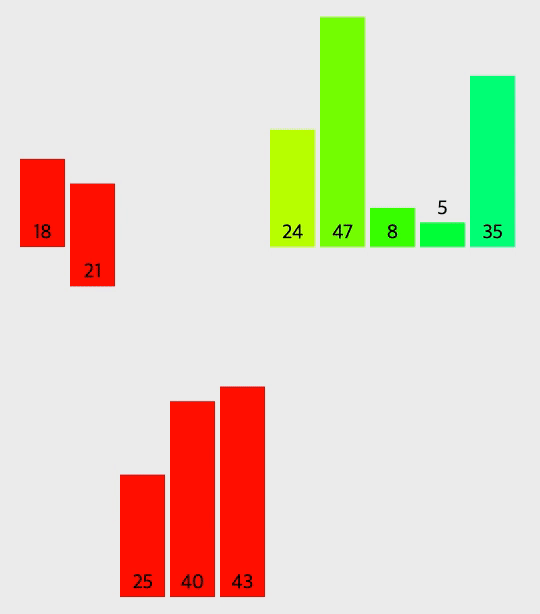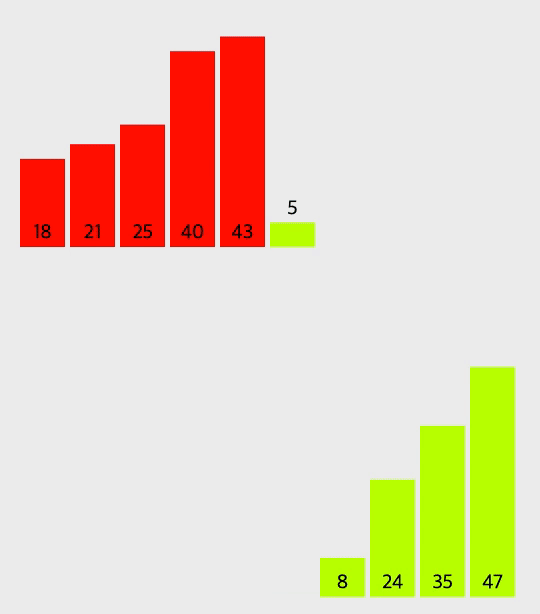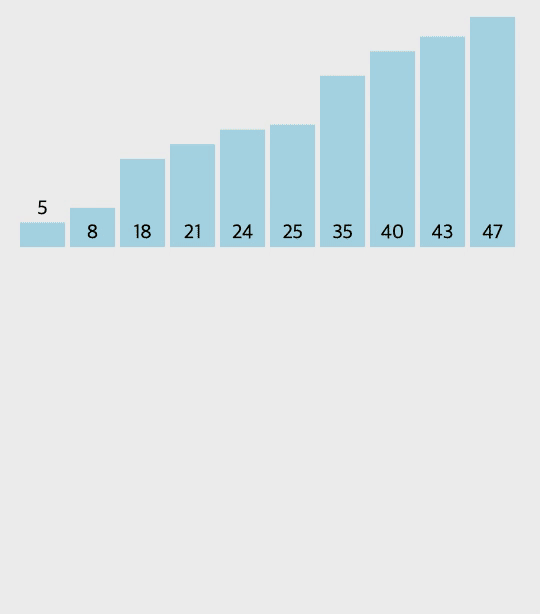
병합 정렬의 과정

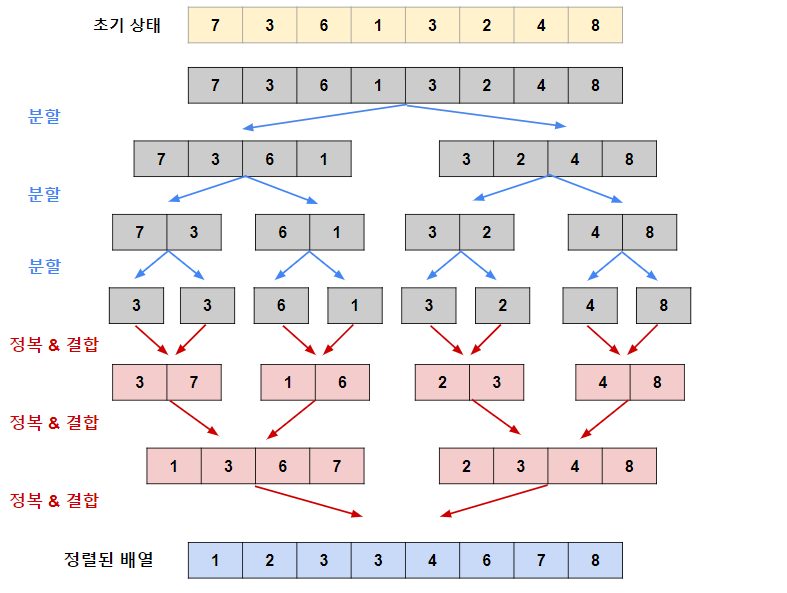
• 분할
  • 주어진 배열의 중간 인덱스를 구함
  • 중간 인덱스를 기준으로 배열을 반토막냄
• 정복
  • 반복해서 반토막을 내다가 마침내 배열의 크기가 0이나 1이 되면 주어진 배열을 답으로 반환함
• 조합
  • 왼쪽 배열과 오른쪽 배열을 인자로 넣어 각각 정렬된 결과를 얻음
  • 양 쪽 배열의 맨 앞으로 비교해 더 작은 수를 찾음
  • 더 작은 수를 꺼내서 새로운 배열에 집어넣음
  • 새로운 배열에 모든 숫자가 들어갈 때까지 반복함

병합 정렬의 특징

• 동일한 값의 원소가 입력에 따라 순서를 보장할 수 있는 안정 정렬임
• 최선과 최악의 경우에도 항상 동일한 시간 복잡도를 가짐
• 주어진 배열 내에서 정렬이 이루어지는 것이 아니라 새로운 배열을 필요로 하기에 제자리 정렬이라고 할 수 없음

자바 구현 코드

public static void mergeSort(int[] arr) {
        sort(arr, 0, arr.length);
    }

    private static void sort(int[] arr, int low, int high) {
        if (high - low < 2) {
            return;
        }

        int mid = (low + high) / 2;
        sort(arr, 0, mid);
        sort(arr, mid, high);
        merge(arr, low, mid, high);
    }

    private static void merge(int[] arr, int low, int mid, int high) {
        int[] temp = new int[high - low];
        int t = 0, l = low, h = mid;

        while (l < mid && h < high) {
            if (arr[l] < arr[h]) {
                temp[t++] = arr[l++];
            } else {
                temp[t++] = arr[h++];
            }
        }

        while (l < mid) {
            temp[t++] = arr[l++];
        }

        while (h < high) {
            temp[t++] = arr[h++];
        }

        for (int i = low; i < high; i++) {
            arr[i] = temp[i - low];
        }
    }

시간 복잡도 & 공간 복잡도

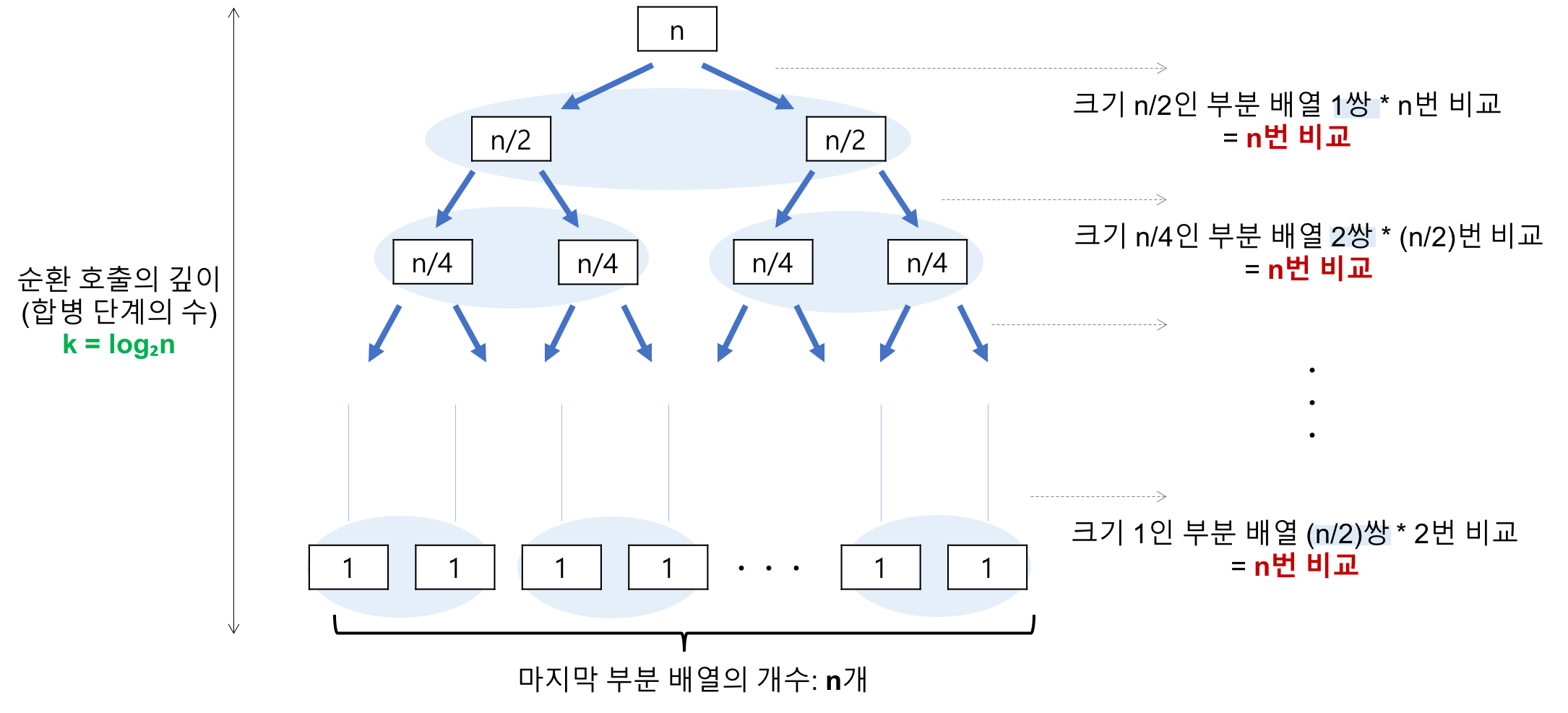
값 비교시에 O(N)의 시간이 소모되고 총 logN번 반복되어야 하므로(반복의 깊이) 총 시간 복잡도는 O(NlogN)임
병합 결과를 담아놓을 배열이 추가로 필요하기에 공간 복잡도는 O(N)임

장단점

• 장점
  • 인풋에 상관없이 안정적인 성능
    • pivot에 따라 성능이 달라지는 퀵 정렬과는 다르게 그냥 반토막을 내기에 인풋에 관계 없이 항상 O(NlogN)을 보장하는 안정적인 알고리즘임
  • 직접 접근이 필요하지 않음
    • 따라서 연결 리스트 형식을 정렬할 때 적합함(순차적인 비교를 통해 정렬하기 때문임)
• 단점
  • O(N)의 추가 공간이 필요함
    • 주어진 배열 자체를 바꾸는 것이 아니라 새로운 배열을 만들어 거기에 순서대로 집어넣어야하기 때문에 추가 공간이 필요함
  • 데이터가 많을 경우 데이터 복사에 상대적으로 시간이 많이 소요됨

참고

https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/MergeSort.md
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
https://www.daleseo.com/sort-merge/
https://propercoding.tistory.com/198
https://velog.io/@eddy_song/merge-sort
https://todaycode.tistory.com/54
https://dongho-dev.tistory.com/1
https://st-lab.tistory.com/233
https://hongcoding.tistory.com/184
https://ittrue.tistory.com/564