정렬을 분할 정복하는 합병 정렬(Merge Sort)

카이사르, 나폴레옹, 손자, 제갈량...

전쟁의 고수들은 모두 이 전략을 사용해서 엄청난 전과를 거뒀다.

누구나 한번쯤 들어봤을 그 전략은 바로 '각개격파'다.

적을 여러 개로 각각 나누어서 분산시킨 다음, (각개各個)
하나씩 하나씩 때려눕힌다는 뜻이다. (격파擊破)

영어로는 'Divide and Conquer' 라고 한다.

'Divide and Conquer' 전략은 전쟁 못지 않게 알고리즘 분야에서도 큰 활약을 한다.
알고리즘 분야에서 굉장히 자주 쓰이고, 그만큼 중요한 테크닉이다.

컴퓨터 공학에서는 'Divide and Conquer'를 직역한 '분할 정복'이라는 말이 쓰인다.

개인적인 취향으로는 각개 격파가 더 잘 와닿지만,
다들 '분할 정복'이라고 부르니까 이 글에서는 분할 정복이라는 말을 쓰도록 하자.

분할 정복(a.k.a 각개격파)이란 무엇일까

분할 정복 방법은 크게 3가지 부분으로 나뉜다.

• 전체 문제를 더 작은 문제로 반복해서 쪼갠다. (분할)
• 충분히 문제가 작아지면 문제를 푼다. (정복)
• 작은 문제의 답을 합쳐서 전체 문제의 답을 도출한다. (조합)

간단하다.

분할 정복 과정을 시각화하면 요런 느낌의 그림이 된다.

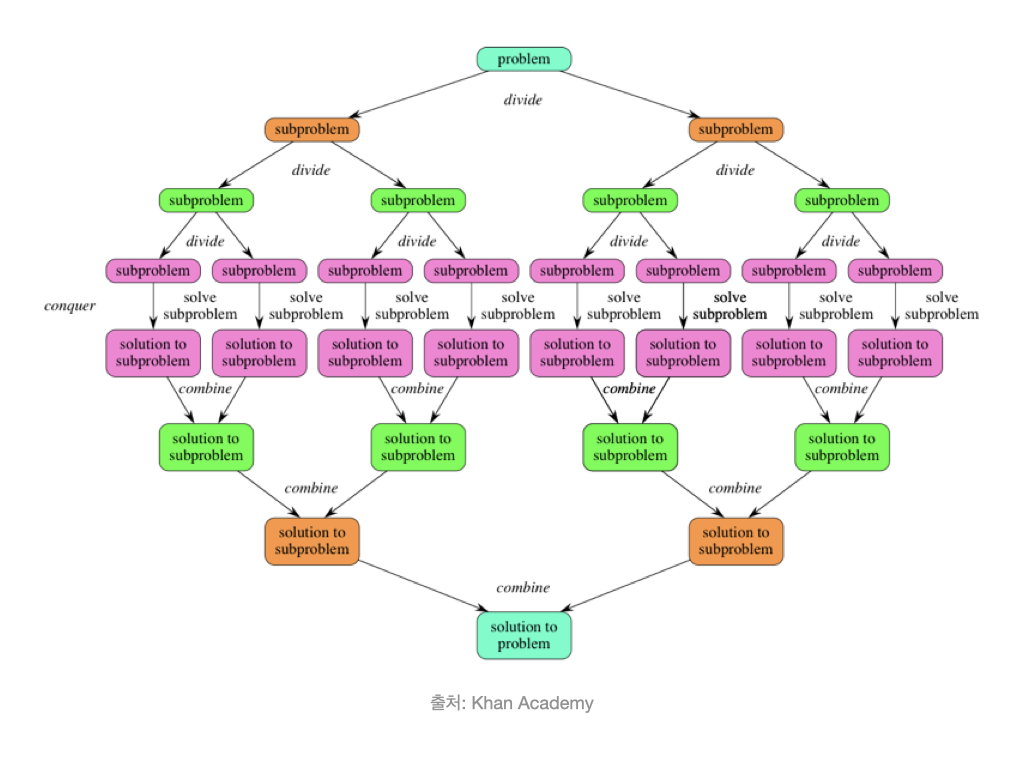
분할 정복은 정렬뿐 아니라,

• 검색 (Binary search),
• 가장 가까운 좌표 찾기 (Closest Pair of Points),
• 큰 수 곱하기(The Karatsuba algorithm),
• 행렬 곱하기(Strassen’s Algorithm)

등등 다양한 문제에 활용된다.

모두 그냥 풀었다면 기하급수적 시간 복잡도가 나오는 문제들이다.
분할 정복은 이 문제들을 선형 로그 시간에 효율적으로 풀 수 있게 해준다.

분할 정복이 왜 효과적인지는 잠시 뒤에 나온다.
그 전에 먼저 합병 정렬을 살펴보자.

정렬 문제를 분할 정복해보자

합병 정렬이 어떻게 분할 정복을 활용하는지 보자.

분할

1. 주어진 배열의 중간 인덱스를 구한다.
2. 중간 인덱스를 기준으로 배열을 반토막 낸다.

정복

3. 반복해서 반토막을 내다가 마침내 배열의 크기가 0이나 1이 된다.
4. 그러면 주어진 배열을 바로 '답'으로 반환한다.

조합

5. 왼쪽 배열, 오른쪽 배열을 인자로 넣어서 각각 정렬된 결과를 얻는다.
6. 양쪽 배열의 맨 앞을 비교해 더 작은 수를 찾는다.
7. 더 작은 수를 꺼내서 새로운 배열에 집어넣는다.
8. 새로운 배열에 모든 숫자가 들어갈 때까지 반복한다.

간단한 코드

def MergeSort(nums):
	
    // 1. 중간 인덱스를 구한다.
    mid = (nums.count) / 2
    
    // 2. 쪼갠 배열을 각각 인자로 넣어서 재귀 호출한다.
    left = mergeSort(0, mid)
    right = mergeSort(mid+1, nums.count)
    
    // 3. 정렬된 2개의 배열을 합친다.
    return merge(left, right)

배열 안의 모든 원소 쪼개기를 반복하면서
결국 1개 혹은 0개로 쪼개진다.

거기서부터 쪼개진 부분 배열들을 합쳐서
다시 정렬된 배열을 만드는 일을 반복한다.

마침내 깔끔하게 정렬된 배열로 다시 탄생하게 된다.

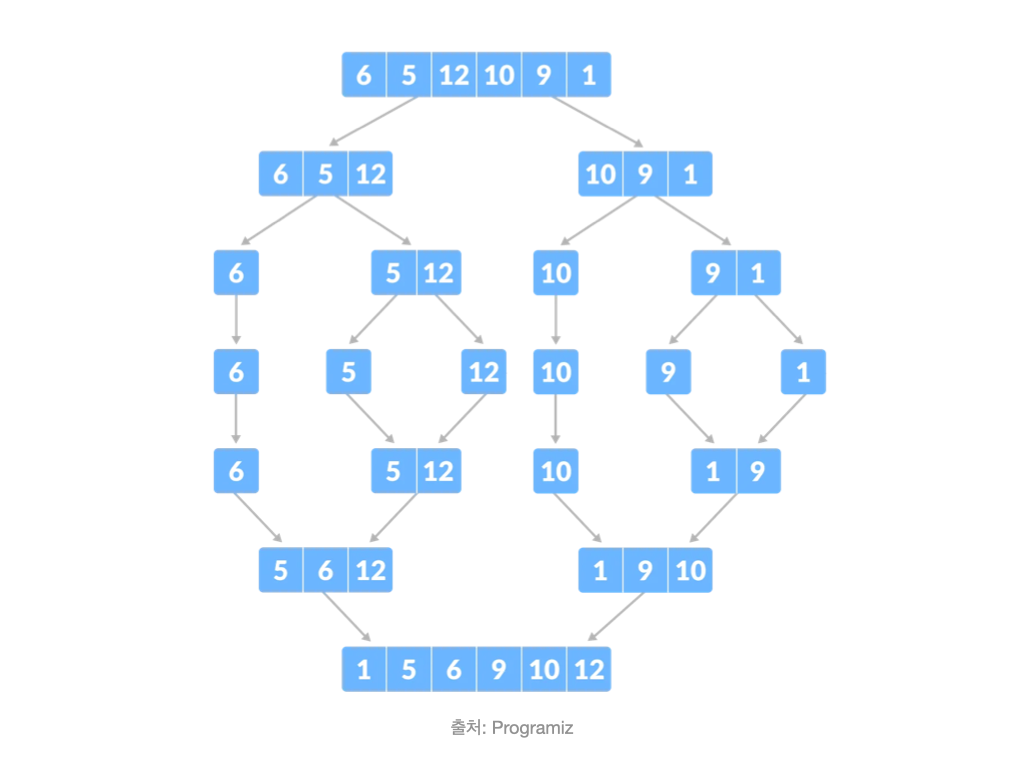
두 배열을 합치는 방법

합병 정렬에서 가장 중요한 부분은
이미 정렬된 두 배열이 주어졌을 때 빠르게 합칠 수 있어야 한다는 것이다.

만약 합치는데도 O(n^2) 작업이 필요하다면 분할 정복은 말짱도루묵이다.

다행히도 이미 정렬된 두 배열이 주어지면, O(n) 작업으로 합칠 수 있다.

새로운 빈 배열을 만든 다음,
양쪽 배열의 앞에서부터 더 작은 쪽을 채워넣으면 된다.

그림으로 표현하면 다음과 같다.
노란색이 주어진 2개의 배열이고, 초록색이 새로운 배열이다.

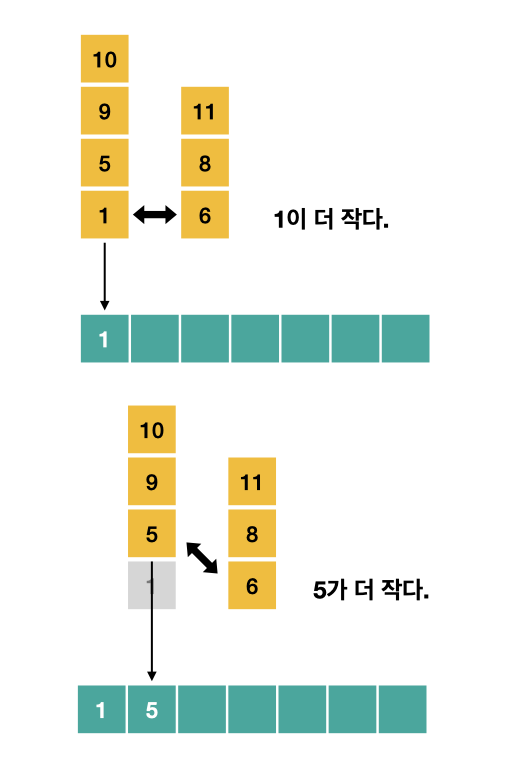
계속 각 배열의 앞쪽을 비교해서 작은 쪽을 채워넣는다.

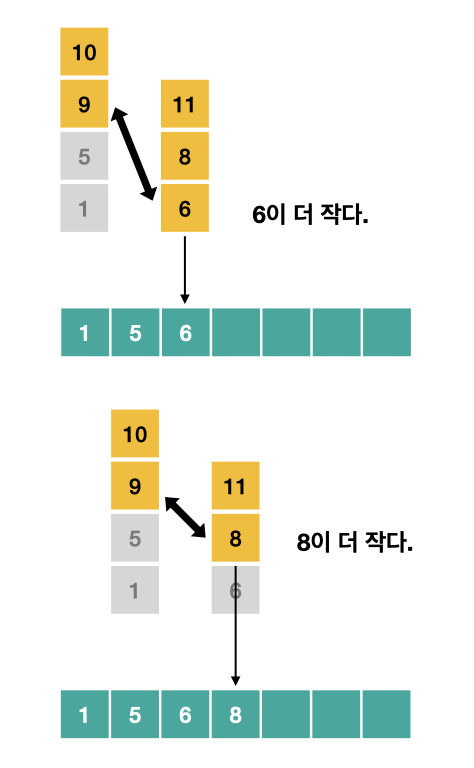
최종적으로는 총 7번의 비교를 거쳐서
길이가 7인 배열이 만들어지게 된다.

이게 합병 정렬의 '합병(Merge)'이다.

합병 정렬의 시간복잡도

합병 정렬의 시간 복잡도는 O(n log n)이다.

분할하는 과정에선 함수 호출만 하기 때문에 신경쓰지 않아도 된다.

정렬된 2개의 배열을 합치는 과정 (조합 단계)에서
양쪽 배열의 길이를 합친만큼 비교 연산을 하게 된다.
따라서 O(n) 작업을 하게 된다.

그렇다면 조합은 총 몇번 하게 될까.

조합은 재귀 호출 횟수만큼 하게 된다.

재귀 호출은 언제까지 하다가 멈추도록 되어있지?
배열이 1개짜리로 줄어들때까지 계속 반토막을 낸다.

전체 문제에서 주어진 배열의 개수가 n이라고 했을 때,
총 몇번을 반토막내야 1이 되는가?

이걸 수식으로 표현해보면

n * (1/2)^x = 1

이걸 정리하면,

x = log n

반토막 내야하는 횟수 x는 'log n'이 된다.

O(n) 작업을 log n번 해야하므로,
시간복잡도는 O(n log n)이 된다.

가장 효율적인 정렬 방법을 달성한 것이다!

이 시리즈의 목적상 합병 정렬의 코드 구현은 따로 적지 않았는데,
필요하다면 링크를 참고하도록 하자.

합병 정렬의 장단점

장점 1. 인풋에 상관없이 안정적인 성능

합병 정렬은 그 어떤 인풋이 들어와도 시간 복잡도가 똑같다.

합병 정렬은 인풋이 얼마나 정렬되어있는지, 어떤 순서로 되어있는지와 상관하지 않는다.
계속 반토막을 낸다.

마지막에 쪼개진 배열을 조합할 때도 O(n) 보다 복잡도가 커지는 일은 없다.

따라서 최악의 인풋이 들어오든, 최고의 인풋이 들어오든 상관없다.

합병 정렬은 어떤 경우에도 O(n log n)을 보장하는 안정적인 알고리즘이다.

장점 2. 직접 접근이 필요하지 않다.

배열(Array)은 인덱스를 통해 데이터의
어떤 요소든 즉각 상수 시간 안에 접근할 수 있다.

이걸 직접 접근, 혹은 비순차 접근(Random access)이라고 한다.

하지만 연결 리스트(Linked list)의 경우는 그게 불가능하다.

연결 리스트 안의 n번째 요소에 접근하려면 시작부터 차례차례 n번 거쳐서 도달해야 한다.

합병 정렬은 다른 정렬 (힙 정렬, 퀵 정렬)과 다르게, 인풋의 자료구조에 '직접 접근'을 하지 않는다.

따라서 연결 리스트를 정렬하는데 적합한 알고리즘이다.

단점 1. O(n)의 추가적인 공간이 필요하다.

합병 정렬의 단점이 하나 있다면
정렬된 두 배열을 조합할 때, 추가적인 공간이 필요하다는 것이다.

주어진 배열 자체를 바꾸는 것이 아니라,
3번째 배열을 만들어서 거기에다 순서대로 집어넣어야 하기 때문이다.

(연결 리스트의 경우는 포인터만 바꾸면 되기 때문에, 추가 공간을 신경 쓰지 않아도 된다.)

분할 정복이 효과적인 이유는?

자 그럼 다시 분할 정복이라는 아이디어로 돌아가보자.
정렬 문제를 이렇게 효과적으로 풀어낼 수 있다니, 궁금해진다.

그런데 어째서 분할 정복을 쓰면 더 좋은 알고리즘이 되는 걸까?
원래 하나의 문제인 걸 나눠서 푼다고 더 빨라지는 이유가 뭐지?

여기에 대한 답은,

문제 크기가 충분히 작아지면,
훨씬 더 간단하게 문제를 풀 수 있기 때문이다.

이게 분할 정복이 가능한 문제의 특징이다.

예를 들어, 정렬해야하는 배열의 크기가 10이라고 해보자.

각각 10개의 원소에 대해서 모두 일대일 비교를 해주어야 한다.
개수가 늘어날수록 작업은 기하급수적으로 늘어날 수 밖에 없다.

하지만 정렬해야하는 배열의 크기가 아주아주 작아서,
들어있는 원소의 개수가 딱 1개라면?

아니 아예 안 들어있는 배열이라면?

[ ] 을 정렬하면 -> [ ]
[1] 을 정렬하면 -> [1]

이건 뭐 이런저런 계산을 할 필요도 없다.
그냥 주어진 배열 자체가 답이다.

왜냐하면 배열의 크기가 0이거나 1일 때는 그 자체로 '정렬된' 배열이기 때문이다.

문제를 작게 쪼개서 문제의 개수가 늘어나더라도,
문제를 푸는 것 자체가 훨씬 쉬워지기 때문에 그 부분을 커버해버린다.

다시 말해 '분할 정복'을 하려면,
부분 문제로 쪼갰을 때 문제 푸는 게 훨씬 더 쉬워져야 한다.

그리고 정렬이 딱 그런 문제다.
정렬에서는 정렬해야할 인풋의 크기가 작을수록 효율성이 기하급수적으로 좋아진다.

합병 정렬은 바로 이 지점을 잘 활용하는 알고리즘이다.

분할 정복을 쓸 수 있는 경우

분할 정복을 쓸 수 있는 조건이 뭐지?
언제 분할 정복을 써도 되는 걸까?

우리의 목표는 정렬 알고리즘을 다시 구현하는 게 아니라,
정렬 알고리즘에 사용된 아이디어를 다시 활용하는 것이다.

그렇다면 어떤 문제에 분할 정복을 사용할 수 있을까?

쉽게 말해, 분할-정복-조합이 가능해야 한다.

1. 분할: 문제를 쪼갰을 때도 전체 문제의 조건이 그대로 유지되어야 한다.
2. 정복: 문제를 최대한 쪼갰을 때, 쉽게 답을 도출할 수 있다.
3. 조합: 부분문제의 답을 합쳐서 전체 문제의 답으로 만들 수 있어야 한다.

분할-정복-조합 순으로 나열했지만,
실제로는 '정복' 그러니까 가장 작게 쪼갠 문제를 어떻게 풀 것인가를 먼저 생각하는 것이 좋다.

어느 순간에 바로 답이 풀리는지를 알아야,
분할과 조합 또한 거기에 맞춰서 생각할 수 있기 때문이다.

분할 정복을 재귀로 구현한다면, 이 부분은 '베이스 조건'이 된다.
무조건 '베이스 조건'부터 생각해야 알고리즘을 쉽게 풀 수 있다.

자세한 내용은 다음 글을 참고하자.

🔗 야, 너두 재귀할 수 있어: 재귀가 풀리는 4단계 접근법

다른 문제에 분할 정복을 적용해보자

자, 그럼 정렬이 아닌 다른 문제를 보고 분할 정복을 적용해보자.

오름차순으로 정렬된 정수 배열 nums와 정수 k가 주어진다. nums안에 중복은 없다.
nums 안에서 k의 인덱스를 찾아라. 없다면 -1을 반환하라.

전형적인 탐색(Search) 문제다.
분할 정복 아이디어를 적용해볼 수 있을까?

문제를 최대한 쪼갰을 때 쉽게 답을 도출할 수 있는가?

YES. 만약 정수 배열 nums의 길이가 1이라면?
우리는 그냥 nums[0]에 뭐가 들어있는지 보고 있으면 0을, 없으면 -1을 리턴하면 된다.
길이가 0이어도 마찬가지. 이때는 무조건 -1이다.

배열 길이가 짧으면 너무나도 간단하게 풀려버린다.

그렇다면 주어진 nums의 길이를 0이나 1이 되도록 쪼개나가면 될 거 같다.

문제를 쪼갰을 때도 조건이 유지되는가?

nums의 길이를 쉽게 쪼개려면 역시 반으로 나누는 게 좋겠다.
그래야 최소한의 분할로 0이나 1에 도달할 테니까 말이다.

근데 부분 문제와 전체 문제가 달라진다면 소용이 없다.

예를 들어, nums를 쪼갰을 때 정렬이 깨진다면?
그러면 분할 정복을 쓸 수가 없다.

하지만 다행히 반으로 쪼갰을 경우,
왼쪽 배열도 정렬된 상태, 오른쪽 배열도 정렬된 상태를 유지한다.

따라서 문제를 쪼갰을 때도 주어진 조건이 유지된다.

부분문제를 합쳐서 전체 답을 만들 수 있는가?

이것도 YES다.

배열을 쪼개서 왼쪽에서 k를 탐색하고, 오른쪽에서 k를 탐색했다고 하자.

왼쪽에서는 -1이 나왔고 (즉, k가 없다)
오른쪽에서는 3이라는 답이 나왔다. (k가 인덱스 3에 있다는 뜻)

그러면 전체 문제의 답은 명확하다.
중복은 없기 때문에 k는 딱 하나의 인덱스에서 나오게 된다.
즉, 오른쪽 배열의 3번째 인덱스가 답이다.

3가지 질문에 답을 했으니 충분히 분할 적용을 적용해
문제를 풀어볼 수 있을 거 같다.

이렇게 분할 정복을 적용해서 특정한 요소를 탐색하는 방법이,
너무나도 유명한 이진 검색(Binary Search)이다.

요약 정리

• 분할 정복은 전체 문제를 작게 쪼개서 푼 다음, 작은 문제의 답을 합쳐서 전체 문제의 답을 도출하는 방법이다.
• 정렬 문제에 분할 정복을 적용해 훨씬 더 효율적으로 만든 알고리즘이 합병 정렬이다.
• 합병 정렬의 시간 복잡도는 인풋에 관계없이 O(n log n)이다.
• 분할 정복이 효과적인 이유 문제 크기가 작아졌을 때 훨씬 더 간단하게 문제를 풀 수 있는 경우가 있기 때문이다.
• 1) 문제를 쪼갰을 때 쉽게 답을 구할 수 있고, 2) 문제를 쪼개도 전체 문제의 조건이 유지되면서, 3) 부분문제의 답을 합쳐서 전체 답을 만들 수 있는 문제라면, 분할 정복을 적용해서 풀어볼 수 있다.