힙 정렬 (Heap Sort)

힙이란?

힙은 완전이진트리 기반 자료구조이다. 최대힙은 부모 노드의 키 값이 자식 노드의 키 값보다 항상 같거나 큰 이진트리를 뜻한다.

index i에 대해서

• 부모 노드의 index : i / 2
• 왼쪽 자식 노드의 index : i * 2 + 1
• 오른쪽 자식 노드의 index : i * 2 + 2
  구조적으로 트리 형식이나 배열로 표현이 가능함!

힙 정렬이란?

힙 정렬이란 최대 힙 트리나 최소 힙 트리를 구성하여 정렬을 하는 방법이다. 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성한다.

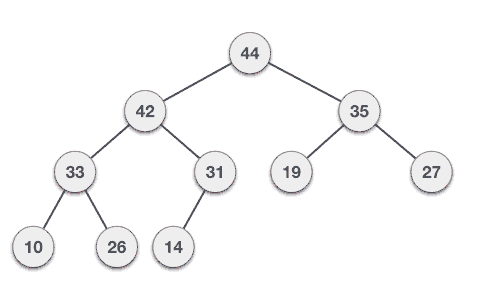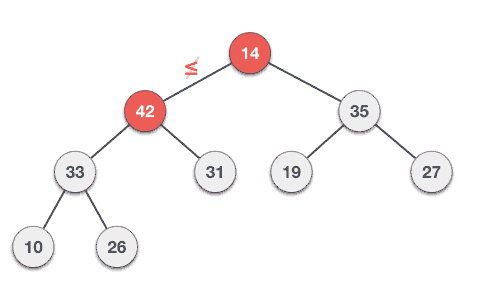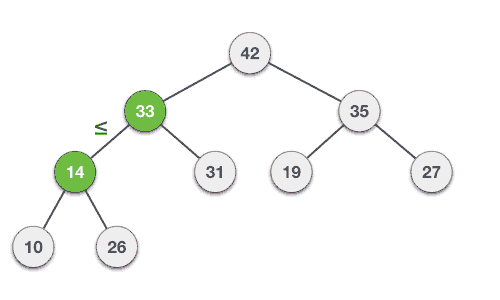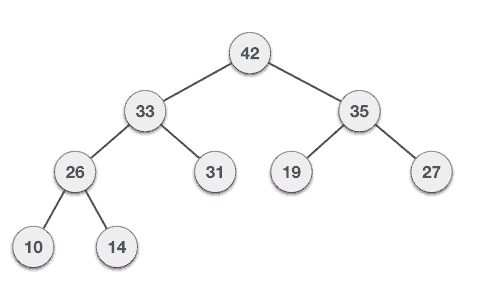
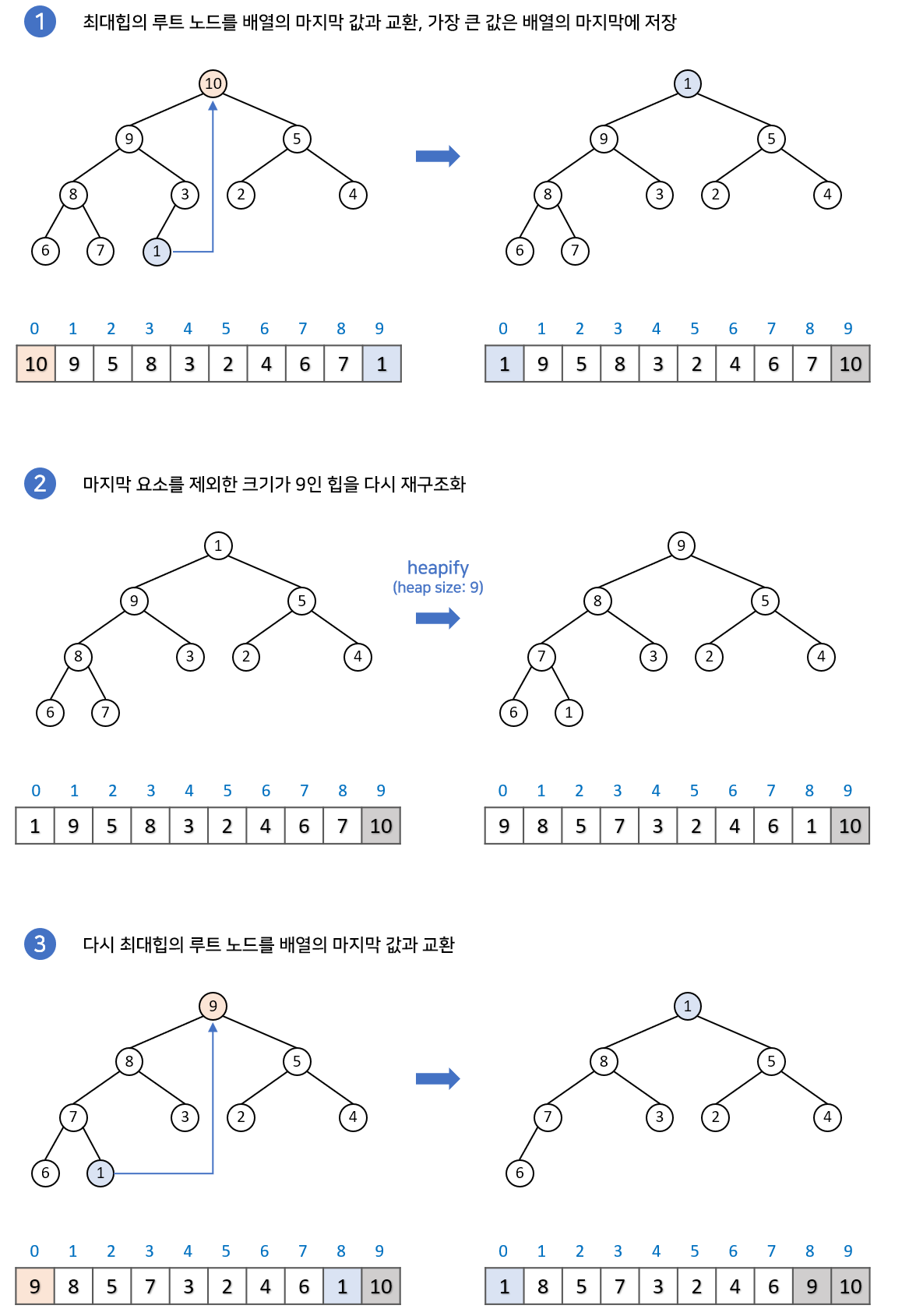
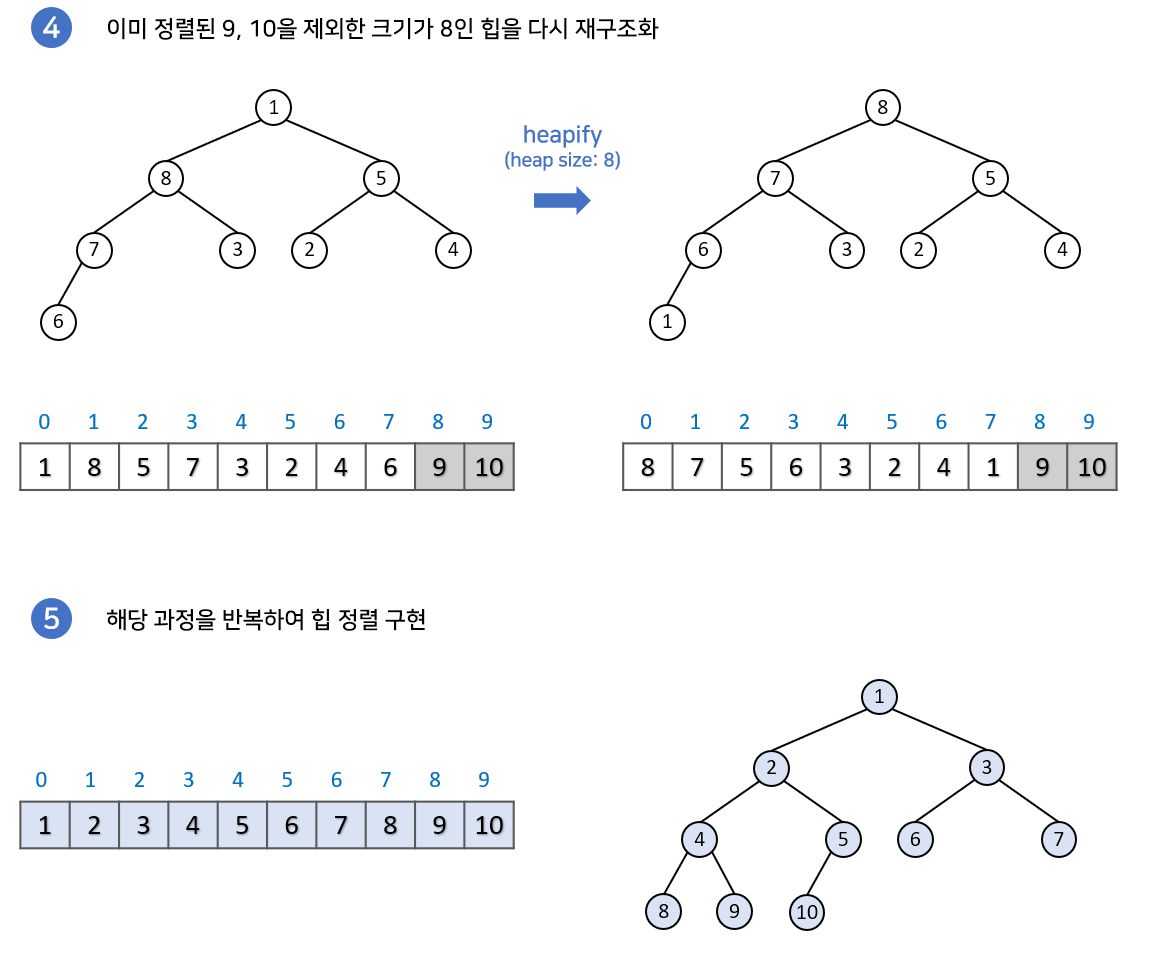
힙 정렬의 과정

1. 배열의 원소를 차례대로 삽입하여 배열을 이진 힙으로 변환함(최대힙을 사용한다고 가정)
2. 힙에서 최댓값을 추출하고 배열의 마지막 원소와 교환함. (이러한 과정을 힙추출이라고 함) 이렇게 추출된 원소는 정렬된 위치에 놓이게 됨
3. 힙 추출 후 힙의 크기를 줄이고 힙의 루트 노드를 다시 최댓값을 만들어줌. (이러한 과정을 힙 복원이라고 함)
4. 2-3단계를 힙의 크기가 1 이하가 될 때까지 반복함.
   

힙 정렬의 특징

• 같은 값의 원소들이 정렬 과정에서 상대적인 순서가 변경될 수 있기에 불안정 정렬임
• 입력 배열 안에서 정렬이 이루어지기에 제자리 정렬이라고 할 수 있음
• 최선, 평균, 최악의 경우 모두 O(NlogN)의 시간 복잡도를 가짐

자바 구현 코드

static void heapSort(int[] arr, int n) {
        //힙구조로 구성 (Build Max-heap) 
        heapify(arr, n);
        
        //루트 제거하고 마지막 요소를 루트로 옮김 (Extract-Max)
        for(int i=n-1; i>=0; i--) {
            swap(arr, 0, i);
            
            heapify(arr, i);
        }
        
    }
    
    //Build Max-heap 
    static void heapify(int[] arr, int last) {    //last변수는 가장 마지막 인덱스를 뜻함
        for(int i=1; i<last; i++) {
            int child = i;
            
            while(child>0) {    
                int parent = (child - 1)/2;
                
                if(arr[child] > arr[parent]) {     //부모와 비교해서 자식이 클경우엔
                    swap(arr, child, parent);    //swap
                }
                child = parent;        
            }
        }
    }
    
    //배열의 요소 두개의 위치를 바꿈 
    static void swap(int[] arr, int idx1, int idx2) {
        int tmp = arr[idx1];
        arr[idx1]=arr[idx2];    //idx1 : idx1 -> idx2
        arr[idx2]=tmp;            //idx2 : idx2 -> idx1
    }

장단점

• 장점
  • 성능이 항상 일관됨
    • 최악의 경우에도 O(NlogN)의 시간 복잡도를 유지하므로 일관된 성능이 요구되는 경우에 적합
  • 메모리 사용량이 적음
    • 추가적인 메모리를 사용하지 않기에 메모리 제약이 있는 사오항에도 사용 가능함
  • 외부 정렬에 적합
    • 디스크와 같은 외부 저장소에 저장된 데이터를 정렬하는 과정에서 사용하면 효율적으로 사용할 수 있음
• 단점
  • 불안정 정렬
    • 같은 값의 원소들의 상대적 순서가 변경될 수 있음.
  • 상대적으로 평균 속도가 느림
    • 퀵 정렬이나 병합 정렬보다 평균 속도가 느림.

참고

https://yozm.wishket.com/magazine/detail/2312/
https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html
https://yjg-lab.tistory.com/169
https://hongcoding.tistory.com/186
https://good-potato.tistory.com/50
https://jino-dev-diary.tistory.com/entry/Algorithm-%EC%A0%95%EB%A0%AC-Heap-Sort-%ED%9E%99-%EC%A0%95%EB%A0%AC
https://moneylogging.tistory.com/entry/%EC%9E%90%EB%B0%94-%ED%9E%99%EC%A0%95%EB%A0%AC
https://velog.io/@eddy_song/heap-sort
https://underdog11.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Heapsort-%ED%9E%99%EC%A0%95%EB%A0%AC
https://velog.io/@emplam27/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-%ED%9E%99%EC%A0%95%EB%A0%ACHeap-Sort
https://m.blog.naver.com/adamdoha/222014528828
https://datamoney.tistory.com/240