Parameter update

while True:
	data_batch = dataset.sample_data_batch()
    loss = network.forward(data_batch)
    dx = network.backward()
    x += - learning_rate * dx

위 코드는 gradient descent 방식을 이용해 weight를 업데이트 한다.
SGD 방식은 적정 weight를 찾기엔 매우 느려서 다른 방식을 찾아봐야 한다.

Momentum update

v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

속도의 원리를 이용해 parameter를 업데이트 해준다. 이때 mu는 종종 0.5, 0.5, 0.99를 사용하고 종종 시간이 지날 수록 0.5 에서 0.99로 변하는 방식으로 이용한다.

AdaGrad update

cache += dx ** 2
x += - learning_rate * dx / (np.sqrt(cache) + 1e-7)

RMSProp update

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + 1e-7)

Adam update

m, v = # ... initialize caches to zeros
for t in xrage(1, big_number):
  dx = # ... evaluate gradient
  m = beta1 * m + (1 - beta1) * dx # update first moment
  v = beta2 * v + (1 - beta2) * (dx**2) # update second moment
  mb = m / (1 - beta1**t)
  vb = v / (1 - beta2**t)
  x += - learning_rate * mb / (np.sqrt(vb) + 1e-7)

Ensemble

1. 복수개의 독립적인 모델들을 학습
2. 결과의 평균을 구함
   -> 2%의 성능 향상이 있음

Regularization (drop out)

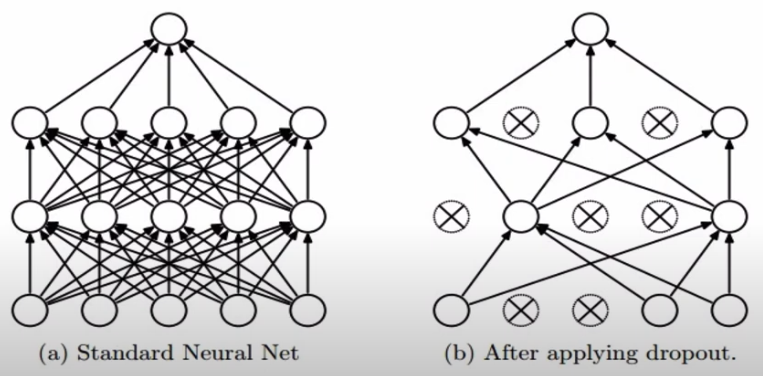
fully neural network와 달리 일부 노드를 0으로 설정함

p = 0.5

def train_step(X):

	H1 = np.maximum(0, np.dot(W1, X) + b1)
    U1 = np.random.rand(*H1.shape) < p # first dropout mask
    H1 *= U1 # drop!
    
    H2 = np.maximum(0, np.dot(W2, H1) + b2)
    U2 = np.random.rand(*H2.shape) < p # second dropout mask
    H2 *= U2 # drop!
    
    out = np.dot(W3, H2) + b3

우리 네트워크는 중복을 가지고 있음

test time에는 다시 p를 곱해줘야 한다. 또는 training time때 p를 나눠줘야 한다.

p = 0.5

def train_step(X):
	H1 = np.maximum(0, np.dot(W1, X) + b1)
    U1 = (np.random.rand(*H1.shape) < p) / p
    H1 *= U1 # drop!
    
    H2 = np.maximum(0, np.dot(W2, H1) + b2)
    U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask
    H2 *= U2 # drop!
    out = np.dot(W3, H2) + b3
    
def predict(X):
	H1 = np.maximum(0, np.dot(W1, X) + b1)
    H2 = np.maximum(0, np.dot(W2, H1) + b2)
    out = np.dot(W3, H2) + b3