트랜스포머 (1/2)

hyeony·2025년 7월 3일

NLP

목록 보기

10/12

1. 트랜스포머(Transformer)의 등장

가. "Attention is all you need" 논문 발표

트랜스포머는 2017년 Google이 발표한 논문인 "Attention is all you need"에서 처음 소개된 모델이다. 이 모델은 기존의 시퀀스-투-시퀀스(seq2seq)의 인코더-디코더 구조를 유지하면서도, 제목처럼 오직 어텐션(Attention) 메커니즘만으로 구현되었다는 특징이 있다.

나. 기존 Seq2seq 모델의 한계 및 RNN 미사용 모델의 등장

기존의 RNN은 단어를 순차적으로 입력받아 처리하는 특성으로 인해 NLP에서 각 단어의 위치 정보(position information)를 가질 수 있어 유용하였다.

그러나 트랜스포머는 RNN을 사용하지 않고 인코더-디코더 구조로 설계되었다. 따라서 단어를 순차적으로 입력받는 방식이 아니므로, 단어의 위치 정보를 다른 방식으로 모델에 알려줄 필요가 있다.

트랜스포머는 이 문제를 포지셔널 인코딩(Positional Encoding)이라는 방법으로 해결한다. 이는 각 단어의 임베딩 벡터에 위치 정보를 더하여 모델의 입력으로 사용하는 방식이다.

다. 번역 성능에서의 우수성

RNN을 사용하지 않았는데도, 트랜스포머는 번역 성능 면에서 기존 RNN 기반 모델보다 우수한 성능을 보여주었다. 이는 NLP 분야에 큰 혁신을 가져왔다.

2. 트랜스포머 기본 구조

가. 인코더-디코더 구조의 유지

앞서 말했듯이, 트랜스포머는 기존 seq2seq 모델의 기본 구조인 인코더-디코더 구조를 그대로 유지한다.

즉, 트랜스포머도 기존 seq2seq와 마찬가지로 인코더에서 입력 시퀀스를 받아들이고, 디코더에서 출력 시퀀스를 생성한다. 이러한 기본적인 틀은 RNN을 사용하지 않음에도 불구하고 계승되고 있다.

나. 인코더와 디코더의 단위 구성 (N개의 층)

트랜스포머의 인코더와 디코더는 단일 층으로 구성된 것이 아니라, 여러 개의 단위가 $N$ 개로 구성되는 반복적인 구조를 가진다.

트랜스포머를 제안한 원 논문에서는, 인코더와 디코더의 개수가 각각 $6$ 개 사용하였다. 이렇게 여러 층을 쌓아올려서 모델의 표현력을 높이고 더욱 복잡한 패턴을 학습할 수 있도록 설계되었다.

3. 포지셔널 인코딩(Positional Encoding)

가. 위치 정보 얻기: Sinusoidal 함수

트랜스포머는 단어의 위치 정보를 얻기 위해 각 단어의 임베딩 벡터에 위치 정보를 더하여 모델의 입력으로 사용한다. 이 방법을 포지셔널 인코딩이라고 부른다.

트랜스포머는 위치 정보를 가진 값을 만들기 위해 사인 함수와 코사인 함수를 사용한다. 이러한 함수를 사용하는 데는 다음과 같은 여러 이점이 있다.

① 고유한 위치 표현

사인 함수와 코사인 함수는 연속적이고 주기적이며 미분 가능한 값을 제공하므로, 입력 시퀀스의 각 위치를 고유하게 표현할 수 있다.

② 상대적 거리 정보 인코딩

두 위치 간의 차이가 위상 변화(phase shift)로 표현되므로, 모델이 명시적인 위치 정보는 몰라도 상대적인 위치 정보를 추론할 수 있다.

③ 부드러운 변화

Sinusoidal 함수는 위치가 증가함에 따라 부드럽게 변하는 값을 생성하는데, 이는 셀프-어텐션(self-attention) 메커니즘이 위치 간의 관계를 자연스럽게 학습하는 데 도움을 준다.

④ 다양한 주파수로 확장성 제공

다양한 주파수로 사인 함수와 코사인 함수를 사용함으로써, 시퀀스 내의 long-range dependencies을 모두 다룰 수 있다.

⑤ 학습 불필요

Sinusoidal Positional Encoding은 고정된 함수 기반으로 설계되므로, 별도의 파라미터를 추가하지 않고도 일반화가 잘 이루어진다. 이는 훈련 중 보지 못한 시퀀스 길이에도 효과적으로 작동하게 한다.

나. 임베딩 벡터와 포지셔널 인코딩의 덧셈

트랜스포머는 위치 정보를 가진 값을 만들어내기 위해 다음 두 개의 함수를 사용한다.

PE_{pos, 2i}=\sin{\frac{pos}{10000^{\frac{2i}{d_{model}}}}}

PE_{pos, 2i+1}=\cos{\frac{pos}{10000^{\frac{2i}{d_{model}}}}}

$pos$ : 입력 문장에서의 임베딩 벡터의 위치
$i$ : 임베딩 벡터 내의 차원의 인덱스
$d_{model}$ : 트랜스포머의 모든 층의 출력 차원을 의미하는 하이퍼파라미터. 임베딩 벡터도 $d_{model}$ 의 차원을 가짐. 논문에서는 $d_{model}=512$

임베딩 벡터와 포지셔널 인코딩의 덧셈은 단어의 임베딩 벡터들이 모여 만들어진 문장 행렬과 포지셔널 인코딩 행렬의 덧셈 연산을 통해 이루어진다.

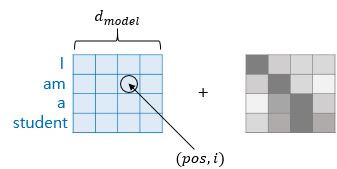
각 임베딩 벡터에 포지셔널 인코딩의 값을 더하는데, 같은 단어라고 하더라도 문장 내 위치에 따라서 트랜스포머의 입력으로 들어가는 임베딩 벡터의 값이 달라진다. 이는 모델이 단어의 의미뿐만 아니라 그 위치 정보도 함께 고려하도록 돕는다.

다. Code Implementation

class PositionalEncoding(tf.keras.layers.layer):
	def __init__(self, position, d_model):
    	super(PositionalEncoding, self).__init__()
        self.pos_encoding = self.positional_encoding(position, d_model)
        
    def get_angles(self, position, i, d_model):
    	angles = 1 / tf.pow(10000, (2 * (i // 2)) / tf.cast(d_model,  tf.float32))
        return position * angles
        
    def positional_encoding(self, position, d_model):
    	angle_rads = self.get_angles(
        position=tf.range(position, dtype=tf.float32)[:, tf.newaxis],
        i=tf.range(d_model, dtype=tf.float32)[tf.newaxis, :],
        d_model=d_model)
        
        # 배열의 짝수 인덱스(2i)에서는 사인 함수 적용
        sines = tf.math.sin(angle_rads[:, 0::2])
        
        # 배열의 홀수 인덱스(2i+1)에서는 코사인 함수 적용
        cosines = tf.math.cos(angle_rads[:, 1::2])
        
        angle_rads = np.zeros(angle_rads.shape)
        angle_rads[:, 0::2] = sines
        angle_rads[:, 1::2] = cosines
        pos_encoding = tf.constant(angle_rads)
        pos_encoding = pos_encoding[tf.newaxis, ...]
        
        print(pos_encoding.shape)
        return tf.cast(pos_encoding, tf.float32)
        
	def call(self, inputs):
		return inputs + self.pos_encoding[:, :tf.shape(inputs)[1], :]

4. 어텐션 메커니즘(Attention Mechanism)

가. 어텐션 함수의 기본 원리

어텐션 함수는 주어진 쿼리(Query)에 대해 모든 키(Key)와의 유사도, 즉, 어텐션 스코어 또는 어텐션 분포를 각각 계산한다. 그리고 이러한 유사도를 어텐션 가중치로 활용하여 키와 매핑된 각각의 값(Value)에 반영한다. 최종적으로 유사도가 반영된 값(Value)을 모두 가중합하여 어텐션 값, 또는 컨텍스트 벡터를 리턴한다.

나. 셀프 어텐션(Self-Attention)의 개념

셀프 어텐션은 말 그대로 어텐션을 자기 자신에게 수행한다는 의미이다. 이는 어텐션 함수에서 사용되는 Query, Key, Value의 출처가 모두 동일한 경우를 말한다. 기존 Seq2seq 모델에서 Q, K, V가 각각 디코더 셀의 은닉 상태나 인코더 셀의 은닉 상태에서 파생되었던 것과 달리, 트랜스포머의 셀프 어텐션에서는 Q, K, V가 입력 문장의 모든 단어 벡터로부터 계산된다.

다. 트랜스포머에서 사용되는 세 가지 어텐션 유형

트랜스포머는 전체 모델 내에서 세 가지 유형의 어텐션을 사용한다. 이들은 모두 멀티 헤드 어텐션(Multi-head Attention)을 수행한다.

① 인코더의 셀프 어텐션

인코더에서 사용되는 셀프 어텐션은 Query, Key, Value가 모두 인코더 벡터에서 파생된다. 인코더의 입력 문장 내의 단어들 간의 연관성을 파악하는 데 사용된다. 이때 패딩 마스크(Padding Mask)가 전달되어 <PAD> 토큰에 대한 유사도 계산을 제외한다.

② 디코더의 마스크드 셀프 어텐션

디코더의 첫 번째 서브층에서 이루어지는 어텐션이다. 이것도 셀프 어텐션으로, Query, Key, Value가 모두 디코더 벡터에서 파생된다.

중요한 차이점은 룩-어헤드 마스크(look-ahead mask)가 적용된다는 점이다. 이는 디코더가 현재 시점의 단어를 예측할 때, 현재 시점보다 미래에 있는 단어들을 참고하지 못하도록 마스킹하는 기능이다. 룩-어헤드 마스크는 패딩 마스크를 포함하도록 구현된다.

③ 디코더의 인코더-디코더 어텐션

디코더의 두 번째 서브층에서 사용된다. 이 어텐션은 셀프 어텐션이 아니며, Query는 디코더의 벡터에서 파생되고, Key와 Value는 인코더의 벡터에서 파생된다. 이는 인코더가 학습한 정보와 디코더가 현재까지 생성한 정보 간의 관계를 학습하는 데 사용되며, 이때도 패딩 마스크가 전달된다.

라. 셀프 어텐션으로 얻을 수 있는 효과

셀프 어텐션은 문장 내의 단어들 간의 연관성을 파악하는 데 뛰어난 능력을 보여준다.

예를 들어, 다음 문장에서

그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤하였기 때문이다.

인간은 그것(it)이 동물(animal)을 가리킨다는 것을 쉽게 알지만, 기계는 그렇지 못하다.

하지만 셀프 어텐션은 입력 문장 내의 단어들끼리 유사도를 계산하여, 그것(it)이 동물(animal)과 연관되었을 확률이 높다는 것을 찾아낸다.

트랜스포머 연구진은 멀티 헤드 어텐션(Multi-head Attention)을 통해, 한 번의 어텐션보다 여러 번의 어텐션을 병렬로 사용하는 것이 더 효과적이라고 판단했다.

이를 통해 각 어텐션 헤드가 서로 다른 시각에서 정보들을 수집할 수 있게 된다. 예를 들어, 첫 번째 헤드는 it과 animal의 연관도를 높게 보고, 두 번째 헤드는 it과 tired의 연관도를 높게 볼 수 있다. 이는 모델이 더 풍부하고 다양한 문맥 정보를 포착하도록 돕는다.

5. 스케일드 닷-프로덕트 어텐션(Scaled Dot-Product Attention)

가. Q, K, V 벡터 얻기

셀프 어텐션을 수행하기 위해, 먼저 각 단어 벡터로부터 쿼리(Q), 키(K), 값(V) 벡터를 얻는 과정이 필요하다.

① 초기 $d_{model}$ 차원 단어 벡터에서 더 작은 차원(예: 64차원)의 Q, K, V 벡터로 변환

셀프 어텐션은 인코더의 초기 입력인 $d_{model}$ 차원을 가지는 단어 벡터들을 직접 사용하는 것이 아니라, 이들로부터 Q, K, V 벡터를 얻는 작업을 먼저 거친다.

여기서 얻은 Q, K, V 벡터는 초기 $d_{model}$ 차원의 단어 벡터보다 더 작은 차원을 가진다. 예를 들어, 논문에서는 $d_model=512$ 차원의 각 단어 벡터를 $64$ 차원을 가지는 Q, K, V 벡터로 변환하였다.

② $d_{model}$ 을 num_heads로 나눈 값을 차원으로 결정

Q, K, V 벡터의 차원은 트랜스포머의 하이퍼파라미터인 num_heads(병렬로 사용할 어텐션 헤드의 수)로 $d_{model}$ 을 나눈 값으로 결정된다.

논문에서는 num_heads를 $8$ 로 지정했으므로, $\frac{512}{8} = 64$ 가 Q, K, V 벡터의 차원이 된다.

③ 가중치 행렬 $(W^Q, W^K, W^V)$ 을 통해 변환

기존 단어 벡터에서 얻은 더 작은 차원의 Q, K, V 벡터는 가중치 행렬을 곱함으로써 완성된다.

이때 사용되는 가중치 행렬 $(W^Q, W^K, W^V)$ 은 각각 $(d_{model}, d_k)$ 또는 $(d_{model}, d_v)$ (여기서 $d_k = d_v = \frac{d_{model}}{ \text{num\_heads} }$ )의 크기를 가지며, 이 가중치 행렬은 훈련 과정에서 학습된다.

즉, $d_{model}=512$ 이고 $\text{num\_heads}=8$ 인 경우, 각 단어 벡터에 $3$ 개의 서로 다른 가중치 행렬을 곱하여 $64$ 차원의 Q, K, V 벡터를 얻어낸다.

나. 스케일링(scaling) 도입

트랜스포머에서는 단순히 두 벡터의 내적을 사용하는 어텐션 함수

\text{score}(q, k) = q · k

가 아니라, 여기에 특정값으로 나누어준 어텐션 함수를 사용한다.

이러한 함수를 스케일드 닷-프로덕트 어텐션(Scaled dot-product Attention)이라고 부른다.

① K 벡터의 차원 $d_k$ 의 제곱근으로 나눔

그 특정 값은 K 벡터의 차원 $d_k$ 에 루트를 씌운 $\sqrt{d_k}$ 이다. 예를 들어, $d_{model}=512$ 일 때 $d_k=64$ 이므로 $\sqrt{64}=8$ 로 나눈다.

이 스케일링은 어텐션 스코어의 값이 너무 커지는 것을 방지하여, Softmax 함수의 어텐션 분포가 극단적으로 $0$ 또는 $1$ 에 치우치는 현상을 완화하는 데 도움을 준다.

다. 어텐션 스코어/분포/값 계산 과정

Q, K, V 벡터를 얻고 스케일링 개념을 적용한 후의 어텐션 메커니즘은 다음과 같은 단계를 거친다.

① 어텐션 스코어 계산

각 Q 벡터는 모든 K 벡터에 대해서 스케일링된 내적 값을 통해 어텐션 스코어를 구한다. 이 어텐션 스코어는 쿼리 단어가 각 키 단어와 얼마나 연관되어 있는지를 보여주는 수치이다.

② 어텐션 분포 계산

어텐션 스코어에 Softmax 함수를 적용하여 어텐션 분포(Attention Distribution)를 구한다. 이 분포는 각 키 단어에 대한 가중치로 사용될 확률 값을 나타낸다.

③ 어텐션 값 계산

어텐션 분포(가중치)를 사용하여 모든 V 벡터를 가중합하여 최종 어텐션 값(Attention Value) 또는 컨텍스트 벡터(Context Vector)를 구한다.

이 과정은 모든 Q 벡터에 대해서 반복된다.

라. 행렬 연산으로 일괄 처리

위의 과정들은 각 Q 벡터마다 개별적으로 연산하는 것이 아니라, 행렬 연산을 사용하여 일괄적으로 계산할 수 있다.

① $Q$ , $K$ , $V$ 행렬을 이용한 스코어 및 값 계산

ⓐ $Q$ , $K$ , $V$ 행렬 얻기:

각 단어 벡터에 개별적으로 가중치 행렬을 곱하는 대신, word embeddings에 가중치 행렬을 곱하여 $Q$ 행렬, $K$ 행렬, $V$ 행렬을 한 번에 구한다.

ⓑ 어텐션 스코어 행렬 계산:

$Q$ 행렬과 $K$ 행렬의 전치(transpose)를 곱한 후( $QK^T$ ), 이 행렬의 각 원소를 $\sqrt{d_k}$ 로 나누어 어텐션 스코어 행렬을 얻는다. 이 행렬의 각 요소는 특정 쿼리 단어와 특정 키 단어 간의 어텐션 스코어 값을 나타낸다.

어텐션 스코어 행렬에 softmax 함수를 적용한 후, $V$ 행렬을 곱하여 각 단어에 대한 어텐션 값을 모두 가지는 어텐션 값 행렬을 최종 결과로 얻는다.

② 행렬 크기 및 연산 결과
ⓐ 입력 문장 행렬:

$(seq\_len, d_{model})$ 크기를 가진다. ( $seq\_len$ 은 입력 문장의 길이)

ⓑ Q, K 행렬:

$(seq\_len, d_k)$ 크기를 가진다.

ⓒ V 행렬:

$(seq\_len, d_v)$ 크기를 가진다 ( $d_k = d_v$ ).

ⓓ 가중치 행렬:

WQ와 WK는 $(d_{model}, d_k)$ 크기, WV는 $(d_{model}, d_v)$ 크기를 가진다.

ⓔ 내적 연산 ( $QK^T$ ) 결과:

$(q\_len, d_k)$ 크기의 $Q$ 행렬과 $(k\_len, d_k)$ 크기의 $K$ 행렬(전치하면 $(d_k, k\_len)$ )을 곱하면, $(q\_len, k\_len)$ 크기의 행렬 $\text{matmul}_{qk}$ 을 얻는다. 여기서 $q\_len$ 은 쿼리 시퀀스 길이, $k\_len$ 은 키 시퀀스 길이이다.

ⓕ 최종 어텐션 값 행렬:
$\text{softmax}(QK^T / \sqrt{d_k})$ (크기: $(q\_len, k\_len)$ )에 $V$ 행렬(크기: $(v\_len, d_v)$ )을 곱하면, 최종 어텐션 값 행렬은 $(q\_len, d_v)$ 크기를 가지게 된다.

<참고 문헌>
유원준/안상준, 딥러닝을 이용한 자연어 처리 입문
https://wikidocs.net/21694
박호현 교수님, 인공지능, 중앙대학교 전자전기공학부, 2024

hyeony

Chung-Ang Univ. EEE.

이전 포스트

RNN Encoder-Decoder

다음 포스트