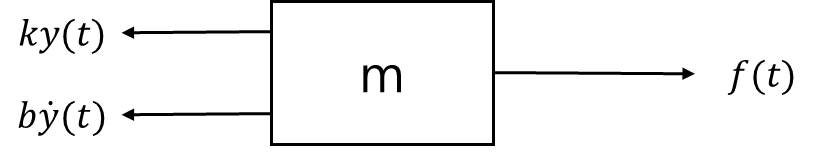5.1 Transfer Function

5.1.1 Transfer Function?

전달 함수란 선형 시스템에서 입력과 출력의 관계를 나타낸다.

앞서 다루었던 선형 상미분 방정식은 다음과 같다.

$\frac{d^ny(t)}{dt^n}+a_{n-1}\frac{d^{n-1}y(t)}{dt^{n-1}}+\cdots+a_1\frac{dy(t)}{dt}+a_0y(t)=b_m\frac{d^mu(t)}{dt^m}+b_{m-1}\frac{d^{m-1}u(t)}{dt^{m-1}}+\cdots+b_1\frac{du(t)}{dt}+b_0u(t)$

위 식의 양변에 대해 초기 조건을 0으로 하여 라플라스 변환을 취하면 다음과 같다.

$s^nY(s)+a_{n-1}s^{n-1}Y(s)+\cdots+a_1sY(s)+a_0Y(s)=b_ms^mU(s)+b_{m-1}s^{m-1}U(s)+\cdots+b_1sU(s)+b_0U(s)$

$\Leftrightarrow (s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0)Y(s)=(b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0)U(s)$

따라서 전달 함수는 다음과 같다.

$\frac{Y(s)}{U(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}$

또한, 전달 함수의 특성은 다음과 같다.
1) 선형 미분 방정식의 전달 함수는 입력의 라플라스 변환에 대한 출력의 라플라스 변환 비율이다.
2) 시스템의 모든 초기 조건은 0이다.
3) 전달 함수는 시스템의 입력에 대해 independent하다.

Example: Find the Transfer function of M.S.D system

여기서 $f(t)$은 입력이고, $y(t)$은 출력이다. F.B.D와 다음과 같고, 이에 대해 뉴턴 제2법칙을 적용하겠다.

$\sum F(t)=ma(t)$

$\Leftrightarrow f(t)-ky(t)-b\dot{y}(t)=m\ddot{y}(t)$

$\Leftrightarrow m\ddot{y}(t)+b\dot{y}(t)+ky(t)=f(t)$

양변에 대해 라플라스 변환을 취하면 다음과 같다. 초기 조건은 0으로 한다.

$ms^2Y(s)+bsY(s)+kY(s)=F(s)$

$\Leftrightarrow (ms^2+bs+k)Y(s)=F(s)$

따라서 전달 함수는 다음과 같다.

$\frac{Y(s)}{F(s)}=\frac{1}{ms^2+bs+k}$

또한, 특성 방정식(characteristic equation)은 다음과 같다.

$ms^2+bs+k=0$

여기서 특성 방정식이란 전달 함수의 분모 다항식을 0으로 설정하여 얻은 방정식을 의미한다.

Definitions of pole and zero
전달 함수가 다음과 같이 정의되었다고 하자.

$\frac{Y(s)}{U(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}=\frac{N(s)}{D(s)}=G(s)$ where $s=\sigma+jw$

여기서 poles은 $D(s)=0$의 근이고, zeros는 $N(s)=0$의 근이다.

Example: Find Poles and zeros of the transfer function G(s)

1) $G(s)=\frac{1}{s+1}$
pole: -1, zero: 無

2) $G(s)=\frac{10(s+2)}{s(s+1)(s+3)^2}$
pole: 0, -1, -3, -3(four poles), zero: -2

5.1.2 Inverse Laplace Transform by partial-fraction expansion

역 라플라스 변환은 다음과 같이 정의된다.

$f(t)=\mathcal{L}^{-1}[F(s)]=\frac{1}{2\pi j}\int_{c-jw}^{c+jw} F(s)e^{st}\, ds$

여기서 $s$는 $F(s)$의 모든 특이점의 실수부보다 큰 실수 상수이다.

그런데 역변환 적분 대신에 부분 분수 전개를 수행한 후 라플라스 변환 표를 이용하여 역 라플라스 변환을 할 수도 있다.

Case 1: 전달함수 $G(s)$의 분모의 근이 모두 실수이고 중근이 없을 때
$G(s)=\frac{5s+3}{s^3+6s^2+11s+6}=\frac{5s+3}{(s+1)(s+2)(s+3)}$

sol 1)
$\Rightarrow G(s)=\frac{a}{s+1}+\frac{b}{s+2}+\frac{c}{s+3}=\frac{a(s^2+5s+6)+b(s^2+4s+3)+c(s^2+3s+2)}{(s+1)(s+2)(s+3)}=\frac{(a+b+c)s^2+(5a+4b+3c)s+(6a+3b+2c)}{(s+1)(s+2)(s+3)}$

$a=-1, b=7, c=-6$

$\therefore G(s)=\frac{-1}{s+1}+\frac{7}{s+2}+\frac{-6}{s+3}$

sol 2)
$(s+1)G(s)=(s+1)(\frac{a}{s+1}+\frac{b}{s+2}+\frac{c}{s+3})=a+(s+1)(\frac{b}{s+2}+\frac{c}{s+3})$

$[(s+1)G(s)]\vert_{s=-1}=a+0\cdot(\frac{b}{s+1}+\frac{c}{s+3})$

$\therefore a=[(s+1)G(s)]\vert_{s=-1}=[(s+1)\frac{5s+3}{(s+1)(s+2)(s+3)}]\vert_{s=-1}=-1$

$b=[(s+2)G(s)]\vert_{s=-2}=\frac{-10+3}{(-2+1)(-2+3)}=7$

$c=[(s+3)G(s)]\vert_{s=-3}=\frac{-15+3}{(-3+1)(-3+2)}=-6$

$\therefore G(s)=\frac{-1}{s+1}+\frac{7}{s+2}+\frac{-6}{s+3}$

Example: Find g(t) of the transfer function

$G(s)=\frac{5s+3}{(s+1)(s+2)(s+3)}=\frac{-1}{s+1}+\frac{7}{s+2}+\frac{-6}{s+3}$

$g(t)=\mathcal{L}^{-1}[G(s)]=\mathcal{L}^{-1}[\frac{-1}{s+1}+\frac{7}{s+2}+\frac{-6}{s+3}]=-e^{-t}+7e^{-2t}-6e^{-3t}$ where $t \ge 0$

5.1.3 Application of the Laplace Transform to the solution of linear ODEs

- First order system

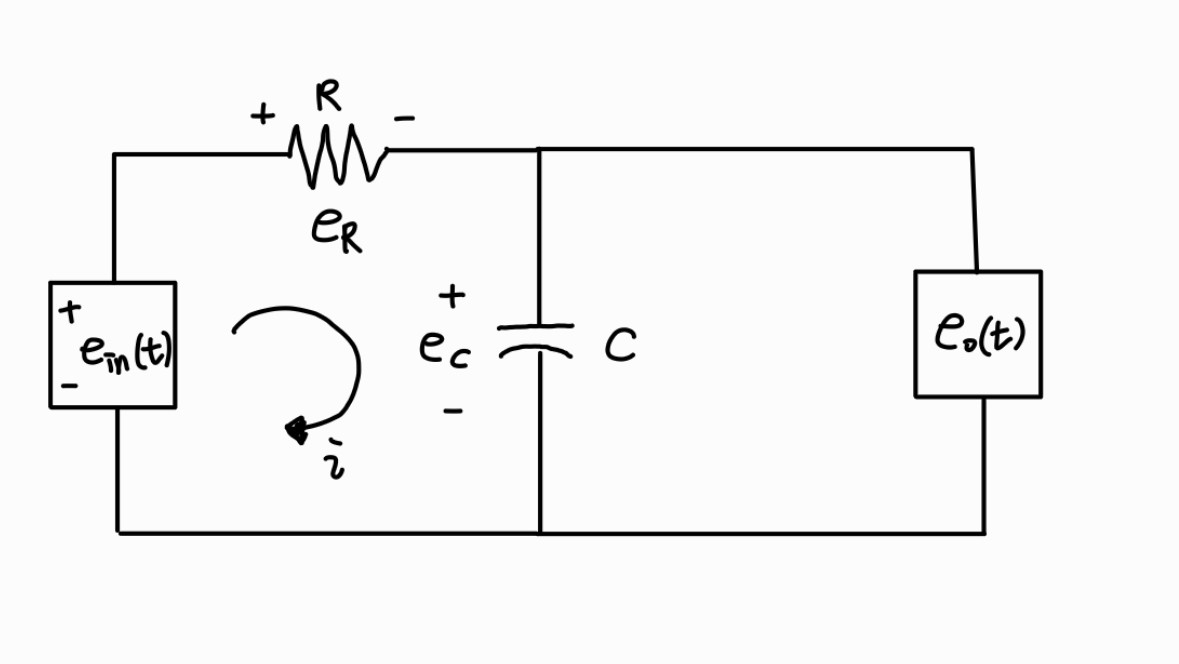
Voltage law에 의해,

$e_{in}(t)=RC\dot{e_o}(t)+e_o(t)$

or $\dot{e_o}(t)+\frac{1}{RC}e_o(t)=\frac{1}{RC}e_{in}(t)$

$y(t)=e_o(t), u(t)=e_{in}(t), \tau=RC$라고 하자.

그러면 $\dot{y}(t)+\frac{1}{\tau}y(t)=\frac{1}{\tau}u(t)$

초기 조건을 0이라고 할 때 양변에 라플라스 변환을 취하면

$sY(s)+\frac{1}{\tau}Y(s)=\frac{1}{\tau}U(s)$

$(\tau s+1)Y(s)=U(s)$

$\Rightarrow Y(s)=\frac{1}{\tau s+1}U(s)$

여기서 전달 함수는 $\frac{1}{\tau s+1}$이다.

한편, 입력을 unit step이라 해보자.

$Y(s)=\frac{1}{\tau s+1}\frac{1}{s}=\frac{\tau}{s+\frac{1}{\tau}}\frac{1}{s}=\frac{a}{s+\frac{1}{\tau}}+\frac{b}{s}=\frac{-1}{s+\frac{1}{\tau}}+\frac{1}{s}$

양변에 역 라플라스 변환을 취하면

$y(t)=\mathcal{L}^{-1}[Y(s)]=\mathcal{L}^{-1}[\frac{1}{s}]-\mathcal{L}^{-1}[\frac{1}{s+\frac{1}{\tau}}]=1-e^{-\frac{1}{\tau}\cdot t}$

위 식은 unit step input과 관련된 first-order system의 응답이다.

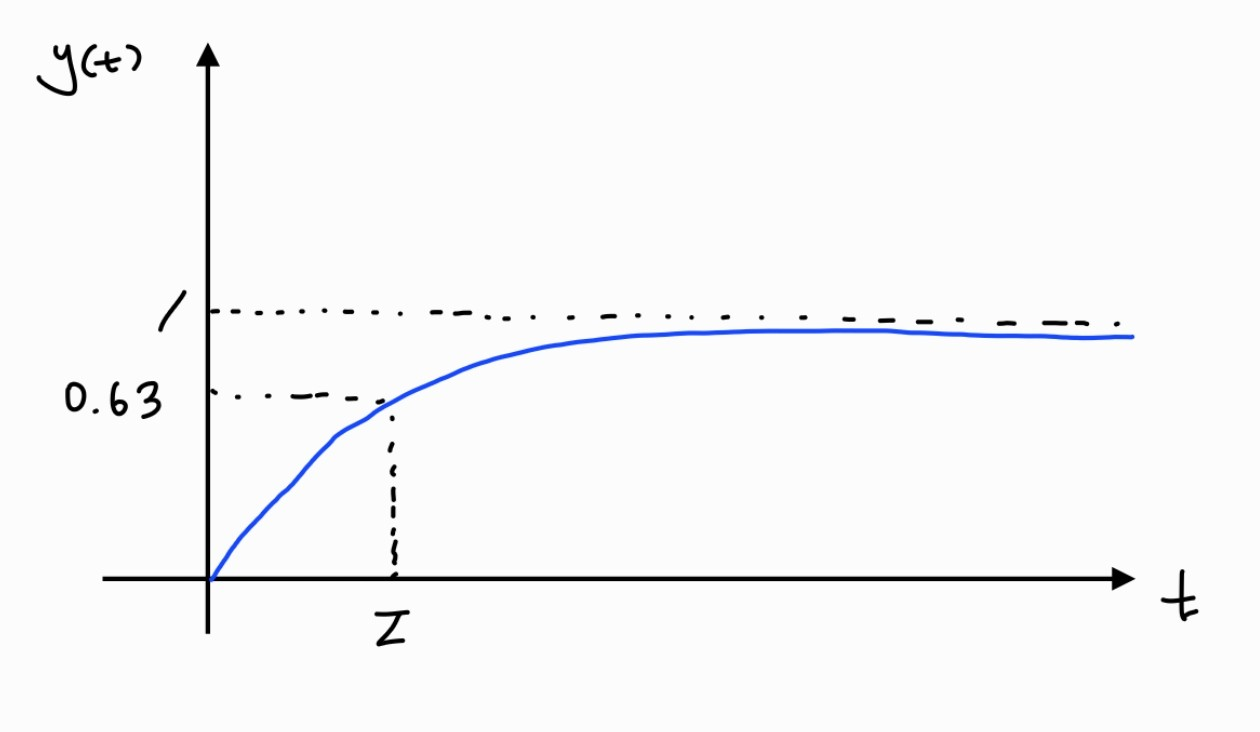
상수 $\tau$은 응답이 최종 값의 63%에 도달하는 데 걸리는 시간이다.

- Second order system

Newton의 법칙에 의해

$m\ddot{x}(t)+b\dot{x}(t)+kx(t)=f(t)$

system parameters와 초기 조건은 다음과 같다.
$m=0.2, b=0.6, k=0.4, x(0)=-1, \dot{x}(0)=2$

$y(t)=x(t), u(t)=f(t)$라 하자. 또한, unit step input에 대해 고려하겠다.

$m\ddot{y}(t)+b\dot{y}(t)+ky(t)=u(t)$

$\Rightarrow 0.2\ddot{y}(t)+0.6\dot{y}(t)+0.4y(t)=u(t)$

$\Rightarrow \ddot{y}(t)+3\dot{y}(t)+2y(t)=5u(t)$

양변에 라플라스 변환을 취하면

$s^2Y(s)-sy(0)-\dot{y}(0)+3sY(s)-3y(0)+2Y(s)=\frac{5}{s}$

$\Leftrightarrow s^2Y(s)+s-2+3sY(s)+3+2Y(s)=\frac{5}{s}$

$\Leftrightarrow (s^2+3s+2)Y(s)+s+1=\frac{5}{s}$

$\Leftrightarrow s(s^2+3s+2)Y(s)+s(s+1)-5=0$

$\Leftrightarrow Y(s)=\frac{-s^2-s+5}{s(s^2+3s+2)}$

위 식을 부분 분수화해보겠다.

$Y(s)=\frac{-s^2-s+5}{s(s+1)(s+2)}=\frac{a}{s}+\frac{b}{s+1}+\frac{c}{s+2}$

$a=[sY(s)]\vert_{s=0}=\frac{-s^2-s+5}{(s+1)(s+2)}\vert_{s=0}=\frac{5}{2}$

$b=[(s+1)Y(s)]\vert_{s=-1}=\frac{-s^2-s+5}{s(s+2)}\vert_{s=-1}=-5$

$c=[(s+2)Y(s)]\vert_{s=-2}=\frac{-s^2-s+5}{s(s+1)}\vert_{s=-2}=\frac{3}{2}$

$\Rightarrow Y(s)=\frac{5}{2s}-\frac{5}{s+1}+\frac{3}{2(s+2)}$

양변에 역 라플라스 변환을 취하면

$y(t)=\mathcal{L}^{-1}[Y(s)]=\frac{5}{2}\mathcal{L}^{-1}[\frac{1}{s}]-5\mathcal{L}^{-1}[\frac{1}{s+1}]+\frac{3}{2}\mathcal{L}^{-1}[\frac{1}{s+2}]=\frac{5}{2}-5e^{-t}+\frac{3}{2}e^{-2t}$

final value$(t\rightarrow\infty)$:
$\therefore y(\infty)=\frac{5}{2}$

※ Final Value Theorem

단, 시스템이 stable하고, final value가 상수여야 한다.

proof)

$\mathcal{L}[\frac{d}{dt}f(t)]=sF(s)-f(0)$

양변에 극한을 취하면,

$\lim_{s\rightarrow0}\mathcal{L}[\frac{d}{dt}f(t)]=\lim_{s \rightarrow 0}sF(s)-f(0)$

한편, 라플라스 변환을 다음과 같이 표현할 수도 있는데

①: $\mathcal{L}[\frac{d}{dt}f(t)]=\int_0^\infty \frac{d}{dt}f(t)e^{-st}dt$

양변에 극한을 취하면,

②: $\lim_{s \rightarrow 0} \mathcal{L}[\frac{d}{dt}f(t)]=\lim_{s \rightarrow 0} \int_0^\infty \frac{d}{dt}f(t)e^{-st}dt=\int_0^\infty\frac{d}{dt}f(t) dt=\lim_{t \rightarrow \infty} f(t) - f(0)$

①, ②에 의해,

$\lim_{s\rightarrow0}sF(s)-f(0)=\lim_{t\rightarrow\infty}f(t)-f(0)$

앞선 예시에 대해 Final Value Theorem을 적용해보면,

$y(\infty)=\lim_{s\rightarrow0}s\frac{-s^2-s+5}{s(s+1)(s+2)}=\frac{5}{2}$

Example: $Y(s)=\frac{1}{s(s+1)}$, $y(\infty)=$?
1) Inverse Laplace transform

$Y(s)=\frac{1}{s}-\frac{1}{s+1}$

$\Leftrightarrow y(t)=1-e^{-t}$

$\therefore y(\infty)=1$

2) Final Value theorem

$y(\infty)=\lim_{s\rightarrow0}sY(s)=\lim_{s\rightarrow0}\frac{s}{s(s+1)}=1$

Example: $Y(s)=\frac{1}{s(s-1)}$, $y(\infty)=$?
1) Inverse Laplace transform

$Y(s)=-\frac{1}{s}+\frac{1}{s+1}$

$\Leftrightarrow y(t)=-1+e^{t}$

$\therefore y(\infty)=\infty$

No final constant value(Not stable)

2) Final Value theorem(Wrong Approach)

$y(\infty)=\lim_{s\rightarrow0}sY(s)=\lim_{s\rightarrow0}\frac{s}{s(s-1)}=-1$