자동제어

Control System이란 에너지, 정보 등 양적인 흐름을 의도하는 방식으로 제어하기 위해 존재하는 모든 시스템을 말한다.\- better stability\- Regulation of output in the presence of disturbances and n

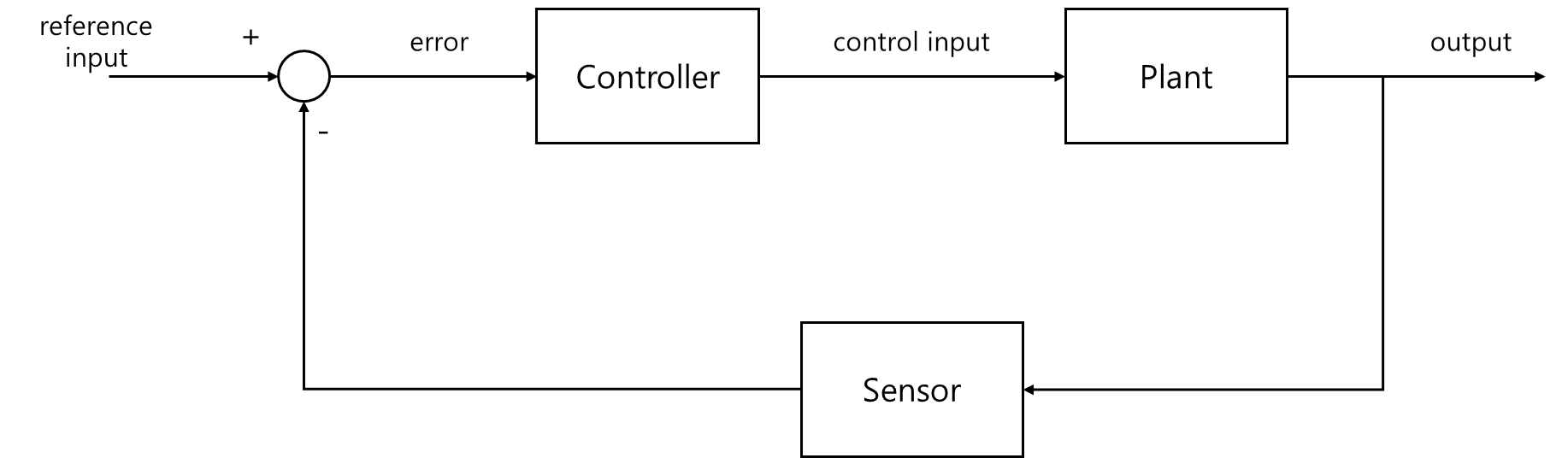
\- 시스템의 dynamic response을 원하는 특성으로 변경\- closed-loop system이 안정적임을 보장\- 허용 가능한 과도 응답(transient response)와 정상 상태 응답(steady-state response) 얻기\- 방해 제거※ 과

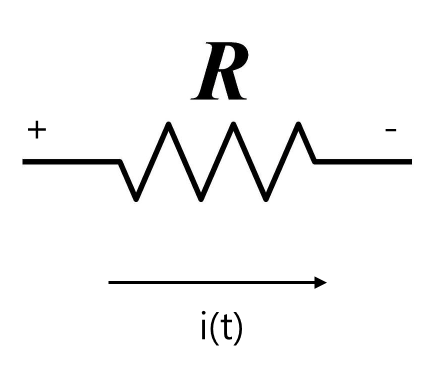
$$e_R(t)=i(t)R$$저항 $$R$$에 걸리는 전압 강하 $$e_R(t)$$는 저항을 흐르는 전류 $$i(t)$$에 비례한다.$$e_L(t)=L\\frac{di(t)}{dt}$$인덕터 $$L$$에 걸리는 전압 강하 $$e_L(t)$$는 인덕터를 흐르는 전류 $$

4.1 Why Linearization? Linearization(선형화) 란 어떤 비선형 시스템을 근사하는 선형 모델을 찾는 과정이다. 대부분 현실 세계의 물리 시스템은 비선형적이다. 그런데 본래 비선형 시스템인 것을 operating point 근처에서 선형화하여

전달 함수란 선형 시스템에서 입력과 출력의 관계를 나타낸다.앞서 다루었던 선형 상미분 방정식은 다음과 같다.$$\\frac{d^ny(t)}{dt^n}+a{n-1}\\frac{d^{n-1}y(t)}{dt^{n-1}}+\\cdots+a_1\\frac{dy(t)}{dt}+a

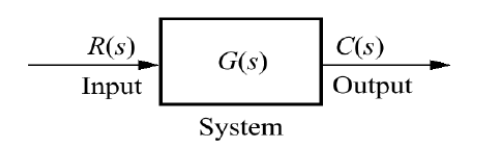
Block Diagram이란 시스템 구조를 설명하는 그래픽 표현이다.$$C(s)=G(s)R(s)$$

시스템은 stable, marginally stable, 또는 unstable할 것이다. 이를 도시하면 다음과 같다.제어 시스템에서 안정성은 필수이다. 왜냐하면 작은 입력으로 하여금 출력을 무한하게 증가시키는 것을 원하지 않기 때문이다.만약 시스템의 입력이 어떤 상수

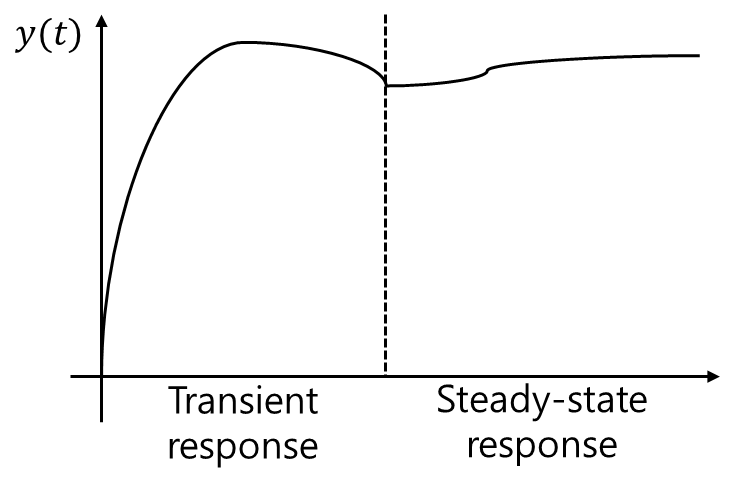
$$y(t)=yt(t)+y{ss}(t)$$$$yt(t)$$: transient response$$y{ss}(t)$$: steady-state responseRecall) steady-state response$$y(\\infty)=\\lim\_{s \\rightarro