Ch 7. Stability of Linear Control Systems

hyeony·2024년 10월 23일
자동제어
0

자동제어

목록 보기
7/8

7.1 Stability of Linear Control Systems

7.1.1 Stability

시스템은 stable, marginally stable, 또는 unstable할 것이다. 이를 도시하면 다음과 같다.

제어 시스템에서 안정성은 필수이다. 왜냐하면 작은 입력으로 하여금 출력을 무한하게 증가시키는 것을 원하지 않기 때문이다.

7.1.2 BIBO(Bounded-input bounded-output) stability

만약 시스템의 입력이 어떤 상수 K1>0K_1>0로 제한되면, BIBO 안정성은 출력도 어떤 상수 K2>0K_2>0로 제한될 것을 보장한다.

※ BIBO stability test in the time domain
1)

y(t)=∫−∞∞h(τ)u(t−τ)dτy(t)=\int_{-\infty}^{\infty}h(\tau)u(t-\tau) d\tau
∣y(t)∣=∣∫−∞∞h(τ)u(t−τ)dτ∣≤∫−∞∞∣h(τ)∣∣u(t−τ)∣dτ≤K1∫−∞∞∣h(τ)∣dτ\vert y(t)\vert=\vert \int_{-\infty}^{\infty}h(\tau)u(t-\tau)d\tau \vert \le \int_{-\infty}^{\infty} \vert h(\tau) \vert \vert u(t-\tau) \vert d\tau \le K_1\int_{-\infty}^{\infty} \vert h(\tau)\vert d\tau
∣y(t)∣<∞⇄∫−∞∞∣h(τ)∣dτ<∞\vert y(t) \vert < \infty \rightleftarrows\int_{-\infty}^{\infty}\vert h(\tau) \vert d\tau<\infty

2)

H(s)=Y(s)R(s)=k(s−z1)(s−z2)⋯(s−zj)(s−p1)(s−p2)⋯(s−pi)H(s)=\frac{Y(s)}{R(s)}=k\frac{(s-z_1)(s-z_2)\cdots(s-z_j)}{(s-p_1)(s-p_2)\cdots(s-p_i)}
=∑i=1nkis−pi i=1,⋯ ,n,j=1,⋯ ,m,m≤n=\sum_{i=1}^n \frac{k_i}{s-p_i}\\ \space i=1,\cdots,n, j=1,\cdots,m,m\le n

양변에 대해 역 라플라스 변환을 취하면

∣h(t)∣=∣∑i=1nkiepit∣≤∑i=1n∣kiepit∣\vert h(t) \vert=\vert \sum_{i=1}^n k_i e^{p_it}\vert\le\sum_{i=1}^n \vert k_ie^{p_it} \vert
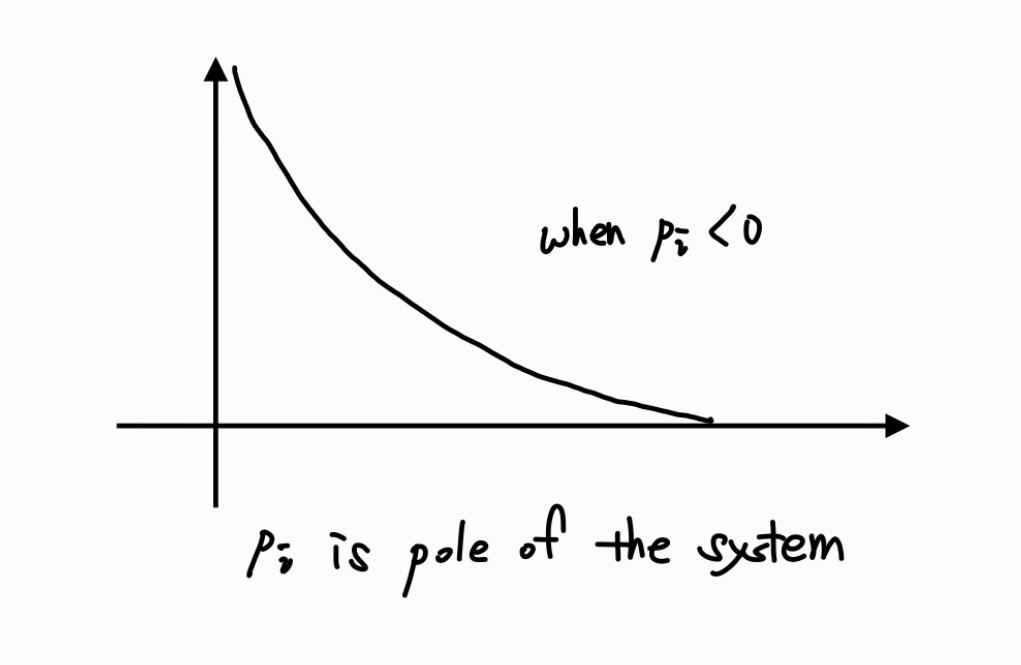
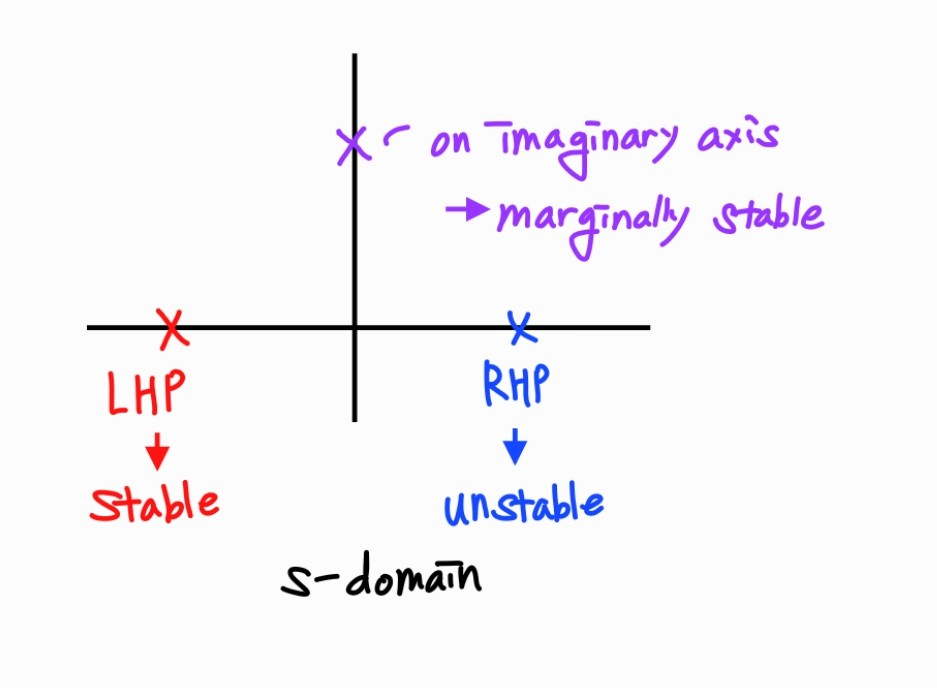
∫−∞∞∣h(τ)∣dτ<∞⇄R(pi)<0\int_{-\infty}^{\infty} \vert h(\tau) \vert d\tau < \infty \rightleftarrows \mathbb{R}(p_i)<0


Example:
1)

T(s)=2s2+3s+2=2(s+1)(s+2)T(s)=\frac{2}{s^2+3s+2}=\frac{2}{(s+1)(s+2)}

poles: s=−1,−2s=-1, -2 → on LHP → stable

2)

T(s)=10s+24s3+2s2−11s−12=10(s+2.4)(s+1)(s−3)(s+4)T(s)=\frac{10s+24}{s^3+2s^2-11s-12}=\frac{10(s+2.4)}{(s+1)(s-3)(s+4)}

poles: s=−1,3,−4s=-1, 3, -4 → 3 on RHP → unstable
모든 poles이 LHP 상에 있어야 stable하다고 할 수 있다.

3)

T(s)=ss2+1T(s)=\frac{s}{s^2+1}

poles: s=±is=\pm i → marginally stable
marginally stable한 경우란 '유한한 임펄스 응답을 가지지만, 일부 입력에 대해 출력이 무한한 경우'을 의미한다. 또한, marginally stable은 unstable 범주에 들어간다.

Summary:
- stable
stable system은 모든 closed-loop poles이 LHP 상에 위치한다.

- unstable
unstable system은 RHP에 적어도 하나의 pole이 있거나, imaginary axis에 중복된 poles이 있는 경우이다.

- marginally stable
marginally stable system은 imaginary axis에 중복되지 않은 pole이 있고, (가능하다면) LHP 상에 pole이 있는 경우이다.

7.1.3 Routh Test

고차 다항식을 인수분해하여 근을 찾는 것은 번거롭고 수치적으로도 적합하지 못하다. 따라서 다른 stability tests로 Routh Test(Routh Hurwitz criterion), Root locus, Nyquist test, Bode plot이 제안된다. 이 중, Routh test은 linear time-invariant system의 완전한 안정성에 관련한 정보를 제공하는 대수적 방법이다.

※ How?
H(s)=b(s)a(s)H(s)=\frac{b(s)}{a(s)}라고 정의하자. 이때 a(s)a(s)은 특성 다항식(characteristic polynomial)이다.

a(s)=ansn+an−1sn−1+⋯+a1s+a0a(s)=a_ns^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0

case 0:
만약 어떤 ana_n이 음수라면, 그 시스템은 unstable하다. 그런데 모든 ana_n이 음수라면 그렇지 않다.

case 1: Form Routh array

--
sns^nana_n an−2a_{n-2} an−4a_{n-4}
sn−1s^{n-1}an−1a_{n-1} an−3a_{n-3} an−5a_{n-5}
sn−2s^{n-2}b1b_1 b2b_2 ⋯\cdots
sn−3s^{n-3}c1c_1 c2c_2 ⋯\cdots
⋯\cdots⋯\cdots
s1s^1j1j_1
s0s^0k1k_1

만약 coefficient가 존재하지 않으면, 0으로 대체한다.

b1=−1an−1∣anan−2an−1an−3∣,b2=−1an−1∣anan−4an−1an−5∣,⋯b_1=\frac{-1}{a_{n-1}}\begin{vmatrix} a_n & a_{n-2} \\ a_{n-1} & a_{n-3} \end{vmatrix}, b_2=\frac{-1}{a_{n-1}}\begin{vmatrix} a_n & a_{n-4} \\ a_{n-1} & a_{n-5} \end{vmatrix}, \cdots
c1=−1b1∣an−1an−3b1b2∣,c2=−1b1∣an−1an−5b1b3∣,⋯c_1=\frac{-1}{b_1}\begin{vmatrix} a_{n-1} & a_{n-3} \\ b_1 & b_2 \end{vmatrix}, c_2=\frac{-1}{b_1}\begin{vmatrix} a_{n-1} & a_{n-5} \\ b_1 & b_3 \end{vmatrix}, \cdots

Routh array의 왼쪽 열에서 부호가 바뀐 횟수는 곧 RHP roots의 개수를 의미한다.

Example: a(s)=s3+s2+2s+8a(s)=s^3+s^2+2s+8

Example - case 0: 모든 계수가 양수이다.

Example - case 1: Routh array

--
s3s^311 22
s2s^211 88
s1s^1−6-6 00
s0s^088
b1=−11∣1218∣=−(8−2)=−6b_1=\frac{-1}{1}\begin{vmatrix} 1 & 2 \\ 1 & 8 \end{vmatrix}=-(8-2)=-6
b2=−11∣1010∣=0b_2=\frac{-1}{1}\begin{vmatrix} 1 & 0 \\ 1 & 0 \end{vmatrix}=0
c1=−1−6∣18−60∣=16(0−(−48))=8c_1=\frac{-1}{-6}\begin{vmatrix} 1 & 8 \\ -6 & 0 \end{vmatrix}=\frac{1}{6}(0-(-48))=8

Routh array 상에서 두 번의 부호 변화가 있었다. 이는 RHP 상에 roots가 두 개 있음을 의미하고, unstable하다.

case 2: If one of the left column entries is zero
이 경우, 0을 ϵ\epsilon으로 대체하고, ϵ→0\epsilon \rightarrow 0으로 한다.

Example: a(s)=s5+2s4+2s3+4s+11s+10a(s)=s^5+2s^4+2s^3+4s+11s+10
Example - case 0: satisfied
Example - case 1:

--
s5s^511 22 1111
s4s^422 44 1010
s3s^3ϵ\epsilon 66 00
s2s^2−12ϵ\frac{-12}{\epsilon} 1010
s1s^166
s0s^01010
b1=−12∣1224∣=−12(4−4)=0b_1=\frac{-1}{2}\begin{vmatrix} 1 & 2 \\ 2 & 4 \end{vmatrix}=-\frac{1}{2}(4-4)=0
b2=−12∣111210∣=−12(10−22)=6b_2=\frac{-1}{2}\begin{vmatrix} 1 & 11 \\ 2 & 10 \end{vmatrix}=-\frac{1}{2}(10-22)=6
c1=−1ϵ∣24ϵ6∣=−1ϵ(12−4ϵ)=−12ϵc_1=\frac{-1}{\epsilon}\begin{vmatrix} 2 & 4 \\ \epsilon & 6 \end{vmatrix}=-\frac{1}{\epsilon}(12-4\epsilon)=\frac{-12}{\epsilon}
c2=−1ϵ∣210ϵ0∣=−1ϵ(−10ϵ)=10c_2=\frac{-1}{\epsilon}\begin{vmatrix} 2 & 10 \\ \epsilon & 0 \end{vmatrix}=-\frac{1}{\epsilon}(-10\epsilon)=10
d1=ϵ12∣ϵ6−12ϵ10∣=ϵ12(10ϵ+72ϵ)=6d_1=\frac{\epsilon}{12}\begin{vmatrix} \epsilon & 6 \\ \frac{-12}{\epsilon} & 10 \end{vmatrix}=\frac{\epsilon}{12}(10\epsilon+\frac{72}{\epsilon})=6
e1=−16∣−12ϵ1060∣=−16(−60)=10e_1=\frac{-1}{6}\begin{vmatrix} \frac{-12}{\epsilon} & 10 \\ 6 & 0 \end{vmatrix}=-\frac{1}{6}(-60)=10

두 번의 부호 변화가 있었으며, 이는 RHP 상에 두 개의 roots가 있음을 의미한다. 따라서 Unstable하다.

case 3:
Routh array에서 어떤 행 전체가 0인 경우가 더러 있다. 이는 다항식이 하나의 인수가 켤레 대칭 근을 가진다는 것을 의미한다.

Routh array에서 어떤 행 si−1s^{i-1} 전체가 0이라고 가정하겠다. 그리고 행 sis^i의 계수는 α1,α2,⋯\alpha_1, \alpha_2, \cdots라 하겠다. auxiliary form은 다음과 같다.

α1si+α2si−2+α3si−4+⋯=0\alpha_1s^i+\alpha_2s^{i-2}+\alpha_3s^{i-4}+\cdots=0

해당 방정식에 대해 미분을 취하고, 0으로 된 행을 방정식의 미분 계수로 대체하면 된다.

Example: a(s)=s4+s3+3s2+2s+2a(s)=s^4+s^3+3s^2+2s+2

case 0: satisfied
case 1:

--
s4s^411 33 22
s3s^311 22 00
s2s^211 22 00
s1s^100 00
s0s^0??
b1=−11∣1312∣=1b_1=\frac{-1}{1}\begin{vmatrix} 1 & 3 \\ 1 & 2 \end{vmatrix}=1
b2=−11∣1210∣=2b_2=\frac{-1}{1}\begin{vmatrix} 1 & 2 \\ 1 & 0 \end{vmatrix}=2
c1=−11∣1212∣=0c_1=\frac{-1}{1}\begin{vmatrix} 1 & 2 \\ 1 & 2 \end{vmatrix}=0

행 s1s^1은 모두 0이다. i−1=1⇔i=2i-1=1 \Leftrightarrow i=2라 할 때,

a1(s)=α1si+α2si−2+α3si−4+⋯=0a_1(s)=\alpha_1s^i+\alpha_2s^{i-2}+\alpha_3s^{i-4}+\cdots=0
s2+2s0=0s^2+2s^0=0

양변에 미분을 취하면

da1(s)ds=2s+0=0\frac{da_1(s)}{ds}=2s+0=0

미분 계수 22으로 기존에 00이라고 쓰여있던 것을 대체한다.

--
s4s^411 33 22
s3s^311 22 00
s2s^211 22 00
s1s^122 00
s0s^022
d1=−12∣1210∣=2d_1=\frac{-1}{2}\begin{vmatrix} 1 & 2 \\ 1 & 0 \end{vmatrix}=2

어떠한 부호 변화도 없기 때문에, RHP 상에는 roots가 존재하지 않는다. roots는 imaginary axis 상에 위치하므로, 이는 marginally stable하다.

7.1.4 2nd order and 3rd order systems

1) 2nd order system

G(s)=1s2+bs+cG(s)=\frac{1}{s^2+bs+c}

case 0: b>0,c>0b>0, c>0

case 1: Routh array

--
s2s^211 cc
s1s^1bb
s0s^0cc
−1b∣1cb0∣=c-\frac{1}{b}\begin{vmatrix} 1 & c \\ b & 0 \end{vmatrix}=c

2nd order system이 stable하면 모든 계수는 양수이다. 또한, 모든 계수가 양수이면, 2nd order system은 stable하다.

2) 3rd order system

G(s)=1s3+as2+bs+cG(s)=\frac{1}{s^3+as^2+bs+c}

case 0: a>0,b>0,c>0a>0, b>0, c>0

case 1: Routh array

--
s3s^311 bb
s2s^2aa cc
s1s^1b−cab-\frac{c}{a} 00
s0s^0cc

3rd order system은 a>0,b>ca,c>0a>0, b>\frac{c}{a}, c>0이면 stable하다.

7.1.5 Controller design using Routh test


Closed-loop transfer function:

T(s)=kG(s)1+kG(s)T(s)=\frac{kG(s)}{1+kG(s)}

특성 방정식은 다음과 같다.

1+kG(s)=0⇔1+ks+1s(s−1)(s+6)=01+kG(s)=0 \Leftrightarrow 1+k\frac{s+1}{s(s-1)(s+6)}=0
⇔s3+5s2+(k−6)s+k=0\Leftrightarrow s^3+5s^2+(k-6)s+k=0

Routh test:
case 0: k>6k>6
case 1: Routh array

--
s3s^311 k−6k-6
s2s^255 kk
s1s^14k−305\frac{4k-30}{5}
s0s^0kk

k>6,k>0,4k−305>0⇔k>7.5k>6, k>0, \frac{4k-30}{5}>0 \Leftrightarrow k>7.5

만약 k>7.5k>7.5이면 Close loop system은 stable하다.

profile
hyeony
Chung-Ang Univ. EEE.
이전 포스트

Ch6. Block Diagrams

다음 포스트

Ch8. Time-domain Performance of Control Systems

0개의 댓글