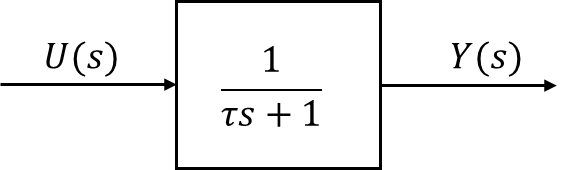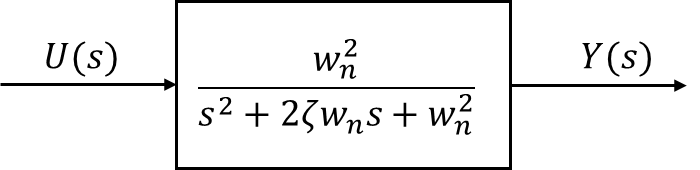8.1 Time-domain Performance of Control Systems
8.1.1 Response
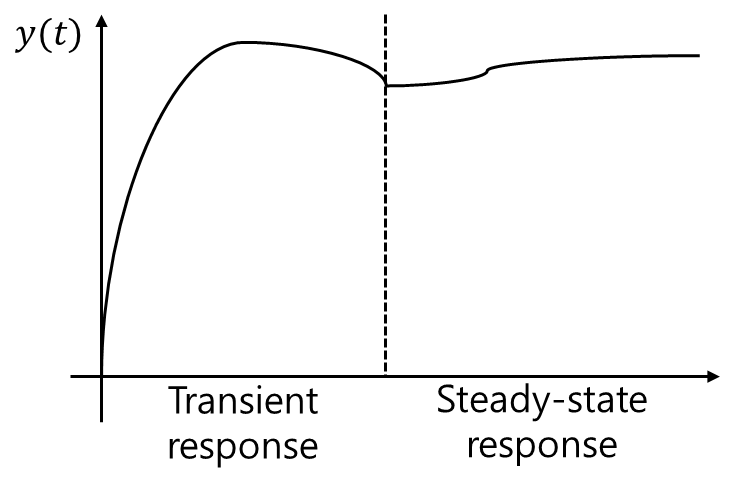
y ( t ) = y t ( t ) + y s s ( t ) y(t)=y_t(t)+y_{ss}(t) y ( t ) = y t ( t ) + y s s ( t ) y t ( t ) y_t(t) y t ( t ) y s s ( t ) y_{ss}(t) y s s ( t )
Recall) steady-state response
y ( ∞ ) = lim s → 0 s G ( s ) U ( s ) y(\infty)=\lim_{s \rightarrow 0} sG(s)U(s) y ( ∞ ) = s → 0 lim s G ( s ) U ( s ) steady-state response 는 시간이 충분히 경과했을 때 출력이 어디에 도달하는 지를 나타내므로 중요하다. 또한, transient response 의 제어는 시스템의 dynamic behavior의 중요한 부분이기 때문에 필수적이다.
※ Unit step response step 은 time domain에서 transient response을 분석할 때 일반적으로 사용되는데, 시스템이 갑작스러운 입력 변화에 얼마나 빠르게 반응하는 지를 잘 보여주기 때문이다.
transfer function의 분모는 항상 1차 또는 2차 형태의 부분 분수로 전개 된다. 따라서 1차/2차 시스템의 step response을 이해하는 것이 중요하다. 참고로 고차 시스템의 response는 1차 and/or 2차 시스템의 response의 합으로 표현된다.
※ 1st order system
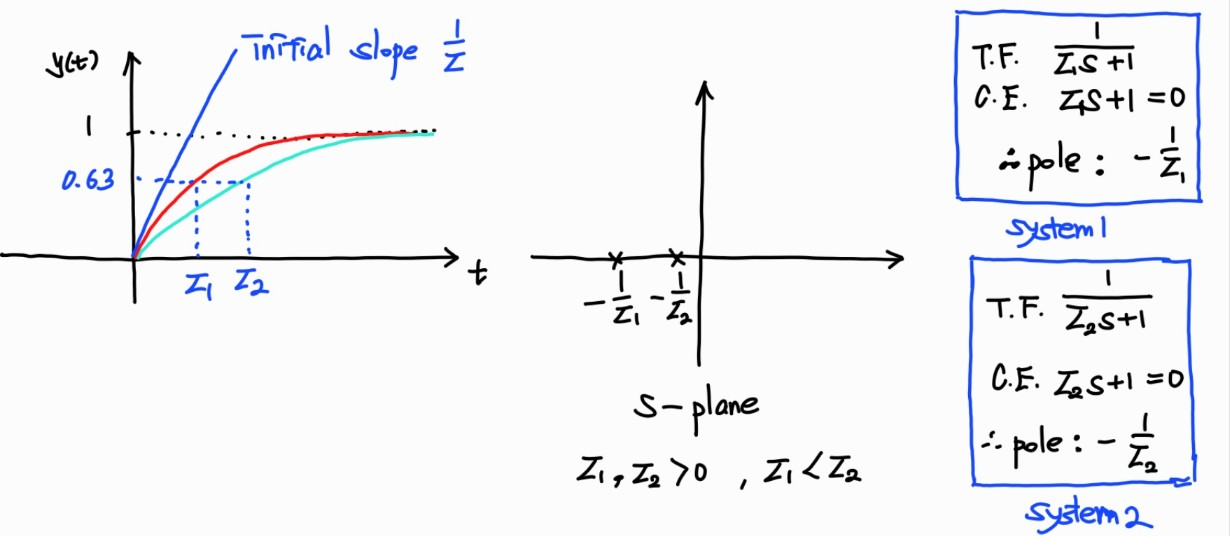
Y ( s ) = 1 τ s + 1 U ( s ) = 1 τ s + 1 1 s = 1 s − τ τ s + 1 Y(s)=\frac{1}{\tau s+1}U(s)=\frac{1}{\tau s+1}\frac{1}{s}=\frac{1}{s}-\frac{\tau}{\tau s+1} Y ( s ) = τ s + 1 1 U ( s ) = τ s + 1 1 s 1 = s 1 − τ s + 1 τ ⇒ y ( t ) = 1 − e − t τ \Rightarrow y(t)=1-e^{-\frac{t}{\tau}} ⇒ y ( t ) = 1 − e − τ t y ( 0 ) = 1 − e 0 = 0 , y ( ∞ ) = 1 − e − ∞ = 1 , y ˙ ( 0 ) = 1 τ y(0)=1-e^0=0, y(\infty)=1-e^{-\infty}=1, \dot{y}(0)=\frac{1}{\tau} y ( 0 ) = 1 − e 0 = 0 , y ( ∞ ) = 1 − e − ∞ = 1 , y ˙ ( 0 ) = τ 1 τ \tau τ τ \tau τ
※ 2nd order system w n w_n w n ζ \zeta ζ ( 0 ≤ ζ < 1 ) (0\le\zeta<1) ( 0 ≤ ζ < 1 )
Unit-step response: Y ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 ⋅ 1 s Y(s)=\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2}\cdot\frac{1}{s} Y ( s ) = s 2 + 2 ζ w n s + w n 2 w n 2 ⋅ s 1
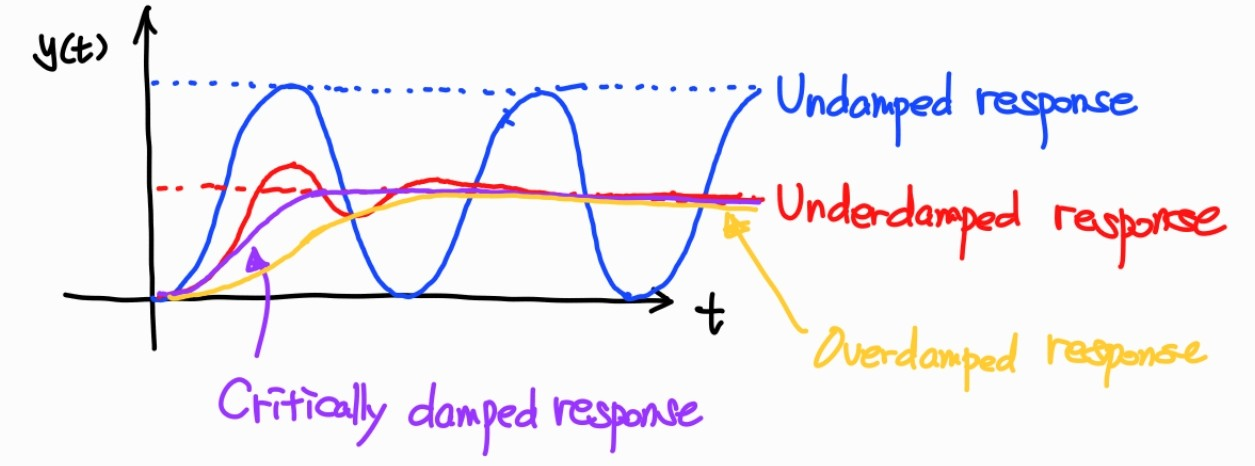
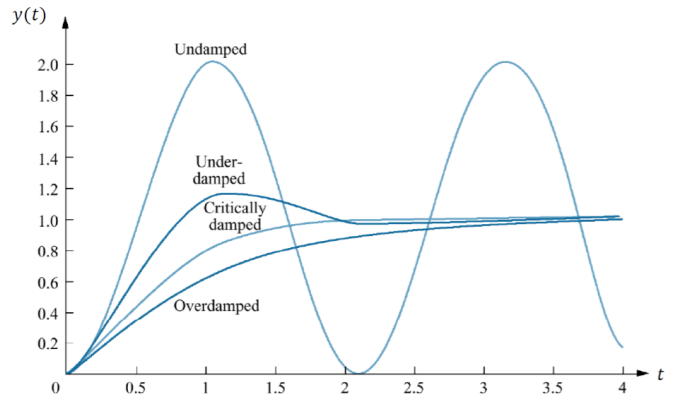
(1) Undamped response(ζ = 0 \zeta=0 ζ = 0
y ( t ) = 1 − cos ( w n t ) y(t)=1-\cos{(w_nt)} y ( t ) = 1 − cos ( w n t ) (2) Underdamped response(0 < ζ < 1 0<\zeta<1 0 < ζ < 1
y ( t ) = 1 − e − ζ w n t 1 − ζ 2 sin ( w d + β ) y(t)=1-\frac{e^{-\zeta w_nt}}{\sqrt{1-\zeta^2}}\sin{(w_d+\beta)} y ( t ) = 1 − 1 − ζ 2 e − ζ w n t sin ( w d + β ) where w d = w n 1 − ζ 2 w_d=w_n\sqrt{1-\zeta^2} w d = w n 1 − ζ 2 tan β = 1 − ζ 2 ζ \tan{\beta}=\frac{\sqrt{1-\zeta^2}}{\zeta} tan β = ζ 1 − ζ 2
(3) Critically damped response(ζ = 1 \zeta=1 ζ = 1
y ( t ) = 1 − e − w n t ( 1 + w n t ) y(t)=1-e^{-w_nt}(1+w_nt) y ( t ) = 1 − e − w n t ( 1 + w n t ) (4) Overdamped response(ζ > 1 \zeta>1 ζ > 1 1st order system
(5) Step response of 2nd order system - Critically damped case(ζ = 1 \zeta=1 ζ = 1
G ( s ) = Y ( s ) U ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 G(s)=\frac{Y(s)}{U(s)}=\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2} G ( s ) = U ( s ) Y ( s ) = s 2 + 2 ζ w n s + w n 2 w n 2 ⇒ G ( s ) = w n 2 s 2 + 2 w n s + w n 2 ( ∵ ζ = 1 ) = w n 2 ( s + w n ) 2 \Rightarrow G(s)=\frac{w_n^2}{s^2+2w_ns+w_n^2}(\because \zeta=1)\\ = \frac{w_n^2}{(s+w_n)^2} ⇒ G ( s ) = s 2 + 2 w n s + w n 2 w n 2 ( ∵ ζ = 1 ) = ( s + w n ) 2 w n 2 Y ( s ) = w n 2 ( s + w n ) 2 ⋅ 1 s = A s + B s + w n + C ( s + w n ) 2 Y(s)=\frac{w_n^2}{(s+w_n)^2}\cdot\frac{1}{s}=\frac{A}{s}+\frac{B}{s+w_n}+\frac{C}{(s+w_n)^2} Y ( s ) = ( s + w n ) 2 w n 2 ⋅ s 1 = s A + s + w n B + ( s + w n ) 2 C A = s Y ( s ) ∣ s = 0 = w n 2 ( s + w n ) 2 ∣ s = 0 = 1 A=sY(s)\vert_{s=0}=\left.\frac{w_n^2}{(s+w_n)^2}\right|_{s=0}=1 A = s Y ( s ) ∣ s = 0 = ( s + w n ) 2 w n 2 ∣ ∣ ∣ ∣ ∣ s = 0 = 1 C = ( s + w n ) 2 Y ( s ) ∣ s = − w n = w n 2 s ∣ s = − w n = − w n C=(s+w_n)^2Y(s)\vert_{s=-w_n}=\left.\frac{w_n^2}{s}\right|_{s=-w_n}=-w_n C = ( s + w n ) 2 Y ( s ) ∣ s = − w n = s w n 2 ∣ ∣ ∣ ∣ ∣ s = − w n = − w n B = d d s ( s + w n ) 2 Y ( s ) ∣ s = − w n = d d s w n 2 s ∣ s = − w n = − w n 2 s 2 ∣ s = − w n = − 1 B=\frac{d}{ds}(s+w_n)^2Y(s)\vert_{s=-w_n}=\frac{d}{ds}\left.\frac{w_n^2}{s}\right|_{s=-w_n}=-\left.\frac{w_n^2}{s^2}\right|_{s=-w_n}=-1 B = d s d ( s + w n ) 2 Y ( s ) ∣ s = − w n = d s d s w n 2 ∣ ∣ ∣ ∣ ∣ s = − w n = − s 2 w n 2 ∣ ∣ ∣ ∣ ∣ s = − w n = − 1 ⇒ Y ( s ) = 1 s − 1 s + w n − w n ( s + w n ) 2 \Rightarrow Y(s)=\frac{1}{s}-\frac{1}{s+w_n}-\frac{w_n}{(s+w_n)^2} ⇒ Y ( s ) = s 1 − s + w n 1 − ( s + w n ) 2 w n ⇒ ∴ y ( t ) = 1 − e − w n t − w n t e − w n t = 1 − e − w n t ( 1 + w n t ) \Rightarrow \therefore y(t)=1-e^{-w_nt}-w_nte^{-w_nt}=1-e^{-w_nt}(1+w_nt) ⇒ ∴ y ( t ) = 1 − e − w n t − w n t e − w n t = 1 − e − w n t ( 1 + w n t ) ※ Transient Response Specification
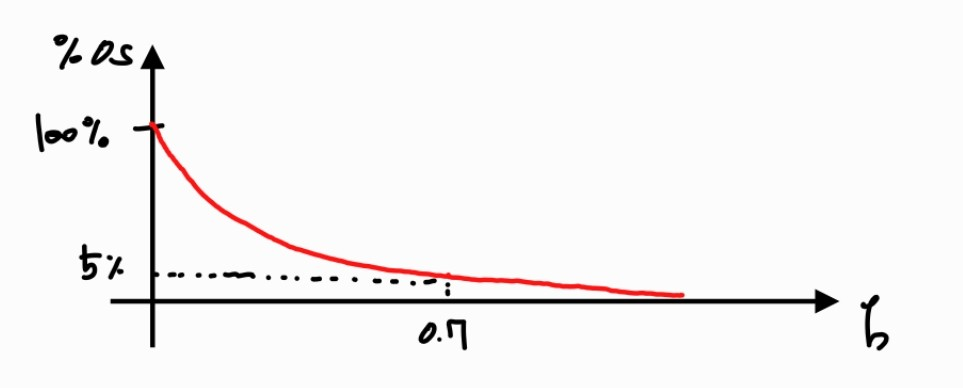
% o v e r s h o o t = y m a x − y f i n a l y f i n a l × 100 % = e − ζ π 1 − ζ 2 × 100 % \% overshoot = \frac{y_{max}-y_{final}}{y_{final}}\times100 \%=e^{-\frac{\zeta\pi}{\sqrt{1-\zeta^2}}}\times100 \% % o v e r s h o o t = y f i n a l y m a x − y f i n a l × 1 0 0 % = e − 1 − ζ 2 ζ π × 1 0 0 % Rise time: t r ≈ 1.8 w n t_r\approx\frac{1.8}{w_n} t r ≈ w n 1 . 8
Peak time: t p = π w d = π w n 1 − ζ 2 t_p=\frac{\pi}{w_d}=\frac{\pi}{w_n\sqrt{1-\zeta^2}} t p = w d π = w n 1 − ζ 2 π
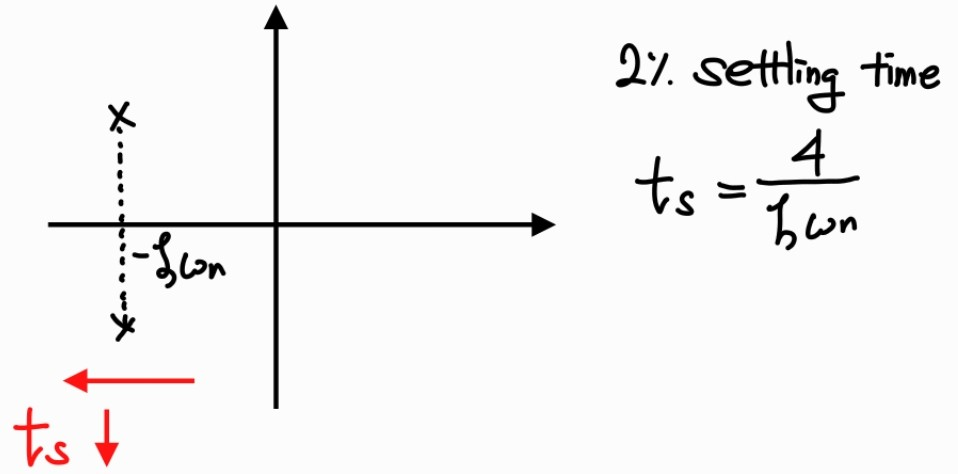
% settling time: 2 % t s ≈ 4 ζ w n 2 \% t_s\approx \frac{4}{\zeta w_n} 2 % t s ≈ ζ w n 4
※ Transient Response specifications for the 2nd order system
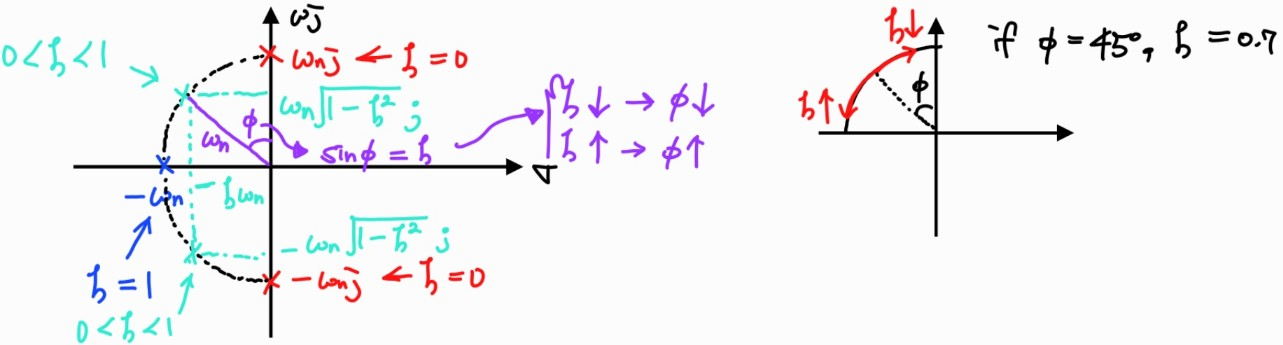
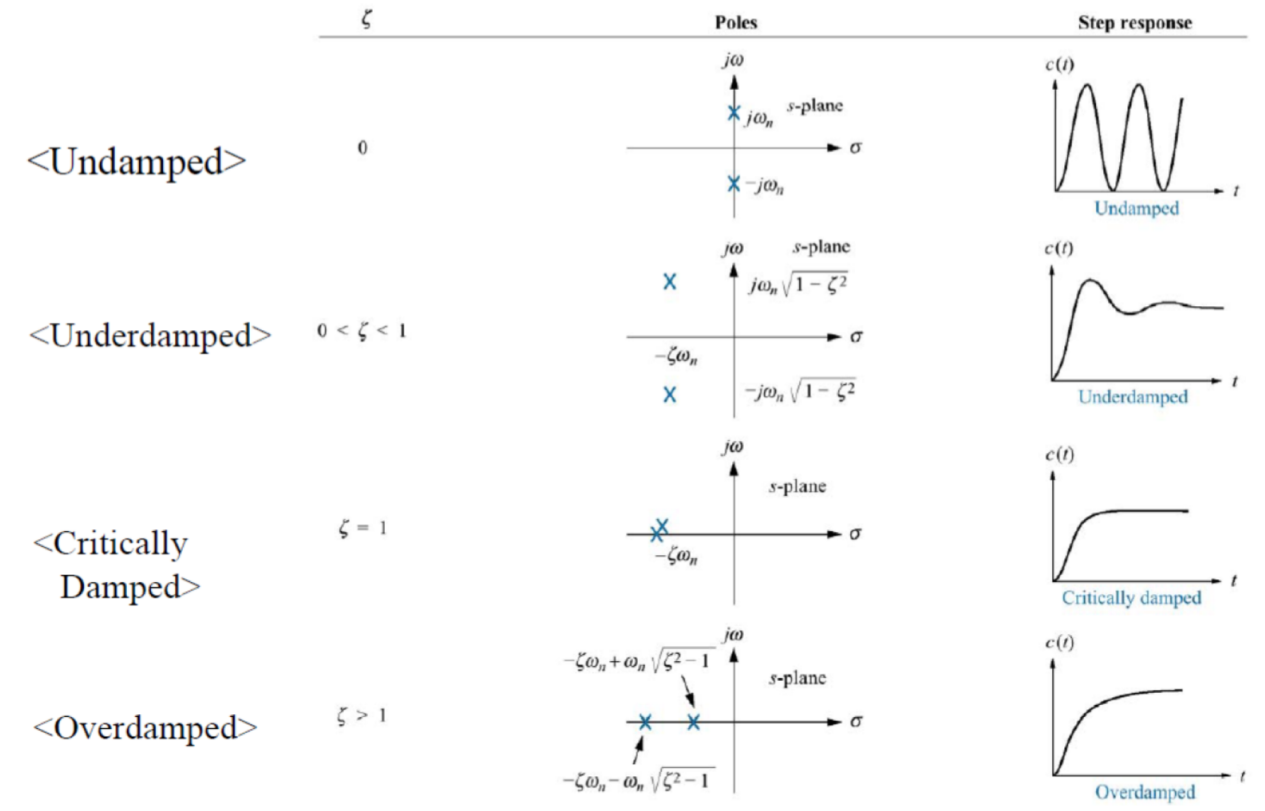
※ Pole locations on s-plane
Y ( s ) U ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 \frac{Y(s)}{U(s)}=\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2} U ( s ) Y ( s ) = s 2 + 2 ζ w n s + w n 2 w n 2 위 함수에서 특성 방정식은 다음과 같다.
s 2 + 2 ζ w n s + w n 2 = 0 s^2+2\zeta w_ns+w_n^2=0 s 2 + 2 ζ w n s + w n 2 = 0 i) ζ = 0 \zeta=0 ζ = 0 s = ± w n j s=\pm w_nj s = ± w n j
ii) ζ = 1 \zeta=1 ζ = 1 s = − w n , − w n s=-w_n, -w_n s = − w n , − w n
iii) 0 < ζ < 1 0<\zeta<1 0 < ζ < 1 s = − ζ w n ± w n 1 − ζ 2 j s=-\zeta w_n\pm w_n\sqrt{1-\zeta^2}j s = − ζ w n ± w n 1 − ζ 2 j
※ Settling time-pole location - For 1st order system
y ( t ) = 1 − e − t τ y(t)=1-e^{-\frac{t}{\tau}} y ( t ) = 1 − e − τ t 1 − e − t s τ = 0.98 ⇔ e − t s τ = 0.02 1-e^{-\frac{t_s}{\tau}}=0.98 \Leftrightarrow e^{-\frac{t_s}{\tau}}=0.02 1 − e − τ t s = 0 . 9 8 ⇔ e − τ t s = 0 . 0 2 ⇔ − t s τ = ln 0.02 ⇔ t s = ln 1 0.02 τ ≈ 4 τ \Leftrightarrow -\frac{t_s}{\tau}=\ln{0.02} \Leftrightarrow t_s=\ln{\frac{1}{0.02}}\tau\approx4\tau ⇔ − τ t s = ln 0 . 0 2 ⇔ t s = ln 0 . 0 2 1 τ ≈ 4 τ - For 2nd order system
※ Unit step responses of the 2nd order system based on damping ratio
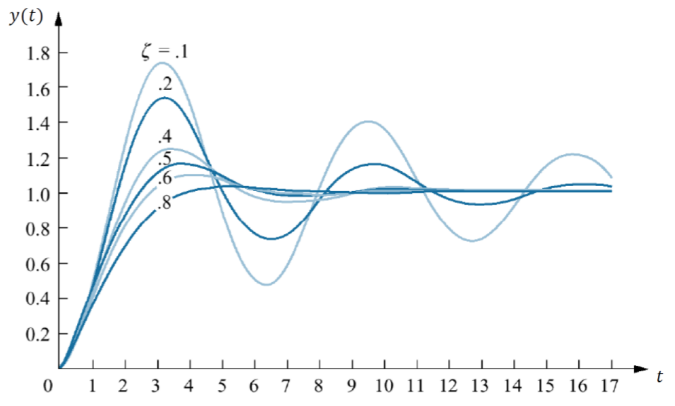
※ Unit step responses of the 2nd order system with various damping ratio
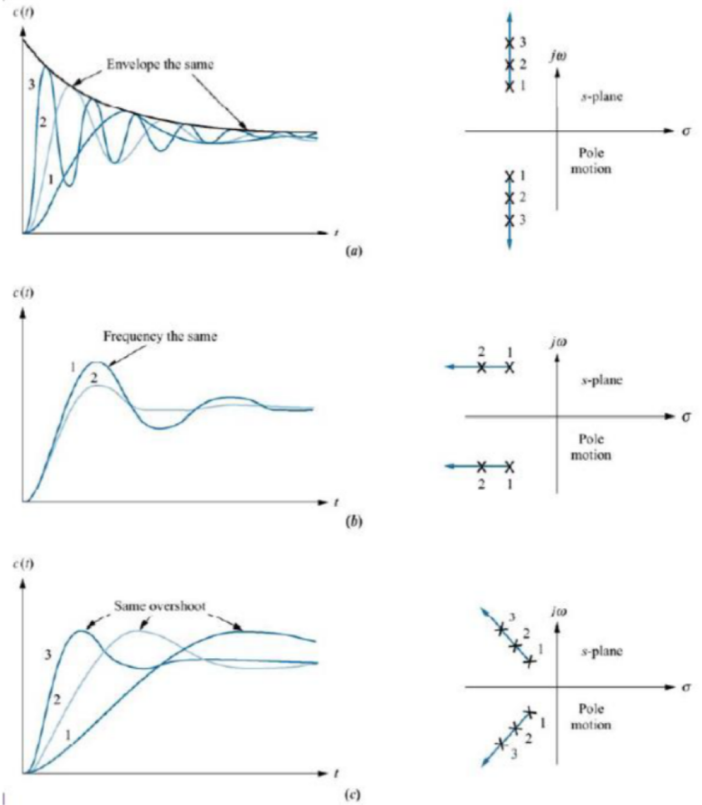
※ Transient responses with respect to pole locations
8.1.2 Dominant Pole
Example)
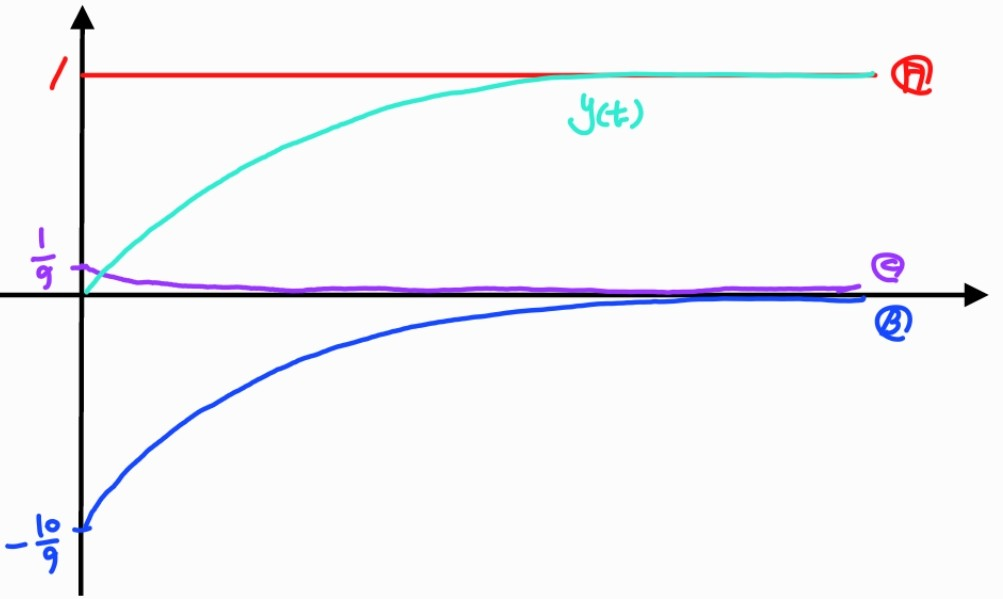
Y ( s ) U ( s ) = 10 ( s + 1 ) ( s + 10 ) , U ( s ) = 1 s \frac{Y(s)}{U(s)}=\frac{10}{(s+1)(s+10)}, U(s)=\frac{1}{s} U ( s ) Y ( s ) = ( s + 1 ) ( s + 1 0 ) 1 0 , U ( s ) = s 1 ⇒ Y ( s ) = 1 s − 10 9 1 s + 1 + 1 9 1 s + 10 \Rightarrow Y(s)=\frac{1}{s}-\frac{10}{9}\frac{1}{s+1}+\frac{1}{9}\frac{1}{s+10} ⇒ Y ( s ) = s 1 − 9 1 0 s + 1 1 + 9 1 s + 1 0 1 ⇒ y ( t ) = 1 − 10 9 e − t + 1 9 e − 10 t \Rightarrow y(t)=1-\frac{10}{9}e^{-t}+\frac{1}{9}e^{-10t} ⇒ y ( t ) = 1 − 9 1 0 e − t + 9 1 e − 1 0 t A ≜ 1 , B ≜ 10 9 e − t , C ≜ 1 9 e − 10 t A\triangleq1, B\triangleq\frac{10}{9}e^{-t}, C\triangleq\frac{1}{9}e^{-10t} A ≜ 1 , B ≜ 9 1 0 e − t , C ≜ 9 1 e − 1 0 t
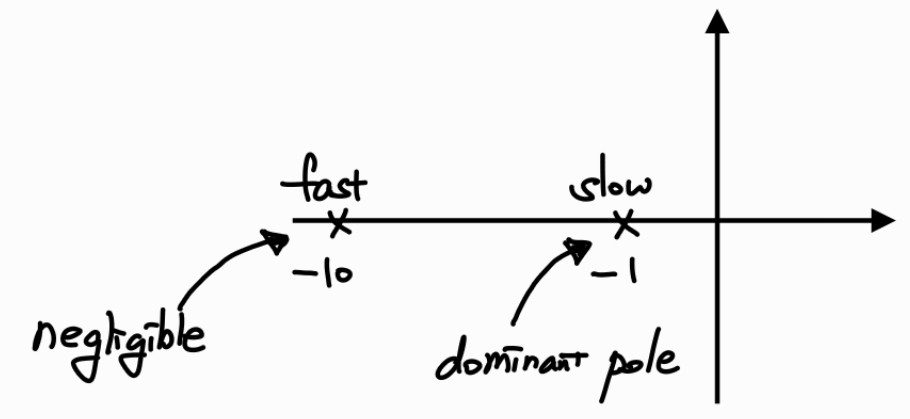
다른 것에 비하면 C C C B B B dominant pole 이라고 한다.
Dominant pole 의 real part 값이 다른 poles보다 충분히 크면, 다른 poles이 total response에 미치는 영향은 무시할 수 있다.
그런데 어느 정도로 커야 dominant라고 간주할 수 있을지에 대해 정량적인 기준이 필요하다. 실제로, pole의 real part 크기가 dominant pole의 크기 보다 최소 5배 ~ 10배 정도 크면, 그 pole은 무시할 수 있다.
8.1.3 Minimum Vs. non-Minimum phase systems
※ Minimum phase system: RHP 상에 zeros 또는 poles의 부재
※ Effect of minimum phase zero U ( s ) = 1 s U(s)=\frac{1}{s} U ( s ) = s 1
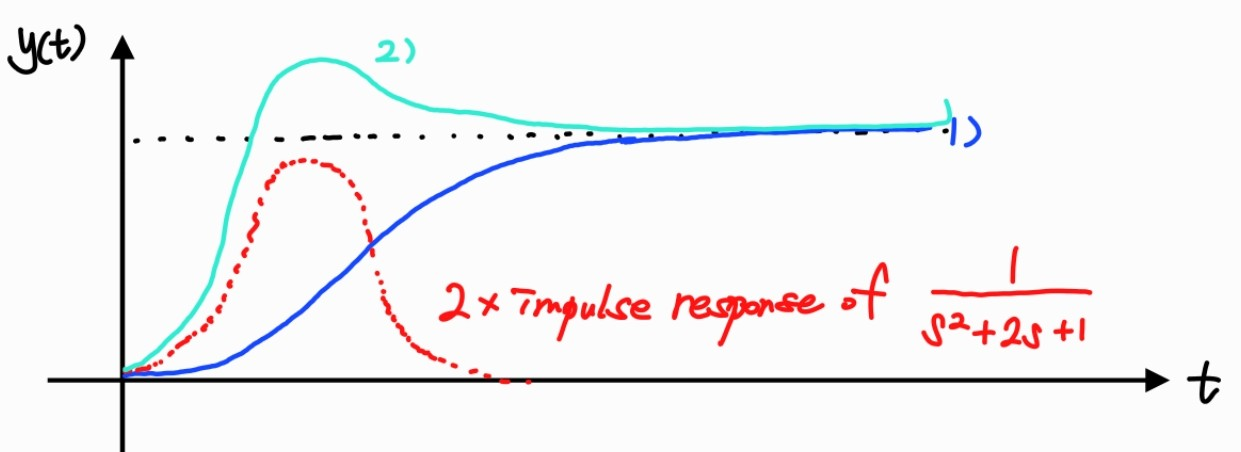
1) Y ( s ) U ( s ) = 1 s 2 + 2 s + 1 ⇒ Y ( s ) = 1 s 2 + 2 s + 1 ⋅ 1 s \frac{Y(s)}{U(s)}=\frac{1}{s^2+2s+1} \Rightarrow Y(s)=\frac{1}{s^2+2s+1}\cdot\frac{1}{s} U ( s ) Y ( s ) = s 2 + 2 s + 1 1 ⇒ Y ( s ) = s 2 + 2 s + 1 1 ⋅ s 1
2) Y ( s ) U ( s ) = 2 s + 1 s 2 + 2 s + 1 ⇒ Y ( s ) = 2 s 2 + 2 s + 1 + 1 s 2 + 2 s + 1 ⋅ 1 s \frac{Y(s)}{U(s)}=\frac{2s+1}{s^2+2s+1} \Rightarrow Y(s)=\frac{2}{s^2+2s+1}+\frac{1}{s^2+2s+1}\cdot\frac{1}{s} U ( s ) Y ( s ) = s 2 + 2 s + 1 2 s + 1 ⇒ Y ( s ) = s 2 + 2 s + 1 2 + s 2 + 2 s + 1 1 ⋅ s 1
- LHP zero는 더 많은 overshoot을 유발한다.
8.1.4 Steady-state error
- open-loop control
G ( s ) = 1 s + 5 , U ( s ) = 3 s G(s)=\frac{1}{s+5}, U(s)=\frac{3}{s} G ( s ) = s + 5 1 , U ( s ) = s 3 Y ( s ) = G ( s ) U ( s ) = 1 s + 5 ⋅ 3 s Y(s)=G(s)U(s)=\frac{1}{s+5}\cdot\frac{3}{s} Y ( s ) = G ( s ) U ( s ) = s + 5 1 ⋅ s 3 By Final Value Theorem
lim s → 0 s Y ( s ) = 3 5 = 0.6 \lim_{s\rightarrow0}sY(s)=\frac{3}{5}=0.6 s → 0 lim s Y ( s ) = 5 3 = 0 . 6 Steady-state error:
3 − 0.6 = 2.4 3-0.6=2.4 3 − 0 . 6 = 2 . 4 - feedback control
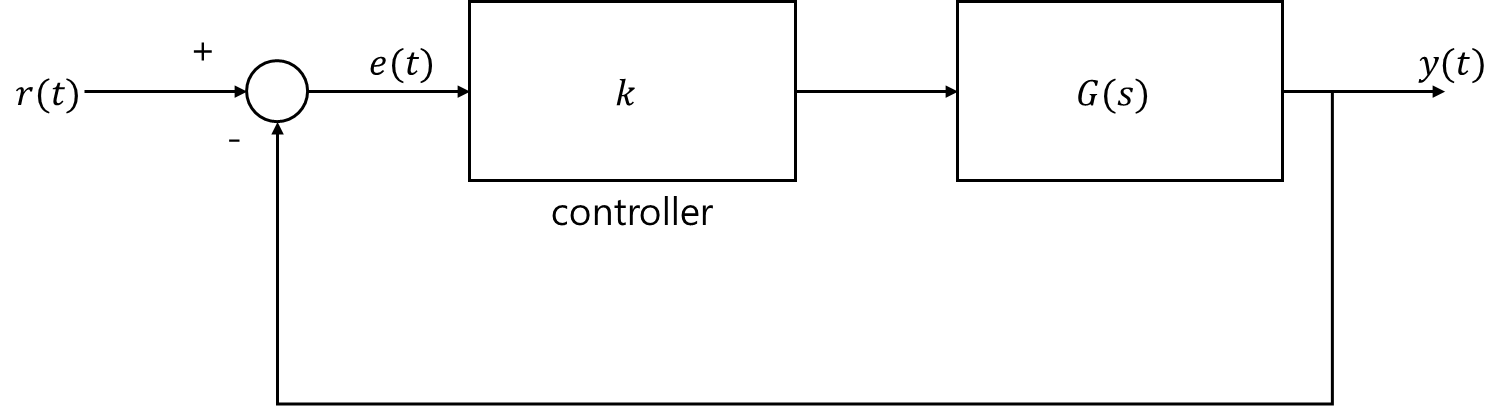
e ( t ) = r ( t ) − y ( t ) e(t)=r(t)-y(t) e ( t ) = r ( t ) − y ( t ) E ( s ) = R ( s ) − Y ( s ) = R ( s ) − k G ( s ) E ( s ) E(s)=R(s)-Y(s)=R(s)-kG(s)E(s) E ( s ) = R ( s ) − Y ( s ) = R ( s ) − k G ( s ) E ( s ) ⇔ E ( s ) = 1 1 + k G ( s ) R ( s ) \Leftrightarrow E(s)=\frac{1}{1+kG(s)}R(s) ⇔ E ( s ) = 1 + k G ( s ) 1 R ( s ) Steady-state error:
e s s = lim s → 0 s E ( s ) = lim s → 0 s 1 1 + k 1 s + 5 3 s = 0.1 ( k = 145 ) e_{ss}=\lim_{s\rightarrow0}sE(s)=\lim_{s\rightarrow0}s\frac{1}{1+k\frac{1}{s+5}}\frac{3}{s}=0.1(k=145) e s s = s → 0 lim s E ( s ) = s → 0 lim s 1 + k s + 5 1 1 s 3 = 0 . 1 ( k = 1 4 5 )