선형 회귀 모델
머신러닝의 가장 큰 목적은 실제 데이터를 바탕으로 모델을 생성해서 만약 다른 입력 값을 넣었을 때 발생할 아웃풋을 예측하는 데에 있다.
이때 우리가 찾아낼 수 있는 가장 직관적이고 간단한 모델은 선(line)이다. 그래서 데이터를 놓고 그걸 가장 잘 설명할 수 있는 선을 찾는 방법을 선형회귀(Linear Regression) 분석이라 부른다.
선형 회귀 모델은 지도 학습 알고리즘으로 주로 수치 예측 문제에 사용한다.
즉, 독립변수(x)를 이용해서 숫자인 종속변수(y)를 예측하는 모델이다.
선형회귀는 독립변수 x와 종속변수 y 사이의 관계를 모델링하여 선형식을 이용해 설명한다.
선형 회귀는 수치 예측 문제에 사용하기 때문에 예측 문제와 추론 문제에 사용한다.
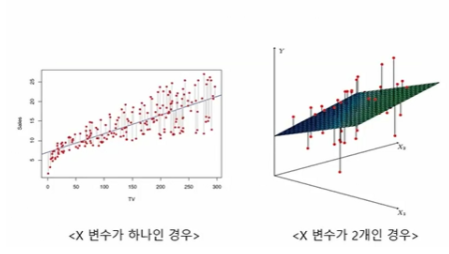
선형 회귀에서 발생하는 오차, 손실(Loss)
데이터들을 놓고 선을 긋는다는 건 결국 대~충 어림잡아본다는 뜻인데, 그러면 당연히 선은 실제 데이터와 약간의 차이가 발생한다. 일종의 오차라고 할 수 있는데, 앞으로는 손실(Loss)이라고 부르자.
아래 그림을 보면 A는 3, B는 1만큼의 손실이 발생했다.
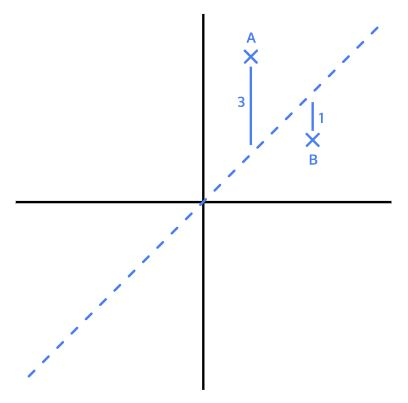
그런데 엄밀히 보면 + 혹은 - 방향을 고려하지 않고 얘기한거다. 선과 실제 데이터 사이에 얼마나 오차가 있는지 구하려면 양수, 음수 관계 없이 동일하게 반영되도록 모든 손실에 제곱을 해주는 것이 좋다.
그리고 이런 방식으로 손실을 구하는 걸 평균 제곱 오차(MSE)라고 부른다. 손실을 구할 때 가장 널리 쓰이는 방법이다.
손실을 구하는 이 외의 방법으로는 MSE처럼 제곱하지 않고 그냥 절대값으로 바로 평균을 구하는 평균 절대오차(MAE), MSE와 MAE를 절충한 후버손실(Huber Loss), 1-MSE/VAR로 구하는 결정계수(coefficient of determination) 등이 있다.
아무튼 결국 선형 회귀 모델의 목표는 모든 데이터로부터 나타나는 오차의 평균을 최소화할 수 있는 최적의 기울기와 절편을 찾는 것이다
손실을 최소화 하기 위한 방법, 경사하강법(Gradient Descent)
머신러닝에서 사용하는 모형은 (우리가 중고등학교 때 수학시간에 배운 단순한 방정식으로는 설명할 수 없을 만큼) 매우 복잡하기 때문에 선형 회귀 분석에서도 최적의 기울기와 절편을 구할 수 있는 마땅한 방법이 없다.
그런데 그나마 단서가 있다면 위에서 설명한 손실(Loss)을 함수로 나타내면 이렇게 아래로 볼록한 모양이라는 것이다.
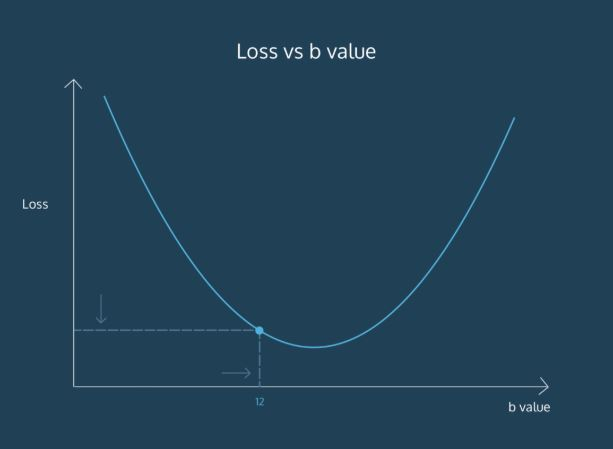
그래서 일단 파라미터를 임의로 정한 다음에 조금씩 변화시켜가며 손실을 점점 줄여가는 방법으로 최적의 파라미터를 찾아간다. (그리고 이때 미분이 사용되는데 당연히 직접할 필요 없으니 겁먹지 말자)
그리고 이런 방법을 경사하강법(Gradient Descent)이라 부른다.
예를 들어 절편을 구할 때 사용하는 공식은 다음과 같다.

이 값이 최소가 되도록 계속 b값을 변화시키는 거다.
그리고 기울기를 구하는 공식은 아래와 같다.
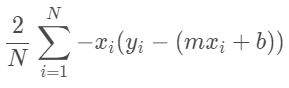
마찬가지로 이 값이 최소가 되도록 m값을 변화시키는 거다.
워워. 이 공식이 이해가 안되도 걱정하지 말자. 나도 깊이 들어가면 모른다. 지금은 일ㄹ단 개념만 이해하고 넘어가자.
수렴 (Convergence)
아무튼 선형 회귀 분석을 수행하면 기울기와 절편을 계속 변경해가면서 최적의 값을 찾게 될텐데, 이걸 언제까지 할지 정해줘야 한다. 무작정 계속 시킬수는 없으니까. 어차피 파라미터를 계속 조정하다보면 어느정도 최적의 값으로 수렴(converge)한다. 아래와 같은 모양으로.

위 그림을 보면 1000번 반복하니까 b값이 결국 약 47에 수렴하는 것을 알 수 있다. 그 이상 시도하는 건 별로 의미가 없어진다.
이걸 우리가 어떻게 결정할까? 어차피 머신러닝 알고리즘이 알아서 잘 수렴할거니 걱정 말자.
학습률 (Learning Rate)
다만 우리는 학습률(Learning Rate)이라는 걸 정해줄 필요가 있다.
아래 그림을 보면 학습률이 너무 커서 파라미터를 듬성듬성 조정한다.

이렇게 학습률을 크게 설정하면 최적의 값을 제대로 찾지 못한다. 일을 대충하는거다. 대신 일을 빨리 하긴 하겠지.
그렇다고 학습률을 작게 설정하면 최적의 값으로 수렴할 때까지 시간이 오래 걸린다.
그래서 모델을 학습시킬 때는 최적의 학습률을 찾는게 중요하다. 효율적으로 파라미터를 조정하면서도 결국 최적의 값을 찾아 수렴할 수 있을 수준으로.
결정계수의 개념 ()
(1) 회귀 없이 예측하기
만약 우리가 어떠한 샘플을 가지고 회귀가 무엇인지 모르는 상태에서 미래의 데이터를 예측해야하는 상황에 있다고 가정합시다.
그렇다면 어떤 방법이 가장 효율적인 방법일까요?
아마도 평균으로 예측하는 방법이 가장 오차가 적은 값으로 예측하는 방법일 것입니다.
여기서 오차를 측정하는 방법은 각 샘플에 대해서 잔차를 구하고 이를 제곱하면 하나의 면적이 됩니다. 모든 데이터에 대해서 이 면적의 합을 더하면 그것이 오차의 값이 될 것입니다.
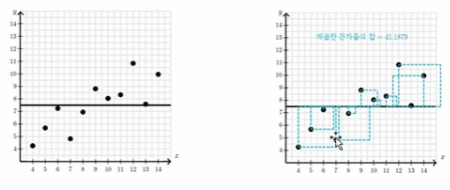
(2) 회귀로 예측하기
평균으로 예측한 오차의 값을 줄이기 위해서 우리는 회귀를 이용해 미래의 데이터를 예측할 수 있습니다.
회귀를 이용하면 오차의 제곱합이 최소가 되는 직선을 찾기 때문에 평균으로 예측한 상황보다 훨씬 오차가 줄어든 것을 확인할 수 있습니다.
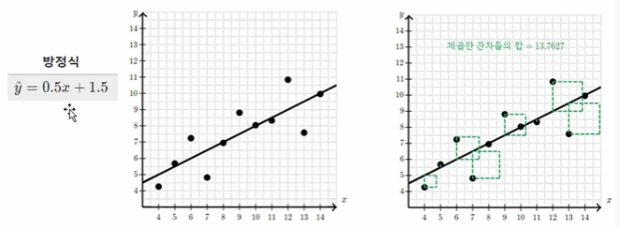
(3) 결정계수의 개념
이 때 회귀를 통해서 예측 오차가 줄어들었는지를 측정하는 방법으로 결정계수를 구할 수 있습니다.
- 회귀를 사용하지 않았을 때 제곱한 잔차의 합 : 41.1879
- 회귀를 사용했을 때 제곱한 잔차의 합 : 13.7627
- 줄어든 제곱한 잔차의 합 : 41.1879 - 13.7627 = 27.4252
이를 백분율로 나타내면 66.57%입니다.
66.59%라는 값이 결정계수()이며 결정계수는 Y의 변동 비율과 회귀모델의 설명력을 나타냅니다.

고전적 선형 회귀 모델은 형태가 단순한만큼 데이터에 대해 많은 가정을 가지고 있다.
- 오차항은 평균이 0이고 분산이 일정한 정규분포를 갖는다
- 독립변수와 종속변수는 선형 관계이다.
- 오차항은 자기 상관성이 없다.
- 데이터에 아웃라이어가 없다
- 독립변수와 오차항은 서로 독립이다.
- 독립변수 간에서는 서로 선형적으로 독립이다.
따라서 만약 실제 데이터가 이런 가정을 충적하지 않는다면, 고전적 선형회귀 모델은 실제 데이터를 정확히 반영하지 못하게 되므로 다른 방법을 사용해야 합니다. 일반적으로 알려진 가이드라인은 다음과 같습니다.
- 독립변수와 종속변수가 선형 관계가 아닌경우 : Polynomial regression, Generalized Additive Model (GAM)
- 오차항의 확률분포가 정규분포가 아닌 경우 : Generalized Linear Model (GLM)
- 오차항에 자기 상관성이 있는 경우 : Auto-regression
- 데이터에 아웃라이어가 있는 경우 : Robust regression, Quantile regression
- 독립변수 간에 상관성이 있는 경우 (다중공선성) : Ridge regression, Lasso regression, Elastic Net regression, Principal Component Regression (PCR), Partial Least Square (PLS) regression
출처
https://kimdingko-world.tistory.com/101
https://hleecaster.com/ml-linear-regression-concept/
