.png)
1. K-평균 (K-Means)
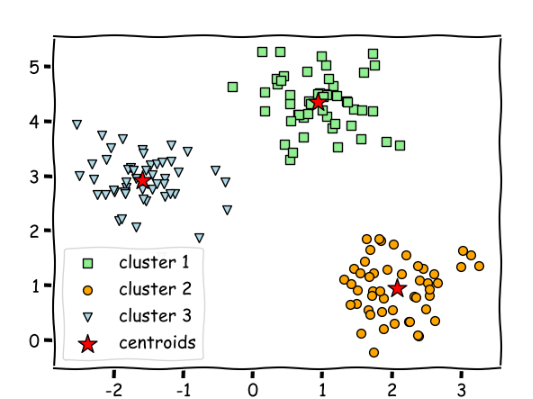
군집 중심점(centroid)이라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법
선택된 포인트의 평균지점으로 이동하고 이동된 중심점에서 다시 가까운 포인트를 선택, 다시 중심점을 평균 지점으로 이동하는 프로세스를 반복적으로 수행
장점
- 일반적으로 군집화에서 가장 많이 사용되는 알고리즘
- 알고리즘이 쉽고 간결하다
단점
- 거리기반 알고리즘으로 속성의 개수가 매우 많을수록 군집화 정확도가 떨어짐 (PCA 차원감소 적용)
- 반복을 수행하는데 반복횟수가 많을 경우 매우 느려짐
- 몇 개의 군집을 선택해야할 지 가이드하기가 어려움
2. 평균 이동 (Mean Shift)
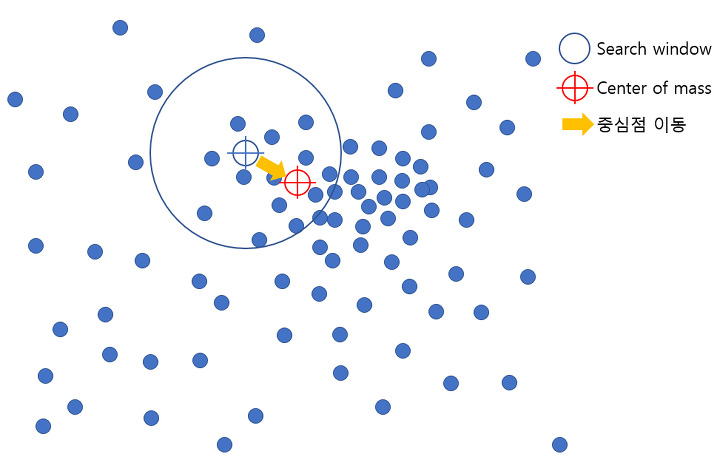
K 평균과 유사하지만 거리 중심이 아니라 데이터가 모여있는 밀도가 가장 높은 곳으로 군집 중심점을 이동하면서 군집화를 수행함
일반 업무 기반의 정형 데이터 세트보다 컴퓨터 비전 영역에서 이미지나 영상 데이터에서 특정 개체를 구분하거나 움직임을 추적하는데 뛰어난 역할을 수행하는 알고리즘이다.
이러한 특성 때문에 업무 기반의 데이터 세트보다는 컴퓨터 비전 영역에서 잘 사용된다.
장점
-
데이터 세트의 형태를 특정 형태로 가정한다든가, 특정 분포도 기반의 모델로 가정하지 않기 때문에 좀 더 유연한 군집화 가능
-
이상치의 영향력이 크지 않다
-
미리 군집의 개수를 정할 필요가 없다
단점
- 알고리즘 수행시간이 오래 걸린다
- bandwidth의 크기에 따른 군집화 영향도가 매우 크다
3. GMM(Gaussian Mixture Model)
군집화를 적용하는 데이터가 여러개의 가우시안 분포 모델을 섞어서 생성된 모델로 가정해 수행하는 방식
Q. 가우시안(Gaussian) 분포란?
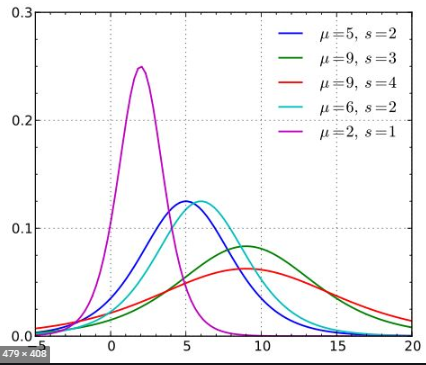
A. 좌우 대칭형의 bell 형태를 가진 통계학에서 가장 잘 알려진 연속확률 함수
-
GMM은 데이터를 여러개의 가우시안 분포가 섞인것으로 간주 ---> 섞인 데이터 분포에서 개별 유형의 가우시안 분포를 추출한다.
-
전체 데이터 세트는 서로 다른 정규분포를 가진 여러가지 확률 분포 곡선으로 구성되어 있으며, 정규분포에 기반에 군집화를 수행하는 것이 GMM 군집화 방식
-
일정한 데이터 세트가 있으면 이를 구성하는 여러개의 정규 분포 곡선 추출 뒤, 개별 데이터가 이 중 어떤 정규분포에 속하는지 결정
-
이러한 방식을 모수추정이라고 하며 "개별 정규 분포의 평균과 분산", "각 데이터가 어떤 정규 분포에 해당되는지의 확률"을 구하기 위해서 추정한다
-
GMM은 모수추정을 하기 위해 EM(Expectation and Maximization)방법을 적용하고 있다.
4. DBSCAN
-
DBSCAN(Density Based Spatial Clustering of Applications with Noise)
밀도 기반 군집화의 대표적 예 -
간단하고 직관적인 알고리즘으로 되어 있음에도 데이터의 분포가 기하학적으로 복잡한 데이터 세트에도 효과적인 군집화가 가능
-
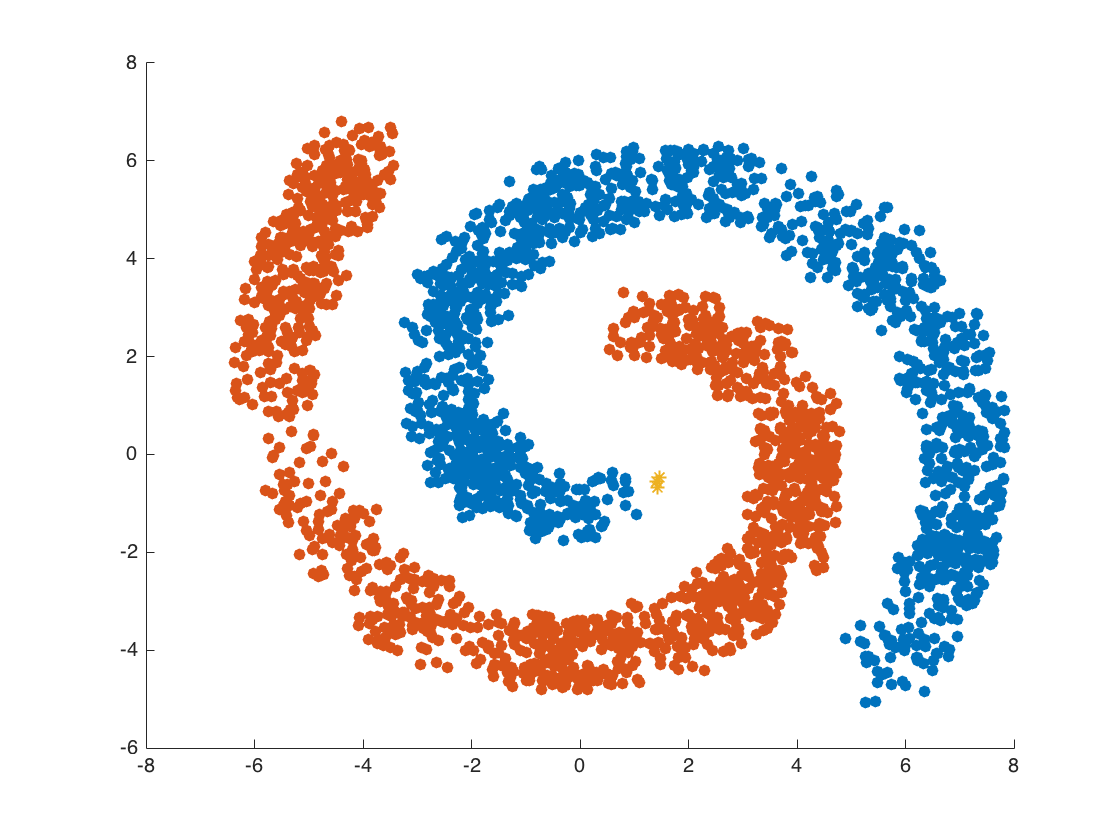
특정 공간 내에 데이터 밀도 차이를 기반 알고리즘으로 하고 있어서 복잡한 기하학적 분포도를 가진 데이터 세트에 대해서도 군집화를 잘 수행한다.
-
아래의 복잡한 군집화도 가능!
출처
http://www.tcpschool.com
https://bangu4.tistory.com/96?category=904392
https://bangu4.tistory.com/98?category=904392
