서포트 벡터 머신(Support Vector Macine, SVM)

오혜수·2022년 3월 11일

머신러닝

목록 보기

20/33

서포트 벡터 머신(SVM: Support Vector Machine)은 분류와 회귀 과제에 사용할 수 있는 강력한 머신러닝 지도학습 모델이다. 일단 이 SVM의 개념만 최대한 쉽게 설명해본다. 중간중간 파이썬 라이브러리 scikit-learn을 사용한 아주 기초적인 실습을 통해 개념 이해를 돕는다.

목차는 아래와 같다.

서포트 벡터 머신이란
최적의 결정 경계 (Decision Boundary)
마진(Margin)
이상치(Outlier)를 얼마나 허용할 것인가
커널(Kernel)
- 다항식(Polynomial)
- 방사 기저 함수(RBF: Radial Bias Function)
요약

내용이 많지 않으니 후딱 살펴보자.

1. 서포트 벡터 머신이란

서포트 벡터 머신(이하 SVM)은 결정 경계(Decision Boundary), 즉 분류를 위한 기준 선을 정의하는 모델이다. 그래서 분류되지 않은 새로운 점이 나타나면 어느 쪽에 속하는지 확인해서 분류 과제를 수행할 수 있게 된다.

결국 이 결정 경계라는 걸 어떻게 정의하고 계산하는지 이해하는게 더 중요하다는 뜻이다.

일단 예시를 보자.

만약 데이터에 2개 속성(feature)만 있다면 결정 경계는 이렇게 간단한 선 형태가 될 거다.

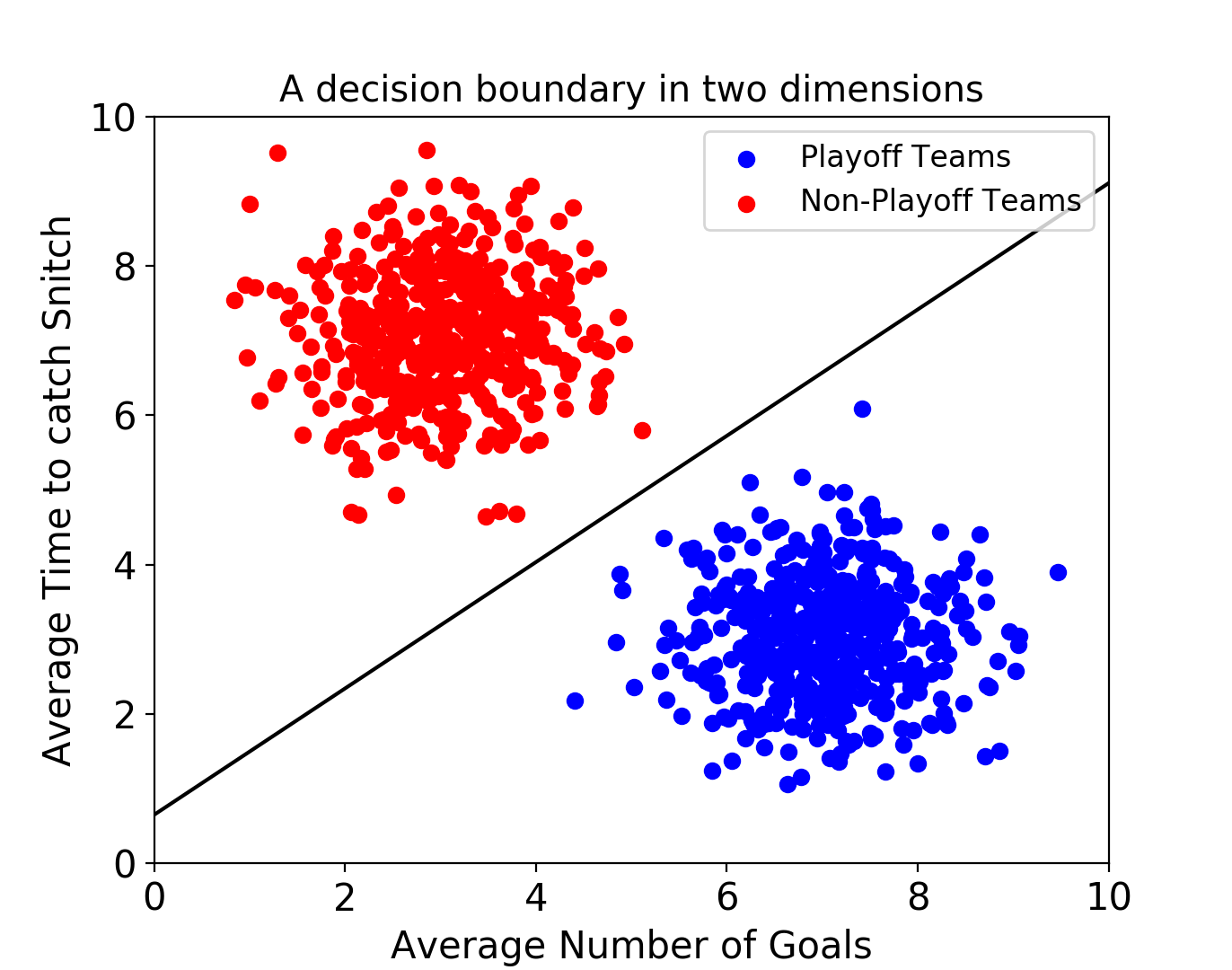
그러나 속성이 3개로 늘어난다면 이렇게 3차원으로 그려야 한다.

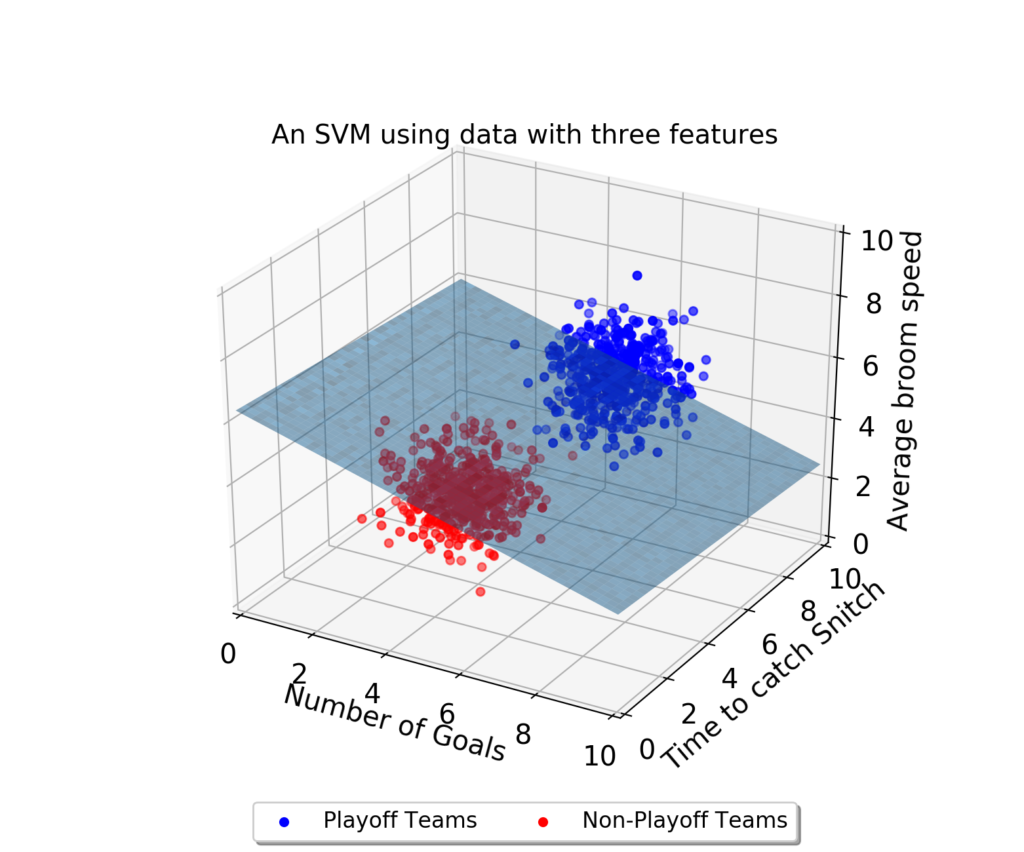
그리고 이 때의 결정 경계는 '선'이 아닌 '평면'이 된다.

우리가 이렇게 시각적으로 인지할 수 있는 범위는 딱 3차원까지다. 차원, 즉 속성의 개수가 늘어날수록 당연히 복잡해질 거다. 결정 경계도 단순한 평면이 아닌 고차원이 될 텐데 이를 "초평면(hyperplane)"이라고 부른다. (어렵게 생각할 필요는 없다. 일단 용어만 알고 넘어가자.)

2. 최적의 결정 경계(Decision Boundary)

결정 경계는 무수히 많이 그을 수 있을 거다. 어떤 경계가 좋은 경계일까?

일단 아래 그림들을 보자.

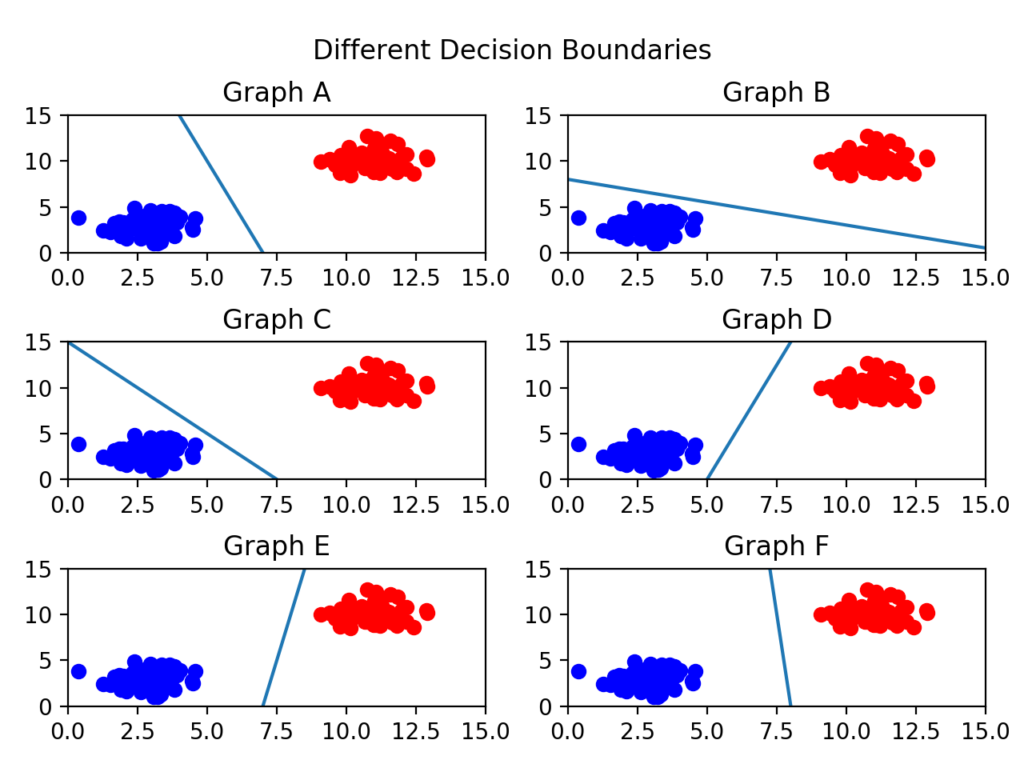
어떤 그래프가 제일 위태로워 보이는가?
C를 보면 선이 파란색 부류와 너무 가까워서 아슬아슬해보인다.

그렇다면 어떤 결정 경계가 가장 적절해보이는가?
당연히 F다. 두 클래스(분류) 사이에서 거리가 가장 멀기 때문이다.

이런 결정 경계는 데이터 군으로부터 최대한 멀리 떨어지는 게 좋다는 걸 알았다. 실제로 서포트 벡터 머신(Support Vector Machine)이라는 이름에서 Support Vectors는 결정 경계와 가까이 있는 데이터 포인트들을 의미한다. 이 데이터들이 경계를 정의하는 결정적인 역할을 하는 셈이다.

이어서 마진(Margin)이라는 용어에 대해 알아보자.

3. 마진(Margin)

마진(Margin)은 결정 경계와 서포트 벡터 사이의 거리를 의미한다.

아래 그림을 보면 바로 이해된다.

가운데 실선이 하나 그어져있는데, 이게 바로 '결정 경계'가 되겠다. 그리고 그 실선으로부터 검은 테두리가 있는 빨간점 1개, 파란점 2개까지 영역을 두고 점선을 그어놓았다. 점선으로부터 결정 경계까지의 거리가 바로 '마진(Margin)'이다.

여기서 일단 결론을 하나 얻을 수 있다. 최적의 결정 경계는 마진을 최대화한다.

그리고 위 그림에서는 x축과 y축 2개의 속성을 가진 데이터로 결정 경계를 그었는데, 총 3개의 데이터 포인트(서포트 벡터)가 필요했다. 즉, n개의 속성을 가진 데이터에는 최소 n+1개의 서포트 벡터가 존재한다는 걸 알 수 있다.

이번엔 SVM 알고리즘의 장점을 하나 알 수 있다.

대부분 머신러닝 지도 학습 알고리즘은 학습 데이터 모두를 사용하여 모델을 학습한다. 그런데 SVM에서는 결정 경계를 정의하는 게 결국 서포트 벡터이기 때문에 데이터 포인트 중에서 서포트 벡터만 잘 골라내면 나머지 쓸 데 없는 수많은 데이터 포인트들을 무시할 수 있다. 그래서 매우 빠르다.

scikit-learn 사용법

SVM에서 결정 경계를 구하는 건 상당히 복잡한 최적화 문제다. 이 계산 과정을 온전히 이해하는 건 나 같은 무지렁이에겐 너무 버거운 일일 거다.

그러나 파이썬 scikit-learn 라이브러리가 있으니 일단 이걸 통해 SVM을 구현해보자. 게다가 scikit-learn을 활용하면 모델을 구현할 때 사용되는 추가적인 개념도 익힐 수 있다.

① Classification : SVC

SVM은 회귀와 분류 모두 사용 가능하다.
이름에서 유추할 수 있다시피, SVC는 SVM에서 M을 C(Classification)으로 바꾼 것이다. 회귀는 SVR(Regression)이다.

일단 아래 그림과 같이 선을 긋는 연습을 해보자.

일단 SVC를 불러올 때 kernel = 'linear'라고 지정해줬다. 이건 뒤에서 설명할 예정이니 일단 넘어가고..!

레이블은 빨간걸 1, 파란걸 0으로 보면 된다.

그리고 .fit() 안에 학습 데이터와 레이블을 넣어주면 짠!하고 선을 긋는 거다. 이게 끝이다.

이제 .predict() 메서드를 통해 분류를 해볼 수 있다. 예를 들어 [3,2]라는 데이터를 넣어 예측을 하려면 이렇게

위 그림에서 직접 눈으로 [3,2] 좌표를 찍어봐도 알 수 있듯 빨간 점은 1로 분류될 거다.

그리고 위에서 설명한 서포트 벡터, 결정 경계를 정의하는 서포트 벡터를 확인하려면 classifier.support_vectors_를 point해보면 된다.

이렇게 나올거다.

파란 점 2개와 빨간 점 1개를 사용했다.

② Regression : SVR

이제, SVM 을 회귀에 적용시켜보자.

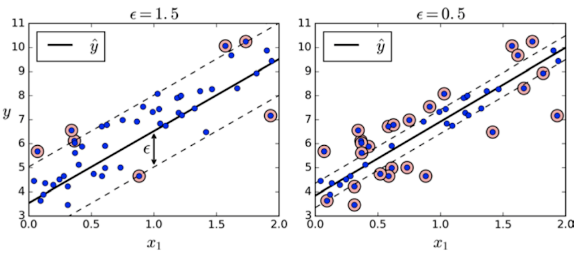
SVM 을 회귀에 적용하는 방법은, SVC 와 목표를 반대로 하는 것이다.

즉, 마진 내부에 데이터가 최대한 많이 들어가도록 학습하는 것이다.
마진의 폭은 epilson 이라는 하이퍼파라미터를 사용하여 조절한다.

  import numpy as np
  from sklearn import datasets
  from sklearn.svm import SVR
  from sklearn.metrics import mean_squared_error, explained_variance_score
  from sklearn.utils import shuffle

  data = datasets.load_boston()

  X, y = shuffle(data.data, data.target, random_state = 7)

  num_training = int(0.8 * len(X))
  X_train, y_train = X[:num_training], y[:num_training]
  X_test, y_test = X[num_training:], y[num_training:]

  # Create Support Vector Regression model
  # kernel : 선형 커널
  # C : 학습 오류에 대한 패널티, C 값이 클 수록 모델이 학습 데이터에 좀 더 최적화 됨, 너무 크면 오버피팅 발생
  # Epsilon : 임계값, 예측한 값이 GT 범위 안에 있으면 패널티 부여 X
  
  sv_regressor = SVR(kernel='linear', C=1.0, epsilon=0.1)

  sv_regressor.fit(X_train, y_train)

  y_pred = sv_regressor.predict(X_test)

  mse = mean_squared_error(y_test, y_pred)
  evs = explained_variance_score(y_test, y_pred)

  test_data = [3.7, 0, 18.4, 1, 0.87, 5.95, 91, 2.5052, 26, 666, 20.2, 351.34, 15.27]
  print(sv_regressor.predict([test_data])[0])

4. 이상치(Outlier)를 얼마나 허용할 것인가

SVM은 데이터 포인트들을 올바르게 분리하면서 마진의 크기를 최대화해야 하는데, 결국 이상치(outlier)를 잘 다루는 게 중요하다.

아래 그림을 보자. 선을 살펴보기에 앞서 왼쪽에 혼자 튀어 있는 파란 점과, 오른쪽에 혼자 튀어 있는 빨간 점이 있다는 걸 봐두자. 누가 봐도 아웃라이어다.

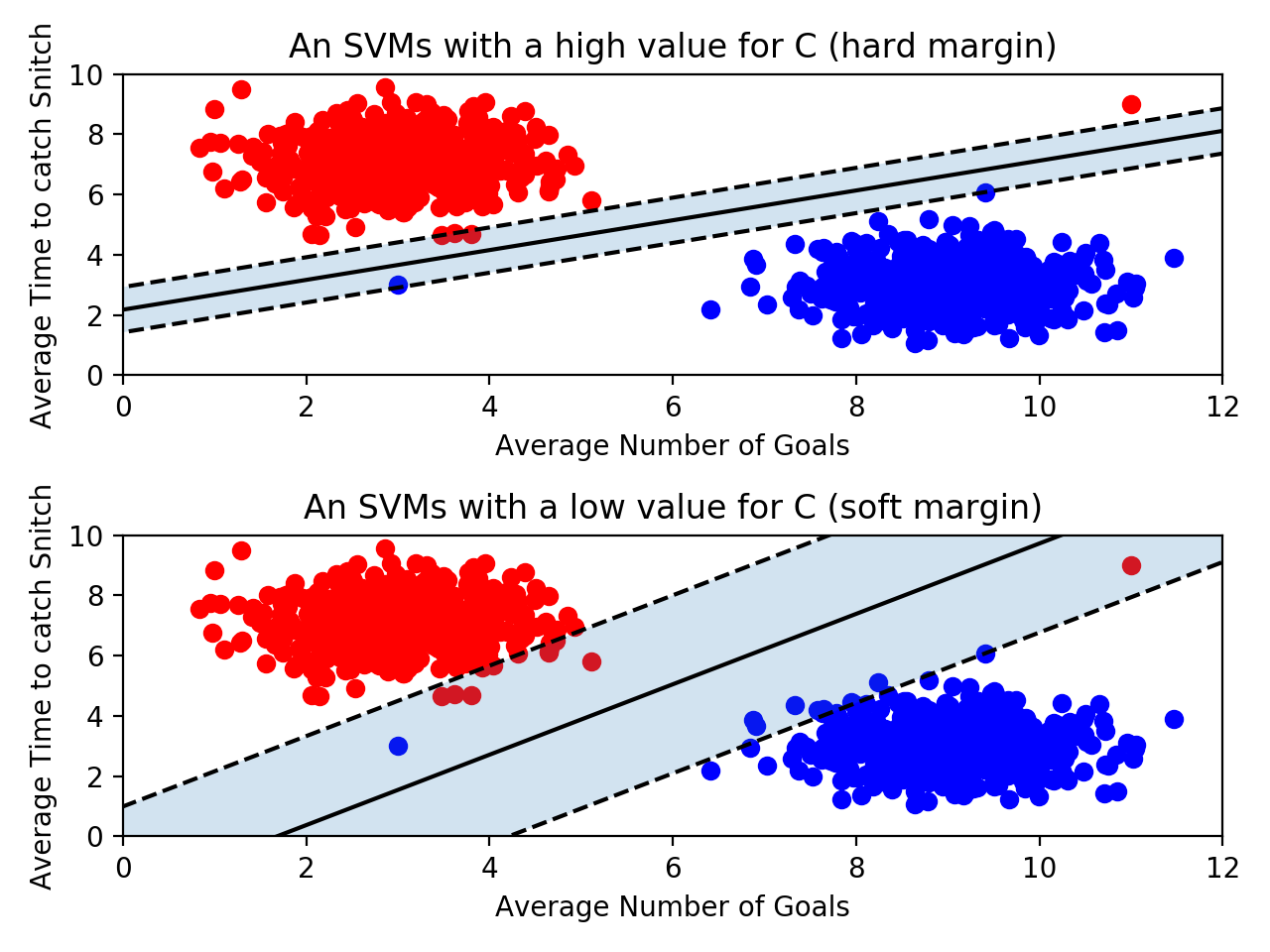
이제 위 아래 그림을 좀 더 자세히 비교해보자.

위의 그림은 아웃라이어를 허용하지 않고 기준을 까다롭게 세운 모양이다. 이걸 하드 마진(hard margin)이라고 부른다. 그리고 서포트 벡터와 결정 경계 사이의 거리가 매우 좁다. 즉, 마진이 매우 작아진다. 이렇게 개별적인 학습 데이터들을 다 놓치지 않으려고 아웃라이어를 허용하지 않는 기준으로 결정 경계를 정해버리면 오버피팅(overfitting) 문제가 발생할 수 있다.
아래 그림은 아웃라이어들이 마진 안에 어느정도 포함되도록 너그럽게 기준을 잡았다. 이걸 소프트 마진(soft margin)이라고 부른다. 이렇게 너그럽게 잡아 놓으니 서포트 벡터와 결정 경계 사이의 거리가 멀어졌다. 즉, 마진이 커진다. 대신 너무 대충대충 학습하는 꼴이라 언더피팅(underfitting) 문제가 발생할 수 있다.

오버피팅과 언더피팅에 대한 개념은 머신러닝에서 무조건 알아야 하는 개념이다. 이 포스팅을 참고하자.

파라미터 C

그리고 scikit-learn에서는 SVM 모델이 오류를 어느정도 허용할 것인지 파라미터 C를 통해 지정할 수 있다. (기본값은 1이다.)

C값이 클수록 하드마진(오류 허용 안함), 작을수록 소프트마진(오류를 허용함)이다.

당연히 C의 최적값은 데이터에 따라 다르다. 결국 여러가지 C값을 넣어보면서 모델을 검증하는 수밖에 없다.

5. 커널(Kernel)

지금까지는 선형으로 결정 경계를 그을 수 있는 형태의 데이터 세트를 예시로 들었다. 그런데 만약 SVM이 선형으로 분리할 수 없는 세트가 있다면 어떻게 해야 할까?

극단적인 예로 들어 이런 데이터가 있다고 해보자.

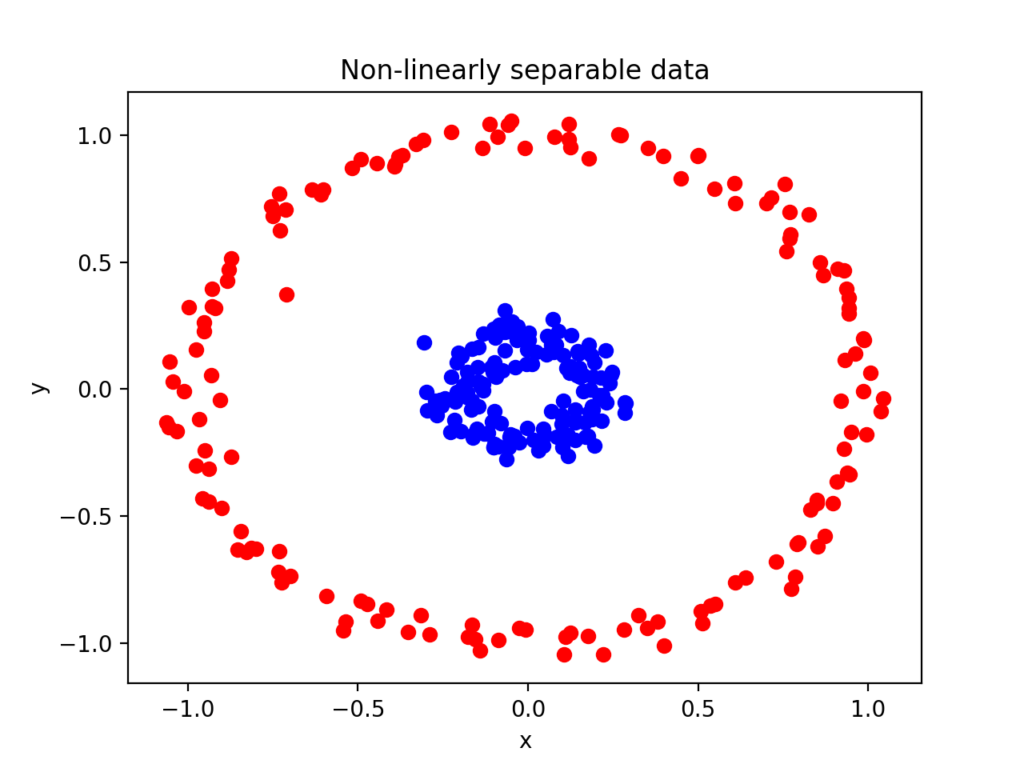
빨간색 점을 파란색 점과 분리하는 직선을 그릴 수가 없다.

그러나 다행히도 scikit-learn에서는 SVM 모델을 만들 때 kernel을 지정하여 해결할 수 있다.

보통은 이렇게 선형(linear)으로 지정하지만

poly 같은 걸 넣어줄 수도 있다. 이어서 좀 더 알아보겠다. 다만, 다른 커널을 사용할 때는 주의가 필요하다. 머신러닝 모델이 약간의 오차를 허용해야 하는 건 너무나 당연한 거라 단순히 outlier 때문에 선형으로 분리할 수 없다고 판단해서는 안 된다. 일부 아웃라이어에 맞추기 위해 비선형으로 결정 경계를 만들 필요가 없다는 뜻이다. 모든 점을 올바르게 분리하는 선을 그린다는 건 결국 모델이 데이터에 과도하게 적합해지는, 즉 오버피팅 된다는 거니까.

다른 커널들에 대해서도 좀 알아보자.

1. 다항식 (Polynomial)

위에서 봤던 이 그림을 다시 보면

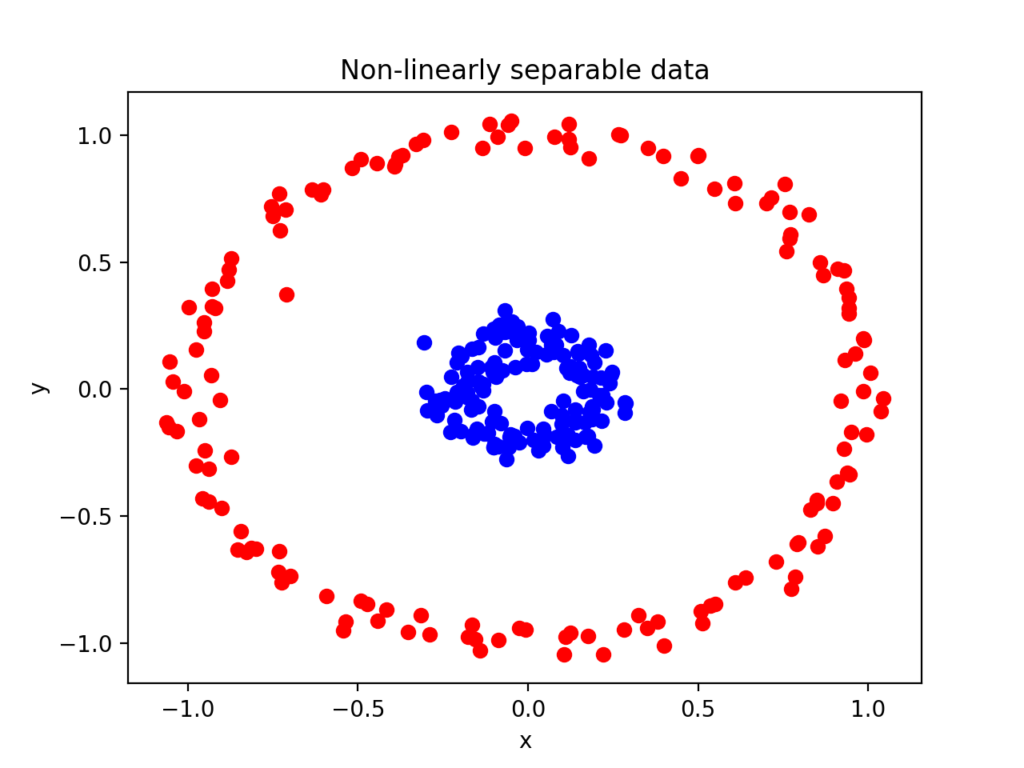
아무리 봐도 단순한 선형으로는 도저히 해결이 안된다.

이때 다항식(polynomial) 커널을 사용하면 2차원에서 x,y 좌표로 이루어진 점들을 아래와 같은 식에 따라 3차원으로 표현하게 된다.

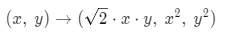
예를 들어 [1,2] 점이 있다고 하면 이렇게 3차원으로 계산해놓는다.

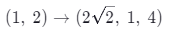
그리고 이렇게 다항식 커널로 계산한 데이터 포인트들을 3차원으로 그려보면 이런 모양이 나타난다.

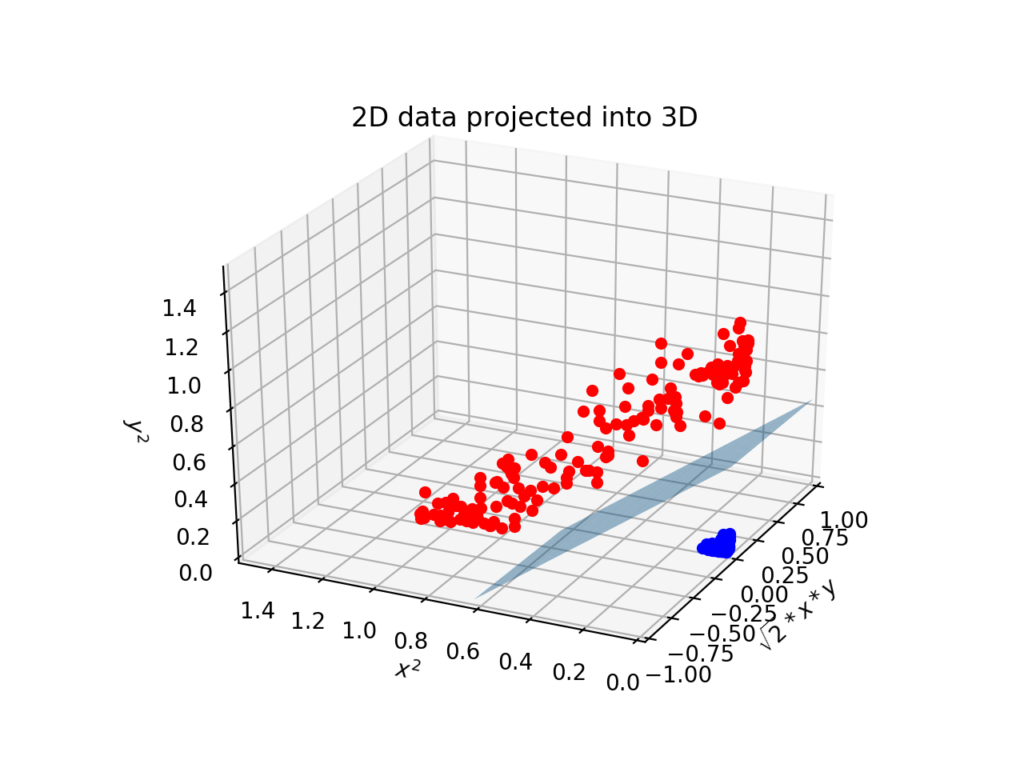
오.. 드디어 뭔가 결정 경계를 그어볼 수 있는 꼴로 바뀐 걸 알 수 있다.

이렇게 다항식(polynomial) 커널을 사용하면 데이터를 더 높은 차원으로 변형하여 나타냄으로써 초평면(hyperplane)의 결정 경계를 얻을 수 있다.

2. 방사 기저 함수 (RBF : Radial Bias Function)

이건 이름이 좀 어려운데, 보통 RBF 커널 혹은 가우시안 커널이라고 부르기도 한다.

scikit-learn에서 모델을 불러올 때 파라미터로 kernel 값을 따로 안 넣어주었을 때의 기본값이 바로 이 rbf다. (위에서 언급했던 linear, poly, 그리고 sigmoid와 같은 걸로 지정해줄 수도 있다)

위에서 살펴본 'poly' (다항식) 커널은 2차원의 점을 3차원으로 변환했다.

그런데 이 RBF 커널은 2차원의 점을 무한한 차원의 점으로 변환한다. 그래서 시각화 하는 건 어렵고.. 커널이 이 작업을 수행하는 방법에 대해서도 이해하기 어려우니 다루지 않을 거다. 상당히 복잡한 선형대수학이 사용된다는 것만 알고 넘어가자.

그러나 하나 알고 가야 할 게 있다. 바로 감마(gamma)다.

6. 파라미터 gamma

gamma는 (위에서 소개한 C와 마찬가지로) 파라미터다.

gamma는 결정 경계를 얼마나 유연하게 그을 것인지 정해주는 거다. 학습 데이터에 얼마나 민감하게 반응할 것인지 모델을 조정하는 거니까 C와 비슷한 개념이라고 봐도 된다.

gamma 값을 높이면 학습 데이터에 많이 의존해서 결정 경계를 구불구불 긋게 된다. 이는 오버피팅을 초래할 수 있다.
반대로 gamma를 낮추면 학습 데이터에 별로 의존하지 않고, 결정 경계를 직선에 가깝게 긋게 된다. 이러면 언더피팅이 발생할 수 있다.

그림으로 보면 이해가 쉬우니 살펴보자.

일단 gamma가 적당하면 이런 모양이다.

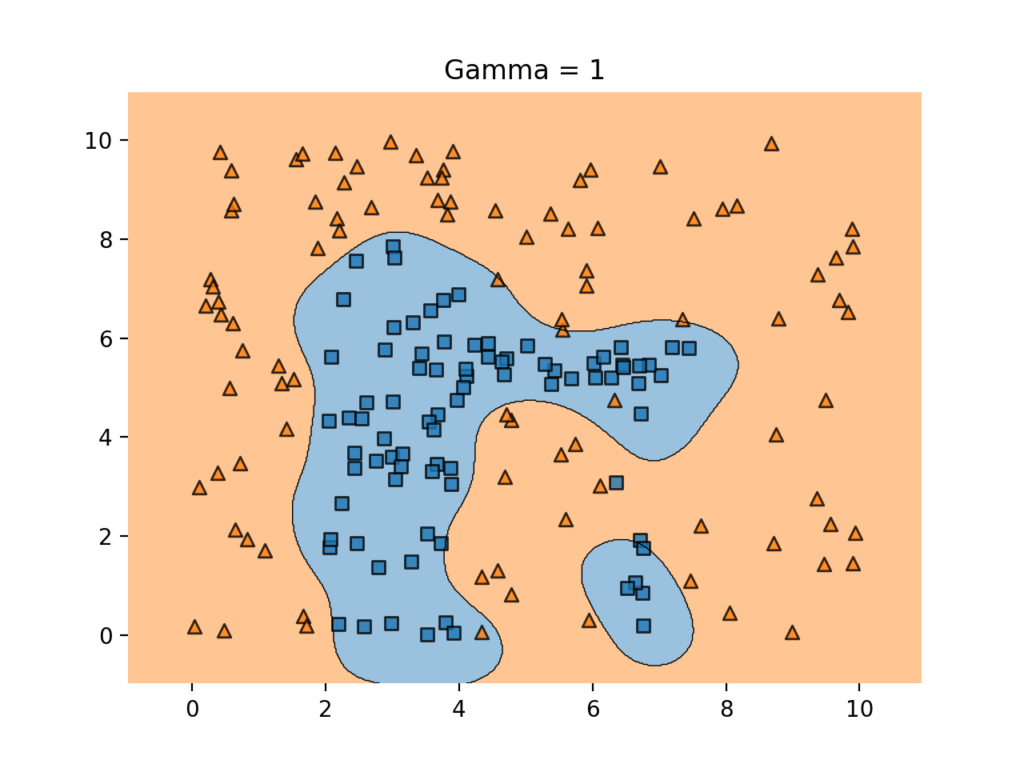
그러나 만약 gamma를 너무 높이면 이런 꼴이 되어 오버피팅이 발생한다.

반대로 gamma를 너무 낮게 잡으면 이렇게 결정 경계를 너무 대충 그려서 언더피팅이 발생한다.

요약

여기까지 이해하면 SVM, 서포트 벡터 머신 알고리즘에 대해 어느정도 감은 잡은 셈이다.

위에서 다룬 내용을 가볍게 요약하면 아래와 같다.

SVM은 분류에서 많이 사용하지만 회귀에서도 사용되는 지도학습 머신러닝 모델이다.
SVM은 서포트 벡터(support vector)를 사용해서 결정 경계(Decision Boundary)를 정의하고, 분류되지 않은 점을 해당 결정 경계와 비교해서 분류한다.
**서포트 벡터(support vectors)는 결정 경계에 가장 가까운 각 클래스의 점들이다.
서포트 벡터 결정 경계 사이의 거리를 마진(margin)이라고 한다.
SVM은 허용 가능한 오류 범위 내에서 가능한 최대 마진을 만들려고 한다.
파라미터 C는 허용되는 오류 양을 조절한다. C 값이 클수록 오류를 덜 허용하며 이를 하드마진(hard margin)이라 부른다. 반대로 C값이 작을수록 오류를 더 많이 허용해서 소프트 마진(soft margin)을 만든다.
SVM에서는 선형으로 분리할 수 없는 점들을 분류하기 위해 커널(kernel)을 사용한다.
커널(kernel)은 원래 가지고 있는 데이터를 더 높은 차원의 데이터로 변환한다. 2차원의 점으로 나타낼 수 있는 데이터를 다항식(polynomial) 커널은 3차원으로, RBF 커널은 무한한 차원으로 변환한다.
RBF 커널에는 파라미터 감마(gamma)가 있다. 감마가 너무 크면 학습 데이터에 너무 의존해서 오버피팅이 발생할 수 있다.