깊이우선탐색 DFS (JAVA)

횽·2024년 8월 2일

algorithm&data-structure

목록 보기

6/18

📍 DFS란?

: Depth-First Search(깊이우선탐색)으로,
루트 노드(혹은 다른 임의의 노드)에서 시작해서 가능한 한 깊게 탐색한 후 더 이상 탐색할 수 없을 경우 이전 노드로 되돌아가서 다음 경로를 탐색한다.
-> 모든 노드를 탐색할 때 사용한다.

1. BFS vs DFS

(1) 깊이 우선 탐색 DFS

노드 간의 "하나 하나" 모든 관계를 알아야 할 때 사용한다.
재귀적인 특성을 가진다. -> 재귀함수 사용
후입선출(LIFO) 원칙으로 탐색 -> 스택 사용

(2) 너비 우선 탐색 BFS

노드의 최단 경로를 찾을 때 사용한다.
깊이 관련 특성을 가진다.
재귀적인 특성을 가지고 있지 않다.
선입선출(FIFO) 원칙으로 탐색 -> 큐 사용

2. DFS 해결 방식

스택 또는 재귀를 이용하여 해결한다.

(1) 스택
스택에 가장 깊은 노드까지 삽입한다.
스택 pop한 후 그 노드에 연결된 가장 깊은 노드까지 삽입한다.
스택이 empty할 때까지 위의 과정을 반복한다.

(2) 재귀

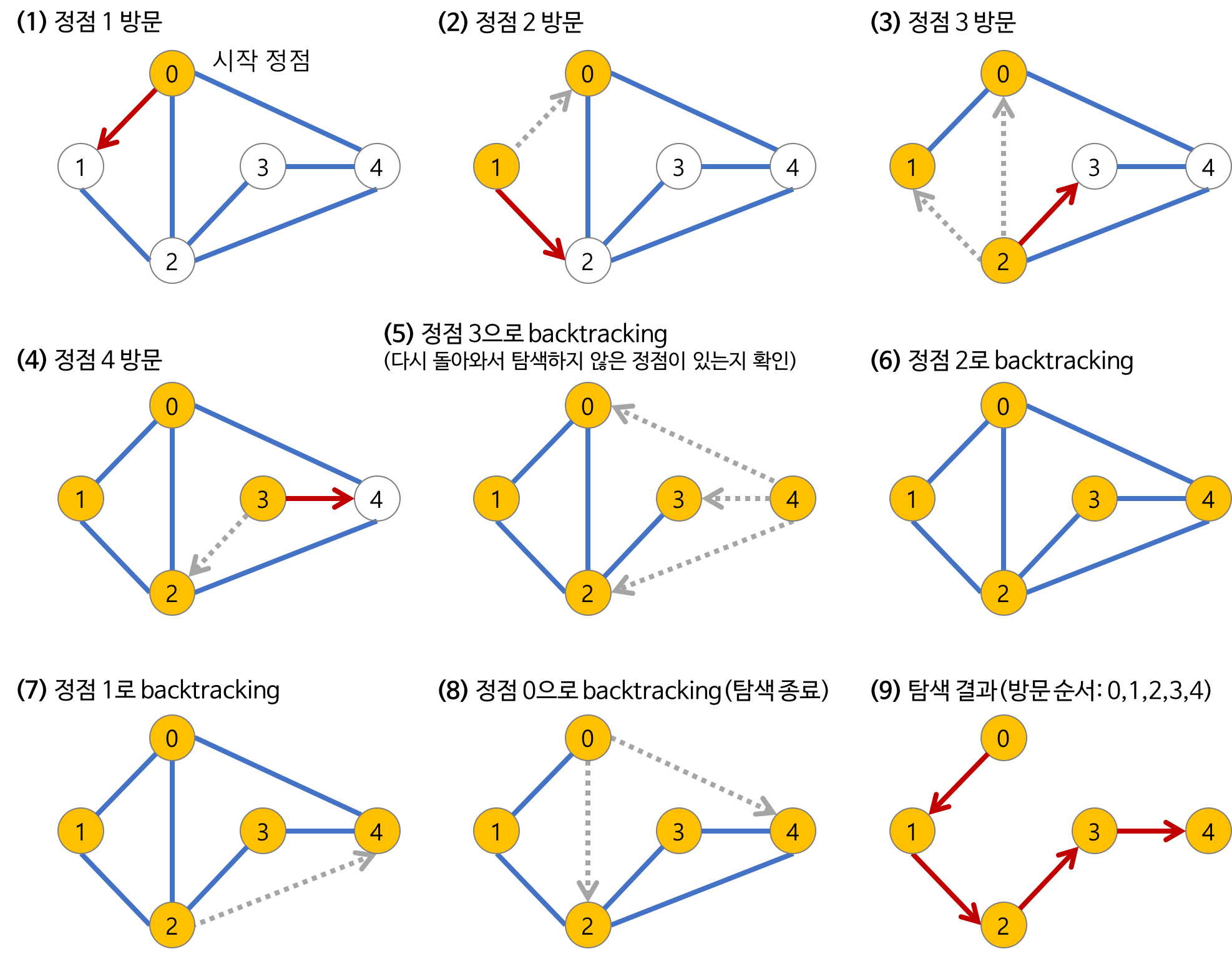
출처 : https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html

3. 시간복잡도

DFS의 시간 복잡도 : O(V + E)

노드 수(V): 그래프에 있는 노드(정점)의 수
간선 수(E): 그래프에 있는 간선(엣지)의 수

4. 구현 (JAVA)

(1) 재귀를 이용한 DFS 구현

자바 코드

import java.util.*;

public class DFSExample {
    static List<List<Integer>> graph = new ArrayList<>();
    static boolean[] visited;

    public static void main(String[] args) {
        int n = 6; // 노드 개수 (0부터 5까지)
        visited = new boolean[n];

        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }

		// 그래프 간선 추가 (무방향 그래프)
        graph.get(0).addAll(Arrays.asList(1, 2));
        graph.get(1).addAll(Arrays.asList(0, 3, 4));
        graph.get(2).addAll(Arrays.asList(0, 5));
        graph.get(3).add(1);
        graph.get(4).add(1);
        graph.get(5).add(2);

        System.out.println("DFS 탐색 순서:");
        DFS(0); // 0번 노드에서 시작
    }
    
     public static void DFS(int node) {
        visited[node] = true;
        System.out.print(node + " ");

        for (int neighbor : graph.get(node)) {
            if (!visited[neighbor]) {
                DFS(neighbor);
            }
        }
    }
}

출력

DFS 탐색 순서:
0 1 3 4 2 5

그래프 구조

탐색 과정

DFS(0) 호출
0 방문 → visited[0] = true
0의 이웃 1 → 방문 안 했으므로 DFS(1) 호출

DFS(1) 호출
1 방문 → visited[1] = true
1의 이웃 0 → 이미 방문했으므로 무시
1의 이웃 3 → 방문 안 했으므로 DFS(3) 호출

DFS(3) 호출
3 방문 → visited[3] = true
3의 이웃 1 → 이미 방문했으므로 무시
더 탐색할 노드 없음 → DFS(3) 종료, DFS(1)으로 복귀
DFS(1)으로 복귀
1의 이웃 4 → 방문 안 했으므로 DFS(4) 호출

DFS(4) 호출
4 방문 → visited[4] = true
4의 이웃 1 → 이미 방문했으므로 무시
더 탐색할 노드 없음 → DFS(4) 종료, DFS(1)으로 복귀
DFS(1) 종료 후 DFS(0)으로 복귀
0의 이웃 2 → 방문 안 했으므로 DFS(2) 호출

DFS(2) 호출
2 방문 → visited[2] = true
2의 이웃 0 → 이미 방문했으므로 무시
2의 이웃 5 → 방문 안 했으므로 DFS(5) 호출

DFS(5) 호출
5 방문 → visited[5] = true
5의 이웃 2 → 이미 방문했으므로 무시
더 탐색할 노드 없음 → DFS(5) 종료, DFS(2)로 복귀
DFS(2) 종료 후 DFS(0)으로 복귀
모든 노드를 탐색 완료 → DFS(0) 종료

(2) 스택을 이용한 DFS 구현

자바 코드

import java.util.*;

public class DFSStackExample {
    static List<List<Integer>> graph = new ArrayList<>();
    static boolean[] visited;

    public static void main(String[] args) {
        int n = 6;
        visited = new boolean[n];

        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }
		// 그래프 간선 추가 (무방향 그래프)
        graph.get(0).addAll(Arrays.asList(1, 2));
        graph.get(1).addAll(Arrays.asList(0, 3, 4));
        graph.get(2).addAll(Arrays.asList(0, 5));
        graph.get(3).add(1);
        graph.get(4).add(1);
        graph.get(5).add(2);

        System.out.println("DFS 탐색 순서:");
        DFS(0);
    }
    
    private static void DFS(int start) {
        Stack<Integer> stack = new Stack<>();
        stack.push(start);

        while (!stack.isEmpty()) {
            int node = stack.pop(); // 스택에서 node 꺼내기
			
            if (!visited[node]) {
                visited[node] = true;
                System.out.print(node + " ");
				
                // 스택에서는 마지막에 삽입된 node가 먼저 탐색된다.
                // 스택은 후입선출이기 때문이다.
                for (int i = graph.get(node).size() - 1; i >= 0; i--) {
                    int neighbor = graph.get(node).get(i);
                    if (!visited[neighbor]) {
                        stack.push(neighbor);
                    }
                }
            }
        }
    }
}

탐색 과정

시작 노드 0을 스택에 넣고 방문 표시
스택에서 0을 꺼내 출력하고, 이웃 노드 (1, 2)를 역순(2 → 1) 으로 스택에 추가
스택에서 1을 꺼내 출력하고, 이웃 노드 (3, 4)를 역순(4 → 3) 으로 스택에 추가
스택에서 3을 꺼내 출력 (더 이상 갈 곳 없음)
스택에서 4를 꺼내 출력 (더 이상 갈 곳 없음)
스택에서 2를 꺼내 출력하고, 이웃 노드 (5)를 스택에 추가
스택에서 5를 꺼내 출력 (탐색 종료)